基于新型纯积分法的定子磁链在线辨识算法

宋庆启, 苏文胜, 黄晓明, 曾 岑, 赵 羽, 岳前进

(1. 大连理工大学，辽宁 盘锦 124221；2. 江苏省特种设备安全监督检验研究院无锡分院，江苏 无锡 214174)

基于新型纯积分法的定子磁链在线辨识算法

宋庆启1, 苏文胜2, 黄晓明1, 曾 岑1, 赵 羽1, 岳前进1

(1. 大连理工大学，辽宁 盘锦 124221；2. 江苏省特种设备安全监督检验研究院无锡分院，江苏 无锡 214174)

针对气隙转矩法计算异步电机转矩时对定子磁链辨识精度的要求，提出了一种基于新型纯积分法的定子磁链在线辨识算法，采用了精度较高的复化辛普森积分模型。相比传统的梯形积分法，基于新型纯积方法的定子磁链在线辨识算法的磁链辨识精度显著提高；相比新型的基于低通滤波器的定子磁链观测器，该算法模型更简单，操作更便捷。通过MATLAB/Simulink搭建系统仿真平台进行验证，结果表明基于新型纯积分算法消除了传统积分法的主要缺陷，解决了积分饱和问题以及初值问题。基于新型纯积分算法的估计磁链与理论参考磁链基本吻合，表明其可靠性较高。

新型纯积分法;气隙转矩；定子磁链；在线辨识；复化辛普森法

0 引 言

随着能源短缺以及温室效应问题的日益严重，世界各国都把节约能源、开发新能源摆在国民经济发展的首要位置。在我国工业生产中，耗能最大的主要是机电产品，其中中小型三相交流异步电机的能耗约占2/3，总用电量占全国总电量的50%。目前工业中运行的电机大多都已经严重老化，效率降低，增加了额外的能耗，所以亟需开发一种便携式电机能效检测装置。传统的使用转速、转矩传感器的方法是不可取的，必须采用基于无传感器的转速、转矩辨识在线算法[1]。本文主要研究利用气隙转矩法计算电机转矩中最重要的定子磁链的在线辨识算法。

目前定子磁链在线辨识主要有3种方法：u-i模型，u-n模型和i-n模型。其中i-n模型依赖电机参数，而且需要准确的转速信息。u-n模型是u-i模型和i-n模型的综合，实现复杂，而且存在转换问题。u-i模型，即电压积分模型，其只需要定子电阻，对电机参数依赖小，是最简单的一种形式，但是其会产生两个严重的问题：一是采样电路的非对称性和非线性，会引起测量信号直流漂移，导致积分饱和；二是纯积分环节需要积分初值，在实际计算中，如果采用的初值不够精确，就会出现直流偏置。针对电压模型的主要缺陷，不同学者采用了不同的方法，主要分为闭环算法和开环算法两种。J. Hu等[2]提出了基于饱和反馈的闭环修改集成算法，成功地补偿了积分器直流偏置，但其准确性受限于饱和极限水平。文献[3-5]基于观测器的闭环定子磁链估计方案，提出了基于电流模型的全阶异步电机模型，它不同于前人的基于电压模型算法。C. Lascu等[6]提出了一种基于滑模非线性磁链观测器的定子磁链辨识技术，观测器动力学是基于滑模观测器动作而提高的，然而这个解决方案依赖于定子电流和定子磁链参考值，会导致静态误差。M. Barut等[7]提出了一个基于扩展卡尔曼滤波器的闭环磁链和转子速度的观测器。除了基于闭环的定子磁链估计，还有几个开环的解决方案，旨在克服纯积分法估计定子磁链的缺点。其一般为基于低通滤波器而不是纯积分器。文献[8-10]中作者提出了一种改进的低通滤波器算法，用一阶低通滤波器代替纯积分算法，此方法能有效抑制直流偏置，但是调节合适的截止频率比较困难，过大或过小的截止频率都会影响观测器的性能指标。何志明等[11]和Djordje Stojic等[12]分别对低通滤波器算法进行改进，交换幅值、相位补偿模块和低通滤波模块的顺序，来提高定子磁链观测的动态性能。在文献[13]中，提出了可编程级联低通滤波器，可以解决零漂的影响，但是对截止频率的控制要求高。李红等[14]提出了一种带通滤波器算法，该方法解决了直流偏置以及积分初值问题，但是存在明显误差。王庆等[15]采用传统的积分法来求解定子磁链，解决了积分初值问题，但是没有解决电压、电流零漂问题，而且，文中使用的梯形法虽然简单，但误差较大。

传统的积分法没有考虑电压、电流零漂以及磁链初值问题，新型积分器结构复杂，需要的电机参数更多，而且有些参数在现场很难获得，根据低通滤波器改进的算法对截止频率的控制要求特别高，不合适的截止频率都会影响观测器性能指标。

本文提出了一种新型的基于纯积分法的异步电机定子磁链在线辨识算法，采用精度较高的辛普森积分算法代替简单的梯形法，仿真精度高。该方法结构简单，容易实现，解决了其他算法的缺陷，本文通过MATLAB/Simulink进行仿真，结果表明了该算法的可靠性。

1 电压积分型定子磁链观测器分析

由于现场检测时没有转矩传感器，所以采用基于气隙转矩的电机输出转矩辨识算法。由电机学可知，三相电压可以表示为

所以，电机磁链在三相静止坐标系下的表达式为

为了简化计算，提高定子磁链辨识精度，将三相电压、电流信号进行Clark变换，得到定子磁链在两相静止坐标系下的表达式为

式中：ψsα、ψsβ、usα、usβ、isα、isβ——定子磁链、相电压、相电流在α轴和β轴上的分量。

考虑到通过传感器采集的电压、电流信号均是离散的，需要对定子磁链计算公式进行离散化，由式(3)可得电压积分模型的离散表达式[14]

ψsα(k)=ψsα(k-1)+T[usα(k)-risα(k)]=

…

式中：T——电压、电流信号的采样周期；

usα(i)、isα(i)——i时刻电压、电流的瞬时值(i=1，…，k)；

r——定子电阻；

ψsα0——初始状态时定子磁链在α轴的分量,ψsα(0)=ψsα0，同理，在β轴上的表达式与α轴一样。

由式(4)可知，影响定子磁链观测的因素有电压电流值、磁链初值。下面分析这两类因素对磁链观测的影响。

电压电流通过采样电路获得，但采样电路不具备理想的对称性和线性，采样结果出现零漂。假设usα、isα的零漂分别为Δusα、Δisα，分别代入式(4)可得：

由式(5)可看出，k每增加一次，零漂值就累加一次，ψsα(k)的幅值会越来越大，最终超出寄存器数值范围，达到积分饱和[14]。

同样，由式(4)可知，ψsα0会造成ψsα(k)整体偏移，造成直流偏置。综上所述，传统积分法由于电压电流零漂和磁链积分初值的问题而存在明显的缺陷。本文主要解决这两种缺陷，使定子磁链的辨识精度提高。

2 新型纯积分法定子磁链辨识算法设计

王庆等[15]针对气隙转矩中磁链的求解采用了简单的梯形法，根据气隙转矩公式，需要求取两相绕组的磁链差，由于实时计算气隙转矩计算量很大，所以采用了分别计算各采样周期磁链差增量的方法解决，从而减少了计算量。另外，由于磁链差增量Δφ与磁链差φ的相位相差π/2，当Δφ达到最小值时，对应的磁链差φ的值为零，从而可以找到φ=0的时刻，便可以利用每一时刻的增量Δφ得到任意时刻的磁链差值φ。但是梯形法采用直线拟合方式，积分误差较大。本文采用辛普森法实现定子磁链的计算，相比梯形法提高了积分精度，转矩的辨识精度提高。为了解决转矩辨识实时性问题，本文采用复化辛普森法进行计算。

辛普森公式是利用区间二等分的3个坐标点进行积分插值，采用二次抛物线近似代替原积分曲线，能解决不同曲线线型或直线上的坐标计算问题。在纵坐标数目相同的情况下，辛普森法的计算误差明显小于梯形法。在实际应用中，将曲线分为n个子区间，分别计算各子区间的积分值，然后相加，得到最后结果，称为复化辛普森法。

假设定子电压、电流的采样周期为T，令f(k)=usα-risα，则在lT～(l+2)T区间上的辛普森积分公式为

依次求得相邻两个周期的定子磁链增量，并依次组合相加即可求得任意时刻的定子磁链值，从而实现了定子磁链的在线辨识。

2.1消除电压、电流零漂影响

一般情况下，在已知的采样电路下，电压、电流的零漂是固定的，即

式中：usα、isα——电压、电流测量值；

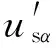
Δusα、Δisα——电压、电流零漂。

当采样的电压、电流出现零漂后，只是相对于原始平衡位置上下平移了一个零漂值，所以根据正弦信号的特性，只需检测出电压、电流的峰值，电压、电流峰值和谷值之和的一半即为当前信号的平衡位置，进而可以计算出零漂值，从而将电压、电流还原到真实情况，解决了积分饱和问题。

2.2解决积分初值问题

对于给定的采样数据，采样点的初始时刻t0是确定的，从而定子磁链的初值ψsα0也是确定的。假设t0时刻的积分初值已知，则后续计算的每一时刻的磁链变化曲线是一种标准的正弦波形，平衡位置为零。然而，如果设定t0时刻的积分初值为零，则后续得到的每一时刻的磁链波形图会相对原始平衡位置偏置一个值，这个值即积分初值。因此，电压、电流零漂和积分初值问题相似，实际是目标信号的直流偏置问题。检测出目标信号的峰值，然后计算其偏置量，即可还原原始信号，从而提高定子磁链辨识精度。

2.3消除偏置问题

根据2.1和2.2的分析可知，电压、电流的零漂和定子磁链的初值问题都可以归纳为目标信号的直流偏置问题。当一个信号相对原始位置发生偏置时，信号上的每一个点都会增加一个偏置量，因此，目标信号只是更换了平衡位置，各信号点的相对位置不会发生改变，故目标信号的偏置问题转变成了求解新的平衡位置。为了找到目标信号的平衡位置，只需要搜索到信号一个周期内的最大值、最小值即可，偏置量即为二者之和的一半，偏置问题即可消除。

3 仿真验证

为了验证本文所提出的新型定子磁链辨识算法，建立了基于MATLAB/Simulink的异步电机仿真模型。仿真模型中采用的电机参数如表1所示，仿真模型见图1。

表1 仿真电机参数

图1 新型算法仿真模型

图2 消除电压零漂

图3 消除电流零漂

首先验证新型定子磁链在线辨识算法对电压、电流的零漂产生的直流偏置的消除效果。由于Simulink仿真模型中测量的电机电压、电流并没有发生零漂，故在此对电压、电流分别加入随机产生的零漂。然后采用基于波形峰值检测的偏置消除方法对产生零漂的电压、电流进行复原，仿真结果如图2、图3所示。从图2、图3可以看出，该算法成功检测出随机添加的零漂值，电压为+50 V，电流为+1 A，经过处理后的电压、电流波形恢复正常，在0点上下均匀波动。该方法很好地消除了定子电压、电流的零漂，从而解决了传统纯积分法的积分饱和问题。

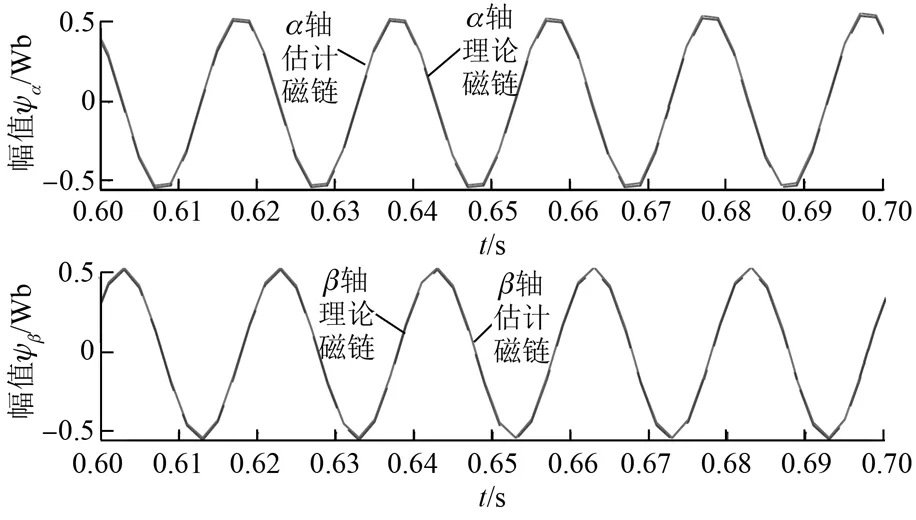
图4 新型磁链辨识算法仿真结果

新型磁链辨识算法的仿真结果如图4所示，其中，α轴和β轴的理论磁链是在Simulink仿真模型中，通过电机测量模块直接测量得出的电机运行时真实的磁链值，在图4中用实线表示。α轴和β轴的估计磁链是通过本文中提出的新型定子磁链辨识算法计算的磁链，在图4中用虚线表示。

从图4中可以看出，在α轴和β轴上，无论是磁链的幅值还是相位，理论磁链和估计磁链几乎完全重合。从局部放大图图5中可以看出，两者的误差很小，达到10-3量级，这也反映了本算法的精度范围。这一定子磁链估计算法可以用于后续气隙转矩的计算，由此带来的误差将会很低。

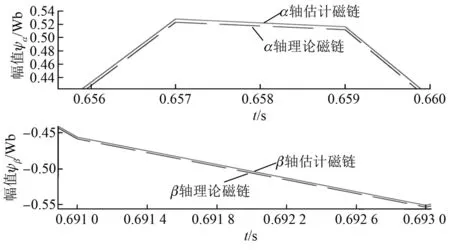
图5 新型磁链辨识算法仿真结果的局部放大图

图6 新算法与传统积分法结果对比

为了说明本文提出的新型定子磁链辨识算法的精度问题，我们与文献[15]中所提出的梯形法进行对比，其仿真结果如图6所示。本文提出的新型定子磁链辨识算法和传统积分法的辨识误差对比如图7所示。由于传统积分法没有解决电压、电流零漂问题，从而造成了较大的辨识误差，误差在-0.1～-0.18之间波动。本文提出的新型算法由于解决了传统积分法存在的电压、电流零漂及定子磁链初值问题的缺陷，所以其辨识精度很高，误差稳定在-0.002 5左右。

图7 新算法与传统积分法(含零漂)误差比较

假如消除电压、电流零漂对梯形法的影响，两种方法的误差对比如图8所示。由图8可以看出，梯形法即使消除零漂的影响，其辨识误差也达到了0.004～-0.006。对比这两种方法的辨识误差可以看出，本文的方法不仅误差幅值明显小于文献[15]的梯形法，而且波动也比梯形法小得多。这从侧面反映出本文提出的新算法的精度与可靠性优于前人，为传统积分法求解定子磁链指明了一条道路。

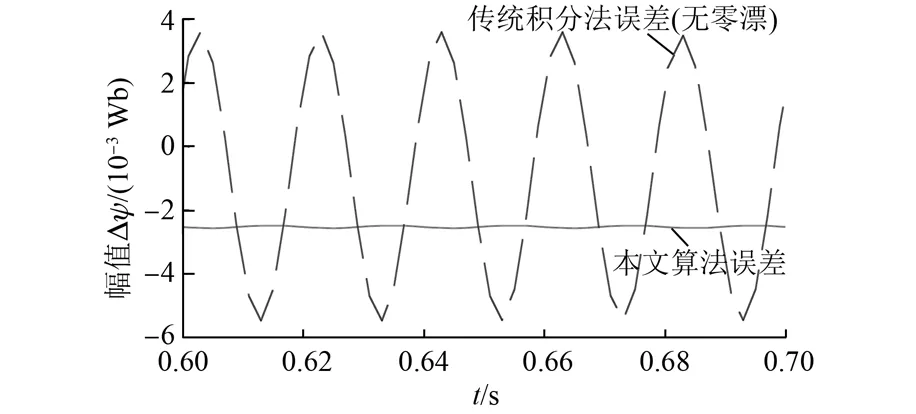
图8 新算法与传统积分法(无零漂)误差比较

4 结 语

本文提出了一种基于纯积分法的新型定子磁链在线辨识算法，并运用MATLAB/Simulink进行仿真，仿真结果达到了预期的目的，即解决了定子磁链初始相位问题以及消除电压、电流的零漂而导致的积分饱和问题。定子磁链的仿真波形与理论波形一致，相比传统的梯形积分法精度更高，在线辨识误差更小，有助于减小电机气隙转矩的波动，提高转矩的计算精度。本文提出的基于纯积分法的新型定子磁链在线辨识算法适用于现场中小型异步电机的能效检测中，用于气隙转矩中定子磁链的估计，具有很深远的现实意义与应用价值。

[1] 韦锋,孙逊,史伟伟.便携式电机能效检测仪的研制[J].机电信息,2012(3): 125-129.

[2] HU J, WU B. New integration algorithms for estimating motor flux over a wide speed range[J].IEEE Trans Power Electron,1998,13(5): 969-977.

[3] HINKKANEN M. Analysis and design of full-order flux observers for sensorless induction motors[J].IEEE Trans Ind Electron,2004,51(5): 1033-1040.

[4] KOWALSKA T O, DYBKOWSKI M. Stator-current-based MRAS estimator for a wide range speed-sensorless induction-motor drive[J].IEEE Trans Ind Electron,2010,57(4): 1296-1308.

[5] MAES J, MELKEBEEK J A. Speed-sensorless direct torque control of induction motors using an adaptive flux observer[J].IEEE Trans Ind Appl,2000,36(3): 778-785.

[6] LASCU C, ANDREESCU G D. Sliding-mode observer and improved integrator with DC-offset compensation for flux estimation in sensorless controlled induction motors[J].IEEE Trans Ind Electron,2006,53(5): 785-791.

[7] BARUT M, BOGOSYAN S, GOKASAN M. Speed-sensorless estimation for induction motors using extended Kalman filters[J].IEEE Trans Ind Electron,2007,54(5): 272-280.

[8] LI Y, HUANG W X, HU Y W. A low cost implementation of stator-flux-oriented induction motor drive[C]∥Proceedings of the Eighth International Conference on Electrical Machines and Systems,2005: 1534-1538.

[9] 万宇宾,胡婵娟,万淑芸.基于电压模型的定子磁链观测器及参数设计方法[J].电气传动,2006,36(3): 15-18.

[10] 黄志武,李艺,单勇腾,等.一种新型的改进型积分器定子磁链观测器[J].计算机仿真,2007,24(5): 329-333.

[11] 何志明,廖勇,向大为.定子磁链观测器低通滤波器的改进[J].中国电机工程学报,2008,28(18): 61-65.

[12] STOJIC D, MILINKOVIC M, VEINOVIC S. Improved stator flux estimator for speed sensorless induction motor drives[J].IEEE Transactions on Power Electronics,2015,30(4): 2363-2371.

[13] BOSE B K, PATEL N R. A programmable cascaded low pass filter-based flux synthesis for a stator flux-oriented vector-controlled induction motor drive[J].IEEE Transactions on Industrial Electronics,1997,44(1): 140-143.

[14] 李红,罗裕,韩邦成,等.带通滤波器法电压积分型定子磁链观测器[J].电机与控制学报,2013,17(9): 8-16.

[15] 王庆,张蓬鹤,赵海森,等.基于可测电气量鼠笼式异步电机能效在线监测方法[J].微特电机,2013,41(12): 26-30.

ResearchonOnlineIdentificationAlgorithmofStatorFluxBasedonNewPureIntegralMethod

SONGQingqi1,SUWensheng2,HUANGXiaoming1,ZENGCen1,ZHAOYu1,YUEQianjin1

(1. Dalian University of Technology, Panjin 124221, China;2. Wuxi Branch of Jiangsu Province Special Equipment Safety Supervision Inspection Institute, Wuxi 214174, China)

In order to fulfill the requirement of stator flux identification accuracy in the calculation of air-gap torque, puts forward a stator flux online identification algorithm based on a new pure integral method, which used mulriple simpson integral model. Compared with the traditional trapezoidal integral method, this model improved the identification precision of the stator flux; while compared with the new stator flux observer based on low-pass filter, it was more simple and easy to operate and implement. Through MATLAB/Simulink platform, a simulation system was built. The results showed that the algorithm eliminate the major drawbacks of traditional integration method and solve the integral saturation and initial value problems. The stator flux estimated used the new algorithm essentially coincident with the theoretical results, showed the higher reliability of the algorithm.

newpureintegralmethod;air-gaptorque;statorflux;onlineidentification;mulriplesimpsonmethod

宋庆启(1990—)，男，硕士研究生，研究方向为机电装备研发。

TM 343

A

1673-6540(2017)10- 0088- 06

2016 -12 -20

[期刊简介]

《电机与控制应用》(原《中小型电机》)创刊于1959年，是经国家新闻出版总署批准注册，由上海电器科学研究所(集团)有限公司主办的具有专业权威的电工技术类科技期刊。

期刊定位于电机、控制和应用三大板块，以中小型电机为基础，拓展新型的高效节能和微特电机技术，以新能源技术和智能控制技术引领和提升传统的电机制造技术为方向，以电机系统节能为目标开拓电机相关应用，全面报道国内外的最新技术、产品研发、检测、标准及相关的行业信息。

本刊每月10日出版，国内外公开发行，邮发代号4-199。在半个多世纪的岁月中，该杂志为我国中小型电机行业的技术进步与发展做出了巨大的贡献，在中国电机及其应用领域享有很高的影响。

依托集团公司雄厚的技术实力和广泛的行业资源，《电机与控制应用》正朝着专业化品牌媒体的方向不断开拓创新，在全国科技期刊界拥有广泛的知名度，是“中国学术期刊综合评价数据库来源期刊”、“中国科学引文数据库来源期刊”、“中国学术期刊(光盘版)全文收录期刊” ，得到了业内人士的普遍认可，备受广大读者的推崇和信赖，多次被评为中文核心期刊、中国科技核心期刊、全国优秀科技期刊。