基于Lyapunov函数的永磁同步电机速度控制器设计*
王 杰, 谢 源, 肖立健, 金鹏飞
(上海电机学院 电气学院,上海 201306)
基于Lyapunov函数的永磁同步电机速度控制器设计*
王 杰, 谢 源, 肖立健, 金鹏飞
(上海电机学院 电气学院,上海 201306)
传统的PI 速度控制器具有速度超调、动态时间长、跟踪精度低、抗负载转矩扰动能力和恢复能力差等缺点。提出了利用永磁同步电机(PMSM)的运动方程和转矩方程推导出控制系统q轴电流给定量,基于Lyapunov稳定性条件设计出的一种PMSM速度控制器。相比于传统的PI速度控制器,该控制器没有速度超调量、动态时间短、跟踪精度高,抗负载扰动能力和恢复能力有一定的提高。利用 MATLAB/Simulink仿真软件,搭建控制系统模型并进行仿真分析。仿真验证了提出的PMSM速度控制器的有效性,获得了很好的速度控制性能。
永磁同步电机;速度控制器;Lyapunov函数
0 引 言
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM) 相对异步电机具有结构简单、体积小、重量轻、转动惯量小、高效率和控制性能好等优点,大量应用于工业生产、日常生活、航空航天、军事设施等领域,具有非常诱人的前景。PMSM更加适用于高精度的伺服控制系统。这些领域对PMSM的控制系统有很高的要求,因此研究PMSM的控制系统具有重要的意义。
PMSM的控制系统存在模型不精确、参数时变、负载扰动、电机本身的非线性、强耦合等特性,因此对相应的控制策略有很高的要求。文献[1-3]指出,传统的PI控制算法,由于具有速度超调、动态时间长、跟踪精度低和抗负载转矩扰动恢复能力差等缺点,并不能很好地满足某些控制领域控制要求高的需求。随着现代控制理论和智能控制算法的不断深入研究,一些先进的控制策略已经用于PMSM的速度控制,并取得了不错的效果,但也有一些缺点。例如文献[4-7]提出的自适应控制,通过不断的改变参数增益使控制性能更好,但需要实时计算,计算量大。文献[8-10]中的滑模变结构控制,具有很强的鲁棒性,但抖振问题难以解决。文献[11-13]提出的神经网络控制,能够精确地控制速度,控制性能优越,但神经网络计算量大,需要不断地学习和训练。还有文献[14-17]中提到的模糊控制,由于模糊库难以准确建立,控制效果有待验证。以上这些控制策略从不同方面提高了PMSM速度的控制精度,在一定程度上满足了控制系统的实际要求,但上述的控制策略对系统模型的要求相对较高、算法复杂,有些控制策略存在着积分直流偏置等缺点,影响了其控制性能。同时还需要高性能的微型处理器才能满足伺服控制系统实时性的要求,增加了系统的设计成本。
本文提出了一种基于Lyapunov函数的PMSM速度控制器。它是利用PMSM的运动方程和转矩方程推导出控制系统q轴电流给定量,根据Lyapunov稳定性条件,设计的一种速度控制器。相比于传统的PI速度控制器,该控制器没有超调量、动态时间短、跟踪精度高,抗负载扰动能力和恢复能力有明显的提高。
1 PMSM的数学模型及控制策略
以表贴式永磁同步电机(Surface Permanent Magnet Synchronous Motor,SPMSM)为研究对象(直轴和交轴电感相等,即Ld=Lq=Ls),采用文献[13]中的PMSM的dq轴数学模型满足以下条件:(1)忽略电动机铁心饱和;(2)不计磁滞和涡流损耗;(3)转子上没有阻尼绕组,永磁体也没有阻尼作用;(4)绕组中感应电动势是正弦波。
PMSM的dq轴数学模型如下。
定子电压方程:
定子磁链方程:
将式(2)代入到式(1),可得定子电压方程:
电磁转矩方程:
式(4)是针对内置式三相PMSM建立的数学模型;对于表贴式三相的SPMSM而言,定子电感满足Ld=Lq=Ls。因此表贴式三相的SPMSM电磁转矩方程:
机械运动方程:
式中:ud、uq——定子电压的d、q轴分量;
id、iq——定子电流的d、q轴分量;
R——定子的电阻;
φd、φq——定子磁链的d、q轴分量;
ωe——电角速度;
ωm——机械角速度;
Ld、Lq——定子d、q电感分量;
Ls——定子电感;
φf——永磁体磁链;
p——极对数;
J——转动惯量;
Te——电磁转矩;
TL——负载转矩;
B——阻力系数。
采用文献[18-20]提出的id=0的控制策略,在id=0控制中,定子电流中只有交轴分量,直轴电流由于给定值为0使之维持在0附近,相当于直轴绕组开路。定子的磁动势在空间上就与永磁体的磁场正交,PMSM相当于直流电机。因此,只需要控制交轴转矩电流就可以控制其输出转矩和速度。这种控制方法具有控制系统简单、控制灵活、转矩性能好等特点,而且调速范围比较宽,在要求具有高性能、宽调速范围的应用场合得到很好的应用,尤其在数控机床及机器人等领域得到了广泛应用。
2 传统PI速度控制器
2.1PI速度控制器分析
由文献[21]知,根据图1所示,假设实际电流实时完全的跟随给定电流,则Gi(s)=1。

图1 id=0控制系统框图(PI控制器)
由图1可以得到传统PI速度控制系统的两个传递函数:
由式(7)、式(8)可知,由于GT(s)、Gω(s)不能独立设计,负载转矩变化时,速度必然存在波动。从式(8)明显能看到,控制器在控制电机速度时,由于传递函数分子中存在较大的微分项,当速度为给定的阶跃信号时,则会存在较大的速度超调和q轴冲击电流。这也是传统PI控制器固有的缺点。
2.2基于Lyapunov函数的速度控制器设计

PMSM调速系统的主要作用是实际速度实时跟踪给定速度,同时当转矩发生突变时能快速的稳定转矩并恢复到给定速度,所以其控制目标主要是速度跟踪,具体设计如下。
定义跟踪误差为
选择e为系统的状态变量,构成与e相关的子系统。其子系统方程为
为了使系统速度跟踪误差趋向于零,对于子系统式(10),构造合适的Lyapunov函数如下:
对式(11)进行求导得
将式(5)代入到式(12)中得
从式(14)可以求出系统q轴电流给定值:
根据式(15)便可以设计速度控制器。该速度控制器具有计算简单,收敛速度快,无超调和跟踪精度高等优点。图2是该速度控制器仿真内部结构图。通过该速度控制器能够很好地调节电机转速。

图2 基于Lyapunov函数的速度控制器仿真模块
3 系统仿真与分析
采用id=0的矢量控制策略,速度控制器采用基于Lyapunov函数的速度控制器,电流控制器是传统PI控制器,选取电机为MATLAB/Simulink中自带的PMSM。其控制结构框图如图3,电机参数如表1所示。

图3 系统结构控制框图

参数名称参数值定子电阻R/Ω0.331定子电感L/H0.0021永磁体磁通φf/Wb0.3537转动惯量J/(kg·m2)0.0008粘滞摩擦因数B0.001极对数p4
为了验证该速度控制器的有效性和优越性,本文在MATLAB/Simulink软件环境下搭建了系统仿真模型,设置速度n=1 000 r/min,仿真时间0.2 s。分别在传统的PI速度控制器和本文设计的速度控制器系统下进行仿真,仿真结果如图4、图5所示。
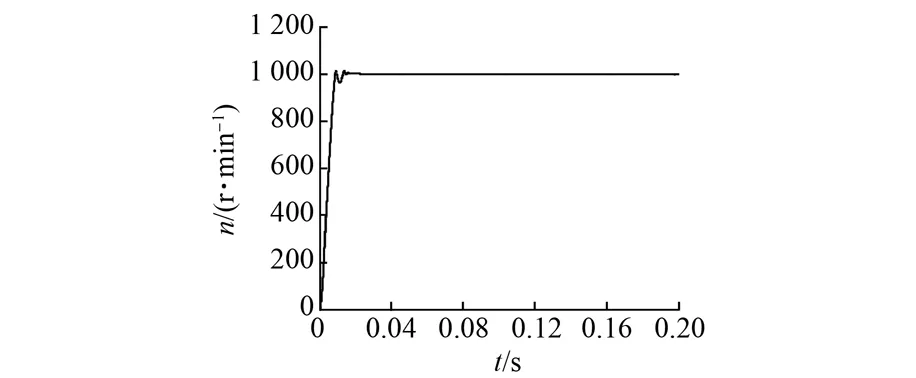
图4 传统PI速度控制器的波形

图5 基于Lyapunov函数的速度控制器的波形
对比图4和图5,明显可以看到传统PI速度控制器约有2%的超调量,而基于Lyapunov函数的速度控制器没有超调量。这对于整个电机硬件的要求就会适当降低,减少电机硬件的损坏。在图中可以看出,它们的动态响应时间也是不相同的,图4中传统的PI控制,动态响应时间约0.017 s,之后系统便处于稳定状态。图5中系统动态响应时间约为0.01 s,响应时间大约缩短了70%,说明该速度控制器能有效的缩短动态响应时间。
为了验证两个速度控制器的跟踪精度、抗负载扰动能力和负载扰动后的恢复能力,做如下试验:设置n=1 000 r/min,电机在初始负载转矩为0 N·m,0.1 s后负载转矩为2 N·m。仿真结果如图6、图7所示。

图6 传统PI控制器负载扰动波形
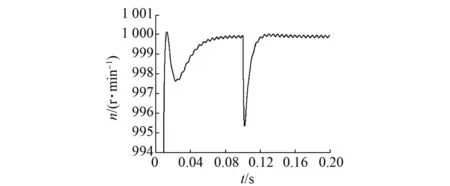
图7 基于Lyapunov函数的速度控制器负载扰动波形
转速跟踪精度方面分析,从图6可知,传统的PI速度控制器作用下的系统初始速度稳定在998.7 r/min,与给定速度1 000 r/min的误差是1.3 r/min,误差率0.13%;当t=0.1 s时负载转矩突变后,系统速度稳定在998.2 r/min,速度跟踪误差是1.8 r/min,误差率0.18%。从图7可知,基于Lyapunov函数的速度控制器作用下的系统初始速度稳定在999.8 r/min,与给定速度1 000 r/min的误差是0.2 r/min,误差率0.02%;当t=0.1 s负载转矩突变时,系统速度依然稳定在999.8 r/min,误差率依然是0.02%。可见在速度跟踪精度方面,基于Lyapunov函数的速度控制器有很好的效果。
抗负载扰动能力和负载扰动后的恢复能力方面分析,传统PI速度控制器因有积分器的存在,故对负载的扰动有较好的效果。但从图6可知,PI速度控制器的初始负载转矩为0 N·m时,速度稳定值约为998.7 r/min;当0.1 s时负载突加至2 N·m时,速度波动后,稳定在约998.2 r/min,可见,负载扰动后传统PI控制器不能恢复到原来的稳定值附近。由图7可知,相对于图6抗负载扰动上稍差一些,但从系统扰动后恢复能力看,基于Lyapunov函数的速度控制器具有明显的优势,从图7可知,当初始负载转矩为0 N·m时,速度稳定值约在999.8 r/min;当0.1 s负载突加至2 N·m时,系统稳定后速度依然稳定在约999.8 r/min,可见该速度控制器的恢复能力较强,不会出现传统PI速度控制器因负载扰动而出现速度断层的现象。综上分析可知,基于Lyapunov函数的速度控制器相比于传统的PI控制器在速度跟踪精度和负载扰动恢复能力方面具有较为明显的优势。
由于基于Lyapunov函数的速度控制器的控制性能优越、控制精度高,所以在负载转矩突变时刻的转矩波动也有明显的减少。为了验证这个观点,做如下仿真:使用上个仿真试验的数据,n=1 000 r/min,电机在初始负载转矩为0 N·m,0.1 s后负载转矩为2 N·m,仿真结果如图8、图9所示。

图8 传统PI速度控制器控制下的转矩
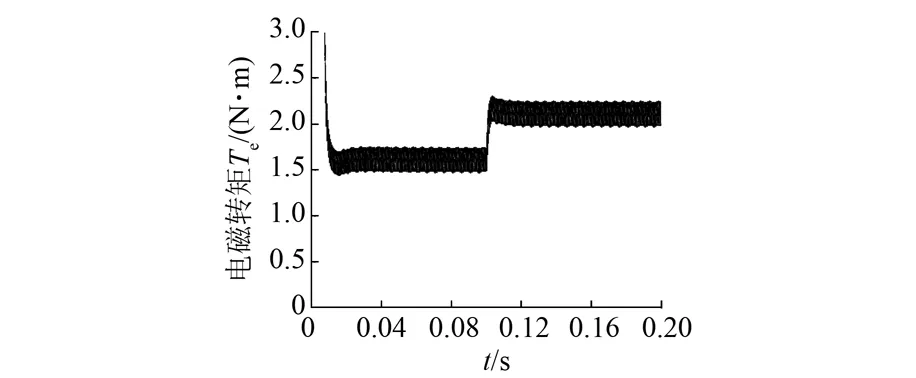
图9 基于Lyapunov函数的速度控制器下的转矩
图8中显示电机在初始起动过程中转矩脉动很大,在t=0.1 s负载突变时也出现了较大的脉动。相比较于图9,在电机初始起动过程中转矩脉动很小,同时在t=0.1 s负载突变时几乎没有脉动,响应平稳。由此可知,基于Lyapunov函数的速度控制器对于负载转矩突变带来的转矩脉动能够起到很好的抑制作用。
4 结 语
基于Lyapunov函数的速度控制器无超调量、动态时间短、速度跟踪精度较高、抗负载突变恢复能力强,同时,对于电磁转矩有很好的优化能力,能够很好地抑制在起动和负载转矩突变过程中带来的转矩脉动的影响。
仿真结果表明,相比于传统的PI速度控制器,基于Lyapunov函数的速度控制器使系统动态响应时间从0.017 s缩短到0.01 s,提高了70%;速度跟踪误差从1.3 r/min缩小到0.2 r/min,提高了约6倍,速度跟踪精度有了很大的提高。仿真试验表明该速度控制器具有很好的抗负载转矩扰动恢复能力,能很好地恢复到之前的速度;同时,能够优化电磁转矩,对于因负载转矩突变引起的转矩脉动有很好的抑制效果。
[1] 齐亮,贾廷纲,侍洪波.永磁同步电机Anti-Windup速度控制器设计[J].电机与控制应用,2011,38(9): 17-20.
[2] 符慧,左月飞,刘闯,等.永磁同步电机速度环的一种变结构PI控制器[J].电工技术学报,2015,30(12): 237-242.
[3] 周华伟,温旭辉,赵峰,等.一种具有预测功能的抗积分饱和PI速度控制器[J].电机与控制学报,2012,16(3): 15-21.
[4] 史敬灼,张慧敏.行波超声波电机Lyapunov模型参考自适应速度控制[J].电工技术学报,2011,26(4): 44-50.
[5] ZHAO Y, QIAO W, WU L. Model reference adaptive system-based speed estimators for sensorless control of interior permanent magnet synchronous machines[C]∥ Transportation Electrification Conference and Expo (ITEC),2013: 1-6.
[6] 邓艳艳,林旭梅.永磁同步电机滑模自适应控制[J].计算机仿真,2015,32(2): 337-341.
[7] JAKUB B, JAKUB K, SLAWOMIR S, et al. Adaptive control of permanent magnet synchronous motor with constrained reference current exploiting backstepping methodology[C]∥ IEEE Conference on Control Applications (CCA),2014: 1545-1550.
[8] 佘致廷,董旺华,秦亚胜,等.基于反步滑模变结构的PMSM速度控制[J].控制工程,2016,23(增刊): 1-5.
[9] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3): 407-418.
[10] 刘颖,周波,方斯琛.基于新型扰动观测器的永磁同步电机滑模控制[J].中国电机工程学报,2010,30(9): 80-85.
[11] 刘瑛,程善美.基于神经网络的新型复合速度控制器的设计[J].控制工程,2005,12(2): 135-137.
[12] 佘致廷,卢文斗,谭琼琼,等.PMSM神经网络模型参考自适应的速度控制[J].控制工程,2015,22(增刊): 29-34.
[13] LI L, GU Z P, TIAN J F. Neural network-sliding mode control of permanent magnet synchronous linear motor[C]∥ Chinese Control and Decision Conference (CCDC),2016: 3061-3064.
[14] 方一鸣,于晓,牛犇,等.永磁同步电机的自适应模糊终端滑模速度控制[J].中南大学学报,2013,44(12): 4855-4860.
[15] KAVEH M, JAFAR M M. A genetic based fuzzy logic controller fordirect torque controlled IPMSM drives over wide speed range[C]∥ 2007 IEEE International Electric Machines and Drives Conference,2007: 847-853.
[16] 张碧陶,皮佑国.基于模糊分数阶滑模控制的永磁同步电机控制[J].华南理工大学学报,2012,40(3): 126-130.
[17] 王晓远,田亮,冯华.无刷直流电机直接转矩模糊控制研究[J].中国电机工程学报,2006,26(15): 134-138.
[18] 丁文,高琳,梁得亮,等.永磁同步电机矢量控制系统的建模与仿真[J].微电机,2010,43(12): 66-71.
[19] BARBARA B, GIANMARIO P. Model-based directflux vector control of permanent magnet synchronous motor drives[J]. IEEE Transactions on Industry Applications,2015,51(4): 3126-3136.
[20] 朱军,程志磊,汪旭东,等.一种永磁同步电机电流直接反馈矢量控制[J].电机与控制学报,2015,19(6): 35-39.
[21] 郭新华,温旭辉,赵峰,等.基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器[J].中国电机工程学报,2010,30(27): 7-13.
DesignofPermanentMagnetSynchronousMotorSpeedControllerBasedonLyapunovFunction*
WANGJie,XIEYuan,XIAOLijian,JINPengfei
(College of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)
The traditional PI speed controller of has the disadvantages of speed overshoot, long dynamic time, low tracking precision, poor ability of load torque disturbance and recovery. A speed controller was proposed. It was based on the motion equation and the torque equation of the permanent magnet synchronous motor to derive theqaxis current of the control system. A speed controller of permanent magnet synchronous motor was designed according to the Lyapunov stability condition. Compared with the traditional PI speed controller, the controller had no speed overshoot, short dynamic time and high tracking precision, and improved ability of load torque disturbance and recovery. By using MATLAB/Simulink simulation software, the control system model was built and the simulation analysis was carried out. Simulation results showed that the speed controller of PMSM was effective, and it could get a good speed control performance.
permanentmagnetsynchronousmotor(PMSM);speedcontroller;Lyapunovfunction
国家自然科学基金项目(61374136,11304200);上海市自然科学基金项目(14ZR1417200)
王 杰(1990—)男,硕士研究生,研究方向为电机驱动与控制。
TM 301.2
A
1673-6540(2017)10- 0030- 06
2017 -03 -06

