基于混合控制集预测控制的永磁同步电机电流脉动抑制方法*
程 坦, 苏宗昱, 郑 伟, 牛建平
(1. 国网辽宁省电力有限本溪供电公司,辽宁 本溪 117000;2. 沈阳大学 电气工程学院,辽宁 沈阳 110000)
基于混合控制集预测控制的永磁同步电机电流脉动抑制方法*
程 坦1, 苏宗昱1, 郑 伟1, 牛建平2
(1. 国网辽宁省电力有限本溪供电公司,辽宁 本溪 117000;2. 沈阳大学 电气工程学院,辽宁 沈阳 110000)
模型预测控制(MPC)技术近年来在高动态性能电机驱动系统中应用广泛。为了克服传统MPC技术中有限控制集(FCS)造成的稳态电流脉动问题,提出了一种基于混合控制集(MCS)预测控制的永磁同步电机(PMSM)电流脉动抑制方法。分析建立PMSM预测控制系统离散数学模型,并分析电压矢量精度与电流脉动之间的关联性;在此基础上,MCS-MPC将电压源型逆变器有限的有效电压矢量数,扩展为多个以占空比形式存在的虚拟电压矢量,并基于上述虚拟电压矢量完成MPC优化问题在线求解;此外,考虑到MCS-MPC系统的参数敏感性问题,对MCS-MPC系统反馈噪声问题进行分析讨论。最后,搭建双15 kW PMSM对拖样机测试平台进行试验分析,分析内容包括MCS方法动态跟踪特性、电流脉动稳态效果。试验结果表明所提出的MCS-MPC方法在保留了传统预测控制技术高动态响应的基础上,可有效降低PMSM稳态电流脉动幅度和运行噪声。
永磁同步电机;模型预测控制;混合控制集;电流脉动抑制
0 引 言
伴随着现代工业中以工业机器人[1]、3D打印[2]、智能制造[3]等为代表的高精度伺服驱动的不断发展,整机系统对电力驱动环节转矩响应速度提出了愈加严苛的要求[4-5]。此时,传统线性PI控制器已经无法满足高带宽条件下的电机转矩高性能响应需求,模型预测控制[6-8](Model Predictive Control,MPC)技术正是在上述背景下被提出,并在高性能电机驱动系统中取得成功应用,经过多年发展,MPC技术逐步演变为广义预测控制[6](Generalized Predictive Control,GPC)、显式预测控制[7](Explicit MPC,EMPC)以及有限控制集预测控制[8](Finite Control Set MPC,FCS-MPC)等。在上述方法中,FCS-MPC[8-10]考虑了电力电子逆变器有限的电压矢量状态,可以在电机驱动系统ms级的采样周期内完成包括:模型预测、滚动优化以及脉冲输出等多个步骤运算,有效降低了传统GPC、EMPC方法的运算维度,使得MPC思想可以在现有数字处理系统中有效执行。但是,考虑到逆变器可输出基本电压矢量的有限性,文献[11]中指出FCS-MPC方法较之现有矢量控制系统稳态精度较差,具体表现在电流纹波及其谐波分布规律上。
为了克服传统FCS-MPC存在的稳态电流脉动问题,本文提出了一种基于混合控制集(Mixing Control Set,MCS)预测控制的PMSM电流脉动抑制方法。首先,分析建立PMSM预测控制系统离散数学模型,并分析电压矢量精度与电流脉动之间的关联性;在此基础上,MCS-MPC将电压源型逆变器有限的有效电压矢量数,扩展为多个以占空比形式存在的虚拟电压矢量,并基于上述虚拟电压矢量完成MPC优化问题在线求解;此外,考虑到MCS-MPC系统的参数敏感性问题,对MCS-MPC系统反馈噪声问题进行分析讨论。最后,搭建双15 kW PMSM对拖样机测试平台进行试验分析,分析内容包括MCS方法动态跟踪特性、电流脉动稳态效果。试验结果表明所提出的MCS-MPC方法在保留了传统预测控制技术高动态响应的基础上,可有效降低PMSM稳态电流脉动幅度和运行噪声。
1 永磁伺服驱动系统FCS-MPC原理
图1所示为高精度永磁伺服驱动系统结构示意图,其中逆变器采取三相全桥式两电平拓扑,abc三相开关器件分别为S1、S2、S3、S4、S5、S6,直流母线电压为Udc。令图1中PMSM-VSI调速系统为三相理想对称结构,建立两相旋转dq坐标系下的系统数学模型如下:
式中:Ud、Uq——dq轴定子电压;
id、iq——dq轴定子电流;
Rs——定子电阻;
Ld、Lq——dq轴电感;
Ψm——永磁体磁链值;
ωr——转子旋转角速度。

图1 高精度永磁伺服驱动系统结构示意图
当数字处理系统的控制频率fc足够高时,可认为各变量在一个控制周期Tc内基本保持不变。此时,采取欧拉公式可将式(1)中微分方程等效为
式中: d/dt——微分算子;
上标k、k+1——对应时刻dq轴电流值。
将式(2)代入式(1)后,即可求得永磁伺服驱动系统的离散预测模型为
式中: 上标k、k+1——对应时刻dq轴电压、电流、电角速度值。
至此,FCS-MPC采取二次型形式构建描述电流跟踪误差的价值函数g,即
通过将所有有效电压矢量对应k+1时刻电流预测值代入价值函数式(4),并采取枚举法逐一判断出最小值,即可确定最优的电压矢量。需要说明,每个开关器件均包含“开通”、“关断”两种开关状态,通过对6个开关器件(S1~S6)的不同状态组合,逆变器可输出23=8种不同电压矢量,包括:两个零电压矢量U0、U7(幅值为0)和六个有效电压矢量U1~U6(幅值为Udc),见图2。但是,考虑到功率开关器件的开关损耗、直通短路等问题,在实际系统的任一控制时刻,并非所有8个开关状态均可被切换,详细的开关状态切换规律参见表1。
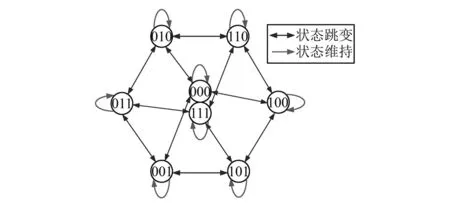
图2 三相全桥逆变系统开关状态切换图

k时刻开关状态k+1时刻候选开关状态000000、100、010、001001001、000、011、101010010、000、110、011011011、111、001、010100100、000、110、101101101、111、001、100110110、111、010、100111111、011、110、101
综上可知,由于两电平拓扑可输出的有效电压矢量局限性,加之开关状态限制造成的部分电压矢量不可行,故FCS-MPC最优解的精度难以得到保证。图3给出了15 kW样机参数下的FCS-MPC稳态仿真结果,其中图3(a)、图3(b)中αβ坐标系下稳态电流误差矢量幅值已达到10%以上,且图3(c)中电机电流频谱分析结果无特征次规律,大量谐波分量出现在2 kHz以内的低频段,上述谐波分量势必造成电机稳态运行品质降低。

图3 15 kW样机参数下的FCS-MPC稳态仿真结果
2 MCS-MPC原理
2.1虚拟电压矢量概念
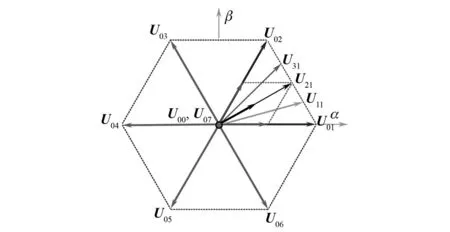
图4 有效电压矢量和虚拟电压矢量关系
为了克服传统FCS-MPC存在的稳态电流脉动问题,本文提出了一种基于MCS预测控制的PMSM电流脉动抑制方法,下文简称为MCS-MPC。所谓MCS,即在原有FCS-MPC中真实存在的有效电压矢量U0~U7基础上,叠加一系列虚拟电压矢量,如图4所示。图4中各扇区内均匀等分Nm个虚拟矢量,各扇区虚拟矢量由相邻的两个有效电压矢量组合而成。
式中:m——虚拟矢量所处扇区号;
n——虚拟矢量在所处扇区内编号。
虚拟矢量幅值和相位分别为
为了满足PMSM驱动系统低速运行要求,在虚拟电压矢量中进一步加入占空比概念,以调节逆变器输出端口电压幅值,见图5,即
式中:dmn——虚拟电压矢量Umn的占空比,dmn∈[0,1]。
2.2优化最优解求解方法
在完成虚拟电压矢量建模的基础上,将式(7)代入价值函数式(4)可得修正后的MCS-MPC价值函数表达式为


图5 单个控制周期内虚拟矢量数量之间的关系和转换模式
显然,MCS-MPC系统包含无数个虚拟电压矢量,直接采取枚举法对式(8)进行最优解分析是不可行的。式(8)中包含表征扇区号的m、表征虚拟矢量方向的n以及表征矢量幅值的dmn,将预测模型式(3)代入后可得价值函数演变形式为
参数矩阵I和Wmn分别为
进而,将式(9)代入式(8)并将价值函数二次型展开可得
将式(12)中占空比dmn作为变量,显然此式是一个存在极小值的凸函数,对占空比dmn进行偏微分运算如下:
因此,直接对价值函数分析可求得理论最优占空比dmnopt为
由于参数矩阵I仅与采样时间、电机参数以及实时的电机运行状态有关,其中并不包含可供调节的电压矢量项,因此可将式(15)的最小值求解问题进一步转化为对第二项的最大值求解过程,即

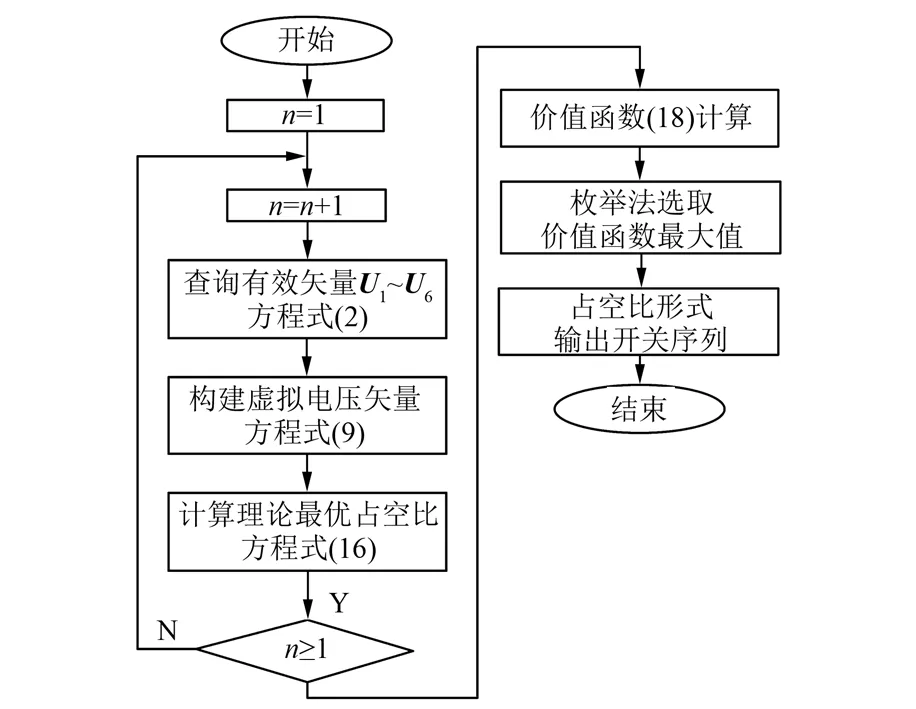
图6 MCS-MPC算法执行流程图
3 电流反馈噪声影响分析
对于实际采取MCS-MPC的PMSM驱动系统,另一个值得关注点是系统的参数鲁棒性问题。考虑到实际系统中存在电流反馈噪声Δis,价值函数式(9)中辅助矢量I与实际值I*存在一定的误差ΔI,即
式中:I*——反馈误差引入后的误差辅助矢量I;
ΔI——反馈噪声引起的辅助矢量I误差。
将式(17)代入预测模型式(3),可以看出,辅助矢量I误差ΔI为
式中: Δisd和Δisd——d、q轴电流反馈噪声。
对于PMSM一般情况下满足TcRs/Ld、TcRs/Lq≪1,此时ΔI可被简化为
从式(19)可以看出,d、q轴电流反馈噪声直接对辅助矢量I产生影响。由于反馈噪声的随机性,实际MCS-MPC系统中很难完成反馈噪声矢量ΔI辨识,但是随着虚拟电压矢量数Nm的增加,反馈噪声对辅助矢量I的影响随之变化,为此有必要对其规划规律展开分析。
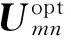

图7 I、ΔI和Wmn之间的几何关系
4 样机试验与结果分析
为了验证基于MCS-MPC的电流脉动抑制方法的可行性和有效性,搭建了如图8(a)所示的双15 kW PMSM对拖样机测试平台进行试验分析,控制系统采取TI公司TMS320F28335型号DSP,完成信号采样、系统保护、算法运算及上位机通信等诸多功能;图8(b)为MCS-MPC方法软件框图,其中速度外环采取PI调节器形式,数字系统中存在的控制延时问题,采取文献[12]中提及的软件二次预测方式进行补偿。本文此处不再赘述。

图8 双15 kW PMSM对拖样机测试平台
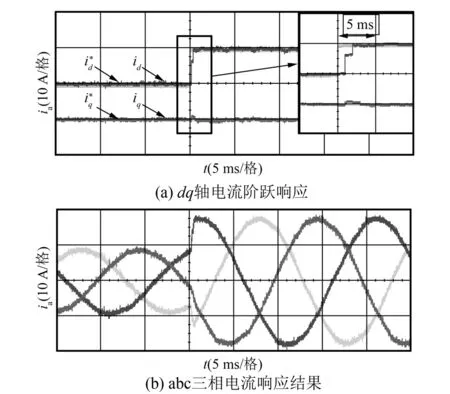
图9 MCS-MPC方法的动态跟踪性能
图9为MCS-MPC方法的动态跟踪性能试验结果,其中:图9(a)中dq轴电流给定值15 ms采取“阶跃”信号方式由10 A阶跃至20 A,在15 ms处阶跃发生时刻实际dq轴电流延时时间小于3 ms,表明此时MCS-MPC方法可快速完成转矩、磁链的动态调节,且调节过程中并未出现欠调制和超调制现象;图9(b)中abc三相电流正弦度高,进一步说明MCS-MPC输出电压矢量的正确性。综上可知,MCS-MPC方法保留了传统预测控制高动态响应特点,该特点对于本文研究的永磁伺服系统极具意义。

图10 FCS-MPC方法稳态性能测试结果
为了验证MCS-MPC方法对于PMSM伺服系统电流脉动抑制效果,图10、图11中给出了FCS-MPC与MCS-MPC方法稳态性能对比结果。对比内容包括:定子端口电压、a相电流及电流频谱。从图10可以看出,FCS-MPC稳态定子端口电压Uab并无规律性,各基波周期内开关动作时刻及开关频率存在一定的变化,虽然a相电流ia整体保持着较高的正弦度,总畸变率为5.5%,但其频谱分析结果中5次、7次及11次低频谐波分量比重较大,将会造成永磁同步电机伺服系统低频转矩脉动,同时引起电机出现一定程度的低频噪声;反观图11,由于加入了虚拟电压矢量的概念,传统FCS-MPC的有限控制集被扩展为有效控制集,MCS-MPC稳态定子端口电压Uab存在一定的规律性,在同样保持a相电流ia整体高正弦度的前提下,总畸变率仅为3.5%。其频谱分析结果中谐波分量多集中在开关频率2 kHz及其倍频附近。此时,PMSM伺服系统将表现为高频转矩脉动。考虑到高频谐波分量的易衰减特性,上述谐波对于伺服系统转矩影响极为有限,且通过增加低通滤波装置极易将其滤除。

图11 MCS-MPC方法稳态性能测试结果

图12 不同虚拟电压矢量数时电流反馈噪声影响
前面指出,不同的虚拟电压矢量数对于MCS-MPC系统抗噪声能力具有一定的影响,并得出减少虚拟电压矢量数Nm可提升电流反馈噪声的影响的结论。为了论证上述观点,图12给出了不同虚拟电压矢量数Nm时的MCS-MPC试验结果,其中:人为地将电流反馈环节增益配置为实际值的1.2倍以模拟反馈噪声。图12(a)中取虚拟电压矢量数Nm=8,图12(b)中取虚拟电压矢量数Nm=4。可以看出,在相同的反馈噪声影响下,Nm=8对应的dq轴电流稳态时出现明显静差,同时电流稳态也出现一定的不规则性脉动。反观图12(b)中Nm=4时的dq轴电流,其抗电流反馈噪声能力明显提升,即使出现一定程度的电流反馈增益偏量,其仍可实现高精度、无静差运行。表2进一步给出了4种不同虚拟电压矢量数Nm下的PMSM伺服系统运行结果,综合看来对于本文所采取的双15 kW试验样机,虚拟电压矢量数Nm=4时,系统在运行精度、计算耗时、抗扰动能力等多项指标上较为均衡。对于其他场合应用的MCS-MPC系统,需根据实际系统特性对虚拟电压矢量数Nm进行合理选取。

表2 不同虚拟电压矢量数时电流反馈噪声影响
5 结 语
为了克服传统FCS-MPC存在的稳态电流脉动问题,研究了一种基于MCS预测控制的PMSM电流脉动抑制方法,并基于双15 kW PMSM对拖样机测试平台进行试验分析,可以得出以下两点结论:
(1) MCS-MPC将电压源型逆变器有限的有效电压矢量数,扩展为多个以占空比形式存在的虚拟电压矢量,从而将传统FCS-MPC的有限控制集扩展为MCS,可有效抑制永磁同步电机伺服系统稳态电流脉动。
(2) 不同的虚拟电压矢量数对于MCS-MPC系统抗噪声能力具有一定的影响,且减少虚拟电压矢量数可提升电流反馈噪声的影响。因此,实际应用MCS-MPC系统时,需结合运行精度、计算耗时、抗扰动能力等多项指标进行虚拟电压矢量数的合理选取。
[1] 陈墨,胡昌华,张伟,等.新型无刷直流电动伺服机构设计与分析[J].电机与控制应用,2015,42(5): 6-10.
[2] 陈剑,程国扬.交流伺服电机高性能位置控制的试验研究[J].电机与控制应用,2014,41(2): 1-5.
[3] 熊琰,李叶松.基于频率特性搜索的伺服系统谐振控制[J].电气传动,2015,45(2): 39-44.
[4] TIITIENE P, POHJALAINEN P, LALU J. The next generation motor control method: direct torque control (DTC)[J].Epe Journal European Power Electronics & Drives,2015,5(1): 14-18.
[5] 刘向杰,孔小兵.电力工业复杂系统模型预测控制——现状与发展[J].中国电机工程学报,2013,33(5): 79-85.
[7] 周昆,孙明玮,陈增强.快速显式预测控制在倒立摆系统中的应用[J].仪器仪表学报,2014,35(9): 2037-2044.
[8] 曹晓冬,谭国俊,王从刚,等.一种低开关频率PWM整流器的满意预测控制策略[J].中国电机工程学报,2013,33(27): 69-77.
[9] 曹晓冬,谭国俊,王从刚,等.三电平PWM整流器多模型预测控制方法[J].电工技术学报,2014,29(8): 142-150.
[10] BORDONS C, MONTERO C. Basic principles of MPC for power converters: bridging the gap between theory and practice[J].IEEE Industrial Electronics Magazine,2015,9(3): 31-43.
[11] LIM C S, LEVI E, JONES M, et al. A comparative study of synchronous current control schemes based on FCS-MPC and PI-PWM for a two-motor three-phase drive[J].IEEE Transactions on Industrial Electronics,2014,61(8): 3867-3878.
[12] CORTES P, RODRIGUEZ J, SILVA C, et al. Delay compensation in model predictive current control of a three-phase inverter[J].IEEE Transactions on Industrial Electronics,2012,59(2): 1323-1325.
PMSMCurrentRippleSuppressionMethodBasedonMixingControlSetModelPredictiveControl*
CHENGTan1,SUZongyu1,ZHENWei1,NIUJianping2
(1. State Grid of Benxi Power Supply Company in Liaoning, Benxi 117000, China;2. School of Electrical Engineering, Shenyang University, Shenyang 110000, China)
In recent years, model predictive control technology (MPC) widely used in the high dynamic performance of motor drive system, in order to overcome the traditional MPC technology limited control set (FCS) steady current pulsation problem, a kind of based on mixing control set (MCS) predictive control method of all-digital fuzzy current ripple suppression was put forward. First of all, the analysis of discrete mathematics model all-digital fuzzy predictive control system, and the precision of voltage vector and the correlation between current ripple was analyzed. On this basis, the MCS-MPC would voltage source inverter limited number of effective voltage vector, extended to multiple compared with the form of virtual voltage vector, and based on the above online virtual voltage vector to complete the MPC optimization problem; In addition, considering the MCS-MPC system parameter sensitivity problem, analyzed the MCS-MPC system feedback noise problems were discussed. Finally, set up double 15 kW permanent magnet synchronous motor for prototype test platform for experimental analysis, content analysis including the MCS method of dynamic characteristics, current ripple effect of the steady state. The experimental results showed that the proposed MCS-MPC method in retained the traditional predictive control technology, on the basis of high dynamic response, which could effectively reduce the noise of all-digital fuzzy steady current pulsation and operation.
permanentmagnetsynchronousmotor(PMSM);modelpredictivecontrol(MPC);mixingcontrolset(MCS);currentripplesuppression
国家自然科学基金资助项目(50274052)
程 坦(1978—),男,工程师,研究方向为现代电网分析及其软件系统优化。
牛建平(1962—),男,教授,研究方向为高精度伺服电机驱动系统及其优化控制方法。
TM 351
A
1673-6540(2017)10- 0001- 07
2017 -04 -10

