多元变量最值问题的求解策略与探究
江苏省丹阳市教师发展中心(212300) 汪正文
多元变量最值问题的求解策略与探究
江苏省丹阳市教师发展中心(212300) 汪正文
多元变量最值问题在近几年高考或各类测试中频频亮相.由于其综合性强,思维跨度大以及对变形化归能力要求高等特点,常成为小题中的压轴题.此类问题若缺乏一些必要的策略与应对方法,往往使解题陷入困境.本文就以近几年高考题或模拟题为例剖析解决此类问题的一些有效策略,以飨读者.
一、消元法
多元变量问题最基本的思路就是将多元化为一元或二元问题,从而将问题转化为求函数最值或利用不等式知识予以解决.
1.代入消元
利用已知条件中的等式,选择一个变量表示其余变量,将多元变量问题转化为函数的值域问题求解.
例1已知x,y,z∈R,且x+y+z=1,x2+y2+z2=3,则xyz的最大值为___.
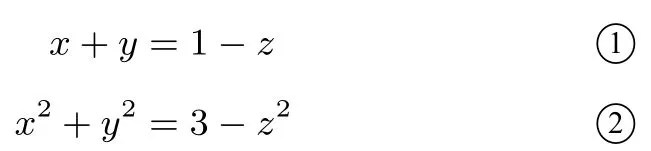
解析 由题意得,由1○2○得,xy=z2−z−1,则令f(z)=xyz=z3−z2−z,又利用导数知识即可解得
评注 根据已知条件,通过合理降元,化多元为一元,从而将问题转化为求函数的最值问题.本题没有引进新的变量,而是采用代入消元,但需挖掘隐含条件确定保留变量的范围.
2.放缩消元
利用不等关系,采用主元思想进行逐步放缩,从而达到降元的目的,同时需注意检验等号能否取得.
例2 若实数x,y,z,t满足1≤x≤y≤z≤t≤10000,则的最小值为____.
解析 由已知变量间的不等关系知,x≥1,t≤10000,z≥y,依次放缩x,t,z得,当且仅当x=1,t=10000,y=z=100时,不等式“=”成立,此时的最小值为
评注 本题是一个四元变量问题,条件是显性的不等关系,可先后视x,t,z为主元,利用单调性放缩成一元变量问题,再利用基本不等式予以求解.
例3 已知A,B,C是平面上任意三点,BC=a,CA=b,AB=c,则的最小值是____.
解析 由于A,B,C是平面上任意三点,则有a≤b+c,所以
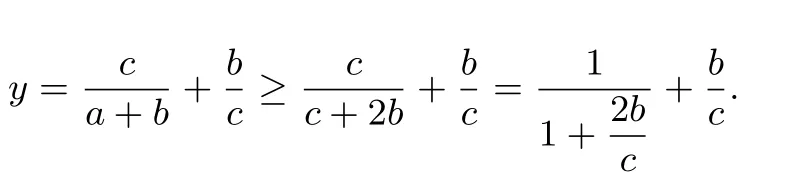
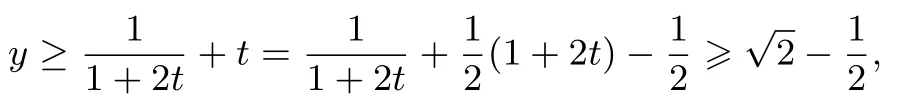
评注 本题利用隐性的不等关系a≤b+c,视y为a的函数,利用单调性将三元放缩为二元齐次式,再通过换元将问题转化为一元问题,最后利用基本不等式予以求解.
3.引参消元
解题时,有时需将式子的局部视为一个整体,通过引进新的变量代替它,以达到化简或消元的目的,从而起到将非标准型问题标准化、复杂问题简单化的效果.

图1
例4 已知函数f(x)=|x2+2x−1|,若a<b<−1且f(a)=f(b),则ab+a+b的取值范围是___.
解析 因为f(a)=f(b),由图1知,

即(a+1)2+(b+1)2=4.令其中θ∈[0,2π),则

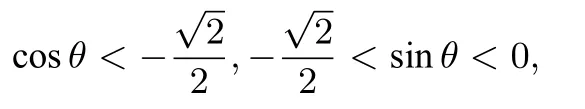
评注 本题中难以利用已知等式,采用a或b作为自变量代入消元,而需引进新的变量θ进行三角代换予以求解,本题的另一难点是需借助图像压缩a,b范围,再确定新元的范围.
例5 若实数x,y满足2x2+xy−y2= 1,则的最大值为___.
解析 条件可化为(2x−y)(x+y)= 1,令

评注 当条件可分解为ab=k(k为常数)的形式时,此时可令a=t,进行中值代换消元;若条件可变形为a+b=2m(m为常数)形式时,则可令a=m+t,b=m−t予以消元.当然,本题也可通过变形直接使用均值不等式求解,
二、构造法
构造法是根据已知条件和目标式子的结构特征与性质,抓住条件与结论间的内在联系,用已知条件中的元素为“元件”,以已知关系式为“支架”,在思维中构造出相关的新对象,使问题展现出来,并借助新对象使得原问题得到解决的思想方法.
1.构造函数
构造函数法是运用函数思想,对问题进行观察与分析,构造出与问题有一定联系的函数,再利用函数的性质将问题解决.
例6[1](美国第七届中学生数学竞赛题)已知a,b,c,d,e是满足a+b+c+d+e=8,a2+b2+c2+d2+e2=16的实数,试确定e的最大值.
解析 令

又f(x)的二项式系数为正且f(x)≥0,可知
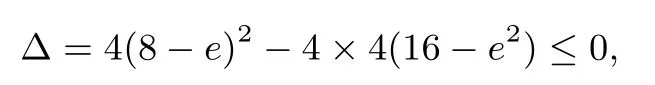
评注 直接利用条件来确定e的最值,非常困难,通过构造一元二次函数,由f(x)≥0恒成立,利用判别式即可快速求解,此法虽然巧妙,但其思维跨度大,构造之路异常艰辛.
2.构造斜率
例7 设正数a,b,c满足则的取值范围是___.
解析 由于b>0,则条件可化为


点P(x,y)表示图2中阴影部分,点,x∈设点Q(1,−2),则旋转直线QP不难发现,当直线QP与函数(x>0)的图像相切时,kQP最大.此时,设切点为切线
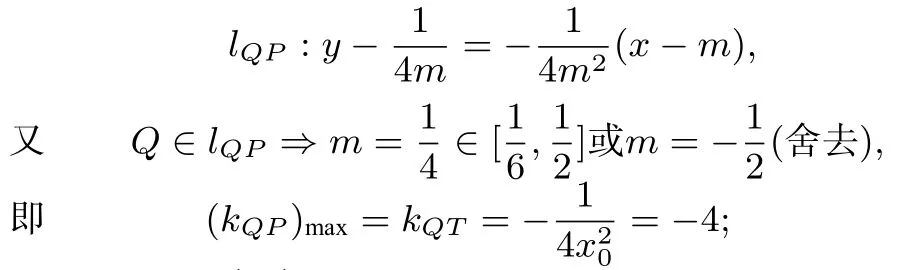
当P在点处时,kQP最小,即
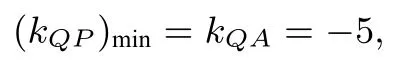
所以kQP∈[−5,−4].故的取值范围为[−4,−3].

图2
评注 当条件呈现出三元的多个不等式组时,可考虑通过重组变量,换元后转化为二元不等式组,再利用线性规划知识求解,本题中目标式子的斜率表征并不明显,需作适当的变形,方可揭示出其斜率本质.
3.构造距离
例8 已知x,y∈R,且y≥3,则(ex−y)2+(e−x−y)2的最小值为____.
解析 由目标式子的结构特征,可联想到距离的模型.式子(ex−y)2+(e−x−y)2可视为点 (ex,e−x)与点 (y,y)间的距离的平方d2,其中点 (ex,e−x)在曲线(x>0)上,点(y,y)在射线y=x(x≥3)上.设(x>0)上一点由图3知,动点(y,y)应在P(3,3)处,PN2最小,则

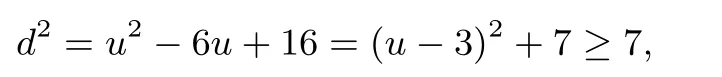
则当u=3,即时,(d2)min=7.

图3
评注 数形结合的关键是要能抓住式子的几何意义,但本题也极易误认为最小值是PM2=8,所以在运用数形结合解题时,一方面要借助“形”的直观性认识数,另一方面,还需将图像问题代数化,借助于“数”的精准来阐明“形”的属性,以获取正确的结论.另外本题也可通过换元,令ex+e−x=t,将问题转化为t的一元二次函数,再讨论求解.
例9 已知a,b∈R,a/=0,曲线,y=ax+4b+1.若两条曲线在区间[3,4]上至少有一个公共点,则a2+4b2的最小值是____.
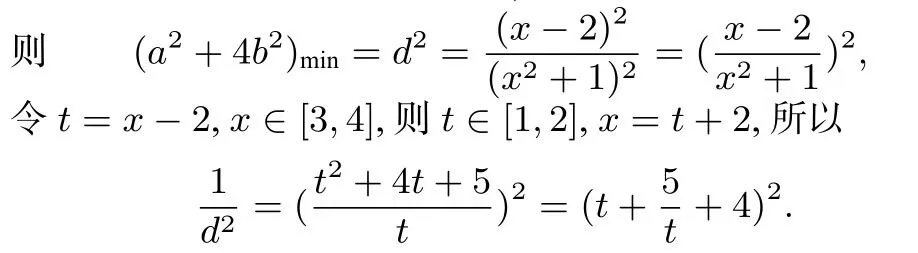
评注 本题若直接视为变量x的一元二次方程在[3,4]上有解,求出a,b间的不等关系,再利用线性规划知识求解,操作起来几乎不可能,但将方程视为点(a,2b)的直线,通过转换思维角度,将问题化归为求原点到直线的距离,从而达到出奇制胜的效果.
三、利用柯西不等式或基本不等式
例10 若正实数x,y满足(2xy−1)2=(5y+2)(y−2),则的最大值__________.
解析 本题看似无从下手,但若从基本不等式的结构特点考虑,则思路一目了然.由和有最大值,则平方和应为定值,故可考虑将条件向平方和方向变形.由
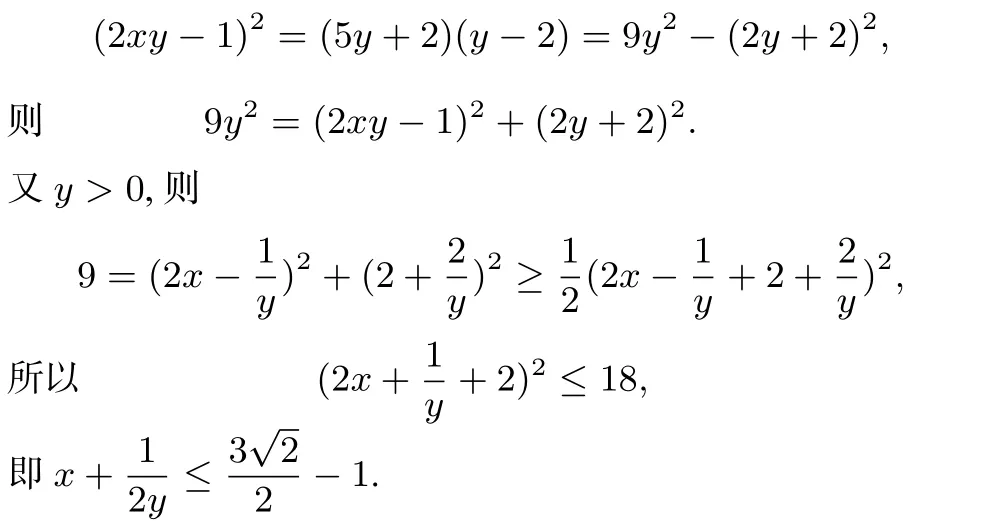
另解 由条件的结构特点联想到等比中项,由

成等比数列,设公比为q(q>1),将用q表示,则

评注 本题是通过观察结构特征,利用基本不等式求解,其关键是根据条件与结论的结构特点,辨明选用何种不等关系,从而提供变形方向;当然,也可令得2xy=2ty−1,将条件转化为关于y的一元二次方程,再利用判别式求解.
例11(数学通报问题522)已知x+2y+3z+4u+5v=30,求w=x2+2y2+3z2+4u2+5v2的最小值.

评注 本题利用其他方法无法求解,但根据条件和目标式的结构特点,利用柯西不等式迅速获解.
四、待定系数法
例12 若实数x,y∈R,且x2+2xy−y2=1,则x2+2y2的最小值是_______.
解析 由于条件和目标式均为齐次式,且主要呈现的是积与平方和的关系,可考虑利用待定系数法放缩为平方和的形式.设又
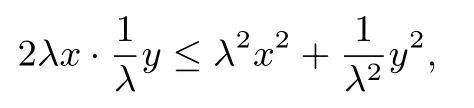

另解 设x2+2y2=r2,令则

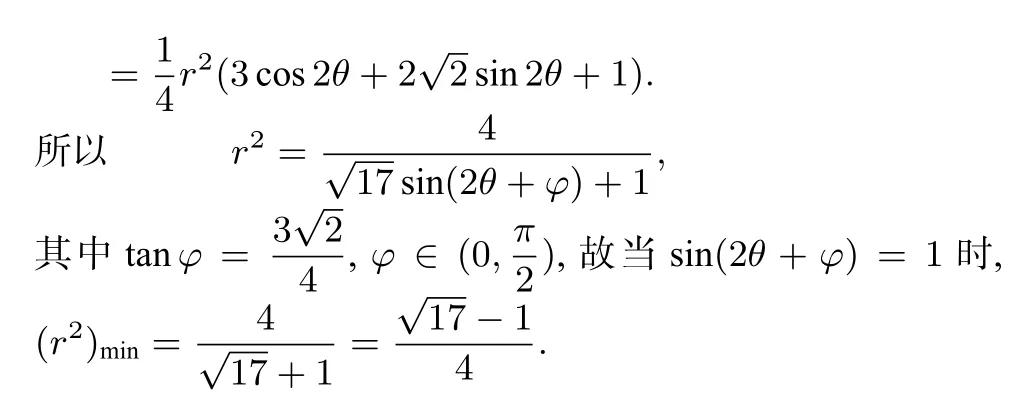
由于多变量函数最值问题的求解所涉及的知识面广,思维跨度大、方法灵活多样等特点,所以在面对具体问题时还需要用心观察,仔细推敲,同时不断加强学习和研究,只有这样,在面对此类问题时方能从容应对.
[1]张小雁.求一元或多元函数最值的若干策略[J].数学教学通讯,2014(3):55-56

