疲劳试验结果测量不确定度评定

(国防科技工业 5012二级计量站, 重庆 400023)

试验与研究

疲劳试验结果测量不确定度评定

冉学臣

(国防科技工业 5012二级计量站, 重庆 400023)

首先分析了疲劳试验结果测量不确定度的主要来源，然后采用不确定度传递律(GUM)评定方法，并结合旋转弯曲疲劳试验结果给出了成组法测定给定应力下疲劳寿命和升降法测定给定疲劳寿命下疲劳强度的测量不确定度的评定过程和结果。结果表明：可采用GUM法对旋转弯曲疲劳试验结果进行测量不确定度评定，成组法和升降法分别是确定疲劳寿命和疲劳强度的主要方法，该文介绍的评定方法对其他类型的疲劳试验结果的测量不确定度评定有一定的参考价值。

疲劳试验; 测量不确定度; 旋转弯曲疲劳试验; 成组法; 升降法

金属材料疲劳试验是评价材料力学性能和可靠性的重要方法之一，对疲劳试验结果进行测量不确定度评定，可以科学地评价疲劳试验结果的质量，也是满足CNAS-CL07:2011《测量不确定度的要求》对检测实验室测量不确定度评定的要求。疲劳试验结果测量不确定度的大小决定了疲劳试验结果的可信程度，会对疲劳试验结果的可信性、可比性和可接受性产生影响。正确地评定测量不确定度是满足客户、消费者和其他各有关方的期望和要求的需要。笔者通过对旋转弯曲疲劳试验结果进行评价，提出了疲劳试验结果的测量不确定度评定的思路和方法，可供其他类型疲劳试验参考。

1 试验材料与试验方法

试验材料为45钢φ25 mm棒材，炉号为OB1-1589，调质状态。取直径d=10 mm的漏斗试样,依据GB/T 4337-2015 《金属材料 疲劳试验 旋转弯曲方法》[1]，采用成组法测定疲劳寿命和升降法测定疲劳强度，试验环境温度为室温。依据JJF 1059.1-2012《测量不确定度评定与表示》[2]采用不确定度传递律(GUM)法对试验结果进行测量不确定度评定。

2 给定应力下疲劳寿命的测量不确定度评定

2.1建立数学模型

采用成组法进行疲劳试验时，通常给定应力下的疲劳寿命用Nf表示，因此测量模型可以表示为

或者表示为

式中：Nf为给定应力下的疲劳寿命，次；NM为从疲劳试验机上读取的疲劳寿命，次。

2.2不确定度来源分析

影响疲劳试验结果分散性的因素[3]主要有以下几个方面：①试验设备的不准确性；②试样尺寸和形状的不一致性；③试验材料的不均匀性；④试样加工过程的不一致性；⑤试样热处理过程的不一致性；⑥试验环境的偶然变异；等等。

这些因素是造成疲劳试验结果分散性的主要原因。其中第1条和第2条可以通过分析旋转弯曲疲劳试验机的弯曲应力和试样尺寸的测量不确定度分量来分析其对疲劳寿命试验结果的影响；第3～5条可以通过疲劳试验的重复性试验来估计；第6条可以通过严格控制环境条件来减小其对试验结果的影响。

鉴于以上分析，认为疲劳寿命的测量不确定度可以通过疲劳试验机不准确性引入的测量不确定度分量，以及试验重复性引入的测量不确定分量来合成，而环境条件的影响只要严格按试验方法控制可以忽略不计。

2.3试验重复性引入的测量不确定度分量ua

试验重复性引入的测量不确定度分量采用A类方法进行评定。

表1 成组法试验数据Tab.1 Test data for group method

2.4试验设备引入的测量不确定度分量u1

旋转弯曲试验机在试样上产生的弯曲应力S可根据下式计算

式中：S为旋转弯曲试验机在试样上产生的弯曲应力，MPa；M为旋转弯曲试验机产生的弯曲力矩，N·m；d为试样直径，mm。

弯曲应力的相对测量不确定度计算公式如下

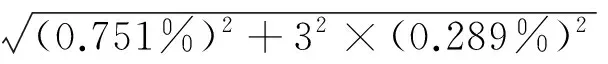
表1中应力水平和对数疲劳寿命的关系可按线性数学模型进行分析[4]，其函数关系如下

式中：lgNf为对数疲劳寿命；S为应力水平，MPa；a,b为线性方程的系数，常数[4]。

依据表1中的数据，可求出：a=-0.015 9，b=12.035，相关系数R=0.994 3。考虑S引入的不确定度，则u1=|a×u(S)|,由此可得到表2所示结果。

表2 试验设备对疲劳寿命的影响Tab.2 Influence of test equipment on fatigue life

2.5lgNf的合成标准不确定度

ua和u1可以认为相互独立，因此合成标准不确定度uc见表3。

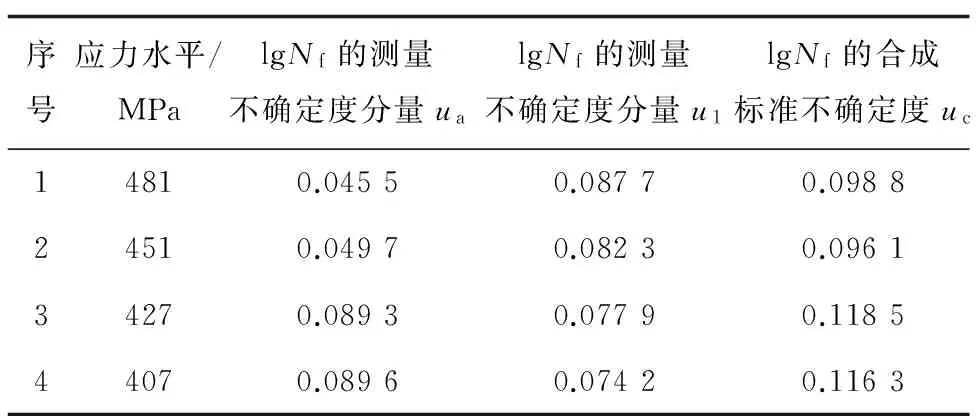
表3 给定应力下对数疲劳寿命的合成标准不确定度Tab.3 Combined standard uncertainty of logarithmic fatigue lifeunder given stress

2.6lgNf的扩展不确定度

取k=2，得到给定应力下对数疲劳寿命的扩展不确定度U，其结果如表4所示。

表4 给定应力下对数疲劳寿命的扩展不确定度U(k=2)Tab.4 Extended uncertainty U of logarithmic fatigue lifeunder given stress (k=2)

3 给定疲劳寿命下疲劳强度的测量不确定度评定

3.1建立数学模型

给定疲劳寿命下确定疲劳强度通常采用升降法进行试验。给定疲劳寿命下疲劳强度的数学模型可以用下式表示

3.2不确定度来源分析

影响疲劳强度的因素主要有：疲劳试验机不准确性和试样尺寸、形状不一致引入的测量不确定度分量，以及升降法引入的测量不确定分量。

3.3升降法引入的相对测量不确定度分量urel(a)

采用升降法确定的疲劳强度服从正态分布[3]，由此可以计算疲劳强度的平均值和试验标准差。

3.4试验设备和试样尺寸、形状不一致引入的相对测量不确定度分量urel(S)

采用与2.4节同样的方法可得到试验设备引入的相对测量不确定度分量为：urel(S)=1.147%。

3.5疲劳强度的合成标准不确定度uc

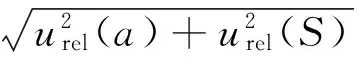
3.6疲劳强度的扩展不确定度U

取k=2，则扩展不确定度U=2×uc≈10 MPa。

4 结论

在假设对数疲劳寿命和疲劳强度满足正态分布的条件下，采用GUM法进行测量不确定度评定符合JJF 1059.1-2012规定的适用条件，可以采用GUM法开展给定应力下疲劳寿命和给定疲劳寿命下疲劳强度的测量不确定度评定。该文提出的评定方法同样适用于轴向加力等情况的疲劳试验结果的测量不确定度的评定。

[1] GB/T 4337-2015 金属材料 疲劳试验 旋转弯曲方法[S].

[2] JJF 1059.1-2012 测量不确定度评定与表示[S].

[3] 黄镇同.疲劳应用统计学[M].北京:国防工业出版社,1986.

[4] GB/T 24167-2009 金属材料 疲劳试验 数据统计方案和分析方法[S].

[5] 何雪浤,谢伟涛.几种常用的金属材料疲劳极限试验方法[J].理化检验-物理分册,2015,51(6):388-393.

[6] 白鑫,谢里阳,任俊刚,等.金属材料疲劳试验与数据处理方法[J].理化检验-物理分册,2015,51(6):375-380.

[7] 陈敬海,吴勇,单长伟,等.两种分布函数在曲轴扭转疲劳寿命分析中的应用[J].理化检验-物理分册,2016,52(11):781-785.

MeasurementUncertaintyEvaluationonFatigueTestingResults

RANXuechen

(Grade Two 5012 Metrological Station, National Defense Science and Technology Industry, Chongqing 400023, China)

The major sources of measurement uncertainty of fatigue testing results were analyzed. By adopting evaluation method of uncertainty transfer law (GUM method) and combined with the results of rotating bending fatigue testing, the measurement uncertainty evaluation procedure and results of fatigue life under given stress determined by group method and fatigue strength under given fatigue life determined by up-and-down method were given. The results show that GUM method can be used to evaluate the measurement uncertainty of the results of rotating bending fatigue testing. The group method and the up-and-down method are main methods to determine the fatigue life and fatigue strength, and the evaluation method introduced in this paper has a certain reference value for evaluation of the measurement uncertainty on other fatigue testing results.

fatigue testing; measurement uncertainty; rotating bending fatigue testing; group method; up-and-down method

TB114.3; TB302.1

A

1001-4012(2017)10-0717-03

10.11973/lhjy-wl201710005

2016-12-21

冉学臣(1963-)，男，研究员级高级工程师，主要从事力学计量、力学性能测试和疲劳试验工作，gf5012@126.com