借用隐形翅膀 寻找错误之源

李燕华

借用隐形翅膀 寻找错误之源

李燕华

“轴对称图形”是初中几何部分非常重要的章节，同学们在解决与轴对称相关的问题时，由于考虑问题不全面或识图能力的限制，常常会出现各种错误，下面就结合常见错误类型进行分析.

一、只凭经验误判断

例1 如图1，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（ ）.

图1

【错解】A.

【错解原因】根据直观想象，外面是个正方形，认为内部也是正方形，没考虑内部正方形的放置形式.

【正解】B.

【点评】对于折叠、展开的问题，亲自动手操作一下，可以培养空间想象能力.

二、概念不清引争议

例2 三角形ABC的三条内角平分线为AE、BF、CG，下面的说法中正确的有（ ）.

①△ABC的内角平分线上的点到三边距离相等；

②三角形的三条内角平分线交于一点；

③三角形的内角平分线位于三角形的内部；

④三角形的任一内角平分线将三角形分成面积相等的两部分.

【错解】①②③④.

【错解原因】在解题时不注意画图，如果能按题目要求画出图形，结合三角形内部角平分线性质，就能得出②③正确.选①的是概念、审题不清，以为“角平分线上的点”就是“角平分线的交点”；选④的是概念不清，应该是“三角形的中线将三角形分成面积相等的两部分”，而不是角平分线.

【正解】②③.

【点评】本题主要考查了三角形的角平分线性质和三角形的中线性质，要多画图思考，增强推理能力和辨析能力.

三、折叠问题易出错

例3 如图2，将边长为8cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长度是（ ）.

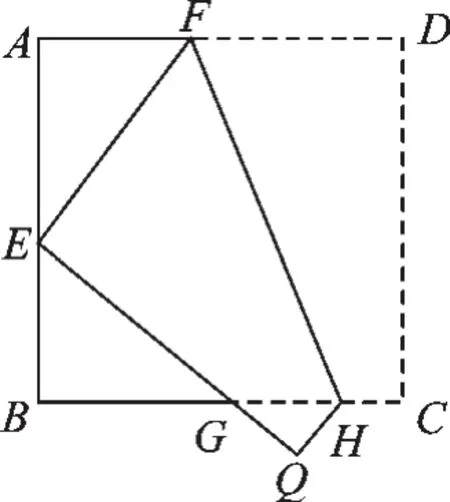
图2

A.2cm B.2.5cm C.3cm D.3.5cm

【错解】B.

【错解原因】不能准确理解图形折叠前后可以得到的信息，无法构建基本数学模型.

解：由折叠可得DF=EF，设AF=x，则EF=8-x，∵AF2+AE2=EF2，∴x2+42=（8-x）2，解得x=3.

【正解】C.

【点评】本题考查折叠问题，一定要抓住翻折前后得到的图形是全等的（这里主要利用对应边相等），再找到相应的直角三角形，利用勾股定理求解.

四、作图问题易漏点

例4 如图3，直线AB、CD是两条交叉的公路，且交于点E，现在要建一个商店，要求它到两公路的距离相等且离点E有300米，则可供选择的地址有（ ）处.

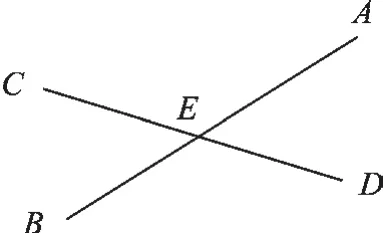
图3

【错解】2.

【错解原因】如图4，考虑问题不全面，以为商店在两条公路所成角∠AED、∠CEB的角平分线与以点E为圆心、300米为半径的圆的交点上，忽略了∠AEC、∠DEB的角平分线与圆的交点.

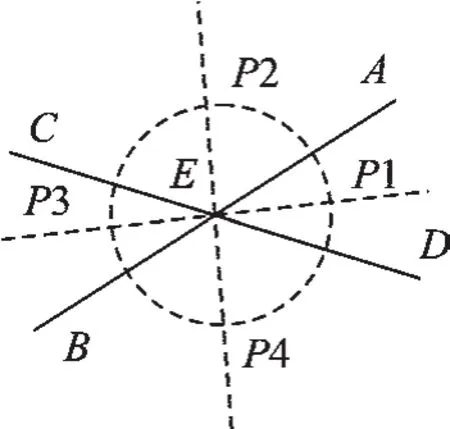
图4

【正解】4.

【点评】本题主要考查了角平分线的性质、圆的定义等知识，需要注意的是，两条直线相交成4个角，这4个角的角平分线上的点到两条直线的距离都相等.

五、分类不清致错误

例5 如图5，网格中的每个小正方形的边长为1，A、B是格点，以A、B、C为等腰三角形顶点的所有格点C的个数为 个.

图5

【错解】2.

【错解原因】直接用眼睛观察，以A、B为顶点和以AB为腰的等腰三角形各有一个，所以就填2.

图6

解：如图6，根据等腰三角形的定义，应该画“两圆一直线”，即分别以A、B为圆心，AB长为半径画弧，再作线段AB的垂直平分线，定点C的位置如图6.故有8个.

【正解】8.

【点评】本题主要考查了等腰三角形的判断，解题时需要通过尺规作图，找出点C的位置.掌握等腰三角形的判定、分情况讨论是解决问题的关键.

轴对称图形是图形变换的重要组成部分，也是中考命题的热点，涉及的知识点较多，特别是等腰三角形的性质和判定.所以我们在学习这一章时，要能结合图形理解掌握所学的知识，并灵活应用，融会贯通.

（作者单位：江苏省常州市新北区小河中学）