转向机动条件下的拖线阵WP模型适用性研究

奚畅，蔡志明，袁骏



转向机动条件下的拖线阵WP模型适用性研究

奚畅，蔡志明，袁骏

(海军工程大学电子工程学院水声工程系，湖北武汉430033)

阵形估计是拖曳阵声呐在拖船转向机动情况下不能回避的问题。已知的Water-Pulley(WP)模型所需信息易于获取，运算复杂度小并且可以预判阵形，在工程实际中有一定应用价值。但WP模型稳健性有限，阵形估计效果受拖船机动情况影响较大。为探究WP模型适用性以指导拖船机动避免模型失效，首先通过计算机仿真证明拖船转弯半径是最主要的影响因素；然后提出一种以最大测向误差和最大增益损失为模型适用准则，结合某船旋回特性以指导拖船机动的方法；最后分析了存在水流扰动时应注意的拖船机动情况。

阵形估计；转向机动；Water-Pulley模型

0 引言

直线机动是拖线阵声呐在使用过程中的必要工况，但舰船在保证对敌有利观测范围、规避鱼雷等情况下，需要进行转向机动。由于拖线阵声呐自身的柔性结构、向大尺度发展的趋势以及海流扰动的影响，在转向过程中不可避免地会发生阵形畸变。一般认为在阵形畸变超过接收信号波长的1/10时，就应在波束形成时对阵形畸变做出补偿[1]，否则会造成主瓣形状畸形、旁瓣级升高、输出信噪比下降。因此，有效地估计阵形是提高转向机动条件下拖线阵探测性能的关键。

Paidoussis方程描述了零浮力柔性细长圆柱体在流体中的运动状态，它是根据一小段长度柱体的受力平衡原理得到的[2]。Kennedy通过化简Paidoussis方程及实验验证得出结论，当阵长远大于缆径并且阵受匀速直线拖曳时，Paidoussis方程可以简化为Water-Pulley(WP)模型[3]。Peter Gerstoft通过实验证明，当阵受拖曳的方向发生较小变化时，WP模型依然能够描述拖线阵运动状态[4]，但没有进一步说明WP模型的失效条件。

WP模型具有所需信息易于获取、运算复杂度小、可预判阵形等优点，但由于它是经过化简得到的，稳健性不够，存在一定的适用条件。本文基于WP模型，通过计算机仿真，依据波束形成性能，分析拖船转向机动对WP模型阵形估计效果的影响，探究WP模型的适用性，用于指导拖船机动，使得在拖船转向机动过程中仍可用WP模型较好地估计阵形。

1 WP模型的原理及公式

Paidoussis通过分析一小段长度的柔性零浮力柱体在流体中的受力情况，得出描述其小幅自由横向运动的方程(Paidoussis方程)为

当拖线阵长度远大于直径时，Paidoussis方程可以简化为小直径的Paidoussis方程(Small Diameter Paidoussis，SDP)，如式(2)所示：

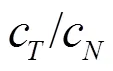
从式(3)可以看出，拖线阵横向偏移量从阵首到阵尾无损失地传递。因此可以认为阵中每个点都沿着上一个点的轨迹运动，可以将拖船航迹认为是拖线阵阵形。因此可以根据拖船全球定位系统(Global Positioning System，GPS)数据拟合出航迹，再利用拖船航速、放缆长度以及阵元间距估计各个阵元的位置。WP模型具有所需信息易于获取、运算复杂度小、可以预判阵形等优点。

2 WP模型的影响因素分析

当拖船发生机动时，驾驶员能够控制的因素包括推进器档位、舵角和转向时间，此三方面主观因素与船本身的性质共同决定了船的转弯角度、转弯半径以及航速。拖缆的运动是受拖点驱动的，所以着重分析静水中拖船的转弯角度、转弯半径以及航速对WP模型阵形估计效果的影响。

当估计阵形与真实阵形各自的首尾阵元连线的法向方向相差较大时，会增大目标方位估计误差；当首尾阵元连线的法向方向相差不大，但阵列流形存在较大差别时，会降低基阵增益。所以，选择测向误差和增益损失作为评价阵形估计效果的指标。

Ablow[6]提出的拖缆运动方程模型可以计算不同航速定常直航、不定常运动、考虑海流及船舶有升沉等多种运动状态下阵列的阵形与姿态。Ablow模型计算所得数据与1980年Rispin[7]通过一系列海试得到的数据具有较好的一致性，因此，在仿真时认为通过Ablow模型计算得到的阵形是真实阵形。

在仿真过程中，采用表1所示的参数，阵元个数为60，阵元间距为4 m，通过Ablow提出的拖缆运动方程模型计算得到较为准确的阵形，认为是真实阵形(图1中点画线部分)，再利用拖船航迹(图1中虚线部分)和放缆信息得出WP模型估计结果(图1中实线部分)。用估计阵形的阵列流形矢量对真实阵形接收到的远场平面波信号做常规波束形成，可以得到如图2所示的波束图。认为波束图中增益最大处对应的角度与90°(图2中虚线部分)之间的偏移量是测向误差，认为波束图中最大增益与60个阵元对应的阵增益即17.78 dB之间的差值是增益损失。

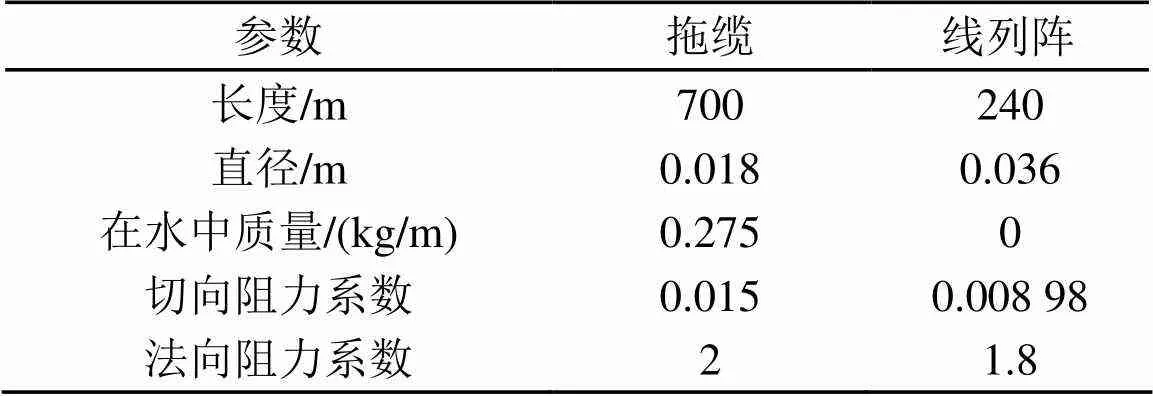
表1 拖线阵参数

图1 估计阵形与真实阵形

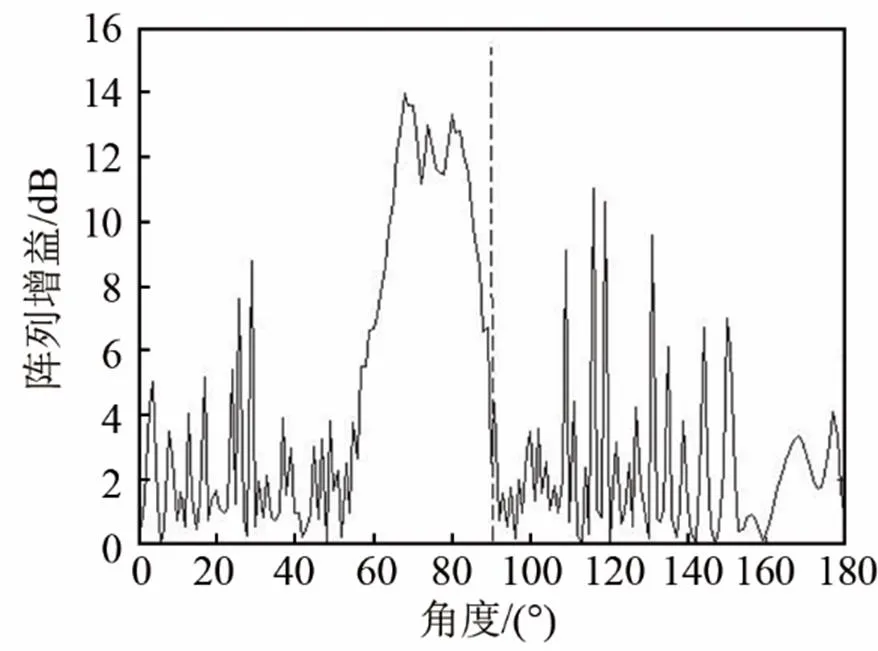
图2 估计阵型的波束图

在仿真过程中，用控制变量的方法分别改变拖船的航速、转弯半径、转弯角度。计算由于阵形估计误差造成的、拖船转向机动过程中的平均测向误差和平均增益损失。具体参数变化情况及仿真结果如图3~5所示。

从图3~5中可以看出，与转弯角度和航速相比，转弯半径的变化能够引起测向误差和增益损失更大幅的变化，且变化趋势与理论结果相符。可以得出结论，转弯半径是拖船转向机动过程中影响WP模型阵形估计效果的最主要因素，转弯角度的变化对测向误差存在一定影响，航速变化对增益损失存在一定影响。

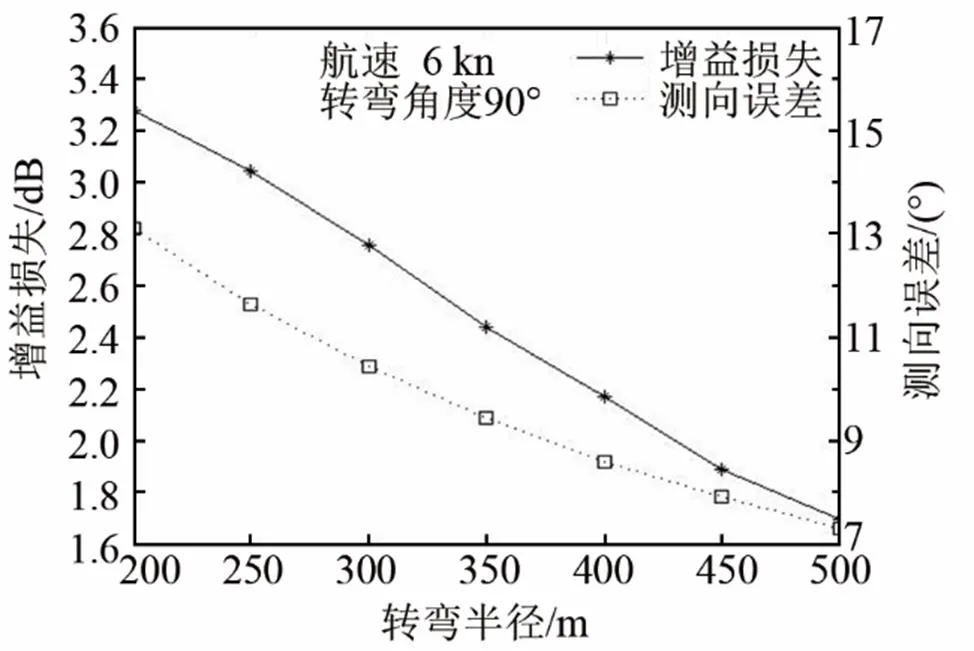
图3 增益损失和测向误差随转弯半径变化情况

图4 增益损失和测向误差随转弯角度变化情况

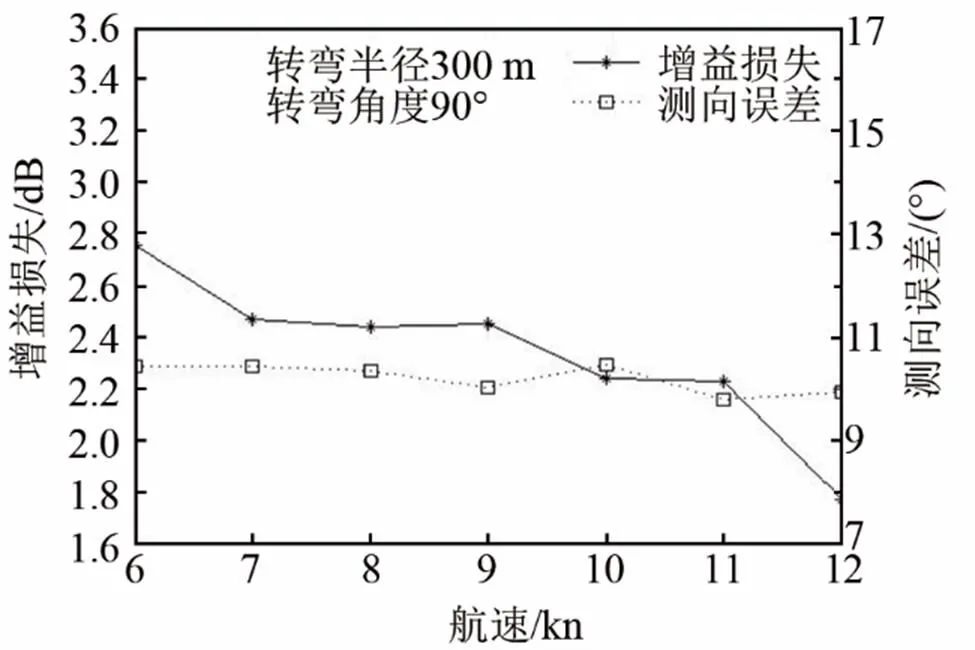
图5 增益损失和测向误差随航速变化情况

3 WP模型适用性分析

3.1 静水条件下

当拖船航速和转弯角度一定时，只要给定一个转弯半径，就能仿真出其转向机动过程中的平均测向误差和增益损失。当拖船以6 kn航速转过90°，转弯半径在200~500 m内间隔10 m变化时的测向误差和增益损失变化情况，如图6所示。

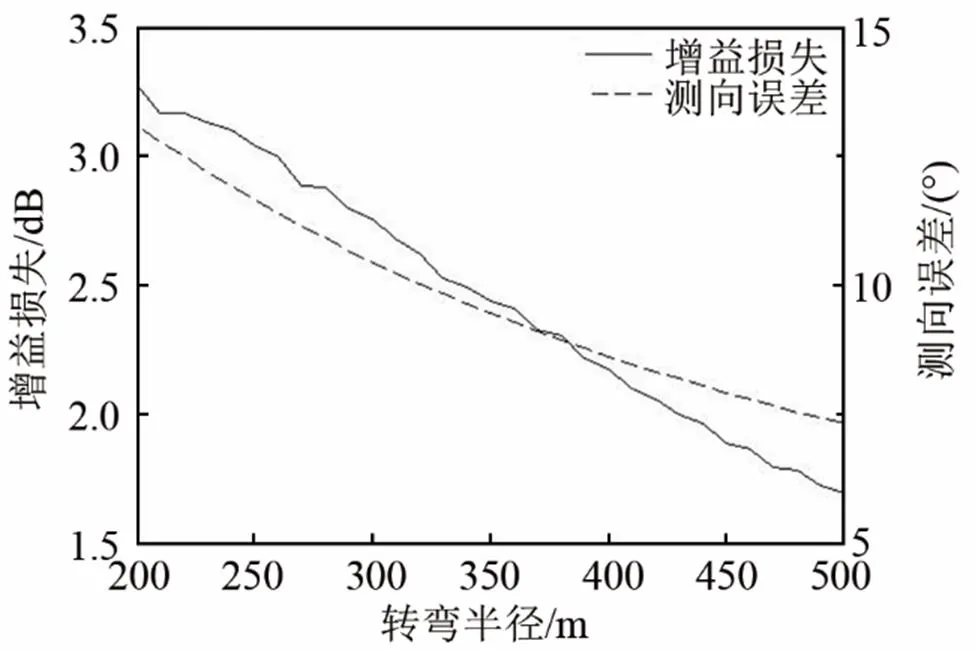
图6 测向误差和增益损失随转弯半径变化情况(间隔10米)

可以认为测向误差和增益损失是转弯半径的一元次多项式，通过试验可知，当等于3时拟合曲线基本上与仿真所得曲线重合，此时测向误差和增益损失可以表示为式(4)、式(5)所示的一元三次多项式形式：

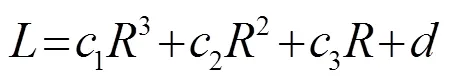
将图6中的数据用MATLAB软件进行拟合，拟合系数如表2所示。

表2 测向误差和增益损失曲线的拟合系数

拖线阵在使用过程中，为控制拖线阵中声阵部分的深度，减少流噪声干扰，避免拖点处拉力过大，拖船航速一般定为6～8 kn。某型实验船在静水环境下车钟进一状态时，航速刚好在6 kn左右。由此船旋回要素测定实验得到车钟进一状态下不同舵角对应的转弯半径，又由船舶操纵运动方程[8]可知转弯半径随舵角的变化情况应是单调且可导的，因此可拟合出车钟进一情况下舵角与转弯半径的关系如图7所示。

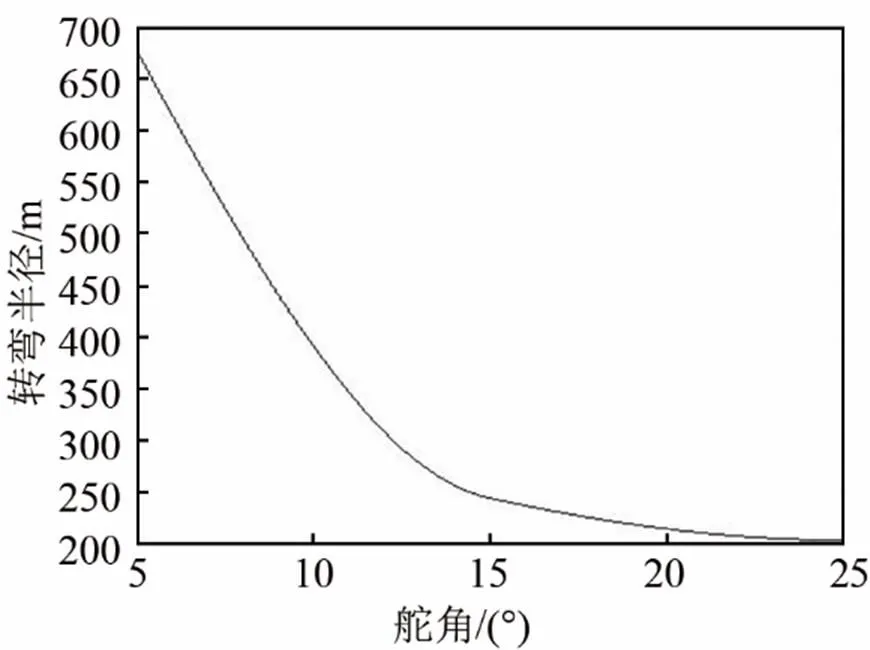
图7 某船车钟进一时的旋回性能

因此，在此型船发生机动并用WP模型估计阵形时，为保证一定的波束形成效果，可在根据式(4)、式(5)确定允许的最小转弯半径后，依据图7，查表确定最大舵角，以指导拖船机动。例如，当允许的最大测向误差和阵列增益损失分别是10°和2.5 dB时，转弯半径需大于340 m，舵角需小于11°。

3.2 考虑水流影响时

拖线阵声呐在实际使用的过程中会受到水流扰动的影响，设计下述仿真，分析存在水流扰动时的WP模型适用性。

当水流速度为1 m/s，拖船航速为6 kn，顺时针转过90°，初始航向顺时针方向旋转至水流流向的旋转角度分别为0°、90°、180°、270°，仿真转弯半径在200~500 m内间隔10 m变化时，仿真测向误差和增益损失的变化情况。

由图8所示的仿真结果可知，当有与拖船初始方向相同流向的水流时，WP模型阵形估计结果略好于静水时，转向机动时可以用略大于查表所得值的舵角；存在其他方向水流时，阵形估计结果与静水时相比都有不同程度的恶化，在拖船机动时需要更小的舵角。

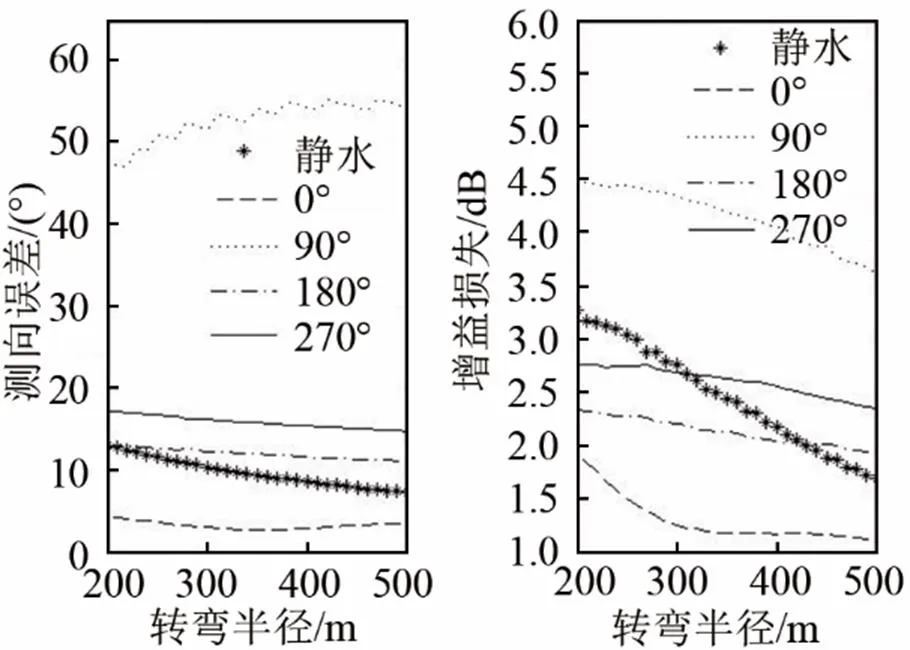
图8 考虑水流时测向误差和增益损失随转弯半径的变化情况

4 结语

本文通过计算机仿真，依据波束形成性能，首先证明在拖船转向机动时，转弯半径是影响WP模型阵形估计效果的最主要因素。然后探究了如何根据允许的最大测向误差和增益损失，结合拖船旋回特性，得出对于拖船机动的指导，使得在拖船机动时用WP模型估计的阵形仍能保证一定的波束形成效果。最后分析了存在水流扰动时拖船转向机动应注意的问题。

下一步的工作是利用实际海试数据对结论进行验证。

[1] 刘孟庵. 拖曳线列阵声呐技术发展综述[J]. 声学与电子工程, 2006, 21(3): 1-5. LIU Mengan. Summary of towed array sonar technology development[J]. Acoustics and Electronics Engineering, 2006, 21(3): 1-5.

[2] Paidoussis M. Dynamics of flexible slender cylinders in axial flow[J]. Fluid Mech, 1966, 26(4): 717-736.

[3] Kennedy R M. Crosstrack dynamics of a long cable towed in the ocean[J]. IEEE Oceans, 1981: 966-970.

[4] Peter Gerstoft, William S Hodgkiss, Kuperman W A, et al. Adaptive beamforming of a towed array during a turn[J]. IEEE Journal of Oceanic Engineering, 2003, 28(1): 44-54.

[5] Gray D A, Anderson B D O, Bitmead R R. Towed Array shape estimation using kalman filters-theoretical models[J]. IEEE J. Oceanic Eng, 1993, 18(4): 543-556.

[6] Ablow C M. Schechter S. Numerical Simulation of Undersea Cable Dynamics[J]. Ocean Engng, 1983, 10(6): 443-457.

[7] Rispin P. Data package No.1 for cable and array maneuvering[R]. Naval Ship Research and Development Center, Bethesda, Maryland. 1980.

[8] 洪碧光. 船舶操纵原理与技术[M]. 大连: 大连海事大学出版社, 2007: 45-57. HONG Biguang. Ship handling principle and technology[M]. Dalian: Dalian Maritime University Press, 2007: 45-57.

Investigation of the applicability of Water-Pulley model during ship’s maneuvering

XI Chang, CAI Zhi-ming, YUAN Jun

(Department of Underwater Acoustic Engineering, College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China)

Array shape estimation of towed array sonar is an important problem that cannot be ignored during ship’s maneuvering. The existing water-pulley model (called WP model) has certain application value due to easily obtaining required information, less computational complexity and being able to predict the array shape. But, the robustness of the WP model is limited. Ship’s maneuvering has great impact on array shape estimation. In order to explore the applicability of the model to guide ship’s maneuvering and to avoid the model failure, the paper firstly makes simulation to prove that the turning radius is the most important factor, and then proposes a method to guide ship’s maneuvering according to the model applicable criterion of maximum direction error and maximum gain loss. Finally the effect of flow disturbance on ship’s maneuvering is analyzed.

array shape estimation; steering maneuver; water-pulley model

TN911.7

A

1000-3630(2017)-02-0123-05

10.16300/j.cnki.1000-3630.2017.02.005

2016-05-07;

2016-07-10

奚畅(1992－), 男, 河北保定人, 硕士研究生, 研究方向为水声信号处理技术与应用。

奚畅, E-mail: xichangwxx@163.com