基于多频率数据融合的Lamb波损伤定位研究

杨晓华，刘学君，马广婷



基于多频率数据融合的Lamb波损伤定位研究

杨晓华1，刘学君1，马广婷2

(1. 海军航空工程学院青岛校区航空机械系，山东青岛266041；2. 91899部队，辽宁葫芦岛125001)

确定损伤位置是结构健康监测中的重要环节，而时间延迟是确定损伤位置的关键问题。针对Lamb波的频散效应对定位精度的影响，提出了一种基于Morlet小波时频分析和多频率数据融合的损伤定位方法，首先采用小波分析的手段，提取多组特定频率下的信号，实现多频率成分下波达时刻的准确判定，进而采用加权平均处理的方法获得损伤位置到两换能器的距离之和，最后基于椭圆定位法确定了损伤的位置。试验结果表明，该方法能够有效减少Lamb波频散效应的影响，相较时域峰值包络的方法，可有效提高定位的精度，同时增强了系统抗干扰的能力。

Lamb波；Morlet小波；椭圆定位法；数据融合；时间延迟

0 引言

近年来，基于导波的飞机结构健康监测技术引起了研究人员的广泛关注。Lamb波是在板类结构中传播的导波，可以由压电换能器、磁致伸缩换能器等激发和感知，具有易激发、传播距离远及监测范围大等特点，是对薄板类结构如飞机蒙皮等进行在线监测的有效手段。结构健康监测的主要任务有：判断是否存在损伤、定位损伤的位置、评估损伤的类型及程度、分析预测结构寿命及评估结构安全性等，而定位损伤的位置是结构健康监测中的重要环节[1-5]。

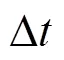
彭鸽等[12]利用信号传播时间(Time of fight, Tof)，对健康信号与含损伤信号的差信号进行分析，采用椭圆定位法进行了损伤定位研究；LU Y等[13]采用时域信号包络法，确定了时间延迟，采用椭圆定位法初步确定损伤位置，进而采用全加的数据融合方法对多传感路径进行综合定位，并成像处理。上述方法均是基于对信号时域波形的分析，但由于Lamb波的频散特性，即不同频率下的Lamb波群速度不同，可能会导致信号时域波包的变形，造成时间延迟的计算不准确，进而导致定位失准。为消除频散效应的影响，严宏等[14]基于小波分析及概率统计理论，利用健康信号与差信号的能量差作为损伤指标，提出了一种损伤存在概率成像算法。基于时频变换的方法对换能器接收的信号进行处理，可有效消除Lamb波的频散影响，进而获得较为准确的时间延迟，最终可提高定位精度。

本文采用Morlet小波分别对健康信号和损伤信号进行时频分析，通过提取激励信号中心频率和其附近频率的时域信号，确定多个频率下的时间延迟，结合对应频率下的相速度，确定板中离散点到换能器对的距离之和，对多个频率下的距离之和进行加权处理，进而采用椭圆定位法确定损伤位置。

1 Lamb波传播理论

Lamb波是板状结构中产生的平面应变波，且在板的上、下表面应力为零，可划分为对称模态和反对称模态。Lamb波的群速度及相速度可根据Rayleigh-Lamb波方程得到[1]：

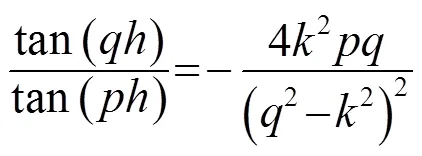
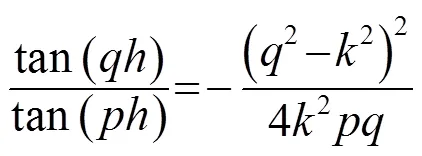
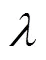
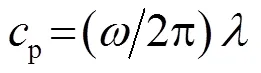
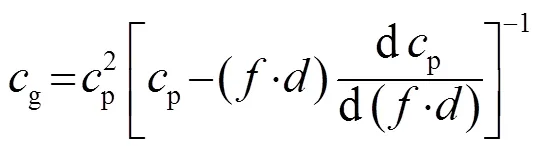
其中，=2为板厚。

针对LY12CZ铝合金材料，其弹性模量为73 MPa，泊松比为0.33，密度为2 780 kg/m3，横波波速为3 142 m/s，纵波波速为6 237 m/s，采用二分法，通过MATLAB编程对频散曲线进行了数值求解，群速度和相速度频散曲线如图1和图2所示。

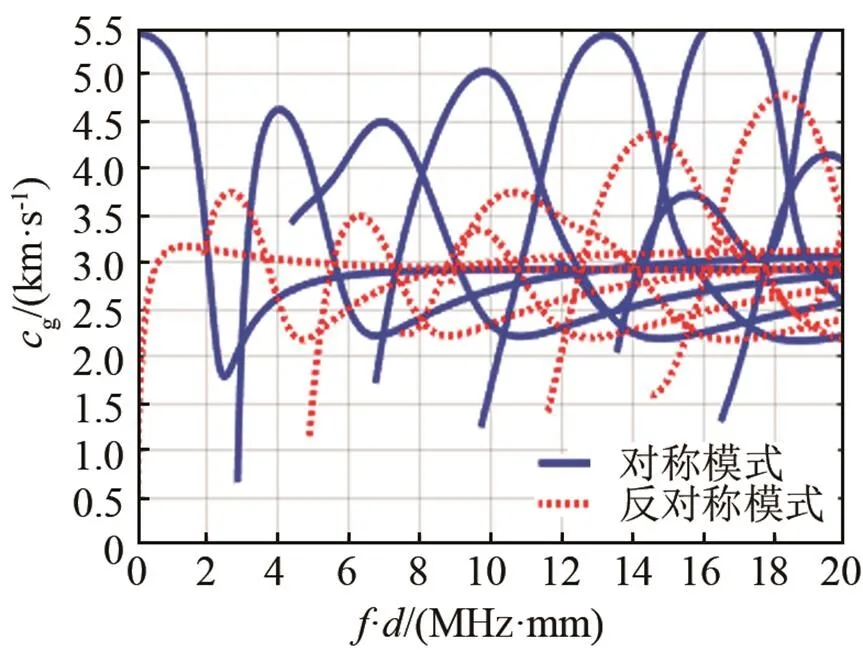
图1 群速度频散曲线

图2 相速度频散曲线

2 椭圆定位法

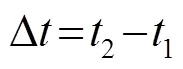
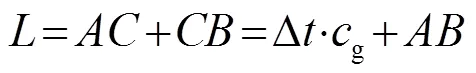
式中：是损伤到两换能器的距离之和。损伤必然发生在以两换能器为焦点，且到达两焦点距离之和为g的椭圆上。因一对换能器只能确定一个椭圆，无法实现损伤定位，故采用三个以上的换能器进行定位，多个椭圆的交点即为损伤位置。

图3 椭圆定位法示意图

Fig.3 The schematic of Ellipse localization method

3 基于Morlet小波时频分析及数据融合的椭圆定位法

3.1 基于Morlet小波变换的时间延迟确定方法

目前常用的时频分析方法有短时傅里叶变换(Short-Time Fourier Transform，STFT)、Wigner-Ville分布和小波变换等。短时傅里叶变换是采用固定的窗函数，窗函数一旦确定，则时频变换的分辨率就已确定，且不能兼顾时间和频率的分辨率，仅适合于缓变信号的分析；Wigner-Ville分布相较STFT，具有较好的分辨率，但当信号含有多个成分时，会存在交叉干扰项，引入虚假的能量分布；小波变换则是基于STFT发展起来的，其采用了小波基函数，可以通过伸缩和平移运算对信号进行多尺度细化，可提供一个随频率变化的“时间-频率”窗口，是进行信号时频分析的理想手段。所以本文采用小波变换作为对换能器采集信号进行时频分析的工具。

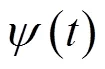
本文采用Morlet函数作为分析小波，其表达式为[15]：

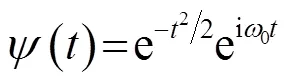
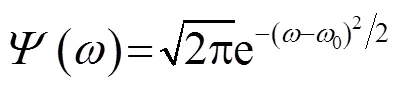
通过Morlet小波变换可得到信号幅值随时间和频率的变化关系。由于文中采用的频率无法满足因材料的非线性引起的二次谐波的条件，故可认为Lamb波在板中传播时，仅存在激励信号的频率成分[16]。则考虑提取激励信号频率0及其附近的多组频率所对应的时域信号，取特定频率时域信号中第一个波峰值为信号传播时间，通过比较健康信号及差信号的信号传播时间，即可确定对应频率下的时间延迟，如图4所示。结合前文计算得到的频散曲线，可计算得到240 kHz频率下的Lamb波相速度p，根据信号传播时间及相速度可计算出损伤到两换能器的距离之和。

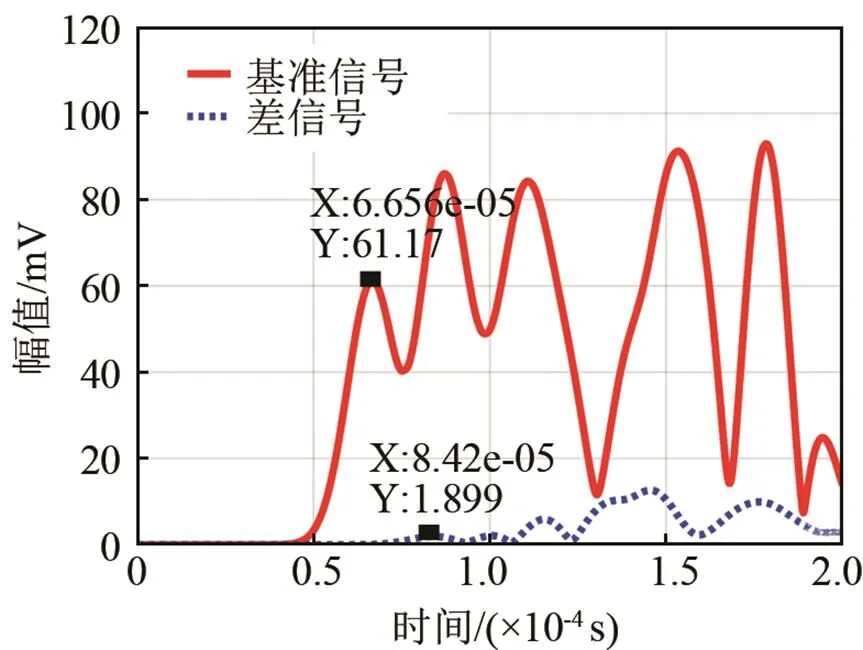
图4 240 kHz频率下的时域信号

3.2 损伤位置的数据融合方法

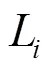
本文采用加权平均法作为数据融合的工具，则有[17]：

其中，为权重值；为融合频率的个数。

因本文采用的激励信号是汉宁窗调制的5个周期正弦信号：

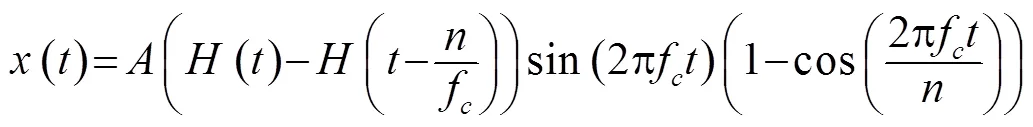
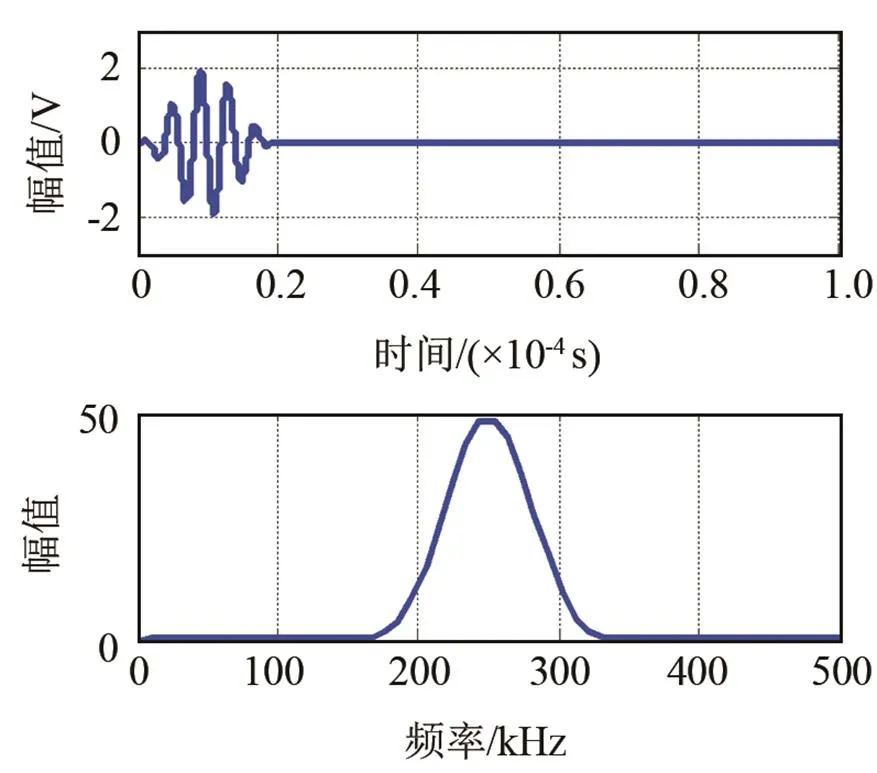
图5 激励信号的时域及频域图

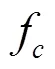
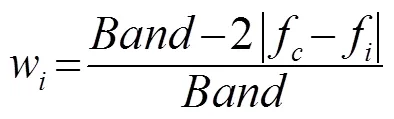
对权值进行归一化处理，得到归一化的权值：

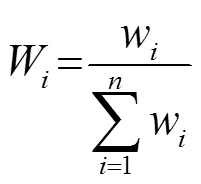
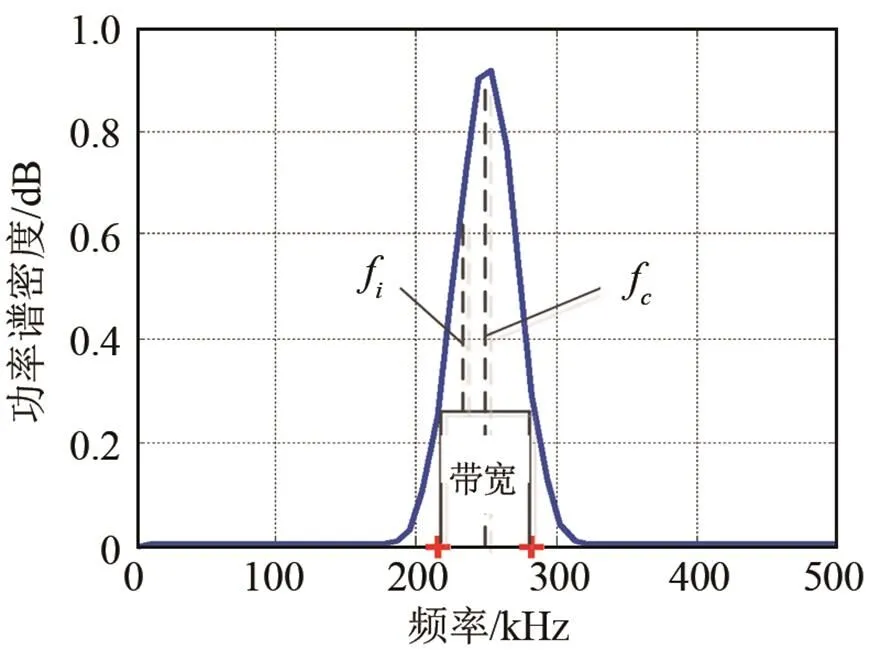
图6 权重确定示意图

得到权值之后，即可依据公式(9)，对所获得的多频率下的损伤到两换能器的距离L进行融合计算，得到可靠性较高的损伤到该组换能器的距离和，并以此法获得其他组的定位信息，进而采用椭圆定位法，即可确定损伤的位置。

4 试验验证

采用尺寸为700 mm×300 mm×3 mm的LY12CZ铝合金薄板为试验对象。通过查材料手册得到该平板的材料参数，并通过计算得到其横波及纵波速度，见表1。试验件示意图见图7。以板的中心位置为零点，横向为轴，纵向为轴，分别在坐标值为(-150，80)、(150，80)，(150，-80)和(-150，-80)位置处粘贴PZT压电片，其中坐标单位为mm，并进行编号。在板(-50，40)位置处，设置直径为5 mm的通孔，作为损伤状态。分别在板健康和损伤状态下进行试验监测。采用NI数字采集设备(Pxi-5105示波器卡、Pix-5412采集卡)，HSA 4052功率放大器，试验设备如图8所示。激励信号为中心频率250 kHz的汉宁窗调制的5周期正弦信号。信号采集频率为1 MHz，信号采集点数为10 000。

表1 材料参数及横纵波速

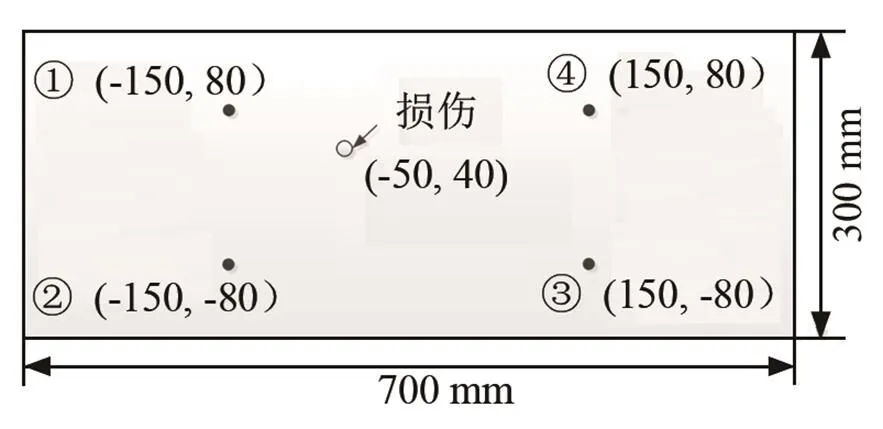
图7 试验件示意图

图8 试验设备

为验证本文方法的优越性，分别由换能器1和2激励，其他换能器接收，分别在健康和损伤状态下获得12组信号，采用信号时域包络法确定时间延迟。以传播路径1-3为例，对信号进行滤波处理以减少噪声影响，得到的健康信号、损伤信号和差信号及其信号包络图如图9所示。

(a) 健康信号

(b) 损伤信号

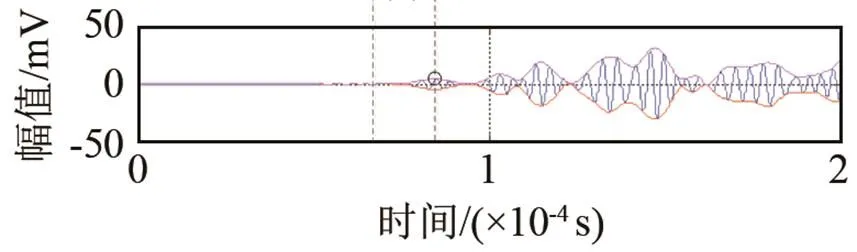
(c) 差信号

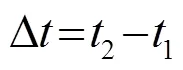
下面采用Morlet小波变换和多频率数据融合的方法对损伤进行椭圆定位。激励信号的中心频率为250 kHz，-3 dB带宽为70 kHz，取230、240、250、260和270 kHz共5组频率作为需要提取的频率。根据公式(12)确定了这5组频率下损伤到换能器对的距离之和的权重，同时根据频散曲线得到了这5组频率下对应的相速度，见表3。

表2 基于信号包络阈值法确定时间延迟

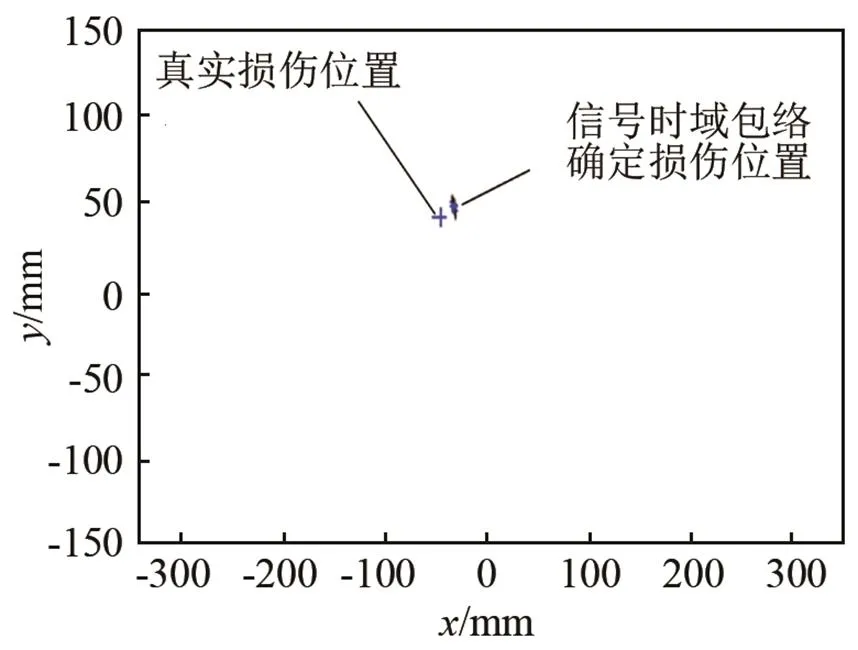
图10 基于时域信号包络阈值法的损伤定位

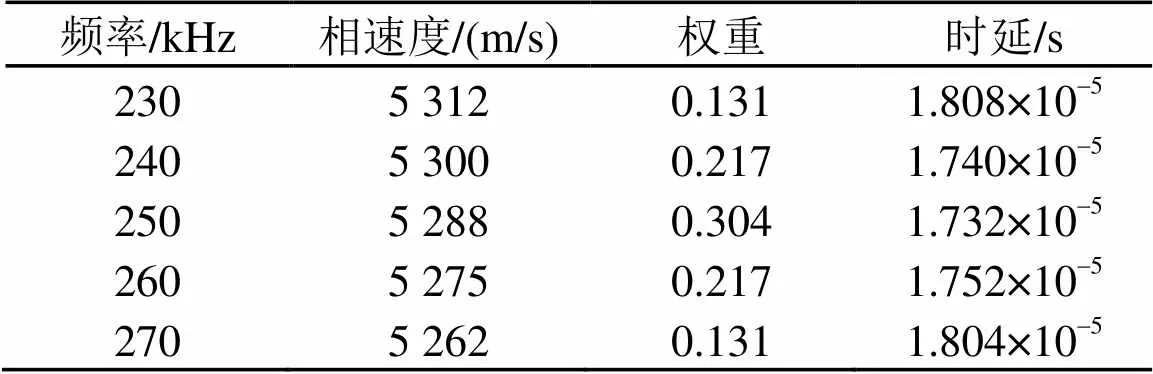
表3 多频率下的相速度、权重值及时间延迟

以换能器路径2-3为例，首先分别对健康信号和差信号进行Morlet小波变换，得到信号的时频图(见图11)，继而分别提取上述5组频率下的时域信号(250 kHz下的时域图见图12)，确定了时间延迟(见表3)，结合权重值，最终确定损伤到换能器2和3的距离之和。

基于本文所提方法，对多条传感路径进行分析，采用多频率下时域信号确定时间延迟，见表4。以此并进行加权平均处理，最终获得多个。采用椭圆定位法进行损伤定位，并成像，经阈值化处理，最终确定损伤位置为(-43.8，43.2)，误差为6.98 mm，如图13所示。

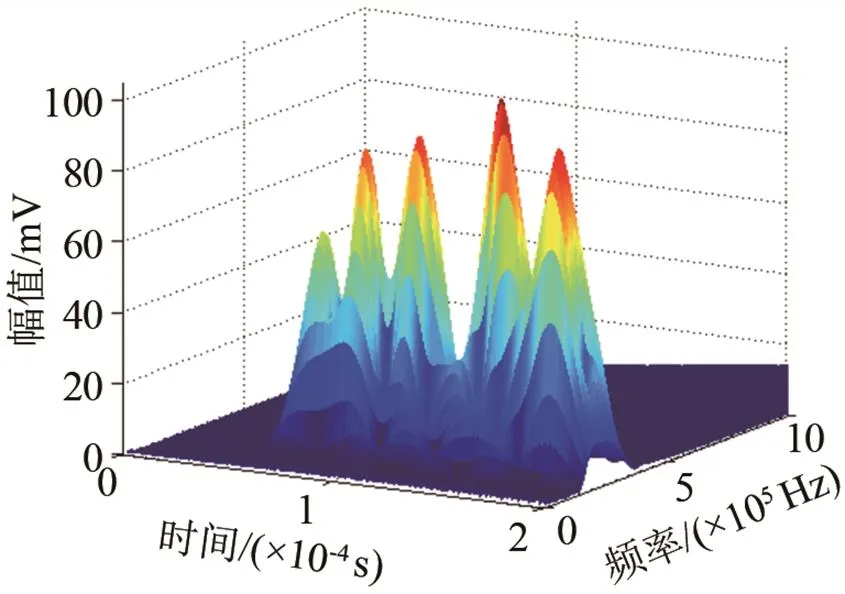
(a) 健康信号小波时频图

(b) 差信号小波时频图

图11 小波时频图

Fig.11 Wavelet time-frequency distribution

图12 250 kHz下时域信号图

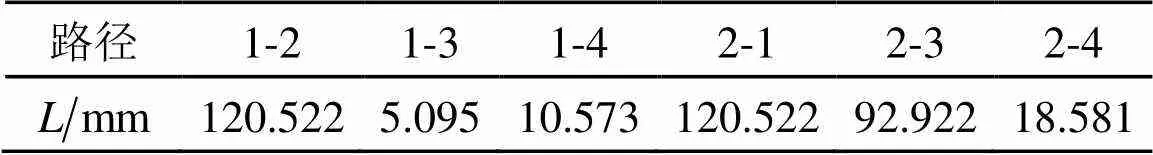
表4 基于小波变换和多频率融合方法获得的路径数据

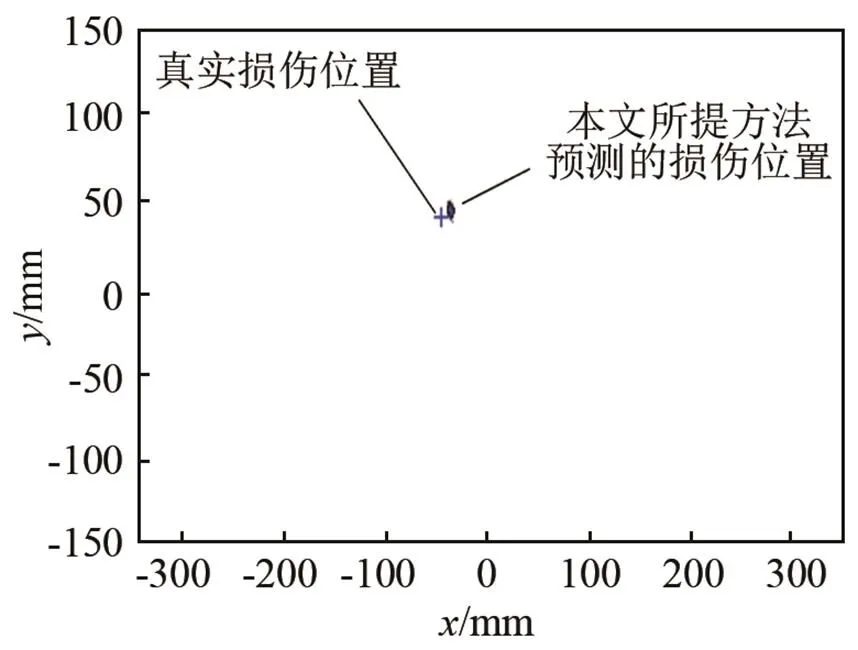
图13 基于Morlet小波变换和多频率数据融合的损伤椭圆定位

5 结论

本文针对Lamb波的频散特性对时间延迟确定的影响，提出了基于小波分析多频率数据融合的椭圆损伤定位方法。该方法基于Morlet小波分析提取了多频率下信号随时间的变化信息，获得了多频率下的时间延迟数据，根据时间延迟数据，对损伤到两换能器的距离之和进行了数据融合，进而基于椭圆定位法进行了损伤定位。通过试验验证，对本文所提方法与常用的信号时域包络法进行了比较。结果表明，该方法可有效避免因Lamb波频散效应引起的时域包络法定位不准的现象，相较信号时域包络法有较好的定位精度，融合了多频率下的传感数据，提高了定位系统的鲁棒性，可减少因系统或人为因素造成的误差。

[1] 袁慎芳. 结构健康监控[M]. 北京: 国防工业出版社，2007. YUAN Shenfang. Structural health monitoring[M]. Beijing: National Defence Industry Press, 2007.

[2] 王强, 袁慎芳, 陈小惠, 等. 主动Lamb波合成波阵面损伤成像监测方法[J]. 仪器仪表学报, 2011, 32(11): 2468-2474. WANG Qiang, YUAN Shenfang, CHEN Xiaohui, et al. Active Lamb wave synthetic wave front damage imaging monitoring method[J]. Chinese Journal of Scientific Instrument, 2011, 32(11): 2468-2474.

[3] 王建强，余龙，张宇, 等. 基于最大相似性的Lamb波损伤信号分解及试验研究[J]. 振动与冲击, 2014, 33(24): 200-204. WANG Jianqiang, YU Long, ZHANG Yu, et al. Damage signal decomposition of Lamb wave and tests based on similarity[J]. Journal of Vibration and Shock, 2014, 33(24): 200-204.

[4] Alessandro Perelli, Luca De Marchi, Alessandro Marzani, et al. Frequency warped cross-wavelet multi-resolution analysis of guided waves for impact localization[J]. Signal Processing, 2014, 96(5): 51-56.

[5] Ben B S, Ben B A, Vikramb K A, et al. Damage identification in composite materials using ultrasonic based Lamb wave method[J]. Measurement, 2013, 46(2): 904-912.

[6] 刘增华, 徐营赞, 何存富, 等. 板状结构中基于Lamb波单模态的缺陷成像试验研究[J]. 工程力学, 2014, 31(4): 232-238. LIU Zenghua, XUE Yingzan, HE Cunfu. experimental study on defect imaging based on single Lamb wave mode in plate-like structures[J]. Engineering Mechanics, 2014, 31(4): 232-238.

[7] 徐颖娣, 袁慎芳, 彭鸽. 二维结构损伤的主动Lamb波定位技术研究[J]. 航空学报, 2004, 25(5): 446-479. XU Yingdi, YUAN Shenfang, PENG Ge. Study on two- dimensional damage location in structure based on active Lamb wave detection technique[J]. Acta Aeronautica Et Astronautica Sinica. 2004, 25(5): 446-479.

[8] 于勇凌, 张海燕, 冯国瑞, 等. 兰姆波检测信号的匹配追踪时频分析[J]. 声学学报, 2013, 38(5): 576-582. YU Yongling, ZHANG Haiyan, FENG Guorui, et al. Matching pursuit time-frequency analysis of Lamb wave detection signals[J]. Acta Acustica, 2013, 38(5): 576-582.

[9] Fenza A D, Sorrentino A, Vitiello P. Application of Artificial Neural Networks and Probability Ellipse methods for damage detection using Lamb waves[J]. Composite Structures, 2015, 133: 390-403.

[10] Pai P F, Deng H, Sundaresan M J. Time- frequency characterization of Lamb waves for material evaluation and damage inspection of plates[J]. Mechanical Systems and Signal Processing(S 0888-3270), 2015, 62-63: 183-206.

[11] GE Luyao, WANG Xinwei, JIN Chunhua. Numerical modeling of PZT-induced Lamb wave-based crack detection in plate-like structures[J]. Wave Motion(S 0165-2125), 2014, 51(6): 867-885.

[12] 彭鸽, 袁慎芳, 徐颖娣. 基于主动Lamb波和小波变换的二维结构损伤定位研究[J]. 振动工程学报, 2004, 17(4): 488-493. PENG Ge, YUAN Shenfang, XU Yingdi. Damage location of two-dimensional structure based on wavelet transform and active monitoring technology of lamb waves[J]. Journal of Vibration Engineering, 2004, 17(4): 488-493.

[13] LU Y, YE L, WANG D, et al. Conjunctive and compromised data fusion schemes for identification of multiple notches in an aluminium plate using Lamb wave signals.[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control(S 0885-3010), 2010, 57(9): 2005-2016.

[14] 严宏, 周丽. 基于损伤存在概率成像方法的复合材料结构损伤识别[J]. 振动与冲击, 2012, 31(13): 76-80. YAN Hong, ZHOU Li. Damage identification of composite structures based on reconstruction algorithm for probabilistic inspection of damage[J]. Journal of Vibration and Shock, 2012, 31(13): 76-80.

[15] Boggess Albert, Narcowich Francis J. 小波与傅里叶分析基础[M]. 北京: 电子工业出版社, 2013. Boggess Albert, Narcowich Francis J. Wavelets with Fourier analysis[M]. Beijing: Publishing House of Electronics Industry, 2013.

[16] 邓明晰, Price D C, Scott D A. 兰姆波非线性效应的实验观察[J]. 声学学报, 2005, 31(1): 1-7. DENG Mingxi, D.C.Price, D.A.Scott. experimental observation of nonlinear effects of Lamb waves[J]. Acta Acustica, 2005, 31(1): 1-7.

[17] 刘同明, 夏祖勋, 解洪成. 数据融合技术及应用[M]. 北京: 国防工业出版社, 1998: 1-12.LIU Tongming, XIA Zuxun, XIE Hongcheng. Data fusion technology and its application[M]. Beijing: National Defense Industry Press, 1998.

Research on multi-frequency data fusion based Lamb wave damage localization

YANG Xiao-hua1, LIU Xue-jun1, MA Guang-ting2

(1. Department of Aviation Mechanism, Qingdao Branch, Naval Aeronautical and Astronautical University, Qingdao 266041, Shandong, China;2. Unit 91899 of PLA, Huludao 125001, Liaoning, China)

Determination of damage location is an important part of structural health monitoring, and time delay is the key parameter to determine the damage location. A damage localization method based on Morlet wavelet transform and data fusion is put forward to reduce the influence of Lamb wave dispersion on the localization accuracy. Travel time information at several special frequencies is extracted, so the signal arrival time is determined. The distance of damage to sensors is obtained based on weighted processing. Damage localization is determined based on ellipse localization method. Simulation results show that the method can reduce the influence of dispersion effect, improve the accuracy of localization and enhance the system anti-interference ability.

Lamb waves; Morlet wavelet; ellipse localization method; data fusion; time delay

V214.8 TB332

A

1000-3630(2017)-02-0133-07

10.16300/j.cnki.1000-3630.2017.02.007

2016-05-20;

2016-08-13

总装预研项目(143092015)

杨晓华(1964－), 男, 江苏启东人, 博士, 教授, 博士生导师, 研究方向为飞机结构寿命评定。

刘学君, E-mail: liuxuejun_2007@163.com