三种双扫描横波分裂算法在裂缝探测中的应用研究

张建利 王 赟 刘志斌 李绪宣

（①中海油研究总院，北京100027；②中国科学院地质与地球物理研究所，北京100029；③中国地质大学（北京）地球物理与信息技术学院，北京100083）

三种双扫描横波分裂算法在裂缝探测中的应用研究

张建利*①②王 赟③刘志斌①李绪宣①

（①中海油研究总院，北京100027；②中国科学院地质与地球物理研究所，北京100029；③中国地质大学（北京）地球物理与信息技术学院，北京100083）

为了准确利用横波分裂方法探测裂缝，将天然地震资料处理常用的双扫描算法应用到转换波勘探，有必要对其适用条件和反演精度进行研究。从横波分裂基本性质出发，首先归纳了双扫描算法的流程；然后以含裂缝地层模型为例，测试了切向能量法、旋转相关法和协方差矩阵法三种双扫描算法在不同条件下的反演精度和鲁棒性；最后将其应用到西部M工区致密含气砂岩储层的裂缝探测，并与传统能量比值法进行了对比。结果表明：①当炮检方位与裂缝发育方位间隔一定角度时，三种双扫描算法都能得到准确结果；②与另外两种方法相比，切向能量法更加稳定，可以应用到炮检方位接近裂缝发育方位的特殊情况；③炮检距对双扫描算法存在一定影响，炮检距增大时误差也随之增大。

横波分裂 裂缝探测 双扫描 致密含气砂岩

1 引言

横波传播到各向异性介质界面会产生横波分裂现象，横波分裂的两个参数快波偏振方位和快慢波分裂时差分别反映了裂缝发育方位和发育密度。自20世纪70年代发现横波分裂现象以来，横波分裂参数反演一直是横波分裂研究的重点和难点。20世纪90年代之前，主要应用多分量VSP资料进行人工源横波分裂测量，先后发展了Alford张量旋转法［1］、传递函数法［2，3］、剥层法［4］、双源累积技术［5］、线性变换技术［6］等反演方法。同一时期，为了利用天然横波资料对地球深部横向结构进行探测，先后发展了旋转相关法［7，8］、切向能量法［9，10］、协方差矩阵法［11］等双扫描算法，即同时对两个参数网格扫描以确定最优解，既能用于多方位资料反演，又能用于单方位资料反演。2000年以后，转换波勘探成为多分量勘探的主要形式，相对于VSP观测的“点”特性，转换波分裂反演可提供裂缝分布的“面”预测而更具优势［12］。近年来，为了准确地从转换波资料反演横波分裂参数，地球物理工作者一方面对能量比值法等传统方法进行改进［13-15］，另一方面把双扫描算法引入到转换波资料处理［16-19］，扩展了横波分裂反演的适用范围，并取得了良好效果。

无论是传统能量比值法还是双扫描算法，都是利用横波分裂的基本性质进行反演。在地球响应为线性的假设下，横波分裂的基本性质包括：①转换横波初始偏振呈线性；②转换横波初始偏振沿径向；③快、慢波波形相似。利用三种基本性质，分别发展了协方差矩阵法、切向能量法和旋转相关法三种最基本的双扫描算法。因此，在将三种双扫描算法应用于转换波资料处理之前，有必要对其适用范围和反演精度以及稳定性进行分析。

本文从横波分裂基本性质出发，首先归纳了三种双扫描算法的基本原理和处理流程；然后对含裂缝地层模拟了不同测量方位下的二维三分量地震记录，以此为基础，分别测试了理想情况下和加噪情况下三种算法在不同测量方位和炮检距时的表现；最后将三种算法应用到西部M工区致密砂岩气储层的裂缝探测，并与传统能量比值法进行了对比。

2 双扫描算法原理

横波分裂反演是其正演的反过程。在转换波垂直出射并且初始偏振沿径向的假设下，首先推导水平接收分量和快慢波分量之间的转换关系式。在野外一般沿测线方向X和垂直于测线方向Y进行观测，根据横波偏振特性，后续处理前需要旋转到炮—检连线方向（径向R）和与之正交的方向（切向T）。为表述方便，公式推导和模型正演时都设定检波器的两个水平分量分别沿径向和切向记录。

根据横波分裂原理，当初始线性偏振的转换波S传播到EDA介质［20］（Extensive Dilatancy Anisotropy，即具有水平对称轴的广泛扩容各向异性介质）时，会分裂为传播速度不同的快、慢横波，其中快波S1沿优势方位偏振，慢波S2沿对称轴方位偏振［21］；在转换波初始偏振沿径向的前提下，该过程可以表示为

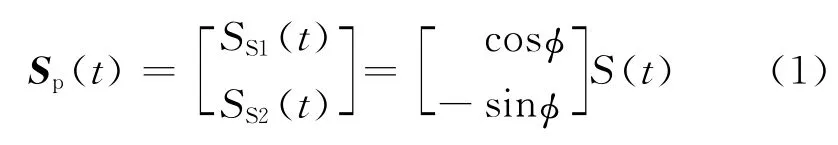
式中：S为转换波的初始波形；Sp为其传播矢量，此时快、慢波时差为0。这一过程也可以在图1中的水平坐标系中表示。

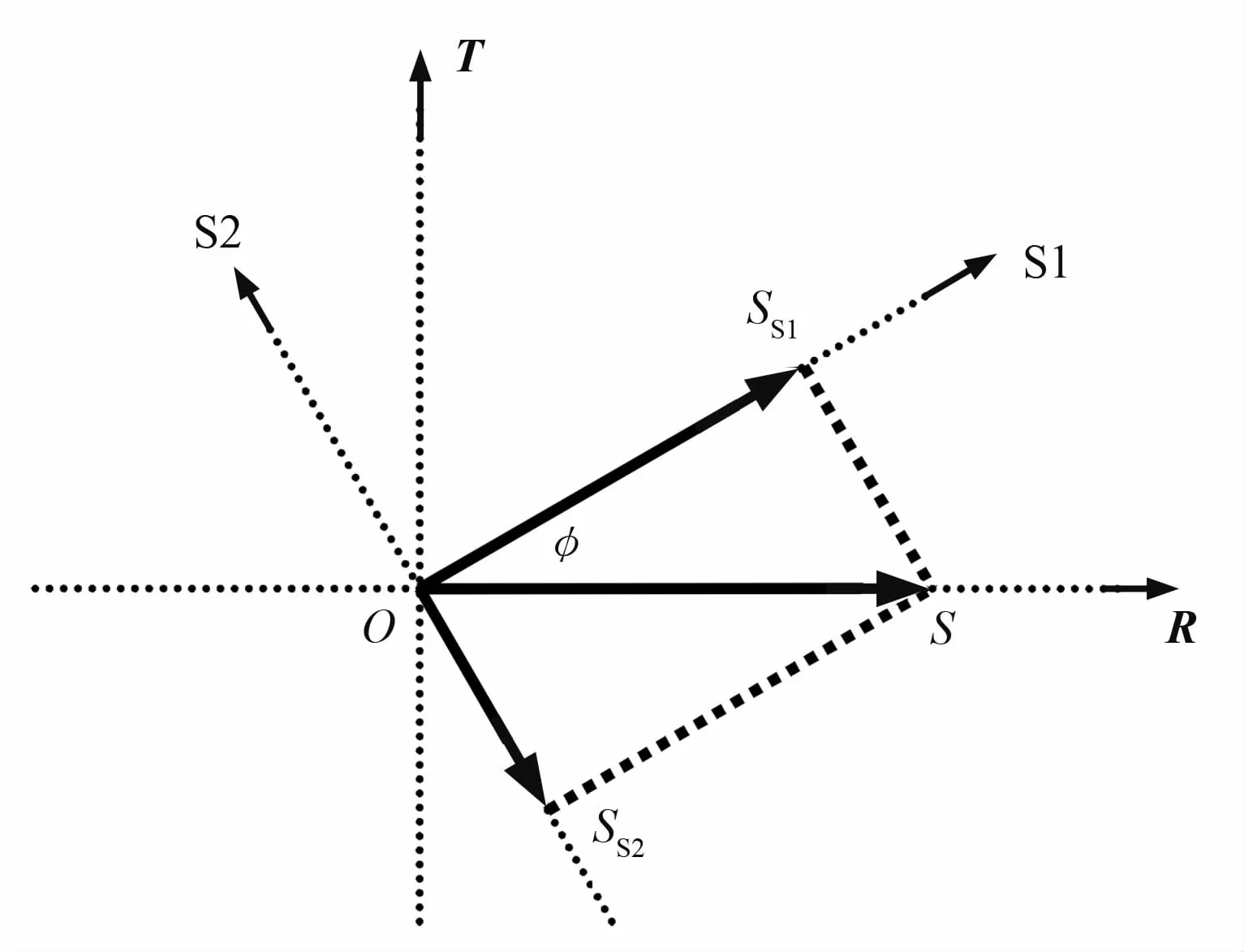
图1 横波分裂过程在水平坐标系内的表示

快、慢波在方位各向异性介质中传播一段距离后会产生时差。基于矢量褶积思想，传播到检波点的快、慢横波组成的传播矢量dp（t）可以表示为

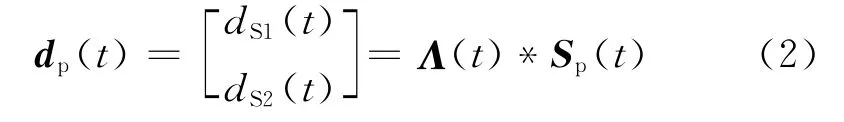
式中：dS1（t）和dS2（t）分别表示检波点记录到的快、慢横波；星号“*”表示时域内的褶积；算子Λ（t）的表达式为

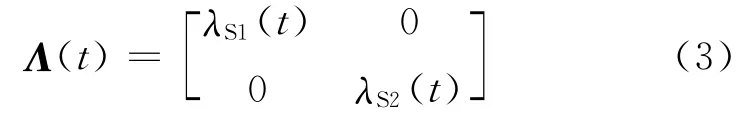
在时域内，λS1（t）、λS2（t）分别与初始转换波形S（t）褶积产生快、慢波分裂的振幅和时延，即

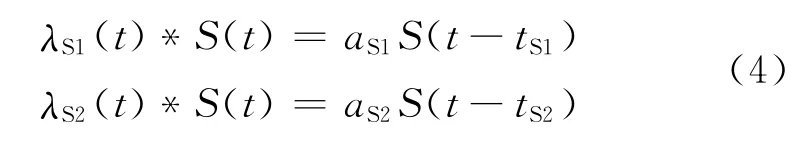
式中：tS1和tS2分别表示快、慢横波的旅行到时；aS1、aS2分别是快、慢波的振幅。

根据图1中的坐标转换关系，将传播矢量dp（t）从自然坐标系旋转到运算坐标系R-T，可以得到运算分量和快慢波分量之间的基本关系式

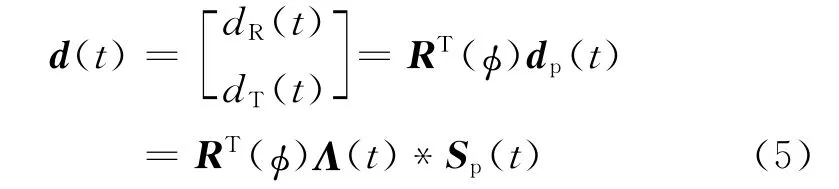
式中：dR（t）和dT（t）分别表示观测到的径向和切向分量，旋转矩阵R（φ）为

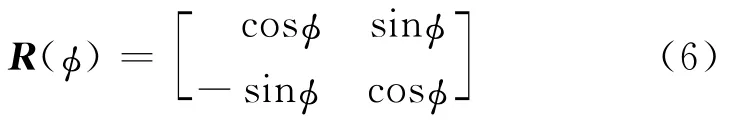
双扫描算法对转换波资料反演横波分裂的一般流程如下。

（1）将径向、切向分量旋转到假设的快、慢波偏振方位

对旋转角度φx进行扫描，当φx=φ，即旋转到正确的快、慢波偏振方位时，快、慢波完全分离，即

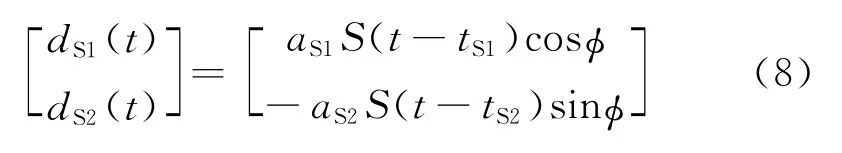
（2）采用假设的分裂时差δt x对慢波分量进行时延补偿

对分裂时差进行扫描，当δt x=tS2-tS1时，补偿时延后的快、慢波到时一致，由横波分裂形成的方位各向异性效应完全消除。这是据旋转相关法的基本原理，快、慢波波形相似，此时快、慢波分量的相关系数最高；同时，快、慢波合成矢量的偏振轨迹将从椭圆回归为线性，所以快、慢波协方差矩阵的特征值将取得最小值，这就是协方差矩阵法的基本原理。

（3）如果将准确补偿时延后的快、慢波分量旋回R-T坐标系，可得

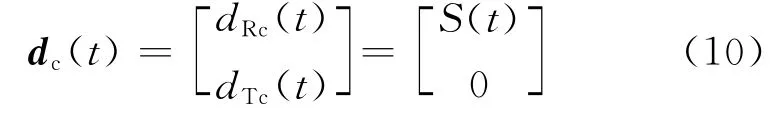
式中dRc（t）和dTc（t）为补偿方位各向异性后的径向和切向分量。由于转换波初始偏振沿径向，此时切向分量上转换波能量应取得最小值，这就是切向能量法的基本原理。

因此，双扫描算法就是根据横波分裂的不同性质建立不同的目标函数，对快波偏振方位和快慢波分裂时差同时网格扫描以获取最优解的方法。旋转相关法的目标函数可以表示为

式中：dS1x、dS2x是将径向和切向分量旋转到假设的快波偏振方位φx及其垂向，并补偿时延δt x得到的快、慢波分量；分别为dS1x、dS2x的平均值。对φx和δt x同时进行扫描，当目标函数（相关系数）取得最大值时，扫描参数即为所求。

设D是dS1x和dS2x两分量的协方差矩阵，则协方差矩阵法的目标函数可以表示为

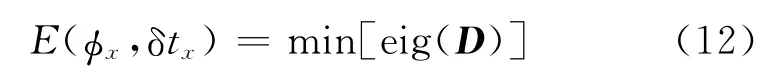
式中eig（·）表示求特征值操作，且

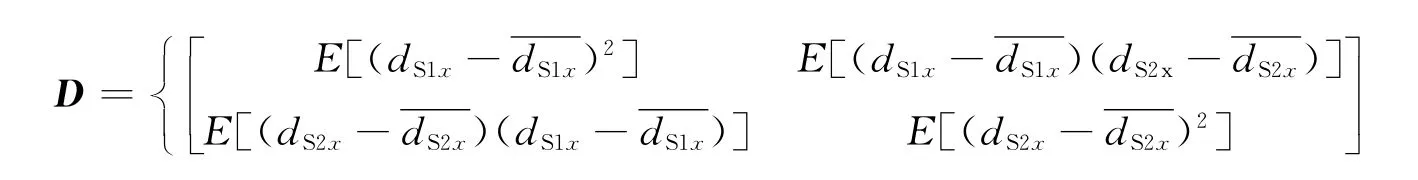
当目标函数（协方差矩阵特征值）取得最小值时，扫描参数即为所求。

类似地，可以得到切向能量法的目标函数为

绝大部分ncRNA不编码蛋白质，在RNA水平上发挥其生理功能.越来越多的研究表明原核生物体内存在的转录后调控与ncRNA密切相关.ncRNA的功能多种多样，几乎参与了细菌的各个生命活动过程.针对S. Typhi中发现的ncRNA AsrC，对其表达特性和功能进行初步研究.

式中dTcx表示将dS1x和dS2x旋回R-T坐标系得到的切向分量。当扫描得到最小切向能量时，相应的扫描参数即为所求，而径向和切向的方位各向异性得到了剥除。

3 模型测试

设计一个单反射界面模型以测试三种双扫描算法的适用范围和稳定性。模型上层为Hudson型裂缝层，背景介质纵波速度为2400m／s，横波速度为1200m／s，密度为2000kg／m3，层厚为800m，裂缝密度为0.01；下层为各向同性地层，纵波速度为2500m／s，横波速度为 1300m／s，密度为 2100kg／m3，层厚300m。根据上述设定，可计算得到垂直出射的快、慢横波时差约为14ms。

在与裂缝方位夹角为0°、15°、30°、45°、60°、75°的方位分别布置测线，如图2所示。采用左侧放炮、右侧50个检波器接收的单边观测方式，模拟各方位测线的二维三分量记录。其中，震源类型为胀缩震源，激发Ricker子波；最小炮检距为100m，道间距为20m，时间采样间隔为1ms，最大记录时长为1.5s。图3展示了45°方位测线的三分量记录，可以看到，由于存在横波分裂，T分量剖面有显著的转换波，而且由快、慢波叠加形成的同相轴呈现“双峰”形态，区别于Ricker子波的“单峰”形态。

对所有方位测线所有炮检距的地震道截取转换波所在时窗，分别采用三种双扫描算法反演各道的快波偏振方位和快慢波时差，并计算测量值和理论值的绝对误差，结果如图4所示。其中，快波偏振方向的扫描范围是-90°～+90°，扫描间隔为1°；快慢波时延的扫描范围是0～40ms，扫描间隔为1ms。

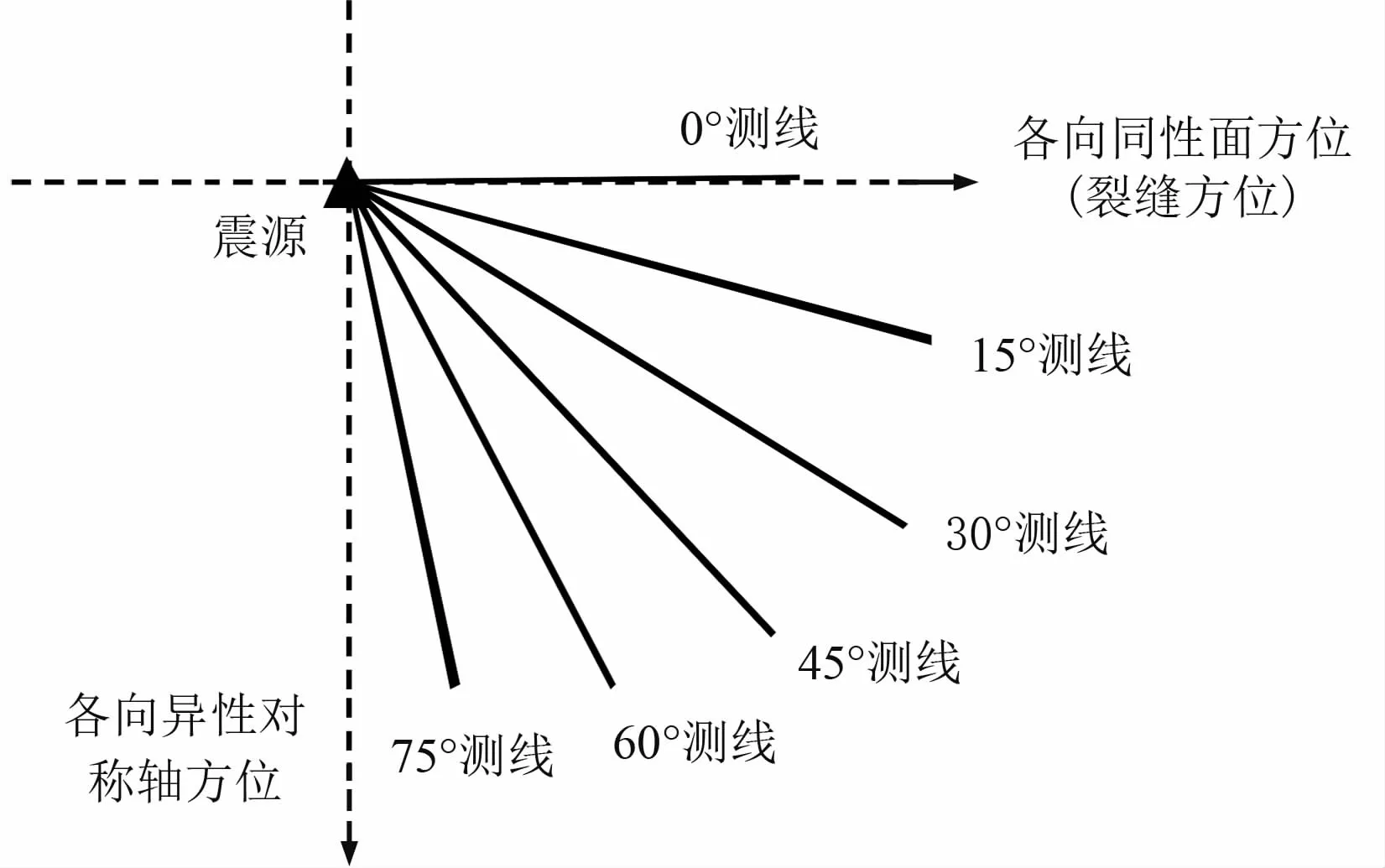
图2 水平面内二维测线的方位分布

图3 45°方位测线的三分量地震记录

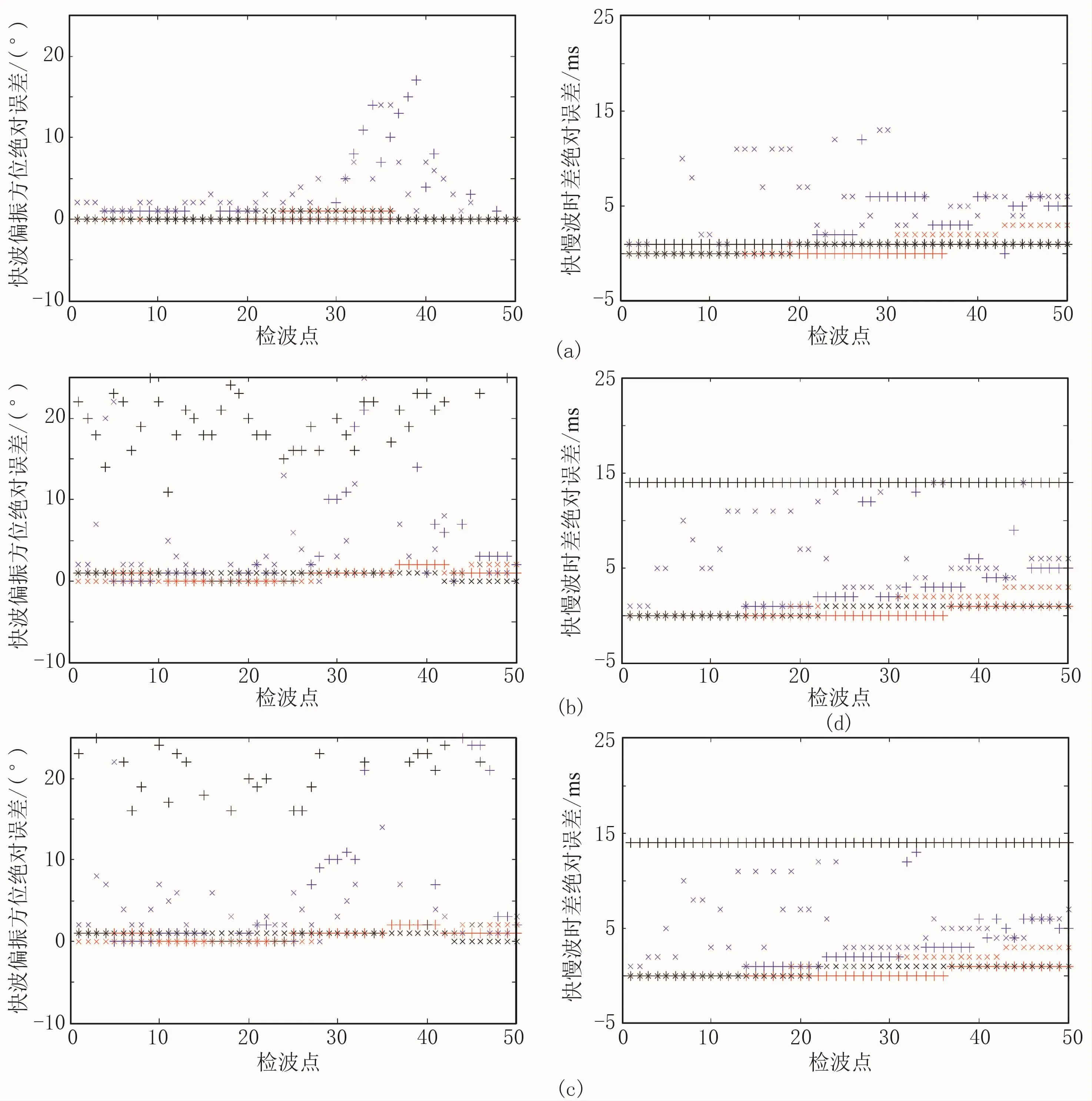
图4 三种双扫描算法对6条方位测线反演的快波偏振方位（左）和快慢波时差（右）的绝对误差

图4结果都是在无噪声的理想条件下扫描得到，而野外资料都是含噪声的，有必要进一步研究含噪声时三种算法的表现。设定信噪比SNR分别为5和2，向原始记录中添加符合标准正态分布的随机噪声。针对与裂缝方位夹角分别为15°和45°的两条测线开展试验，以表征靠近和远离裂缝方位的两种极端情况。为了使测试结果具有统计意义且更加直观，对两条测线的每一道数据都添加随机噪声，然后采用三种双扫描算法反演，并计算测量值与理论值的绝对误差，如此重复测试50次，将绝对误差以散点的形式绘制在图上。协方差矩阵法结果放在底层，覆之以旋转相关法结果，最后将切向能量法结果放在顶层。图5展示了信噪比为5时，三种双扫描算法对15°方位测线进行50次随机试验的结果，相应地，图6展示了信噪比为2时的实验结果；图7展示了信噪比为5时，三种双扫描算法对45°方位测线进行50次随机试验的结果，图8展示了信噪比为2时的结果。

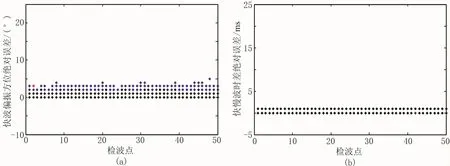
图5 当信噪比为5时的15°方位测线三种双扫描算法50次随机试验散点图

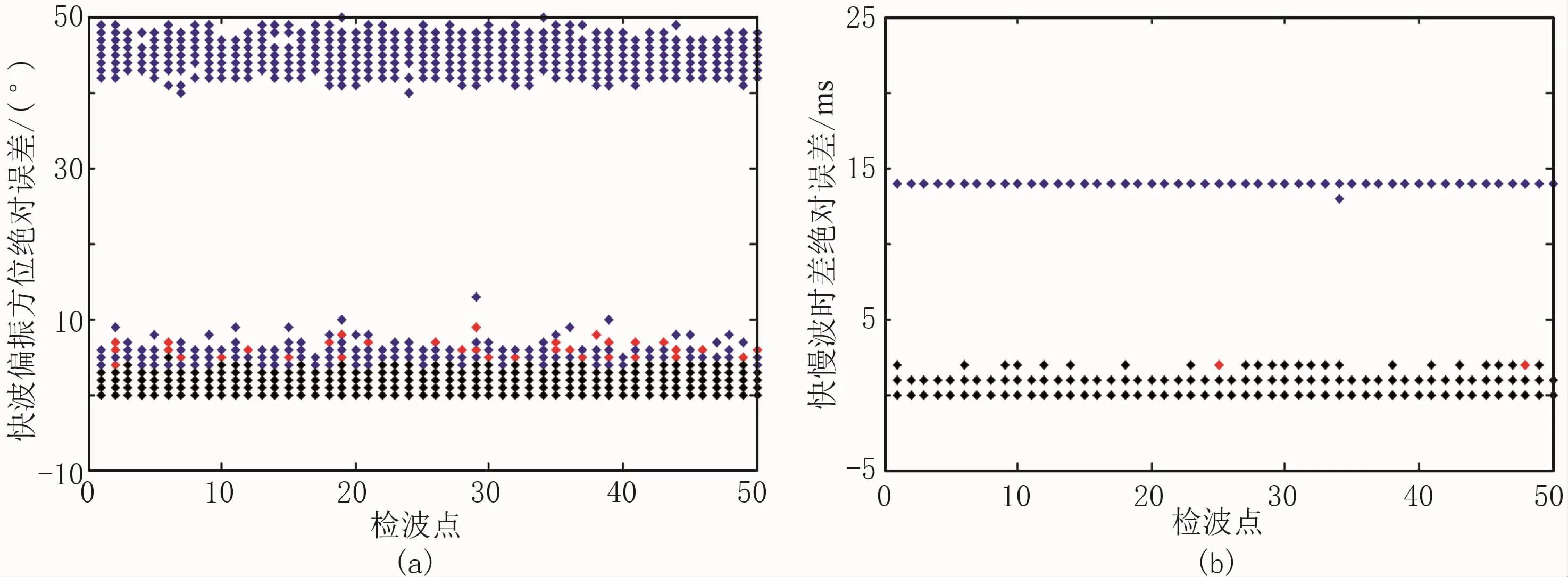
图6 当信噪比为2时的15°方位测线三种双扫描算法50次随机试验散点图

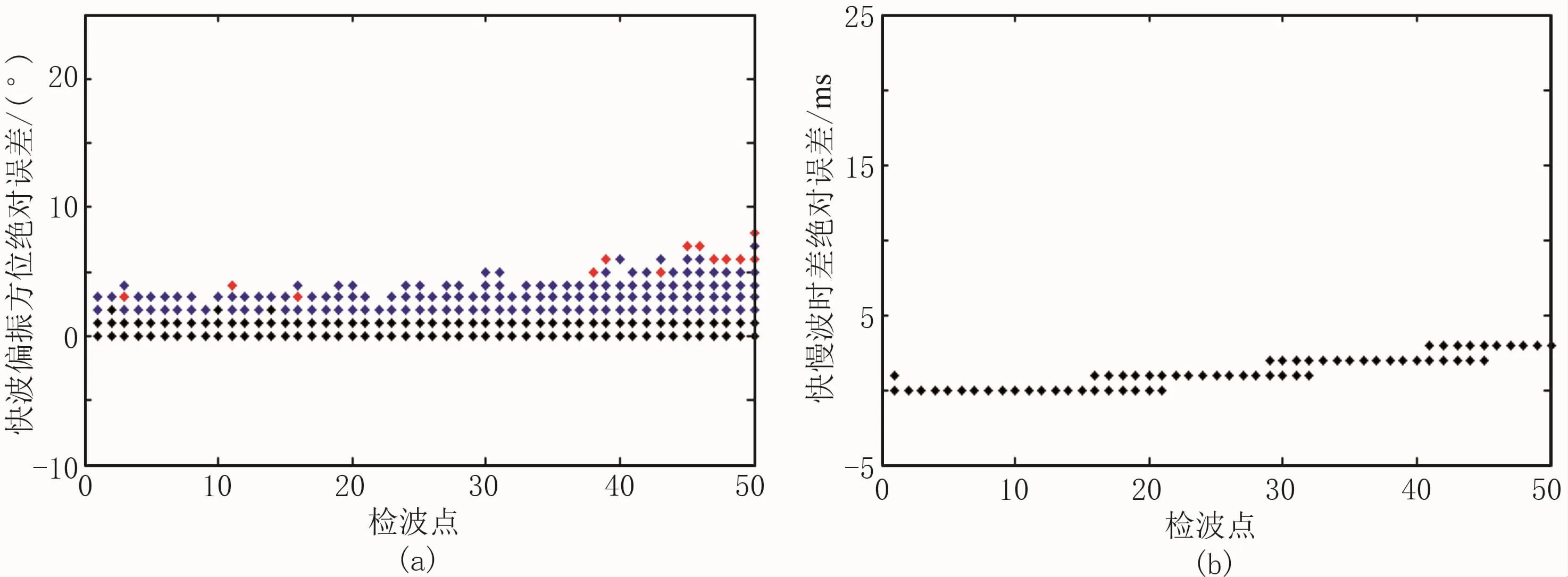
图7 当信噪比为5时的45°方位测线三种双扫描算法50次随机试验散点图

图8 当信噪比为2时的45°方位测线三种双扫描算法50次随机试验散点图

对模型测试结果进行分析，可得如下认识。

（1）双扫描算法会受到水平面内测线与裂缝相对方位的影响。当测线方位远离裂缝方位或其垂向时，三种算法反演准确；当测线靠近裂缝方位或其垂向时，切向能量法反演精度最高，协方差矩阵法稍差，旋转相关法偏差较大；这是因为当观测方位靠近裂缝方位或其垂向时，快、慢波相似这一特性容易被噪声破坏。

（2）双扫描算法会受到炮检距的影响。随着炮检距的增大，反演误差也随之增大；这是因为炮检距较大时，转换波不再满足垂直出射的条件，快、慢横波偏振方向在水平面的投影不再正交。

（3）在鲁棒性方面，当观测方位远离裂缝方位时，三种双扫描算法都比较可靠，而且切向能量法精度最高；当观测方位靠近裂缝方位时，切向能量法和协方差矩阵法抗噪性好，旋转相关法误差很大。

在设置模型参数时，分别将快慢波时差设置为子波周期的仍然可以得到上述定性认识，表明上述结论具有一般性。

4 应用实例

实际地下构造比上述单界面模型复杂得多，地震资料也更加难以处理，因此有必要测试三种双扫描算法对实际资料的处理效果。采用三种双扫描算法对西部M工区致密含气砂岩储层的一个全方位共检波点道集进行处理，并与传统能量比值法进行对比，以检验上述定性认识是否准确。

野外观测时如图9a所示布置观测系统，以检波点为中心共激发73炮，炮点相对于检波点的实际方位分布如图9b所示。从图中可见，炮点方位间隔约为5°，并形成全方位覆盖，可以满足靠近和远离裂缝方位的测试条件。

预处理后的径向和切向分量共检波点道集如图10a、图10c所示。可以看到，在1.0～1.4s时间窗口内，径向分量同相轴存在显著的“双曲”现象，切向分量同相轴存在以90°为周期的“极性反转”现象，这是地层方位各向异性及横波分裂存在的标志，经过方位各向异性补偿后，“双曲”和“极性反转”现象消失，径向同相轴恢复平直、连续，切向分量上转换波能量被剥离，其本质是由快、慢横波的振幅比随方位周期性变化引起［22］。

图9 野外实验观测系统（a）和炮点方位平面分布（b）

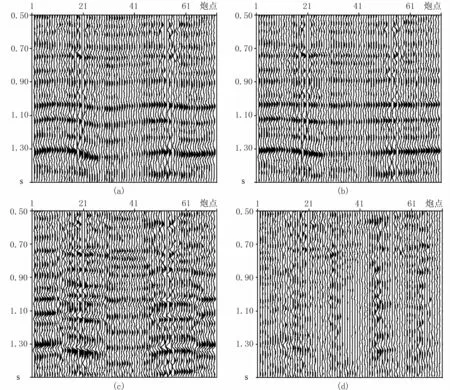
图10 原始径向（a）和切向（b）分量以及经过方位各向异性补偿的径向（c）和切向（d）分量共检波点道集

首先采用传统能量比值法，在第一层同相轴1.0～1.2s时窗内，计算各地震道的径向与切向转换波振幅比，并对所有地震道的测量值进行曲线拟合，结果如图11所示。可以看到，拟合曲线呈现接近180°的周期变化，符合单组方位各向异性的特征［23，24］。根据传统能量比值法的基本原理，当炮—检方位（即径向）与裂缝发育方位平行时，径／切向振幅比将取得最大值，由此可以判断，检波点指向第10炮的方位最接近裂缝发育方位。

然后采用三种双扫描算法对时窗的每一道数据进行反演。其中，快波偏振方向扫描间隔为1°，快慢波时差扫描间隔为2ms，获得的各道快波偏振方向和快慢波时差如图12所示。为了与传统能量比值法进行对比，假定能量比值法计算的第10炮方位即裂缝发育方位，根据图9b中的炮点相对方位关系求得各炮点相对裂缝方位（快波偏振方位）参考曲线，并通过相关计算能量比值法得到的各道分裂时差参考曲线。从图中可以获得以下认识。

（1）三种算法反演的快波偏振方位与能量比值法所求参考值的误差一般小于10°，而分裂时差都在15～25ms区间，说明若以能量比值法的测量结果为参考值，三种双扫描算法是较可靠的，而且与只能用于多方位资料的能量比值法不同，双扫描算法既可以用于多方位资料，也可以用于单方位资料。

（2）与另两种算法相比，切向能量法反演误差最小；当炮检方位远离裂缝方位时，三种算法都反演准确；当炮检方位靠近裂缝方位时，切向能量法仍然能得到准确结果，另两种算法表现较差，尤其是旋转相关法误差较大，这与模型测试得到的认识一致，表明上述定性认识具有一般性和实际意义。

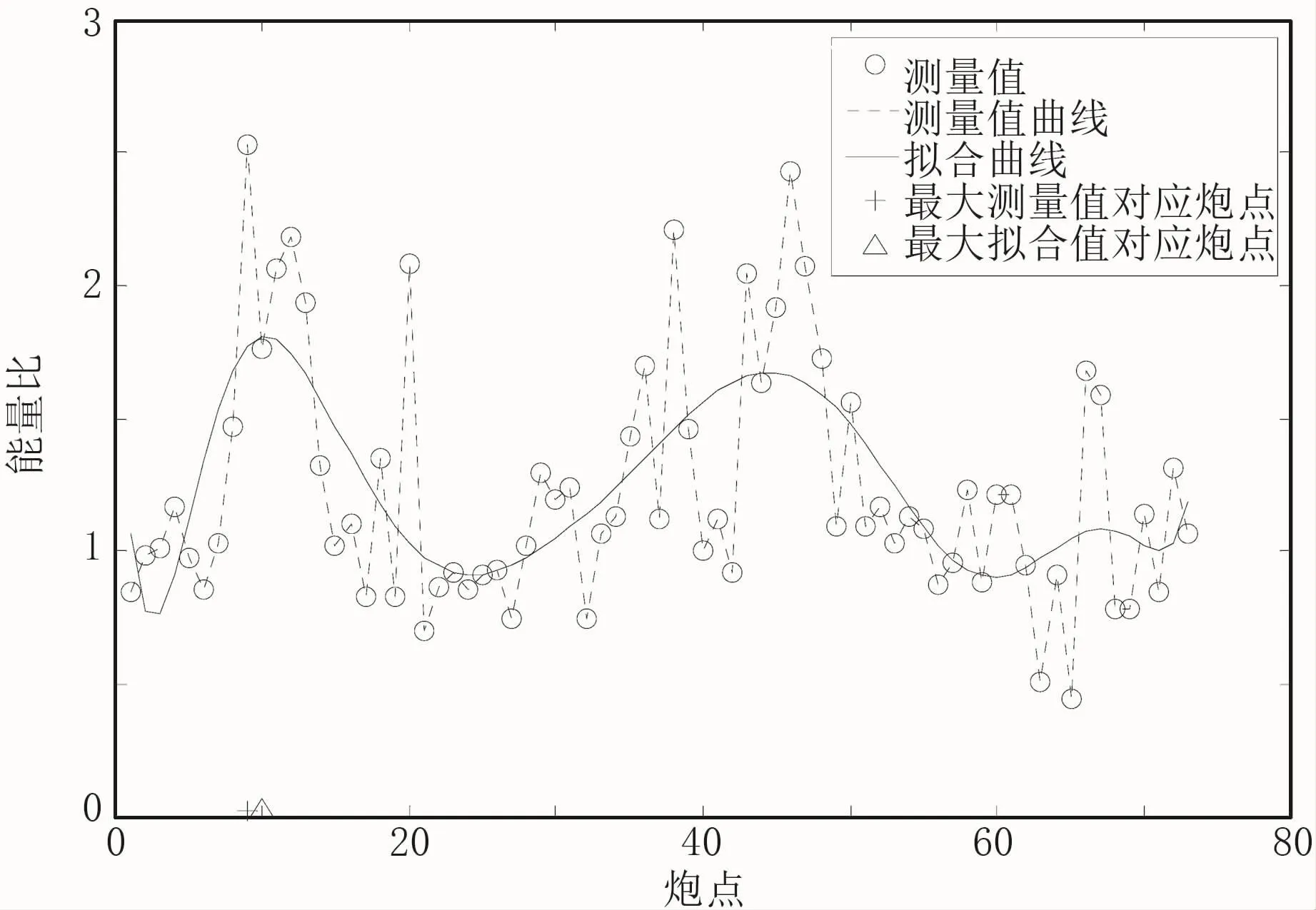
图11 共检波点道集各炮径／切向振幅比测量值及其拟合曲线

（3）协方差矩阵法和旋转相关法的反演结果有很多重合，这是因为协方差矩阵法一定程度上也利用了波形相似这一特征。

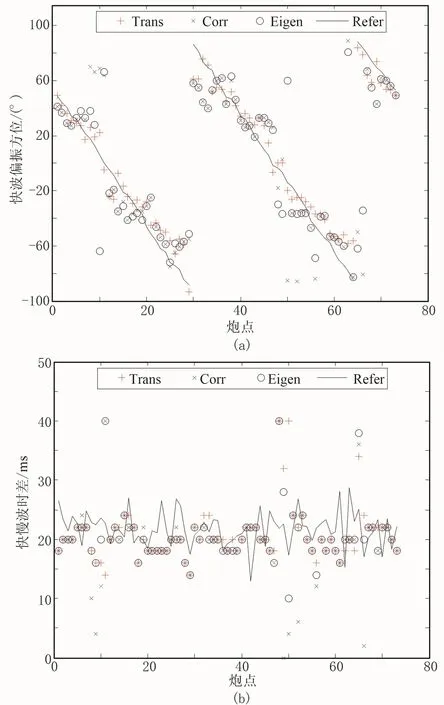
图12 三种双扫描法对各道反演得到的快波偏振方位（a）及快慢波时差（b）

当得到快波偏振方位和快慢波时差以后，根据横波分裂反过程，可以对时窗内层位以及下伏所有层位进行方位各向异性补偿。由于一般有多层裂缝介质，所以通常采用自上而下逐层反演横波分裂、并补偿方位各向异性的层剥离法处理［14］。尝试采用切向能量法反演结果，对时窗内层位以及下伏所有层位进行计算，得到补偿后的径向和切向分量，如图10b、图10d所示。可以看到，径向剖面1.0s以下所有层位同相轴被拉平，切向剖面上转换波被剥离。根据层剥离的原理，继续对1.2～1.4s时窗反演横波做分裂处理，没有得到有效的分裂参数，这表明1.0～1.2s时窗内的层位是惟一主要方位各向异性介质［25］。与补偿前相比，补偿后径向上的“双曲”和切向上的“极性反转”现象消失，径向上同相轴的连续性显著提高，因此如果在偏移前先剥离方位各向异性，可以显著提高偏移成像的分辨率［13］。

5 结论与认识

（1）当炮检方位与裂缝方位在水平面内有一定角度时，三种双扫描算法都相当可靠，而且不仅可用于多方位资料反演，也可用于单方位资料反演，扩展了横波分裂的应用范围。

（2）与另外两种方法相比，切向能量法最为稳定，不仅反演精度更高，而且在炮检方位接近裂缝方位时也能得到准确结果，协方差矩阵法和旋转相关法在此情况下反演误差较大。

（3）双扫描算法会受到炮检距的影响，炮检距增大时误差也随之增大，这是因为炮检距较大时，快、慢横波偏振在水平面上的投影不再正交，这一点还需要进一步研究。

上述认识可为横波分裂探测裂缝的资料采集和处理提供一定的指导。

［1］ Alford，R.Shear data in the presence of azimuthal anisotropy.SEG Technical Program Expanded Abstracts，1986，5：476-479.

［2］ Lefeuvre F，Winterstein D，Meadows M et al.Propagator matrix and layer stripping methods：A comparison of shear-wave birefringence detection on two data sets from railroad gap and Lost Hills Fields.SEG Technical Program Expanded Abstracts，1991，10：55-61.

［3］ Nicoietis L，Client C，Lefeuvre R.Shear-wave splitting measurements from multishot VSP data.SEG Technical Program Expanded Abstracts，1988，7：527-530.

［4］ Winterstein D and Meadows M A.Shear-wave polarizations and subsurface stress directions at Lost Hills Field.Geophysics，1991，56（9）：1331-1348.

［5］ Zeng X and Macbeth C.Algebraic processing techniques for estimating shear-wave splitting in near-offset VSP data：theory.Geophysical Prospecting，1993，41（8）：1033-1066.

［6］ Li X and Crampin S.Linear-transform techniques for processing shear-wave anisotropy in four-component seismic data.Geophysics，1993，58（2）：240-256.

［7］ Ando M，Ishikawa Y and Yamazaki F.Shear wave polarization anisotropy in the upper mantle beneath Honshu，Japan.Journal of Geophysical Research，1983，88（B7）：5850-5864.

［8］ Bowman J R and Ando M.Shear-wave splitting in the upper-mantle wedge above the Tonga subduction zone.Geophysical Journal International，1987，88（1）：25-41.

［9］ Vinnik L P，Kind R，Kosarev G et al.Azimuthal anisotropy in the lithosphere from observations of longperiod S-waves.Geophysical Journal International，1989，99（3）：549-559.

［10］ Tian X，Zhang J，Si S et al.SKS splitting measurements with horizontal component misalignment.Geophysical Journal International，2011，185（1）：329-340.

［11］ Silver P G and Chan W W.Shear wave splitting and subcontinental mantle deformation.Journal of Geophysical Research，1991，96（B10）：16429-16454.

［12］ Gaiser J E.Advantages of 3-D PS-wave data to unravel S-wave birefringence for fracture detection.SEG Technical Program Expanded Abstracts，2000，19：1201-1204.

［13］ 张丽艳，王建民，李昂等.三维转换波叠前方位各向异性校正技术.石油地球物理勘探，2011，46（5）：695-699.Zhang Yanli，Wang Jianmin，Li Ang et al.3D converted wave prestack azimuth anisotropy correction.OGP，2011，46（5）：695-699.

［14］ Thomsen L，Tsvankin I，Mueller M C.Layer-stripping of azimuthal anisotropy from reflection shear-wave data.SEG Technical Program Expanded Abstracts，1995，14：289-292.

［15］ Dellinger J，Brandsberg-Dahl S，Clarke R et al.Alford rotation after tensor migration.SEG Technical Program Expanded Abstracts，2002，21：982-985.

［16］ 李彦鹏，马在田.快慢波分离及其在裂隙检测中的应用.石油地球物理勘探，2000，35（4）：428-432.Li Yanpeng and Ma Zaitian.Separation of fast wave from slow wave and its application to fracture detection.OGP，2000，35（4）：428-432

［17］ Simmons J.Converted-wave splitting estimation and compensation.Geophysics，2009，74（1）：D37-D48.

［18］ Yue Y，Li J，Qian Z et al.Converted-wave splitting analysis and application.75th EAGE Conference＆Exhibition Incorporating，SPE EUROPEC，2013.

［19］ Zhang J，Wang Y，Lu J.A new algorithm for frequency-dependent shear-wave splitting parameters extraction.Journal of Geophysics and Engineering，2013，10（5）：055005.

［20］ Crampin S.Geological and industrial implications of extensive-dilatancy anisotropy.Nature，1987，328（6130）：491-496.

［21］ 张中杰.地震各向异性研究进展.地球物理学进展，2002，17（2）：281-293.Zhang Zhongjie.A review of the seismic anisotropy and its applications.Progress in Geophysics，2002，17（2）：281-293.

［22］ 程冰洁，徐天吉.转换波方位各向异性裂缝检测技术研究及应用.地球物理学进展，2012，27（2）：575-581.Cheng Bingjie，Xu Tianji.Research and application of fracture detection technique using azimuthal anisotropy of C-wave.Progress in Geophysics，2012，27（2）：575-581.

［23］ 魏建新，赵群，孟平等.各向异性介质中横波特征的实验研究.石油地球物理勘探，1997，32（4）：503-511.Wei Jianxin，Zhao Qun，Meng Ping et al.Experimental researches on shear wave characteristics in anisotropic medium.OGP，1997，32（4）：503-511.

［24］ Qian Z，Zhang S，Zhao B et al.Numerical modelling of PP-and PS-wave azimuthal anisotropy in HTI media.Applied Geophysics，2012，9（4）：429-439.

［25］ 裴正林.层状各向异性介质中横波分裂和再分裂数值模拟.石油地球物理勘探，2006，41（1）：17-25.Pei Zhenglin.Numeric simulation of S-wave splitting and second splitting in layered anisotropic media.OGP，2006，41（1）：17-25.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.015

张建利，王赟，刘志斌，李绪宣.三种双扫描横波分裂算法在裂缝探测中的应用研究.石油地球物理勘探，2017，52（1）：105-113.

1000-7210（2017）01-0105-09

*北京市朝阳区太阳宫南街6号院中海油研究总院，100027。Email：jianlizhang001＠163.com

本文于2015年11月27日收到，最终修改稿于2016年11月10日收到。

本项研究受中国石油天然气集团公司科学研究与技术开发项目“弹性波地震成像技术合作研发与应用”和国家杰出青年科学基金项目（41425017）联合资助。

（本文编辑：冯杏芝）

张建利 博士，1985年生；2008年本科毕业于中国海洋大学海洋地球科学学院地球信息科学与技术专业，获理学学士学位；2014年获中科院地质与地球物理研究所固体地球物理专业博士学位；2014～2016年在中海油研究总院博士后流动站工作；现在中海油研究总院从事地震资料处理和解释。