反假频POCS数据规则化及其在偏移成像中的应用

陈小春 陈 辉 喻 勤 龙 林

（①成都理工大学，四川成都610066；②成都理工大学数字地质四川省重点实验室，四川成都610066；③中国石化西南油气分公司勘探开发研究院，四川成都610041）

反假频POCS数据规则化及其在偏移成像中的应用

陈小春*①陈 辉①②喻 勤③龙 林①

（①成都理工大学，四川成都610066；②成都理工大学数字地质四川省重点实验室，四川成都610066；③中国石化西南油气分公司勘探开发研究院，四川成都610041）

受地形条件和障碍物等因素的影响，陆上地震数据采集容易出现地震道丢失现象，对地震资料的后续处理和解释造成不良影响。文中提出一种反假频凸集投影（POCS）插值方法，借助f-k域低频成分预测高频无假频成分，剔除混叠假频，达到恢复缺失地震道的目的。Marmousi模型数据试验说明凸集投影反假频插值能提高偏移成像品质。

反假频 凸集投影（POCS） 偏移 规则化

1 引言

在野外地震数据采集过程中，受复杂环境和施工条件等影响可能导致地震数据道的缺失［1］。不规则数据会对叠加、多次波去除产生影响，产生采集脚印和画弧等问题，降低偏移成像质量。因此，在波动方程偏移等高精度处理之前，需要对不规则地震数据进行规则化处理，完成缺失数据重构［2］。

针对数据规则化问题，业界已提出了多种解决方法。Spitz［3］依据线性同相轴在f-x域的可预测性，提出f-x域预测滤波反假频插值方法，该方法能较好地处理假频问题，但仅限于规则采样的地震数据；国九英等［4］在Spitz方法的基础上对f-x域地震道插值方法做了改进，并提出f-x域等道距道内插方法，利用f-x域预测算子包含了所有反射波同相轴的倾角信息这一特性实现道内插，具有速度快、精度高、内插出的地震道波形自然、不受空间假频影响等优点，但前提是要求道内插之前道间距必须相等；为了使f-x域道内插技术更趋于合理与完善，周兴元［5］讨论了在f-x域具有固定道时间差信号的广义预测算子，并给出了道内插实现方法；Gulunay等［6］提出抗假频f-k域地震道插值方法（UFKI），用f-k域复数除法替代线性方程组求解，实现道加密插值，提高了计算效率，但只适合奇数道插值偶数道，或者偶数道插值奇数道，即两道之间只能插值出1道；国九英等［7］提出了f-k域等道距道内插方法，该方法具有抗空间假频等优点；Gulunay等［8，9］提出了广义的f-k域地震道插值方法（GFKI），可以在两道之间插值出多道；李学聪等［10］提出了f-k偏移和反偏移插值法，该方法计算速度快、没有经过近似处理、精度高，但插值道的振幅相比原始道弱；Zwartjes等［11］提出的稀疏傅里叶重建方法具有较高的插值精度，但计算成本较高；Abma等［12］将反假频凸集投影（POCS）方法从图像处理领域引入地震数据规则化，该方法易于实现且重建效果良好，但是不能抗假频，对隔道缺失的不完整地震数据插值无效，Gao等［13］通过引入倾角扫描策略解决了这一难题。

本文首先阐述了POCS数据规则化方法和反假频技术的原理及实现，在POCS算法基础上提出一种新的预测反假频数据规则化方法。该方法应用f-k域无假频低频数据建立无假频蒙板，再经过线性放大逐步预测高频数据，剔除混叠假频，达到恢复缺失地震道的目的。方法继承了POCS算法的高效性，同时具有很强的反假频能力。数值实验验证了方法的数据重建能力和在偏移成像中的作用。

2 方法原理

2.1 POCS数据规则化

受地形条件、障碍物、废道和坏道等因素的影响，实际采集地震数据多为非规则采样，而非规则采样数据通常认为是由规则数据采样不足造成的。实际采集数据可以认为是理论观测系统的数据通过稀疏采样得到的，即可以表示为

式中：dobs为含有缺失道的采集数据；S为稀疏采样算子；d为理论数据。地震数据重建问题就是由dobs恢复d。对于式（1），通过最小二乘反演可以重建缺失道，以实现观测系统数据的规则化。根据L2范数最小准则建立目标函数

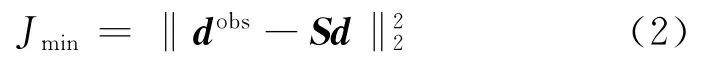
由于S为稀疏采样算子，其稀疏性会导致方程欠定、造成多解性。因此，在目标函数后增加阻尼项、建立罚函数

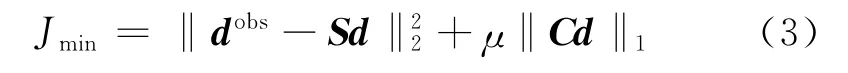
式中：C为稀疏变换算子；μ为阻尼项的权重。最小二乘法计算复杂度高、效率相对低下，对于阻尼最小二乘法来说，阻尼项在约束多解性的同时也降低了算法的收敛性能，进一步影响了最小二乘法的效率。POCS迭代方法具有更强的稳健性和收敛性，计算效率也远高于最小二乘法。在迭代步长满足收敛条件，即d i接近d的时候，式（1）可改写为

式中：i为迭代次数；d i为第i次迭代后得到的重建结果；E是单位矩阵；F及F-1分别是正、反傅氏变换算子；τi是第i次迭代时的阈值算子。

地震数据在f-k域（傅氏变换域）内的主要能量集中在其主频附近。缺失的地震道在观测系统网格中会形成空道，这些空道在f-k谱中表现为一些幅值相对较小的噪声，缺失地震道重构在f-k谱中则等效于去噪和频谱能量恢复。将含空道的原始地震数据变换到f-k域，若原始数据中的空道数量较少，则f-k谱中有效信号的能量会强于噪声能量，在这种情况下可以通过设置一个适当的阈值将低能量的频谱视为噪声截去，仅保留强能量部分。然后对所保留的频谱进行傅里叶反变换，利用频谱泄露的特性可以在空道上部分恢复出缺失信号。由于阈值的办法并不能准确区分有效信号和噪声，仅通过一次重建无法得到准确的结果。因此可降低阈值重复上述操作，经过数次迭代后f-k域中的噪声能量阈值降到远低于有效信号的水平，这时可认为数据被理想重建。

图1a和图1b是非规则数据和规则化后的数据，图1c和图1d是其对应的频谱。从图1可以看出，非规则数据在f-k域内的噪声被剔除后，t-x域的空道数据得到了很好重建，且与原始数据保持同相轴连续。

在实际数据处理过程中，阈值的选择会影响POCS数据规则化的效果。如果阈值选取过大，会导致有效信号被切除，无法正确恢复有效信号的细节。如果阈值选取过小，则大量噪声被当作有效信号予以保留，导致重建信号能量弱。为避免这两种情况，建议在迭代初期选择较大的阈值，以凸显信号同相轴的轮廓，而在后续的迭代过程中按照一定的步长衰减阈值，逐步恢复低能量部分的细节，直到阈值远低于所估计的信噪比。这样可在不伤及有效信号的前提下尽可能完整地恢复信号。本文采用线性衰减阈值，在模型中给定最大阈值τmax、最小阈值τmin以及迭代次数N，则第i次迭代时的阈值为

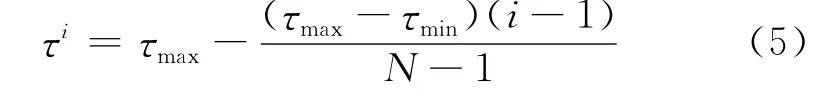
2.2 预测反假频技术

传统POCS数据规则化方法得以实现的前提是假频能量明显小于有效频谱的能量。当数据含有规则缺失道时，在f-k谱中会产生与有效频率能量相当的假频，而且假频通常与有效频谱混叠，此时就无法通过阈值的方法将假频和有效频谱分离，因此本文提出一种预测反假频技术。

首先，通过频谱分析在f-k谱中确定无假频区域的范围。将含规则缺失道的数据变换到f-k域，如图2a所示。从图中可以看到，在有效频率两侧形成严重假频，且在高频成分假频与有效频率混叠严重，但在图2a中灰色的Ⅰ区，即频率范围为［0，f1］，波数范围为［-k1，k1］，不存在假频混叠。

然后对Ⅰ区的频谱按照能量二值化，即将谱能量较大的部分置为1，很小的部分置为0，就可得到无假频蒙板。对该蒙板线性拉伸放大，扩展到Ⅱ区（图2b），则蒙板放大前、后非重叠部分即为所预测的高频有效信号的区域。

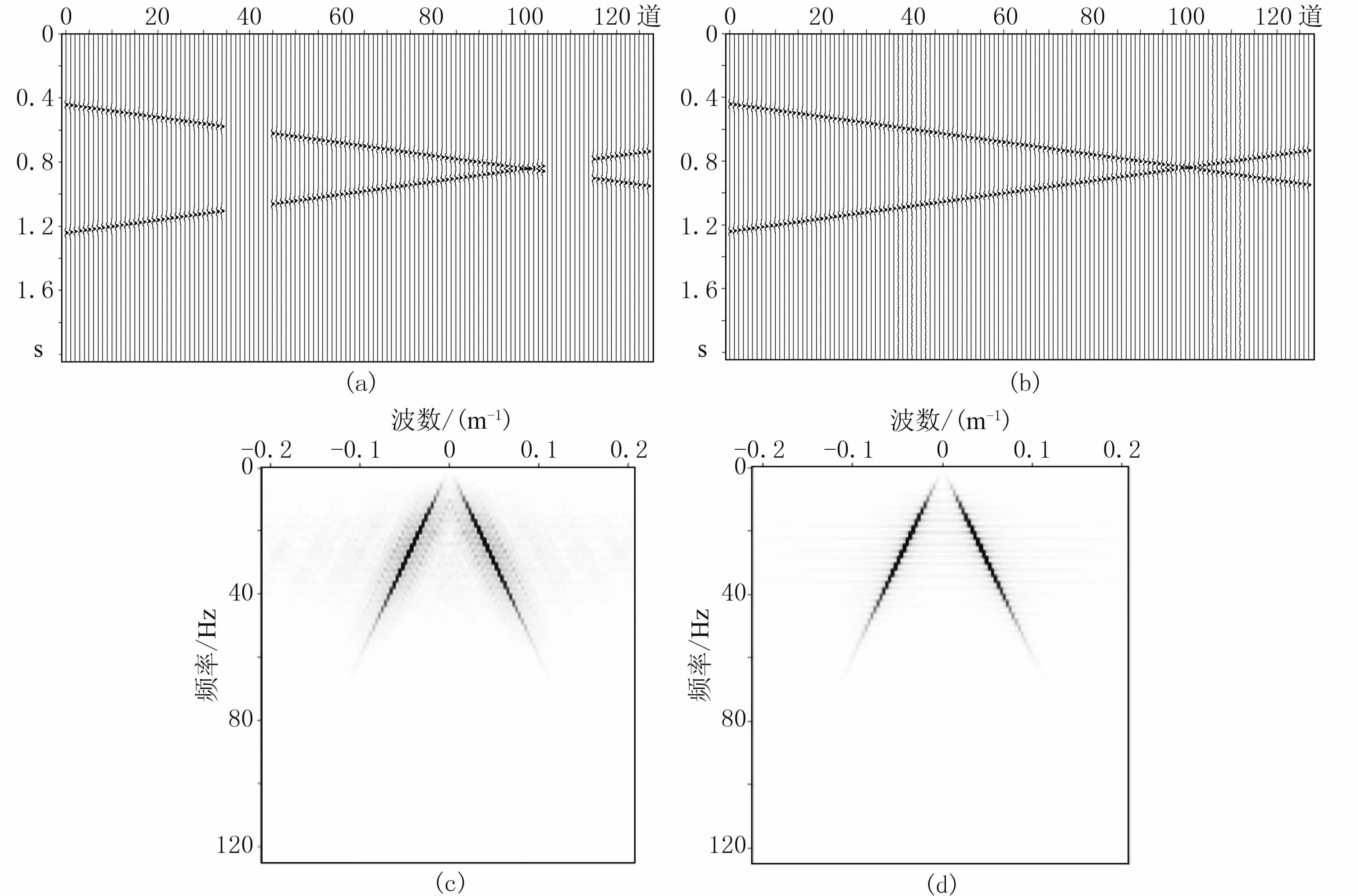
图1 POCS插值方法对含空道非规则数据的插值重建效果

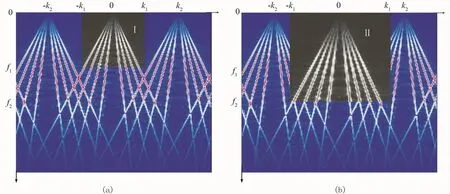
图2 预测反假频技术实现

由于蒙板本身进行了二值化，再将蒙板与频谱进行点乘，假频混叠部分乘零被剔除，只剩下有信号的有效成分。从低频向高频部分逐步预测，直到剔除所有混叠的假频。

2.3 基于POCS的预测反假频数据规则化

预测反假频技术操作简单而且能很容易地剔除混叠假频。经过拉伸放大后的反假频蒙板可以用来预测有效频率的大致范围，然而采用拉伸放大的方式决定了预测方式是线性的，实际数据的同相轴不可能做到准确的线性，这个问题可以通过开窗的办法来解决。虽然开窗可以使局部区域的同相轴线性化，但在有噪声的情况下，这种预测方式获得蒙板也会因为噪声而产生误差。这就难免会在一定程度上造成假频剔除不干净，或者伤及有效信号。但是经过反假频处理后，大部分假频能量已经被去除，误差导致的残留量已经变成随机噪声，在反假频处理之后可结合传统的POCS数据规则化方法进一步剔除噪声从而恢复有效信号。

预测反假频技术基于线性插值理论，而实际数据的同相轴不可能做到准确的线性，故反假频蒙板每次线性拉伸的步长会决定预测的精度。拉伸步长越大，预测精度越低；拉伸步长越小，预测精度越高，但是计算量也会相应的增加，必须选择合适的频率步长从低频向高频逐步处理。因此频率步长就成为权衡预测精度和计算量的重要参数。

基于POCS预测的反假频数据规则化处理步骤（图3）为：

（1）将窗口数据做二维傅氏正变换，由t-x域变换到f-k域；

（2）在f-k域中确定低频无混叠假频成分的频率范围，记为［0，f1］；

（3）对确定的无假频成分求模并做线性拉伸，拉伸到频率范围为［0，f1+df］；

（4）将拉伸后的能量谱二值化生成反假频蒙板；

（5）将反假频蒙板与原始谱相乘剔除混叠假频后做传统POCS数据规则化；

（6）判断是否已经处理到最大频率，若处理到最大频率计算结束，否则扩大无假频区域进行迭代；

（7）将规则化后的数据反变换到t-x域，将被恢复的道回填至有效信号中。

图3 预测反假频数据规则化处理流程

3 数据测试

为了检验预测反假频数据规则化方法的效果，利用简单线性模型数据进行测试。该模型是由主频为60Hz的Ricker子波合成，它包含8条斜率不同的直线同相轴，空间方向有110道，道间距为15m，时间方向共620个采样点，采样率为2ms，在该模型中数据被严重抽稀，只保留了三分之一的数据（图4a）。在实验中进行传统POCS数据规则化处理时给定的最大阈值为0.4，而最小的阈值为0.001，反假频数据规则化的迭代频率步长为6 Hz。图4c为其频谱，从中可以看出因数据道缺失而产生的幅值与主频相当的假频，且在60Hz以上出现假频混叠。图4d为重建后的频谱，经过预测反假频数据规则化处理后假频得到有效的压制，特别是在混叠部分既压制了假频，又很好地保护了有效信号。重建后的频谱反变换回t-x域，如图4b所示。空道数据被重建，从同相轴的连续性上看线性模型数据得到了正确的重建。

为验证该方法在噪声干扰下的效果，对上述数据加上信噪比为30%的随机噪声。经过同样的处理（图5）可以看出，在随机噪声和假频的同时干扰下，本文提出的方法依然可以有效地重建缺失道信号。

为了更加准确地分析重建效果，提取原始数据、不含噪声的重建数据和含有噪声的重建数据的第76道、0.40～0.50s的波形进行叠加显示（图6），可以看出三组数据的走时和振幅都基本吻合，其中原始数据和不含噪声的重建数据吻合度更高，当受到噪声影响的时候重建结果的波形和理论值存在一定的差异。

在实际数据处理过程中可能会遇到一些极端情况。比如低频部分依然存在假频混叠，就意味着数据非常稀疏，或者随机噪声过强导致无法通过阈值辨认。数据质量太差时，算法选择往往不起作用，只能通过重新采集解决。

在数据缺失非常严重的情况下，难以完全精确重建缺失的地震道，仅根据同相轴的连续性无法判断重建算法对最终处理结果的影响。本文通过Marmousi模型数据规则化前、后道集及偏移成像结果验证数据规则化对成像效果的改善能力。为了更接近实际情况，本文没有使用理论速度模型，而是用Seis＠Home软件的偏移和速度分析模块构建时间域的偏移速度模型，如图7所示。

图4 简单线性模型理论数据测试结果

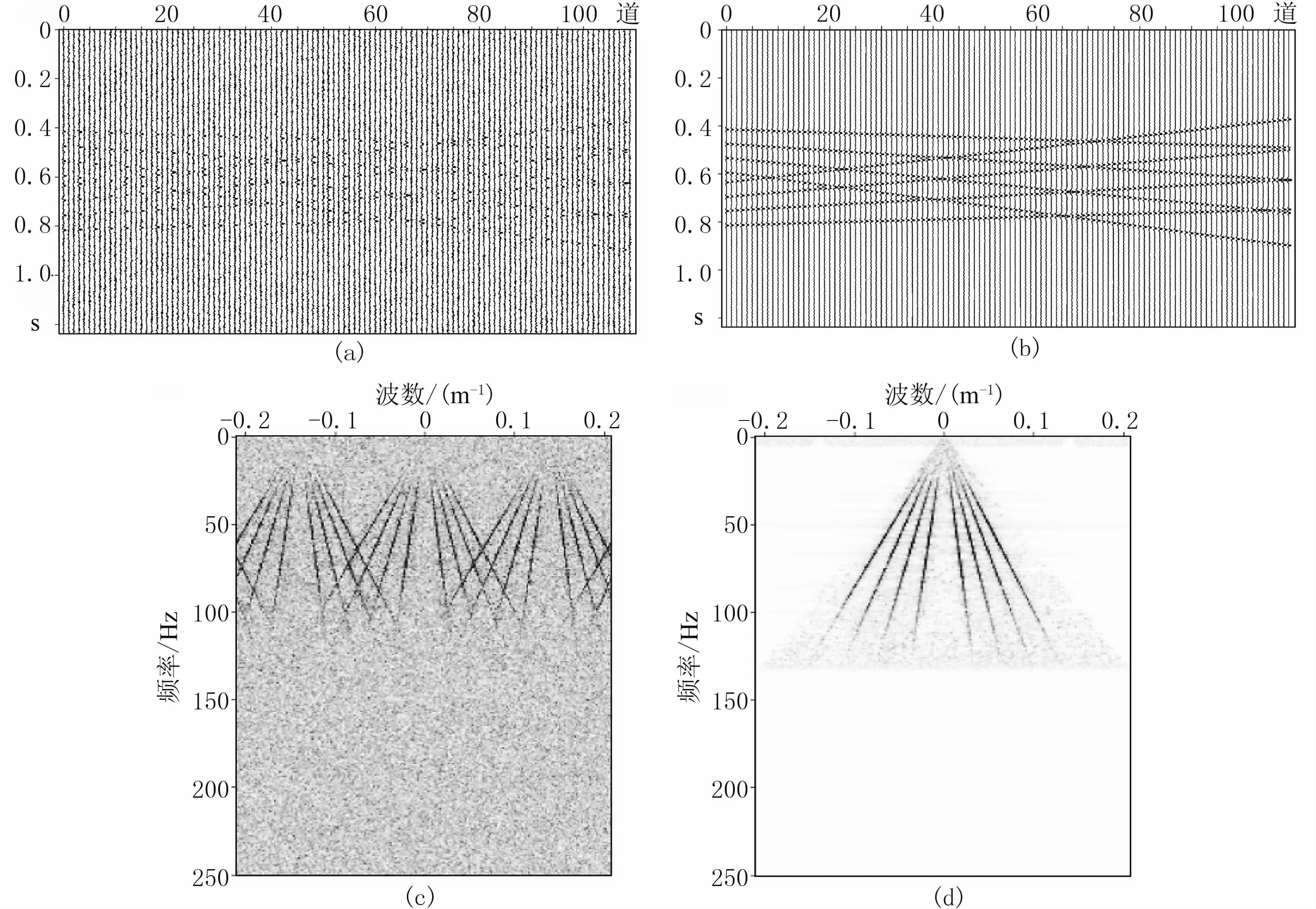
图5 简单线性模型含随机噪声数据测试结果

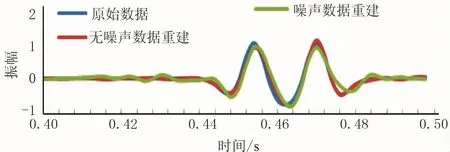
图6 三组数据第76道0.40～0.50s的波形对比

Marmousi模型数据的时域样点数为726个，时间采样率为4ms。图8a为理论的共炮检距道集数据，图8b为稀疏采样二分之一后的数据，图8c为数据规则化重建后的数据。由于Marmousi模型数据本身就比较稀疏，在大倾角构造区域肉眼可见明显的锯齿状，减少二分之一的道数据后稀疏程度更加严重，所以重建效果也不可能完全与原始数据相同。但是从Kirchhoff叠前时间偏移结果（图9）看，抽稀的数据（所有共炮检距数据都进行相同的稀疏采样）做偏移处理（图9b）后，浅层出现严重的偏移画弧现象，影响成像结果解释。然而规则化后，偏移成像（图9c）整体得到改善，特别是在中浅层效果尤为明显，偏移画弧问题得到解决。虽然在一些高陡构造区域成像能量较弱，但是有效消除了偏移噪声，突出了有效信息。

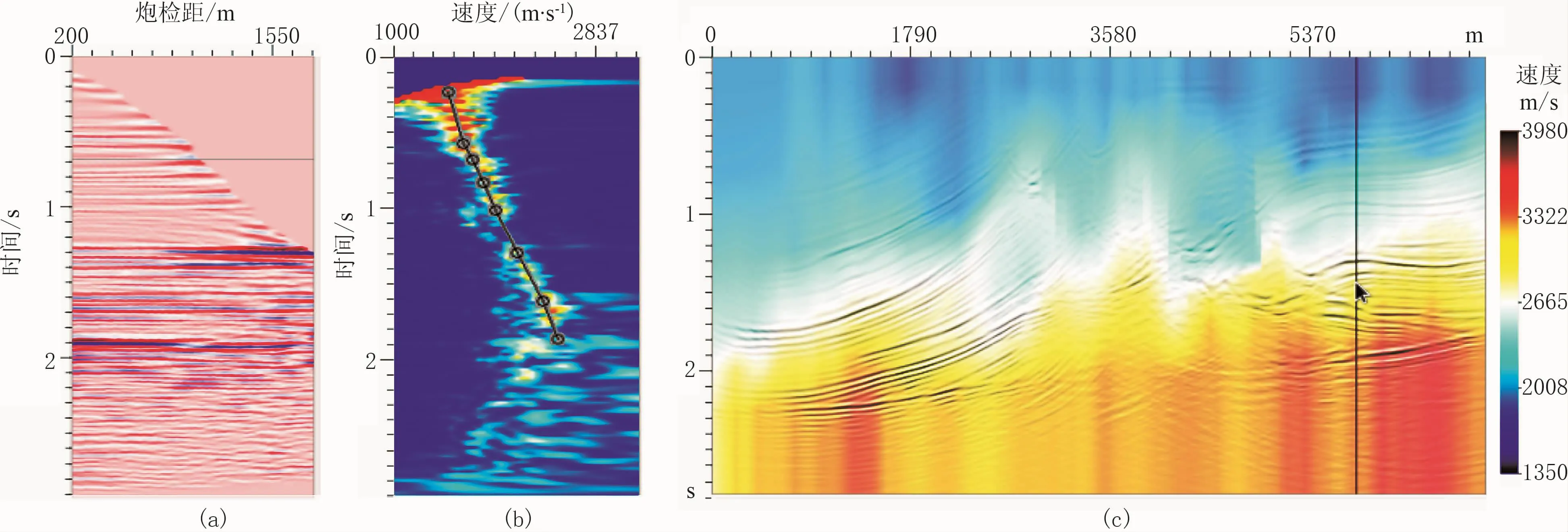
图7 时间域偏移速度建模

图8 Marmousi模型数据规则化效果

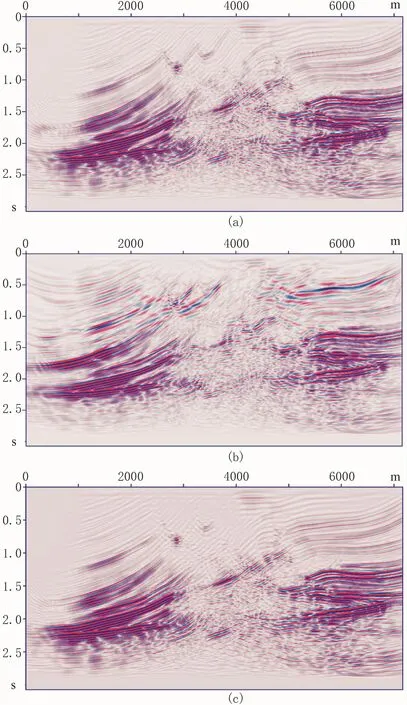
图9 数据规则化前后偏移成像结果对比

4 结论

（1）传统的POCS数据规则化方法只能重建无混叠假频的数据，而对含有混叠假频的数据不起作用。

（2）基于POCS算法的预测反假频技术能对含有混叠假频的数据进行良好的重建，而且只需较小的计算成本就能得到高质量的结果，恢复后的数据能量与其相邻道的有效数据相当，并且保持了同相轴的连续性。

（3）数据经过数据规则化处理后，偏移结果中画弧问题得到明显改善，更利于资料的解释。

［1］ 陆基孟.地震勘探原理（第三版）.山东东营：中国石油大学出版社，2011.

［2］ 黄德济，贺振华，包吉山.地震勘探资料数字处理.北京：地质出版社，1990.

［3］ Spitz S.Seismic trace interpolation in theF-Xdomain.Geophysics，1991，56（6）：785-794.

［4］ 国九英，周兴元，俞寿朋.F-X域等道距道内插.石油地球物理勘探，1996，31（1）：28-34.Guo Jiuying，Zhou Xingyuan，Yu Shoupeng.Iso-interval trace interpolation inF-Xdomain.OGP，1996，31（1）：28-34.

［5］ 周兴元.F-X域地震道内插理论及实现.石油地球物理勘探，1997，32（2）：154-162.Zhou Xingyuan.Seismic trace interpolation inF-Xdomain.OGP，1997，32（2）：154-162.

［6］ Gulunay N，Chambers E.UnaliasedF-Kdomain trace interpolation.SEG Technical Program Expanded Abstracts，1996，15：1461-1464.

［7］ 国九英，周兴元.F-K域等道距道内插.石油地球物理勘探，1996，31（2）：211-218.Guo Jiuying，Zhou Xingyuan.Iso-interval trace interpolation inF-Kdomain.OGP，1996，31（2）：211-218.

［8］ Gulunay N，Chambers E.Generalizedf-kdomain trace interpolation.SEG Technical Program Expanded Abstracts，1997，16：1100-1103.

［9］ Gulunay N.Seismic trace interpolation in the Fourier transform domain.Geophysics，2003，68（1）：355-369.

［10］ 李学聪，刘伊克，常旭等.基于F-K偏移和反偏移的地震道插值方法研究.地球物理学进展，2009，24（6）：2020-2029.Li Xuecong，Liu Yike，Chang Xu et al.Interpolation for seismic traces based onF-Kmigration and demigration.Progress in Geophysics，2009，24（6）：2020-2029.

［11］ Zwartjes P，Sacchi M.Fourier reconstruction of nonuniformly sampled，aliased seismic data.Geophysics，2004，72（1）：21-32.

［12］ Abma R，Kabir N.3D interpolation of irregular data with a POCS algorithm.SEG Technical Program Expanded Abstracts，2005，24：2150-2153.

［13］ Gao J，Stanton A，Naghizadeh M et al.Convergence improvement and noise attenuation considerations for beyond alias projection onto convex sets reconstruction.Geophysical Prospecting，2013，61（S1）：138-151.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.003

陈小春，陈辉，喻勤，龙林.反假频POCS数据规则化及其在偏移成像中的应用.石油地球物理勘探，2017，52（1）：13-19.

1000-7210（2017）01-0013-07

*四川省成都市成都理工大学地球物理学院地球物理系，610066。Email：974609310＠qq.com

本文于2015年12月4日收到，最终修改稿于2016年12月6日收到。

本项研究受国家自然科学基金项目（41304111）、四川省科技厅重点项目（2016JY0200）、四川省教育厅自然科学重点项目（14ZA0061，16ZB0101）、“油气地球物理勘探”四川省青年科技创新研究团队专项计划（2016TD0023）、成都理工大学优秀创新团队培育计划（KYTD201410）及国家科技重大专项（2016ZX05002-004-05）等联合资助。

（本文编辑：宜明理）

陈小春 1994年生；现为成都理工大学地球物理学院地球物理专业本科生，研究方向为地震信号高分辨率处理方法和重建方法及模块开发。