空间方向谱估计CLEAN算法及其在地震数据处理中的应用

孙维蔷 王华忠 符琼琲

（同济大学海洋与地球科学学院波现象与反演成像研究组，上海200092）

空间方向谱估计CLEAN算法及其在地震数据处理中的应用

孙维蔷*王华忠 符琼琲

（同济大学海洋与地球科学学院波现象与反演成像研究组，上海200092）

传统的射线束形成方法存在泄漏噪声和分辨率低的问题。为此，引入CLEAN算法，以空间方向谱作为反演解的评价准则，实现高分辨率的射线束形成。利用聚类和定位方法，进一步提高了常规CLEAN算法的空间分辨率，使该方法能更好地应用于实际地震资料去噪。理论数据和实际资料的应用结果表明，该方法可以有效压制泄漏噪声，同时提高射线束的分辨率。与传统的局部倾斜叠加和最小二乘意义下的射线束形成方法相比，文中方法具有明显的理论优势和较好的应用价值。

空间方向谱 协方差矩阵 CLEAN算法 聚类和定位 面波压制

1 引言

射线束在很多学科领域中都有重要应用，譬如雷达、射电天文、地震勘探等。应用射线束方法能够压制与有效反射波具有不同射线参数的噪声，如随机噪声及面波和多次波等线性噪声［1-3］。除了地震资料去噪，射线束的另一个重要应用是射线束偏移成像，通过射线束筛选出有效的局部方向反射波场，实现高效和高信噪比成像［4，5］。

射线束形成方法本质上是一种线性信号空间方向谱估计方法［6］。局部倾斜叠加是最常见的射线束形成方法［7］，它是线性 Radon变换（τ-P变换）的一种具体实现方式。由于τ-P变换的基函数非正交、非完备，导致其结果中包含大量的泄漏噪声，严重降低了τ-P变换的分辨率。提高射线束分辨率的基本思想是建立参数化模型预测局部线性信号，在不同类型的范数下反演估计射线束，这就将射线束形成问题转化为参数估计问题。该类方法通常用实际数据与预测数据的差作为误差范函，在最小二乘意义下估计射线束［8-10］。最小二乘意义下的估计结果在信噪比方面有比较显著的改善，但其分辨率依然受测不准原理限制。为了提高分辨率，Sacchi等［8］提出用柯西范数代替L2范数，利用有效信号的稀疏性作为约束条件，实现了频率域高分辨率的线性Radon变换；Cary［9］指出时间域的线性Radon变换结果具有更强的稀疏性，更加适合描述地震数据中的时变信号，可以更准确地估计线性信号。对于局部线性信号而言，在高斯白噪声的假设下，其对应的自相关矩阵的特征向量就是使预测误差最小的线性信号。在非高斯白噪声情况下，构造类似L1／L0范数意义下的估计可以得到更稀疏的线性信号预测结果。Hu等［10］用L1／L0范数下的稀疏求解得到了更高分辨率的射线束。总之，高分辨率的射线束形成方法可以有效地估计地震数据中的线性信号，更好地压制数据中的随机噪声，或实现更好的插值等，是一项实用价值较高的处理技术。

基于自相关矩阵分解及合成，建立误差泛函，再求解最佳逼近自相关矩阵的方向谱，是一种很有启发性的方向谱估计方法。CLEAN算法就是基于这一思想发展起来的半参数化高分辨率空间方向谱估计方法［11，12］。近年来，一类低秩近似的插值方法也是基于自相关矩阵的特征而设计的［13］。本文将CLEAN算法用于地震数据处理中，提出了一种数据驱动类射线束形成方法。在传统CLEAN算法估计空间方向谱的基础上，从协方差矩阵模型出发，结合射线束形成的正问题、协方差矩阵的正交分解和协方差矩阵拟合的反问题，并利用空间方向谱作为反演解的评价准则，估计真实的射线束。类似匹配追踪的求解方法，它能在压制泄漏噪声的同时，提高射线束估计结果的空间分辨率。引入聚类和定位算法优化了常规CLEAN算法所形成的射线束结果，可进一步提高射线束的空间分辨率。

2 理论与方法

射线束形成可以抽象地理解为：局部线性信号预测器的建立和基于该预测器的不同误差范数意义下的最优估计两个关键步骤。基于该思想，可以发展出各种不同的射线束形成方法。

2.1 L2误差范数下射线束形成方法

高精度的射线束，可以根据射线束形成的正问题，求解反问题的稀疏解得到。对于不同的频率，射线束形成正问题可以描述为

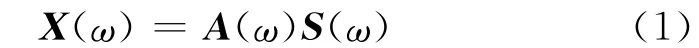
式中：ω为圆频率；向量X（ω）和S（ω）分别为单频空间局部数据向量和射线束向量；时移矩阵A（ω）中每一列向量表示射线束形成的基函数，可以表示为

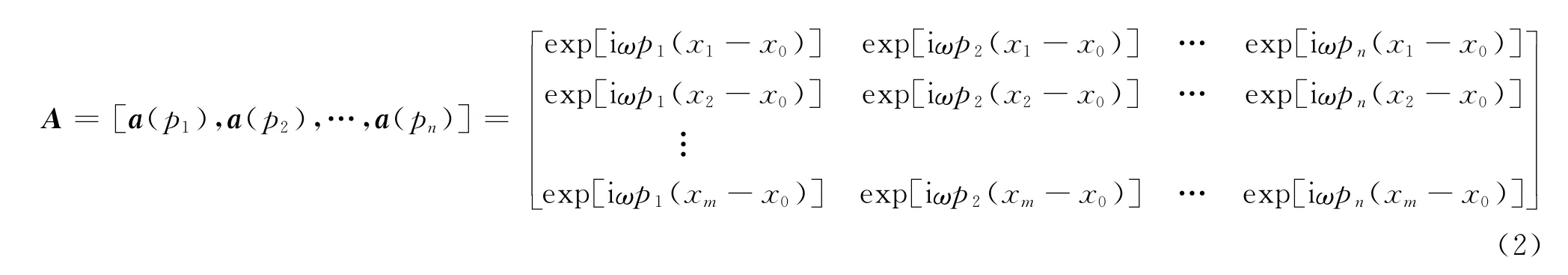
式中：m为空间局部数据的道数；n为射线参数的个数；Pi为射线参数；向量a（Pi）为射线束形成的第i个基函数；x i为局部空间数据的位置；x0为参考道的位置，通常取中心道的位置。

以上仅为二维频率—空间域正问题表达形式，更高维空间数据的排列参考螺旋坐标排列方式［14］。射线束形成方法可以从如下反演框架来解释。反问题可以描述为已知局部空间数据和时移矩阵求解射线束的过程。通过最小化目标泛函估计射线束

式中λ为权系数。该泛函的解可表示为

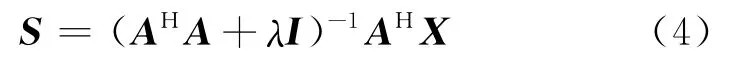
式中：“H”表示共轭转置；I表示单位矩阵。将Hessian逆矩阵项（AHA+λI）-1忽略，可得到近似解

该近似解就是局部倾斜叠加形成的射线束结果。由于时移矩阵A不是正交矩阵，所以AHA不等于单位矩阵，说明局部倾斜叠加形成的射线束结果中存在泄漏噪声和低分辨率问题。为了得到高分辨率的结果，Hessian逆矩阵项不能被忽略。但在数据孔径小的情况下最小二乘估计的射线束同样分辨率不高，需要加入先验信息约束。分辨率更高的解需要在射线束稀疏性的假设下用L1／L0范数求解。

2.2 CLEAN算法高分辨率射线束形成方法

CLEAN算法是一种半参数化的空间方向谱估计方法，它基于协方差矩阵模型拟合观测样本的协方差矩阵，实现对真实射线束的估计。求解过程类似于匹配追踪，因此它能提高射线束的空间分辨率。根据射线束形成的正问题，局部空间数据的协方差矩阵可以表示为

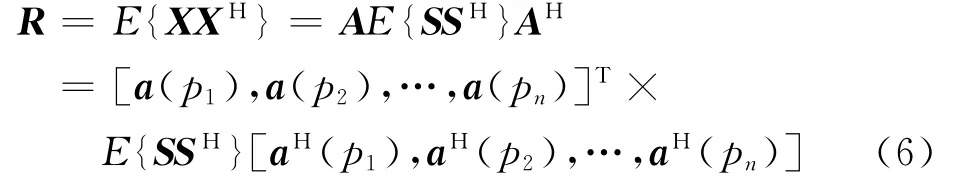
式中：R表示协方差矩阵；E｛·｝表示期望；“T”表示转置。CLEAN算法假设具有不同射线参数的射线束彼此不相关，则射线束的协方差矩阵退化为对角阵，即，其中是射线参数为P i的射线束的功率。因此，式（6）所示的协方差矩阵R可以分解为一系列与方向角度相关的子协方差矩阵

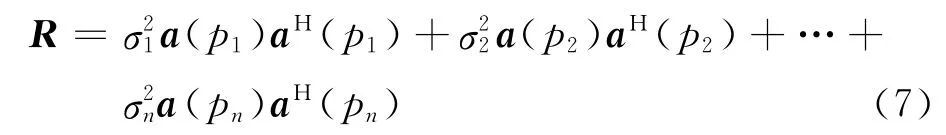
由于不能从有限的观测数据样本中精确地确定理论协方差矩阵R，因此需要由协方差矩阵的估值代替R，即式（7）为CLEAN算法所建立的协方差矩阵半参数化模型，是算法的基础，其中的每一项对应于射线参数为Pi的射线束的协方差矩阵。可以看出，所谓半参数化，主要是引入了基于局部数据估计得到的协方差矩阵。CLEAN算法根据上述协方差矩阵模型，对观测记录的协方差矩阵进行拟合的同时，估计参数，从而实现真实射线束的估计。在最小二乘意义下建立目标泛函拟合协方差矩阵

CLEAN算法通过迭代反演来逐步实现参数估计。第一步迭代假设简化式（8），建立估计参数的目标泛函

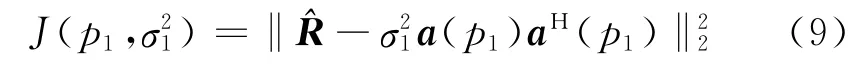
上式等价于

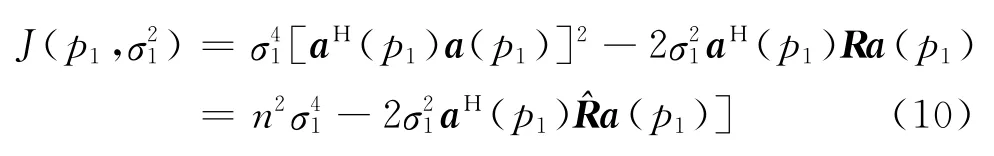
其解可以表示为

与第一次迭代类似，式（12）的解可以表示为

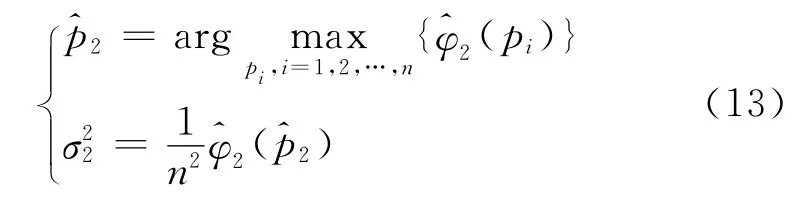
其中第二次迭代的空间方向谱为

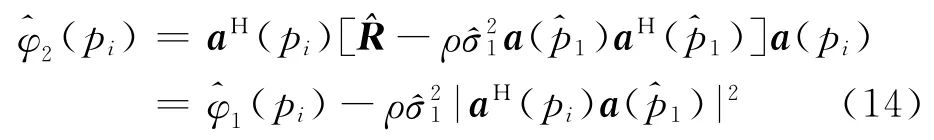
由式（13）和式（14）可知，第二次迭代是利用上次迭代所估计的参数更新协方差矩阵，由新的协方差矩阵计算空间方向谱的更新量从上一步的空间方向谱中减去该更新量的一部分，实现对空间方向谱的更新。ρ为步长，0＜ρ＜1，通常取值为0.1～0.25。ρ＜1的原因是：在空间方向谱的峰值处附近可能还存在若干个源信号，若只减去对应于参数为的空间方向谱的一部分，则在1处及其附近将剩余一些功率。在后续的迭代过程中，CLEAN算法还可以反演位于峰值1处附近的其他射线束。若将空间方向谱全部减去，可能一些射线束的谱会出现负值，这不符合物理现实。综上所述，重复以上迭代过程，直至迭代次数达到预设值或某个射线束的空间方向谱出现负值为止。

图1a数据由两个常射线参数的同相轴组成，红框圈定区域是作为输入的空间局部数据。根据采样定理，波数方向的分辨率为，其中Δx为空间采样间隔。由于波数和射线参数之间存在定量关系：k=ωP，射线束分辨率可以表示为ΔP=因此，空间局部数据窗口越小，分辨率越低。由于地震数据中的有效信号仅在局部范围内才满足线性假设，这就决定了空间局部数据的窗口不宜太大，因此局部倾斜叠加只能得到较低分辨率的射线束。图1b和图1c为局部倾斜叠加和CLEAN算法的射线束形成结果。常规局部倾斜叠加所形成的射线束中含有很强的泄漏噪声，而且分辨率较低。CLEAN算法所形成的射线束压制了大部分的泄漏噪声，同时也提高了空间分辨率。图2展示了迭代过程中的空间方向谱的变化情况。原始空间方向谱的两个峰值都集中在真实射线束成分的射线参数附近。说明空间方向谱可以作为评价真实射线束成分的有效标准。每次迭代会反演出一个真实的射线束成分，同时用来更新上次迭代的空间方向谱，直至达到终止条件。

图1 包含两个常射线参数同相轴的理论数据（a）及局部倾斜叠加（b）和CLEAN算法（c）的射线束形成结果对比

图2 迭代过程中空间方向谱的变化

为了进一步优化CLEAN算法得到的射线束的结果，提高空间分辨率，引入聚类和定位算法。在聚类算法中，根据射线束分辨率ΔP，定义了最大可分离距离εΔP，其中ε为经验参数，通常ε=0.5。聚类算法的作用是对常规CLEAN算法所确定的射线束进行分类，所有距离小于最大可分离距离的射线束归为同一个射线束。当空间局部窗内波现象较复杂时，常规CLEAN算法所确定的射线束存在假象，进而降低了空间分辨率。据此，聚类算法可以用于优化常规CLEAN算法，进一步提高射线束的空间分辨率。

定位算法的作用是确定每一类射线束中的真实射线束的位置。利用加权均方差建立泛函来估计每一类射线束中真实射线束成分的位置，即

式中：l ij表示第i类中的第j个射线束的位置，hij是其振幅值；¯h i是第i类中所有射线束的平均振幅值；Ni为第i类射线束的射线个数。求解泛函式（15），得到第i类射线束中的真实射线束位置的估计值

3 数值试验

3.1 理论数据测试

图3a为有限差分正演所得的单炮记录，其中红框区域为用于形成射线束的空间局部数据。图3b～图3d比较了局部倾斜叠加、最小二乘反演和高分辨率CLEAN算法所形成的射线束。由于局部倾斜叠加的基函数非完备正交，导致结果中包含大量的泄漏噪声，这些噪声会严重降低射线束的空间分辨率；最小二乘意义下的射线束估计结果在信噪比方面有比较显著的改善，但其分辨率依然受测不准原理限制，空间积分孔径越小，分辨率越低；高分辨率的CLEAN反演方法不仅压制了泄漏噪声，同时也提高了空间分辨率。图4描述了迭代过程中空间方向谱的变化情况。原始空间方向谱的峰值都集中在对应于真实射线束成分的射线参数附近，说明空间方向谱可以作为评价真实射线束的有效标准。每次迭代会反演出一个真实的射线束，同时更新了上次迭代的空间方向谱，直至达到迭代终止条件为止。空间方向谱在迭代过程中的变化证明了新方法可以通过逐步迭代，有效地反演出真实射线束。

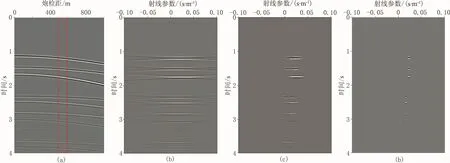
图3 理论记录不同方法的结果对比

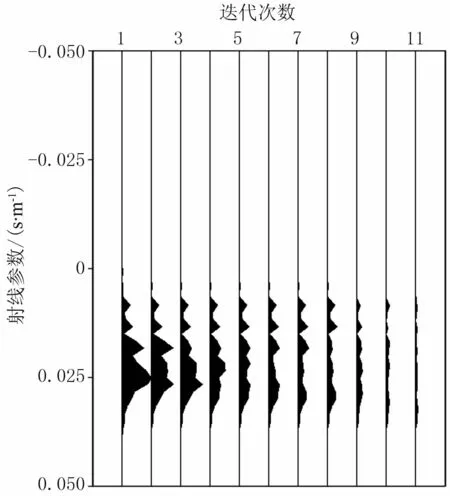
图4 迭代过程中空间方向谱的变化

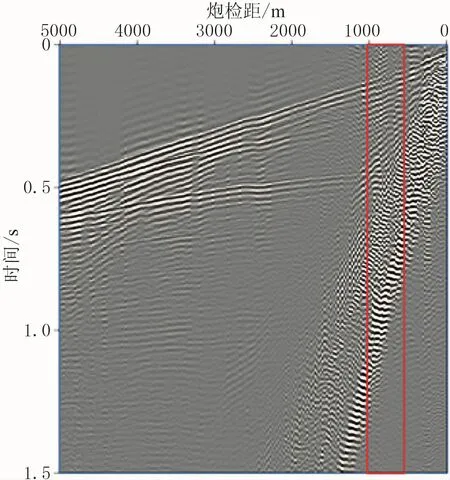
图5 实际单炮记录

3.2 实际数据测试

将基于CLEAN算法的高分辨率射线束形成方法用于实际数据压制面波噪声。面波压制过程中，首先利用基于CLEAN算法的高分辨率射线束形成方法将时空域中的观测记录变换到局部平面波域；在平面波域中根据有效信号与面波的可分离性，对面波进行压制；最后将平面波域压制面波后的记录反变换回时空域。图5为野外观测的单炮记录，其中面波能量很强。图6对比了图5红框区域中数据的局部倾斜叠加和基于CLEAN算法所形成的射线束。由于基函数非完备正交且观测孔径有限，局部倾斜叠加形成的射线束中存在大量泄漏噪声且空间分辨率低，模糊了面波在平面波域的特征，难以实现面波与有效波的分离（图6a）。在CLEAN算法产生的射线束中，由于泄漏的噪声得到了压制且空间分辨率较高，使得面波和有效波可以明显区分（图6b，红色箭头所指即为面波区域）。在基于CLEAN算法的高分辨率射线束形成方法的基础上，可以通过切除压制面波。图7为压制面波后的炮记录及压制掉的面波，可以发现，大部分面波已经被压制，证明了本文方法的有效性。

4 结论与讨论

基于CLEAN算法的高分辨率射线束形成方法从协方差矩阵的半参数化模型出发，以射线束形成的方向谱的分辨率作为反演解的评价标准，实现真实射线束的估计，提高了射线束的空间分辨率。数值试验结果证明了本方法在提高射线束空间分辨率方面的有效性和可行性，未考虑提高射线束时间分辨率是本文方法的不足之处。将高分辨率射线束形成方法用于实际资料的面波压制中，取得了较好的效果。除了面波压制，高分辨率的射线束形成方法还可以应用于线性与随机噪声压制、地震数据规则化、地震数据压缩和射线束偏移等地震数据处理中，具有重要的应用价值。

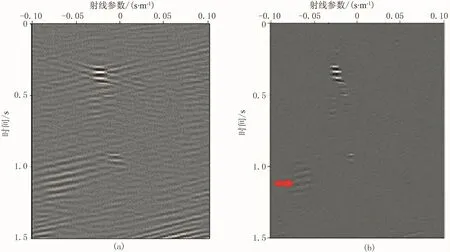
图6 实际数据不同方法形成射线束对比

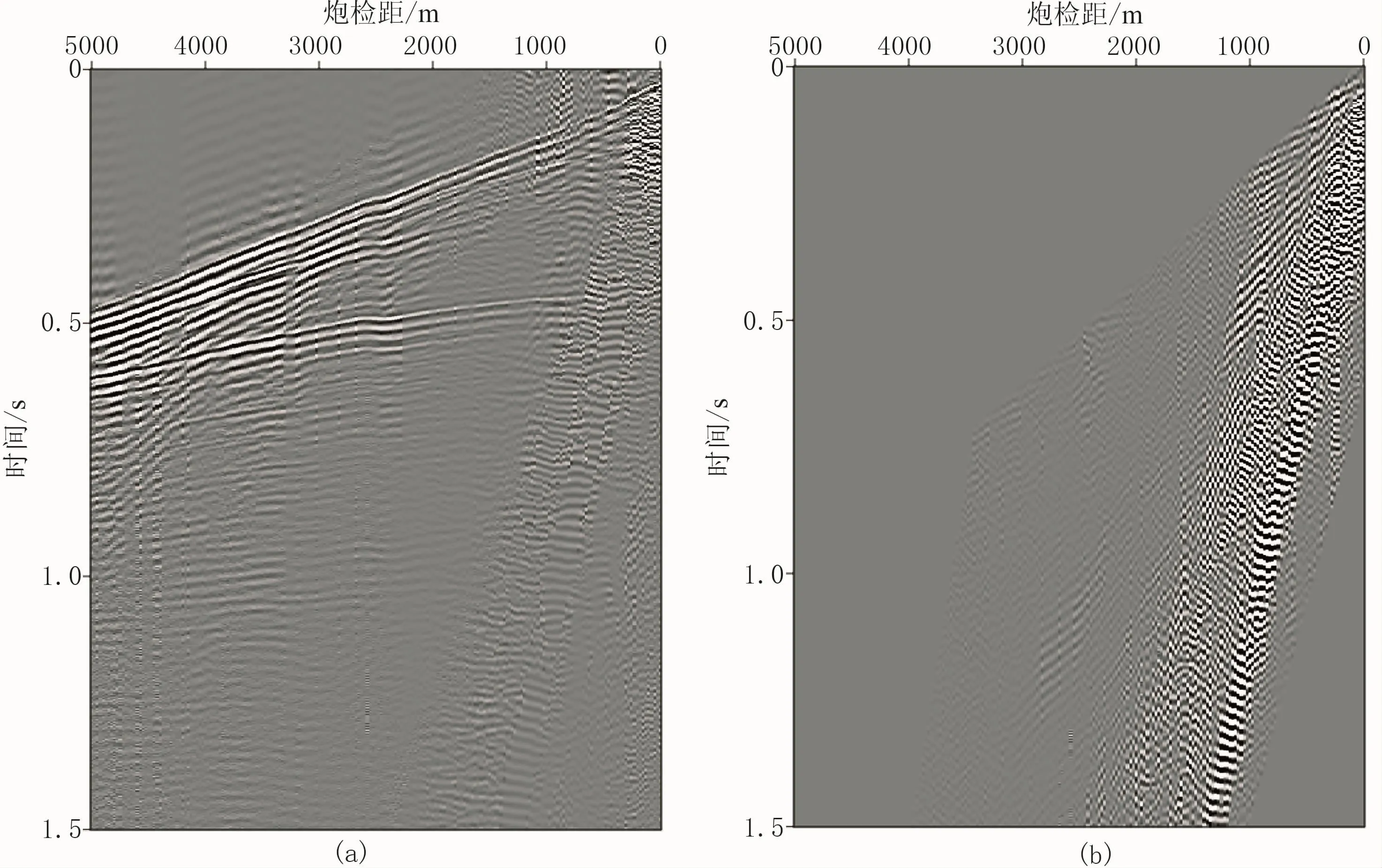
图7 实际数据面波压制后的单炮记录（a）及压制的面波（b）

［1］ 张军华，吕宁，田连玉等.地震资料去噪方法综合评述.石油地球物理勘探，2005，40（S1）：121-127.Zhang Junhua，LüNing，Tian Lianyu et al.Overview of seismic data de-noising methods.OGP，2005，40（S1）：121-127.

［2］ 朱生旺，魏修成，李锋等.用抛物线Radon变换稀疏解分离和压制多次波.石油地球物理勘探，2002，37（2）：110-116.Zhu Shengwang，Wei Xiucheng，Li Feng et al.Separating and suppressing multipies by sparse solution of parabolic Radon transform.OGP，2002，37（2）：110-116.

［3］ 吴艳辉，唐博文，柯本喜等.GeoEast多次波压制技术在陆上地震资料处理中的应用.石油地球物理勘探，2014，49（S1）：93-98.Wu Yanhui，Tang Bowen，Ke Benxi et al.Multiple suppression technique based on GeoEast and its application on onshore seismic data processing.OGP，2014，49（S1）：93-98.

［4］ Gray S H.Gaussian beam migration of common-shot records.Geophysics，2005，70（4）：S71-S77.

［5］ 王华忠，冯波，刘少勇等.叠前地震数据特征波场分解、偏移成像与层析反演.地球物理学报，2015，58（6）：2024-2034.Wang Huazhong，Feng Bo，Liu Shaoyong et al.Characteristic wavefield decomposition，imaging and inversion with prestack seismic data.Chinese Journal of Geophysics，2015，58（6）：2024-2034.

［6］ Stoica P，Mosese R L.Spectral Analysis of Signals.Prentice-Hall，Upper Saddle River，New Jersey，2005.

［7］ Neidell N S，Taner M T.Semblance and other coherency measures for multichannel data.Geophysics，1971，36（3）：483-497.

［8］ Sacchi M，Ulrych T.High-resolution velocity gathers and offset space reconstruction.Geophysics，1995，60（4）：1169-1177.

［9］ Cary P.The simplest discrete Radon transform.SEG Technical Program Expanded Abstracts，1998，17：1999-2002.

［10］ Hu J，Wang X，Wang H.Beam forming by least square inversion with radon spectrum constraints.SEG Technical Program Expanded Abstracts，2012，31：PAPR1140.

［11］ Högbom J A.Aperture synthesis with a non-regular distribution of interferometer baselines.Astronomy＆Astrophysics Supplement，1974，15（15）：417-426.

［12］ Cornwell T and Bridle A.Deconvolution Tutorial（Technical report）.National Radio Astronomy Observatory，1996.

［13］ Yang Y，Ma J，Osher S.Seismic data reconstruction via matrix completion.Inverse Problems and Imaging，2013，4（4）：1379-1392.

［14］ Rickett J E and Claerbout J F.Calculation of the Sun＇s acoustic impulse response by multi-dimensional spectral factorization.Solar Physics，2000，192（1）：203-210.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.004

孙维蔷，王华忠，符琼琲.空间方向谱估计CLEAN算法及其在地震数据处理中的应用.石油地球物理勘探，2017，52（1）：20-26.

1000-7210（2017）01-0020-07

*上海市同济大学海洋与地球科学学院波现象与反演成像研究组，200092。Email：tswq_123456＠msn.com

本文于2016年1月28日收到，最终修改稿于同年12月3日收到。

本项研究受国家重点基础研究“973”发展计划项目（2011CB201002）和国家科技重大专项（2011ZX05005-005-008HZ）联合资助。

（本文编辑：宜明理）

孙维蔷 博士，1988年生；2010年获同济大学海洋与地球科学学院地球物理学专业学士学位；2016年获该校海洋与地球科学学院地球物理学专业博士学位，主要从事多次波压制与成像方法研究。