基于稀疏表示的非零井源距VSP波场分离方法

赵彦青 萧蕴诗

（同济大学电子与信息工程学院，上海201804）

基于稀疏表示的非零井源距VSP波场分离方法

赵彦青*萧蕴诗

（同济大学电子与信息工程学院，上海201804）

随着垂直地震剖面（VSP）技术的不断发展，高保真的波场分离成为VSP资料处理与应用的关键之一。引入欠定盲源分离思想，利用VSP波场的极化特征及多分量资料在时频域的稀疏性，提出一种基于稀疏表示的波场分离方法。该方法分为两步：第一步将地震信号变换到时频域，并估计极化矩阵；第二步在时频域分离各单一波场，再反变换回时间域。在第二步波场分离过程中，针对时频域波场稀疏性不足的情况，提出一种改进的最短路径分解法，在一定程度上解决了时频域局部信号混叠的问题。模型试算与实际资料处理结果表明，与传统方法相比该方法能够更准确地分离上、下行P-P波、P-SV波，分离后的波场保幅性较好，不存在混波、假频以及边界问题。

非零井源距VSP 多分量 波场分离 欠定盲源分离 稀疏表示

1 引言

垂直地震剖面（VSP）是一种地面激发、井中观测的地震勘探技术。与地面地震资料相比，VSP资料信噪比和分辨率高，具有更明显的地震波运动学与动力学特征。由于观测方式的特殊性，VSP资料波场非常丰富，不同的波场能够解释不同的地球物理现象，因而高保真的波场分离是VSP资料处理的关键之一。

传统的VSP波场分离方法有很多，按照数据类型可分为两类：一类是针对单分量数据的波场分离，其中有的方法根据不同波场视速度差异进行数学变换，在变换域内完成波场分离再反变换，如f-k滤波、Radon变换等［1］，还有的方法对某一类型波场进行衰减或增强，达到波场分离的目的，如中值滤波、均值滤波等；另一类是基于多分量数据的波场分离，如根据不同波场极化特征的极化滤波方法、变速视慢度法等［2-5］。这些方法都有各自的优势，但也存在一定的缺陷。常规f-k滤波、Radon变换法都会引起波场的畸变；中值滤波在分离上行P-P波、P-SV波时会造成有效波场损伤，并且存在边界问题；常规极化滤波虽然具有较好的保幅性，但采用直达波传播方向确定极化角仅在直达P波与上行P-P波极化方向完全正交时分离效果较好。针对传统方法的不足，Wang等［6］提出了利用检波点位置的速度与密度等参数在τ-P域实现多分量地震数据P波与SV波的分离；Blias［7］提出一种 wave-by-wave波场分离方法，根据振幅与视速度的不同实现逐波分离；王成礼［8］根据不同观测方式下VSP的波场特征提出了不同的波场分离方法；杜婧等［9］通过估计局部斜率参数分离VSP波场，克服了传统方法的滤波阈值镶边问题；崔汝国等［10］提出了浮动坐标系极化滤波，建立极化方向随深度变化的滤波坐标系，提高了极化滤波的精度；孙文博等［11］提出一种基于参数反演的矢量波场分离方法，在分离波场的同时反演出速度、极化角等参数；马志霞等［12］进一步对多种VSP波场分离方法进行了对比，取得了良好的应用效果；Jiang等［13］利用高精度抛物线Radon变换分离P-P波与P-SV波波场，提高了波场分离的精度。

盲源分离（BSS）理论是现代信号处理领域的一个崭新的研究方向。这里的“盲”有两层含义：一是源信号不能被观测；二是传输信道不可知或者难以估计。盲源分离算法对系统的先验知识要求甚少，具有广阔的应用前景，近年被引入地震资料波场分离领域［14］。Van der Baan［15］提出了在τ-P域利用独立分量分析（ICA）分离PP波与PS波，仅利用二者统计上的区别，而无须知道速度、密度等参数；Vrabie等［16］提出高阶奇异值分解（HOSVD）和单峰独立分量分析子空间算法，在波场分离过程中具有较好的抗噪性；Liu等［17］提出了基于信息最大化原则的地震信号盲源分离方法，利用高阶统计量分离多次波。

将不同类型的VSP波场看作彼此独立的源信号，多分量VSP波场分离问题属于典型的欠定盲源分离（UBSS）问题，即观测信号（VSP分量）个数小于源信号（VSP波场）个数。目前，基于稀疏表示（SR）的方法已经成为欠定盲源分离主要方法。本文利用VSP波场的极化特征，提出一种基于稀疏表示的VSP波场分离方法，该方法能够同时分离出上、下行P-P波、P-SV波，既保留了极化滤波保幅性较好的优势，又不存在二维滤波产生的波场畸变问题。

2 欠定盲源分离问题

假设有N个未知的源信号s1（t），s2（t），…，s N（t），经过一个未知的混合系统后，得到M个观测信号x1（t），x2（t），…，x M（t），不考虑噪声的影响，则瞬时线性混合模型的数学描述为

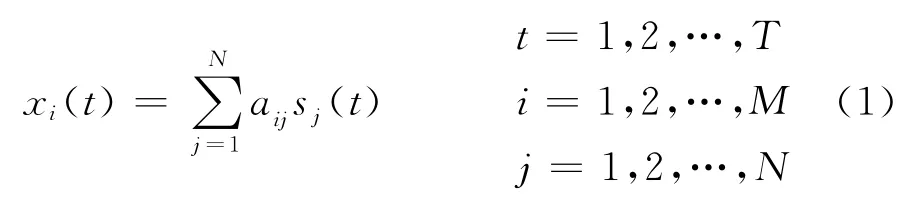
式中aij为混合系数。式（1）可以写成矩阵形式

其中：X是M×T维的观测信号矩阵；S为N×T维的源信号矩阵；A表示M×N维混合矩阵。盲源分离的主要任务就是在仅通过观测信号X来获取源信号S的估计。对于M=N的情况，经典的盲源分离方法通过寻找一个分离矩阵W来完成源信号的估计，即

对于非零井源距VSP（Offset VSP），定义三分量检波器三个分量接收的记录为r x、r y、rz，在各向同性介质中，SH波经过检波器定位后完全被旋转到y分量（即与炮检平面垂直的方向），P-P波与P-SV波则旋转到x-z平面（即炮点检波点所在的平面）。因为SH波较容易分离，本文主要考虑P-P波与P-SV波的分离。为了书写方便，仍用r x表示检波器定位后的x分量。

图1 检波器定位后的VSP波场（x-z平面）

检波器定位后的x-z平面如图1所示。在某一时刻t，定义检波器接收的上行P-P波为uP，上行P-SV波为uSV，下行P-P波为dP，下行P-SV波为dSV，水平分量为r x，垂直分量为rz，θuP、θuSV、θdP、θuSV分别为上行P-P波、上行P-SV波、下行P-P波、下行P-SV波传播方向与x轴的夹角，即各个单一波场的极化角，存在如下关系

上式可以简写为

式中：r为t时刻x、z两分量记录；p为极化矩阵，其元素即为各个单一波场的传播方向分别在x、z轴上的单位矢量投影；s为t时刻各上、下行P-P波、P-SV波单一波场。可以看出，在p未知、s也未知的情况下，仅凭r来估计s是典型的欠定盲源分离问题，极化矩阵p即为盲源分离问题中的混合矩阵，s为源信号。

3 基于稀疏表示的VSP波场盲分离

稀疏表示的数学模型与盲源分离模型一致，也可以用式（5）表示，稀疏表示的目标就是估计恰当的p与s，使s尽可能稀疏。稀疏性有两层含义：其一是指源信号本身服从稀疏分布，大多数时刻取值为零或接近于零；其二是在某一时刻，只有很少的源信号取值较大。如果信号本身的稀疏性并不理想，则需要进行某种线性变换T，使信号在变换域内更具有稀疏性。由于T是线性变换，极化矩阵在变换前后保持不变，由式（5）可得

由于VSP波场复杂，单一波场在时间域的稀疏性较差，因而首先采用短时傅里叶变换（STFT）或小波变换将地震信号从时间域变换到时频域，在时频域进行波场分离后，再将分离的波场变换回时间域。

3.1 极化矩阵的估计

传统的极化滤波方法认为直达P波的极化方向与上行P-SV波极化方向相同，而上行P-P波与下行P-SV波的极化方向相同，因而利用直达P波计算极化角，通过极化滤波分离上行P-P波与上行P-SV波。这种做法有很大缺陷：一是时直达P波与上行P-SV波极化方向不同；二是随着地层深度的增加，各个波场的极化角是变化的，利用单一的直达P波极化角对整道数据进行极化滤波显然不合理，因此必须对极化角进行时变估计。

首先将地震记录r变换到时频域，r的STFT可以表示为

式中：h为窗函数；t为时间；ω为角频率。由于STFT是线性变换，式（6）可以写为

在时频域对估计极化角做如下假设。

（1）在以某一时刻tj为中心的时频窗（tj，ωk）内仅有单一波场Si发育，即

式中：Si是时间域源信号s i的STFT；j为时间采样点；k为频率采样点。显然存在

式中：Rz（tj，ωk）、Rx（tj，ωk）分别为z分量和x分量的STFT变换；αi为各单一波场的极化角。

（2）在以t j为中心开始的连续K个时频窗内，各单一波场的极化角保持不变，即

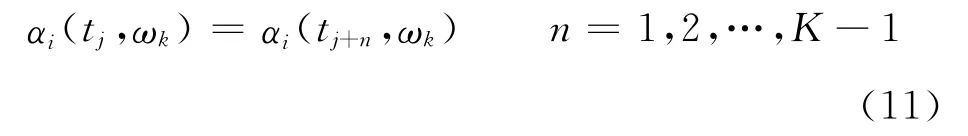
计算K个时窗内的极化角均值与方差，即

如果在K个时频窗内存在var（αi）=0，则说明此时仅存在单一波场Si，且其极化角为（t j，ωk）。逐一计算扫描整个时频域数据，得到所有的单源时频点及相应的极化角簇（l=1，2，…，L）。采用K-means聚类算法，将按照波场类型聚成4类φ=｛φ1，φ2，φ3，φ4｝，假设每类中的元素数为H=｛H1，H2，H3，H4｝，类心为，同一类之间的紧密程度定义为

3.2 单一波场的估计

对于欠定盲源分离，即使已知混合矩阵，源信号依然是多解的。稀疏表示的最终目标是得到最稀疏的s，也就是说使s中尽可能多的元素取值为零，数学上可以归结为L0范数优化问题

式中：为s的估计；为L0范数稀疏测度。虽然L0范数最能体现稀疏性的含义，但是求解对噪声太敏感、鲁棒性差，因而难以有效实现，所以Donoho等［19］建议采用L1范数稀疏测度代替L0范数，即

单一波场的估计仍在时频域进行，按照稀疏性理想程度分以下几种情形进行分析。

（1）如果在时频域单一波场源信号足够稀疏，即在每一个以t j为中心的时频窗（t j，ωk）内仅有唯一的单一波场Si发育，则最小L1范数解能够非常好地逼近单一波场源信号，有

式中αi（t j，ωk）为当前时频窗内单一波场Si的极化角。

（2）如果在每一个以tj为中心的时频窗（tj，ωk）内仅有两种波场发育，此时可以用最短路径分解法对波场进行估算。图2a为最短路径分解法示意图，在Rx-R z平面中，O为原点，R为观测信号在时频域中的某一点，其矢量方向与R x轴的夹角为θ，即当前时刻的极化角可由式（10）计算。a1和a2为离θ最近的两种波场的基矢量，也是极化矩阵的列向量。沿着a1和a2的方向做平行四边形，分解向量R，则有

（3）如果在每一个以t j为中心的时频窗（tj，ωk）内不少于三种波场发育，由于多源干涉，最短路径分解法对源信号的估计效果会较差。下面以三种单一波场源信号为例，提出一种改进的最短路径分解法。

如图2b所示，a1和a2仍为离θ最近的两种波场的基矢量，a3为离θ较远的波场基矢量，有

图2 最短路径分解法及其改进方法示意图

首先通过以上方法估计离tj最近时刻t′j的单源频率点。由VSP真振幅恢复的补偿公式可推导出与的关系

式中n为补偿因子，可利用tj与t′j段的时间—能量对进行最小平方拟合获得。

根据以上假设条件，基矢量a3在一定时间段内保持不变，即

将向量R与a3方向的向量作矢量相减，有

然后再利用最短路径法分解R′，估计出与，就完成了全部单一波场的估计。

综上所述，基于稀疏表示的VSP波场盲分离包括以下几个步骤：

（1）对原始的VSP水平分量做检波器定位，得到定位后的x分量；

（2）对定位后的x分量与原始z分量做STFT，将信号变换到时频域；

（3）将时频窗按时间分段，估算各时间段内单一波场的极化角；

（4）在时频域内应用改进的最短路径分解法，估算各时间段内的单一波场；

（5）对时频域的单一波场做STFT反变换，得到时域的单一波场。

4 数值计算

4.1 模型试算

采用如图3a所示的三层水平模型，检波器起始深度为500m，共100级，级间距为20m，井源距为1000m。图3b、图3c分别为正演模拟的非零井源距VSP水平分量记录与垂直分量记录，可以看出，记录中包含上、下行P-P波与上、下行P-SV波多种类型的波场。由于极化方向不同，各个波场在水平分量与垂直分量记录上的强弱关系也不同。

图3 模型示意图及正演模拟记录

图4为模型数据波场分离结果，可以看出，f-k滤波分离的上行P-P波中仍含有下行波的痕迹（图4a中椭圆内），这是由于二维傅里叶变换会产生空间假频问题。中值滤波分离的上行P-P波中仍存在下行波、上行P-SV波的痕迹（图4b中椭圆内）。一方面中值滤波对排齐要求较高，而对于非零井源距VSP，不同深度界面反射的波场无法同时排齐，造成滤波后仍存在残余波场能量；另一方面中值滤波存在边界效应，在边界处无法完全分离单一波场。由于在时频域单一波场的稀疏性较好，通过本文方法分离的上行P-P波质量较高，既没有二维滤波带来的波场畸变，又考虑了波场的偏振特征，因而具有较好的保幅性。

4.2 实际资料处理

图5是实际非零井源距VSP资料。由于原始地震记录上存在噪声，而本文讨论的数学模型是无噪的，因而先对记录进行随机噪声衰减，再进行波场分离。图6为实际资料波场分离结果。可以看出：f-k滤波分离的波场存在混波现象（图6a中椭圆内）；中值滤波分离的波场信噪比较低，存在明显的下行波残余能量（图6b中椭圆内），且同相轴连续性较差；本文方法分离的波场同相轴清晰，波场连续，分离效果优于f-k滤波与中值滤波。

5 结论

本文介绍了盲源信号分离的基本原理，在此基础上提出了一种基于稀疏表示的VSP波场分离方法。该方法首先将VSP地震信号变换到时频域，然后基于稀疏性假设对各个单一波场的极化角进行估计，进而估算极化矩阵，再根据各个单一波场在时频域的极化特征，采用改进的最短路径法对单一波场进行分离。由于极化矩阵在线性变换下保持不变，该方法能够得到保真性较好的上、下行P-P波、PSV波，处理效果优于传统的f-k滤波与中值滤波。模型试算与实际资料处理效果验证了本文方法的有效性。

图4 模型数据波场分离结果

图5 检波器定位后的实际非零井源距VSP资料

［1］ Moon W，Carswell A，Tang R et al.Radon transform wave field separation for vertical seismic profiling data.Geophysics，1986，51（4）：940-947.

［2］ Esmersoy C.Inverse of P and SV waves from multicomponent offset vertical seismic profiles.Geophysics，1990，55（1）：39-50.

［3］ Cho W H and Spencer T W.Estimation of polarization and slowness in mixed wavefields.Geophysics，1992，57（6）：805-814.

［4］ 魏修成，吴律，田子奇.变速视慢度波场分离.石油地球物理勘探，1993，28（4）：418-429.Wei Xiucheng，Wu Lüand Tian Ziqi.Wavefield separation using apparent slowness of variable velocity.OGP，1993，28（4）：418-429.

［5］ Anderson S，Nehorai A.Analysis of polarized seismic wave model.IEEE Transactions on Signal Processing，1996，44（2）：379-386.

［6］ Wang Y B，Singh SC and Barton P J.Separation of P-and SV-wavefields from multi-component seismic data in theτ-Pdomain.Geophysical Journal International，2002，151（2）：663-672.

［7］ Blias E.VSP wavefield separation：Wave-by-wave optimization approach.Geophysics，2007，72（4）：47-55.

［8］ 王成礼.VSP不同观测方式的波场特征与波场分离方法.石油地球物理勘探，1990，25（2）：148-160.Wang Chengli.Various VSP wave fields generated by different observation ways and the corresponding wave field separation methods.OGP，1990，25（2）：148-160.

［9］ 杜婧，王尚旭，刘国昌等.基于局部斜率属性的VSP波场分离研究.地球物理学报，2009，52（7）：1867-1872.Du Jing，Wang Shangxu，Liu Guochang et al.VSP-wavefield separation using local slopes attribute.Chinese Journal of Geophysics，2009，52（7）：1867-1872.

［10］ 崔汝国，牟风明，宋维琪等.VSP浮动坐标系偏振滤波.石油地球物理勘探，2010，45（1）：10-14.Cui Ruguo，Mu Fengming，Song Weiqi et al.Polarization filtering with drift coordinates for VSP data.OGP，2010，45（1）：10-14.

［11］ 孙文博，孙赞东.3D3C VSP资料处理中矢量波场分离方法的研究.石油地球物理勘探，2009，44（6）：708-719.Sun Wenbo，Sun Zandong.Studies on vector wave field separation method for 3D3C VSP data.OGP，2009，44（6）：708-719.

［12］ 马志霞，孙赞东，白海军等.三维三分量VSP多种波场分离方法对比.石油地球物理勘探，2010，45（2）：219-224.Ma Zhixia，Sun Zandong，Bai Haijun et al.Comparative studies on 3D3C VSP multiple wave field separation methods.OGP，2010，45（2）：219-224.

［13］ Jiang X，Lin J，Ye F et al.Separation of P-P and P-SV wavefields by high resolution parabolic Radon transform.Journal of Applied Geophysics，2015，119（8）：192-201.

［14］ Moni A，Bean C J，Lokmer I et al.Source separation on seismic data：Application in a geophysical setting.IEEE on Signal Processing，2012，29（3）：16-28.

［15］ Van der Baan M.PP／PS wavefield separation by independent component analysis.Geophysical Journal International，2006，166（1）：339-348.

［16］ Vrabie V D，Bihan N L，Mars J I.Multicomponent wave separation using HOSVD／unimodal-ICA subspace method.Geophysics，2006，71（5）：V133-V143.

［17］ Liu K H，Dragoset W H.Blind-source separation of seismic signals based on information maximization.Geophysics，2013，78（4）：V119-V130.

［18］ Bofill P，Zibulevsky M.Underdetermined blind source separation using sparse representations.Signal Processing，2001，81（11）：2353-2362.

［19］ Donoho D L，Elad M.Maximal sparsity representation viat1minimization.Proceedings of National Academy Science，2003，100（3）：2197-2202.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.005

赵彦青，萧蕴诗.基于稀疏表示的非零井源距VSP波场分离方法.石油地球物理勘探，2017，52（1）：27-33，55.

1000-7210（2017）01-0027-07

*上海市嘉定区曹安公路4800号同济大学电子与信息工程学院，201804。Email：forrest_zyq＠163.com

本文于2016年3月28日收到，最终修改稿于同年11月13日收到。

本项研究受国家自然科学基金项目（40872090）资助。

（本文编辑：宜明理）

赵彦青 博士研究生，1981年生；2002年毕业于青岛大学，获工业自动化专业学士学位；2006年毕业于同济大学，获控制理论与控制工程专业硕士学位；现为同济大学控制理论与控制工程专业博士研究生，主要从事盲信号和地震信号处理及其方法研究。