利用结构导向平滑方法解释断层

问 雪 陈雪芳 陈胜红 孟大江 唐明铭 吴 成

（中海石油（中国）有限公司深圳分公司，广东深圳518054）

利用结构导向平滑方法解释断层

问 雪*陈雪芳 陈胜红 孟大江 唐明铭 吴 成

（中海石油（中国）有限公司深圳分公司，广东深圳518054）

在深层地震资料解释过程中，受资料品质的限制，断层解释难度较大。为此，研究了对叠后地震资料进行处理的基于梯度结构张量的结构导向平滑方法，该方法能有效改善地震资料的品质，进而辅助断层解释。具体流程为：①利用原始地震数据求取每个采样点在空间（或时间）方向的导数，并求取梯度结构张量矩阵；②通过特征分解求取梯度结构张量矩阵的特征向量，并构建扩散张量矩阵；③将扩散张量矩阵代入改进的偏微分扩散方程，采用共轭梯度迭代法求解该方程，求得的解即为平滑后的图像。实际资料处理结果表明：经结构导向平滑方法处理后的地震资料信噪比有较大提高，剖面上的断点更清晰，断层的空间组合关系更明确，解释结果的可靠性更高。

断层解释 结构导向平滑 滤波 梯度结构张量 倾角扫描

1 引言

地震资料中的噪声会对解释工作造成一定影响，尤其是对深层地震资料的断层解释。因此，有必要对叠后地震数据体进行平滑滤波。常规的平滑滤波方法虽然能够很好地压制随机噪声，但是不能避免沿着断层或其他不连续体平滑，导致断层或其他不连续体的边界被模糊，从而对断层解释造成不利影响。

人们对保持构造信息和增强边界信息的地震数据平滑滤波进行了深入研究。Weichert［1-3］将扩散方程引入图像平滑中，提出了非线性扩散滤波、各向异性扩散滤波和相干增强扩散滤波。随后，Höcker等［4］、Fehmers等［5］将 Weichert的方法引入地震数据处理，推出了一种结构导向滤波方法。在此基础上，Hale［6］研究了实现方便、计算效率高的结构导向平滑方法；后来 Hale［7，8］提出了改进的结构导向双边滤波方法，并将其应用于地震图像处理。Al-Bin Hassani等［9］研究了基于多窗口分析的保护边界信息的平滑滤波方法。Wang等［10］采用基于可靠估计反射方位和边界的构造约束保边滤波法，通过扫描主频分频数据体估算反射视倾角和相干值，受噪声影响更小，估算精度更高。分频段选择性滤波［11，12］、多窗口平滑 等方法［9，11］提高 了滤波 的准确性。刘洋等［13］提出了局部相关加权中值滤波技术，并用于叠后随机噪声衰减处理，可以很好地保护地震资料中的断层等信息。赵明章等［14］利用构造导向滤波技术识别复杂断块圈闭，取得了较好的地质效果。宋建国等［15］提出了基于结构导向的梯度属性边缘检测技术，能准确地识别小断层、微裂缝，可以作为一种地震资料精细解释工具。Song等［16，17］研究了基于倾角导向Facet模型曲面拟合的边缘检测方法，并用于断层识别。刘洋等［18］提出了基于非平稳相似性系数的构造导向滤波及断层检测方法。蔡涵鹏等［19］提出了基于多窗口相干性的倾角导向主分量滤波。Cai等［20］研究了边界和振幅特性保持的自适应噪声衰减方法。尹川等［21］提出了倾角控制的构造导向滤波方法。Liu等［22］研究了基于二维希尔伯特变换的地震倾角求取方法，并用于随机噪声衰减处理。

对于构造较平缓的区域，易于提取倾角、方位角等数据，容易实现倾角导向平滑；对于复杂构造区域，很难精确求取倾角、方位角等信息，导致倾角导向平滑方法的应用效果不佳。为此，本文结合前人研究成果，研究了针对复杂构造的深层地震资料的结构导向平滑方法，对比了倾角导向平滑与结构导向平滑方法的实际应用效果。结果表明，结构导向平滑方法对地震资料信噪比的要求较低，放宽了该方法的适用条件，且更有利于提取高品质的相干体属性，而倾角导向平滑方法对地震资料的信噪比要求则很高。

2 理论基础

结构导向平滑和相干滤波的平滑系数取决于地震图像中相关构造的方位，可以通过倾角、方位角扫描获得所需要的方位信息。但是地下地质体的构造形态是未知的，在缺乏先验信息约束的情况下，倾角、方位角扫描的计算量非常大，并且精度不高。

地震图像的梯度结构张量可以提供构造的方位信息，其求取完全依赖于地震数据，具有较强的客观性。梯度结构张量的特征向量可以用于设计结构导向平滑滤波器，可以确保平滑过程沿着局部线性或者平面构造进行，而不需要跨越上述构造。

2.1 梯度结构张量

对于三维地震图像，每个采样点的梯度结构张量是一个半正定对称矩阵，可以表示为［23］

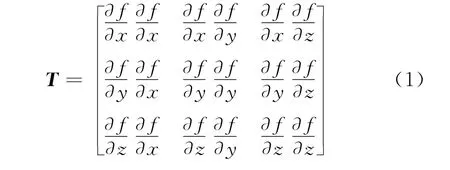
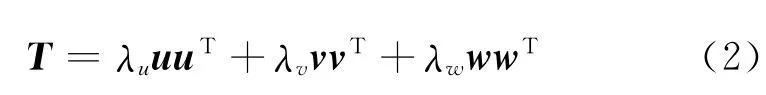
式中：λu、λv和λw为特征值；u、v和w分别表示对应的特征向量，其中u表示与构造方向垂直的分量，w表示与构造方向平行的分量。梯度结构张量矩阵为结构导向平滑提供窗口方向和窗口大小两个参数。

2.2 结构导向平滑

结构导向平滑方法的理论基础是物理学扩散过程［5］。扩散通量的表达式由菲克定律给出

式中：j为扩散通量；f为地震振幅的梯度；D为扩散张量，它是一个对称的半正定张量矩阵。

由于扩散过程中质量是守恒的，因此式（3）可以用连续性方程表示为

式中τ表示扩散时间（不同于地震记录的走时）。将式（3）代入式（4），可以得到扩散方程

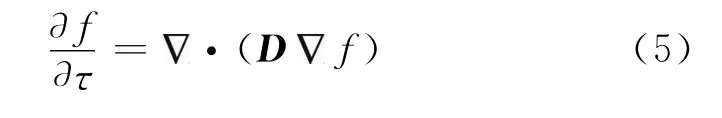
在构建扩散方程中的扩散张量D时，采用地震图像的梯度结构张量矩阵T的特征向量。

对于式（5），Hale［6］提出了一种改进的偏微分方程形式

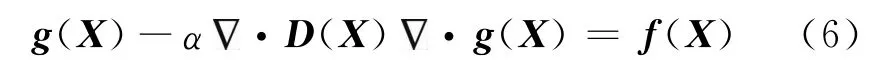
式中：f（X）（X=（x，y，z）为空间坐标）为输入的地震图像；g（X）为输出的平滑图像；D（X）为平滑后的张量矩阵；α为常量，表示平滑系数，特别地，当α=0时，g（X）=f（X），表明图像没有经过平滑。

式（6）的一维形式可以表示为［6］

采用Z变换，可以得到偏导数的双线性变换形式［6］

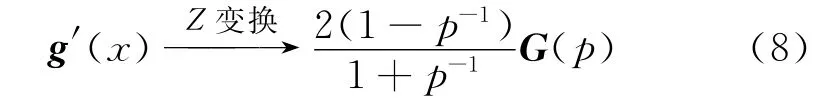
式中：g′（x）为g（x）的偏导数；G（P）为g（x）的Z变换［6］，即

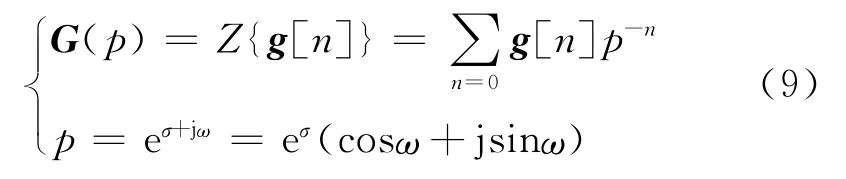
式（8）的等价形式为［6］

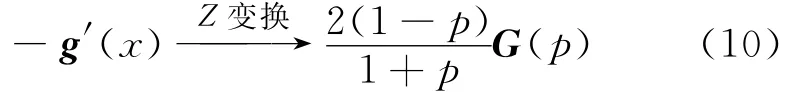
式（7）的Z变换形式为［6］

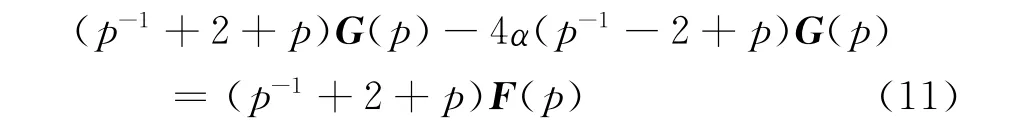
式中F（P）为f（x）的Z变换。式（11）的等价形式为

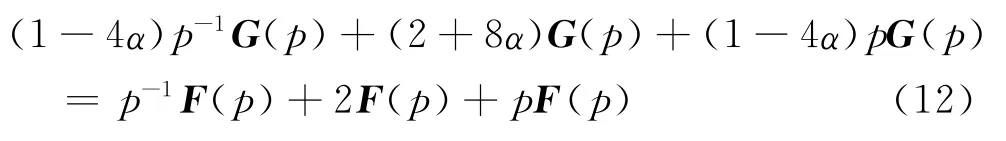
与之对应的有限差分近似式为［6］

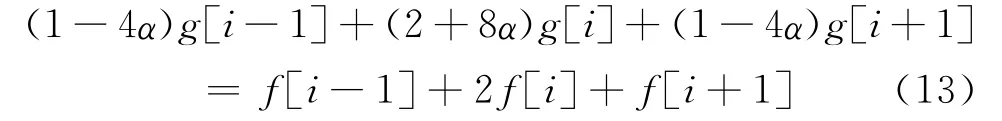
式中i=0，1，…，N-1，N表示采样点数。

对于二维或三维地震数据，可以定义向量F=f［i1，i2，…，in］表示n维输入图像f（X），定义向量g［i1，i2，…，in］表示输出的平滑图像g（X），则式（6）可以表示为［6］

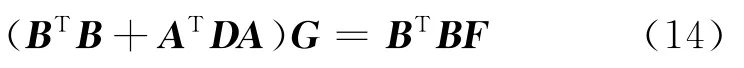
式中：稀疏矩阵A和B表示有限差分近似；D为不含零元素的系数矩阵，与式（6）中的张量矩阵D（X）对应，控制平滑方向，在结构导向平滑中采用D=vvT+wwT构建扩散张量。

采用基于梯度结构张量的结构导向平滑方法处理实际资料的具体流程如下：

（1）利用原始地震数据求取每个采样点在x、y、z（或t）方向的导数，并求取梯度结构张量矩阵T。

（2）通过特征分解求取梯度结构张量矩阵T的特征向量，并构建扩散张量矩阵D。

（3）将扩散张量矩阵D代入式（14），采用共轭梯度迭代法求解该方程，求得的解即为平滑后的图像。

3 实际应用

为了检验结构导向平滑方法的效果，针对XJ地区的地震资料开展了应用研究。研究区的主要目的层系集中在古近系，图1为目标区的原始地震剖面。由图可见，深层地震资料的品质较差，信噪比较低，断面不清晰，断层解释难度较大。图2是与图1相对应的相干体剖面。由图可见，目标区断裂发育，大断裂附近有几条伴生的小断裂，受地震资料品质的限制，断裂的空间展布特征不明显，断层组合识别难度极大。

图1 原始地震剖面

图2 相干体剖面

为了厘清目标区的断裂体系发育特征，同时检验结构导向平滑方法的有效性，本文分别采用倾角导向平滑、结构导向平滑方法对原始地震资料进行处理。图3为倾角属性剖面。由图可见，倾角变化较大的区域基本对应断裂发育区。图4为梯度结构张量的特征向量，其平行于原始地震剖面的构造方向，为结构导向平滑提供了方向约束。图5为经倾角导向平滑和结构导向平滑处理的地震剖面。由图可见，相对于原始地震剖面，经倾角导向平滑（图5a）和结构导向平滑（图5b）处理的地震剖面的信噪比都有所提高，但是后者比前者的效果更佳，对噪声的压制能力更强，尤其是在断层附近，几乎没有噪声的干扰，断点非常清晰，有利于断层解释。

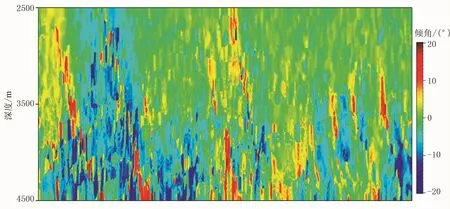
图3 倾角属性剖面

图4 梯度结构张量的特征向量

图6为对倾角导向平滑和结构导向平滑处理地震数据提取的相干体剖面。由图可见：倾角导向平滑相干体剖面对断层的显示不清晰，不能准确地描述断层的发育特征（图6a椭圆处）；结构导向平滑相干体剖面对断层的刻画更精细，断层的空间组合关系明确（图6b椭圆处），大大降低了人工解释的难度。产生这种现象的原因是：①在实际应用中，地下构造的倾角、方位角是未知的，采用倾角扫描法求取倾角、方位角属性的过程是按照一定的步长进行寻优的，这种做法会遗漏倾角、方位角的真实值，尤其是在复杂区域，很难准确求取真实的倾角、方位角；②倾角导向平滑方法对倾角、方位角的精度要求很高，当地震资料信噪比较低时，很难精确提取倾角、方位角属性。

4 结束语

基于梯度结构张量的结构导向平滑方法能够提高地震资料的信噪比，在压制噪声的过程中能有效地保留断层等不连续性信息，避免了常规平滑方法容易引起断点模糊的缺点。应用结果表明：相对于倾角导向平滑方法，结构导向平滑方法对地震资料信噪比的要求较低，放宽了该方法的适用条件；对于空间组合关系复杂的断裂带，经结构导向平滑处理得到的剖面的断点更加明确，更有利于人工解释，且由结构导向平滑处理的地震数据提取的相干体属性品质更高，断层空间组合关系更加明确。

图5 经倾角导向平滑（a）和结构导向平滑（b）处理的地震剖面

图6 对倾角导向平滑（a）和结构导向平滑（b）处理的地震数据提取的相干体剖面

［1］ Weickert J.A review of nonlinear diffusion filtering.Lecture Notes in Computer Science，Springer，1997，1252：3-28.

［2］ Weickert J.Anisotropic Diffusion in Image Processing.Teubner Verlag，1998.

［3］ Weickert J.Coherence-enhancing diffusion filtering.International Journal of Computer Vision，1999，31（2）：111-127.

［4］ Höcker C F W，Fehmers G C.Fast structural interpretation with structure-oriented filtering.The Leading Edge，2002，21（3）：238-243.

［5］ Fehmers G C，Höcker C F W.Fast structural interpretations with structure-oriented fltering.Geophysics，2003，68（4）：1286-1293.

［6］ Hale D.Structure-oriented smoothing and semblance.CWP Report 635，2009.

［7］ Hale D.Structure-oriented bilateral filtering.CWP Report 695，2011.

［8］ Hale D.Structure-oriented bilateral filtering of seismic images.SEG Technical Program Expanded Abstracts，2011，30：3596-3600.

［9］ Al-Bin Hassan N M，Luo Yi，Al-Faraj M N.3D edgepreserving smoothing and applications.Geophysics，2006，71（4）：P5-P11.

［10］ Wang Jun，Chen Yuhong and Qiao Yulei.Structureoriented edge-preserving smoothing based on accurate estimation of orientation and edges.Applited Geophysics，2009，6（4）：367-376.

［11］ Marfurt K J.Robust estimates of 3D reflector dip and azimuth.Geophysics，2006，71（4）：29-40.

［12］ Al-Dossary S，Marfurt K J.Lineament-preserving filtering.Geophysics，2007，72（1）：P1-P8.

［13］ 刘洋，王典，刘财等.局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用.地球物理学报，2011，54（2）：358-367.Liu Yang，Wang Dian，Liu Cai et al.Weighted median filter based on local correlation and its application to poststack random noise attenuation.Chinese Journal of Geophysics，2011，54（2）：358-367.

［14］ 赵明章，范雪辉，刘春芳等.利用构造导向滤波技术识别复杂断块圈闭.石油地球物理勘探，2011，46（增刊1）：128-133.Zhao Mingzhang，Fan Xuehui，Liu Chunfang et al.Complex fault-block traps identification with structure-oriented filter.OGP，2011，46（S1）：128-133.

［15］ 宋建国，孙永壮，任登振.基于结构导向的梯度属性边缘检测技术.地球物理学报，2013，56（10）：3561-3571.Song Jianguo，Sun Yongzhuang，Ren Dengzhen.Edge detection technique based on structure-directed gradient attribute.Chinese Journal of Geophysics，2013，56（10）：3561-3571.

［16］ Song Jianguo，Mu Xing，Li Zhe et al.A faults identification method using dip guided facet model edge detector.SEG Technical Program Expanded Abstracts，2012，31：1-5.

［17］ Song Jianguo，Mu Xing，Li Zhe et al.Fault identification using dip-guided facet model edge detector.Interpretation，2014，2（2）：T89-T101.

［18］ 刘洋，王典，刘财等.基于非平稳相似性系数的构造导向滤波及断层检测方法.地球物理学报，2014，57（4）：1177-1187.Liu Yang，Wang Dian，Liu Cai et al.Structure-oriented filtering and fault detection based on nonstationary similarity.Chinese Journal of Geophysics，2014，57（4）：1177-1187.

［19］ 蔡涵鹏，贺振华，李亚林等.基于多窗口相干性的倾角导向主分量滤波.石油地球物理勘探，2014，49（3）：486-494.Cai Hanpeng，He Zhenhua，Li Yalin et al.Dip-steering principal component filter using multi-window coherence scanning and interpolation.OGP，2014，49（3）：486-494.

［20］ Cai Hanpeng，He Zhenhua，Li Yalin et al.An adaptive noise attenuation method for edge and amplitude preservation.Applied Geophysics，2014，11（3）：289-300.

［21］ 尹川，杜向东，赵汝敏等.基于倾角控制的构造导向滤波及其应用.地球物理学进展，2014，29（6）：2818-2822.Yin Chuan，Du Xiangdong，Zhao Rumin et al.Dip steered structure oriented filter and its application.Progress in Geophysics，2014，29（6）：2818-2822.

［22］ Liu Cai，Chen Changle，Wang Dian et al.Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation.Applied Geophysics，2015，12（1）：55-63.

［23］ Randen T，Monsen E，Signer C et al.Three-dimensional texture attributes for seismic data analysis.SEG Technical Program Expanded Abstracts，2000，19：668-671.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.020

问雪，陈雪芳，陈胜红，孟大江，唐明铭，吴成.利用结构导向平滑方法解释断层.石油地球物理勘探，2017，52（1）：146-151.

1000-7210（2017）01-0146-06

*广东省深圳市南山区后海滨路（深圳湾段）3168号中海油大厦A座2008室，518054。Email：wenxue2＠cnooc.com.cn

本文于2016年2月23日收到，最终修改稿于同年11月17日收到。

（本文编辑：刘勇）

问雪 助理工程师，1988年生；2011年获长安大学勘探技术与工程专业学士学位；2014年获中国石油大学（华东）地球探测与信息技术专业硕士学位；现就职于中海石油（中国）有限公司深圳分公司研究院，主要从事地震解释、储层预测等方面研究。