一阶声波方程时间四阶精度差分格式的伪谱法求解

唐怀谷 何兵寿

（中国海洋大学海底科学与探测技术教育部重点实验室，山东青岛266100）

一阶声波方程时间四阶精度差分格式的伪谱法求解

唐怀谷 何兵寿*

（中国海洋大学海底科学与探测技术教育部重点实验室，山东青岛266100）

在地震波场数值模拟中，伪谱法不产生由空间网格离散引起的数值频散，而常规伪谱法用于求解时间二阶精度差分格式时，则会受到时间差分精度较低的影响而产生数值频散。本文基于一阶声波方程，提出将差分格式的时间差分精度增至四阶，并利用伪谱法求解，从而在避免由空间网格离散引起的数值频散的同时，降低由时间网格离散引起的数值频散。此外，与时间二阶精度差分格式伪谱法相比，时间四阶精度差分格式伪谱法的稳定性条件更为宽松，进而可通过增大时间网格步长提高计算效率。

一阶声波方程 数值模拟 伪谱法 时间高阶差分格式 数值频散 稳定性条件

1 引言

在地震波场数值模拟中，从声波方程或弹性波方程中求取空间导数的方法主要有伪谱法［1，2］和有限差分法［3］等。与有限差分法相比，伪谱法不会产生对空间导数项的差分引起的数值频散，因此对空间导数的求取精度更高［4］。尤其是在子波频率较高及模型中存在低速层的情况下，伪谱法在数值模拟的精度上表现出明显优势。

伪谱法虽然不产生空间差分引起的数值频散，但其数值模拟精度仍受两方面制约：一是由空间网格离散和傅里叶变换引起的吉布斯效应造成的波前畸变；另一方面是对时间导数项进行差分引起的数值频散。目前，伪谱法交错网格求解技术［5］可有效压制吉布斯效应造成的波前畸变。因此，进一步提高伪谱法数值模拟精度的关键在于降低由时间差分引起的数值频散。

地震分辨率决定于子波的频带宽度和主频［6］。然而子波主频越高，由时间差分引起的数值频散越严重，也就意味着信噪比越低。因此，在高分辨率地震勘探中，必须降低由时间差分引起的数值频散。减小时间网格步长是压制频散的方式之一，然而减小时间网格步长意味着正演到相同时间情况下增加了迭代次数，导致计算效率降低。压制由时间差分引起的数值频散的另一途径是采用高阶时间精度的差分格式进行求解［7，8］。

在一阶声波方程和一阶弹性波方程中，可将时间高阶导数项的求取转化为对空间高阶导数项的求取，从而得到任意阶时间精度的差分格式［3，9］。然而利用交错网格有限差分法对高阶时间精度差分格式进行求解，一方面对空间高阶导数的计算量非常大，另一方面其空间差分引起的数值频散相比时间差分引起的数值频散要严重得多。本文通过伪谱法求取空间导数项，在简化高阶空间导数求取的同时避免了空间差分引起的数值频散。本文基于二维情况下的一阶声波方程给出了时间四阶精度差分格式的伪谱法求解方法，该方法可以拓展到三维情况以及一阶弹性波方程。此外，本文证明了时间四阶精度差分格式伪谱法比时间二阶精度差分格式伪谱法的稳定性条件宽松，因此可以通过增大时间步长来提高运算效率。

2 一阶声波方程及其时间2M阶差分近似

在不考虑体力的情况下，各向同性介质一阶声波速度—应力方程可写成

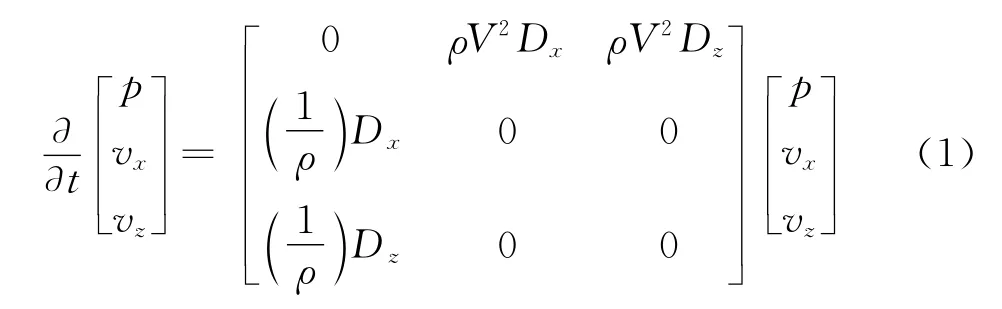
式中：D x、Dz分别为x和z方向的空间微分算子，分别表示为P为应力分量；v x和v z分别为x和z方向的速度分量。将其表示为矩阵形式

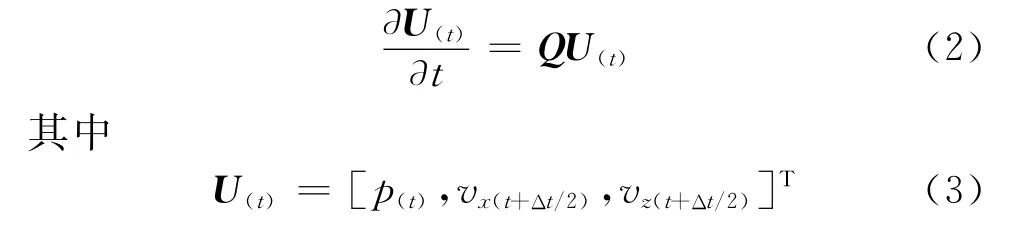
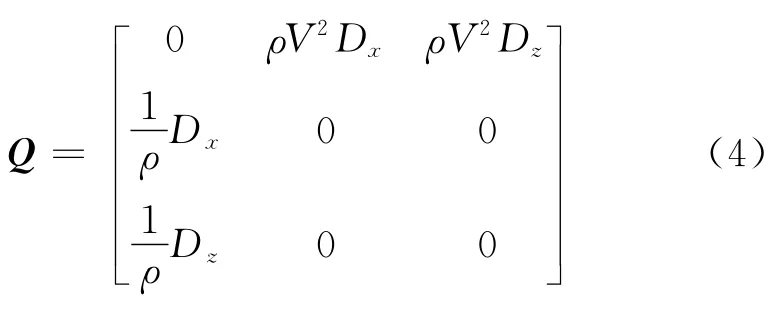
应用交错网格中心差分的思想求解一阶速度应力方程，根据一元函数的Taylor展式，得到声波方程的时间2M阶差分近似［9］

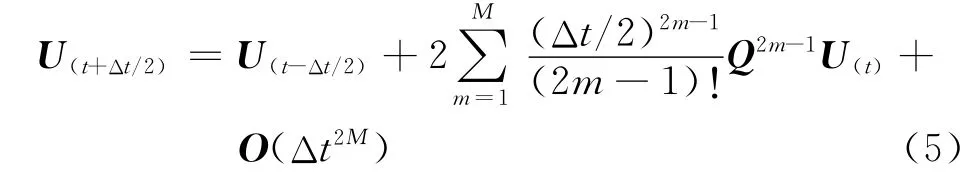
3 时间四阶精度差分格式的伪谱法

3.1 时间四阶精度差分格式及交错网格伪谱法求解

令式（5）中的M为2，则

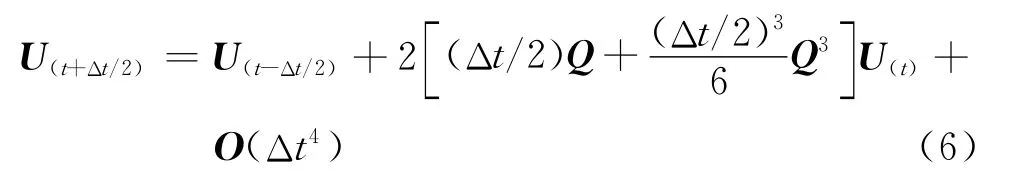
由式（4）可得

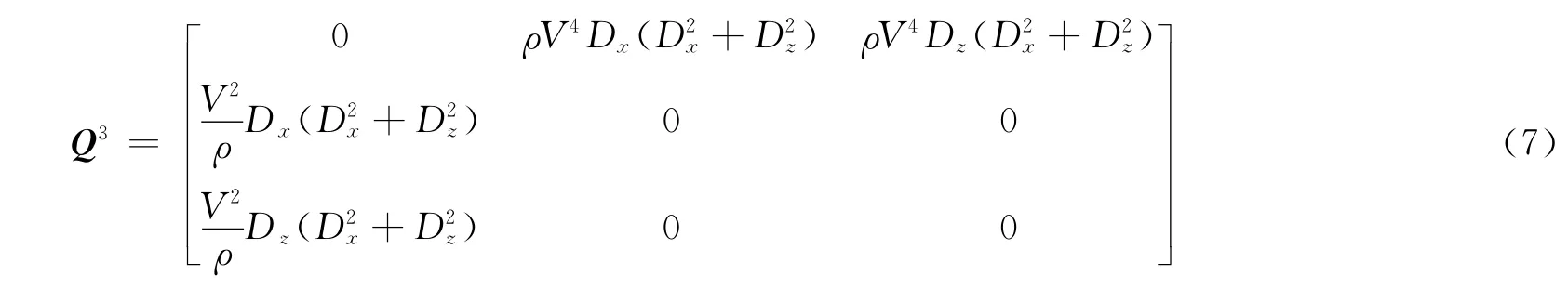
以方程形式表示式（6），得到时间四阶精度差分格式如下

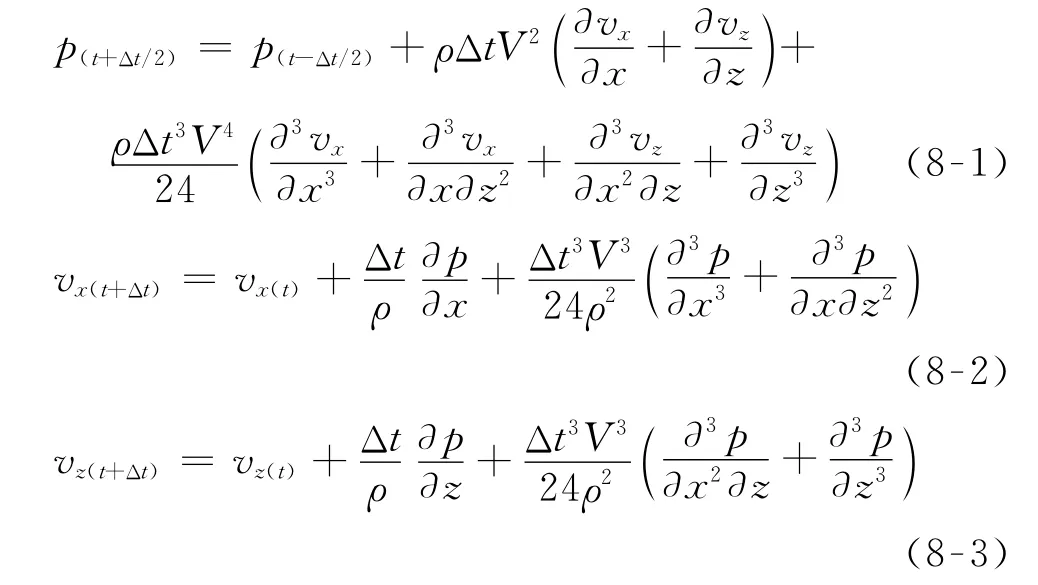
利用交错网格伪谱法［5］求解式（8）中的空间导数，其计算公式为

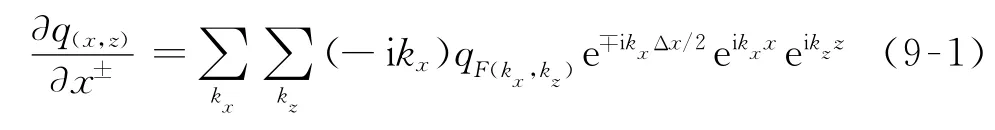
式（9）中：q指代速度分量或应变分量，q F为q的空间二维傅氏变换；k x和k z分别为x和z方向的波数；Δx和Δz分别为x和z方向的空间网格步长；±表示交错网格中不同分量之间的位置关系。将式（8）中的空间导数利用式（9）求解，得到时间四阶差分精度交错网格伪谱法计算公式为

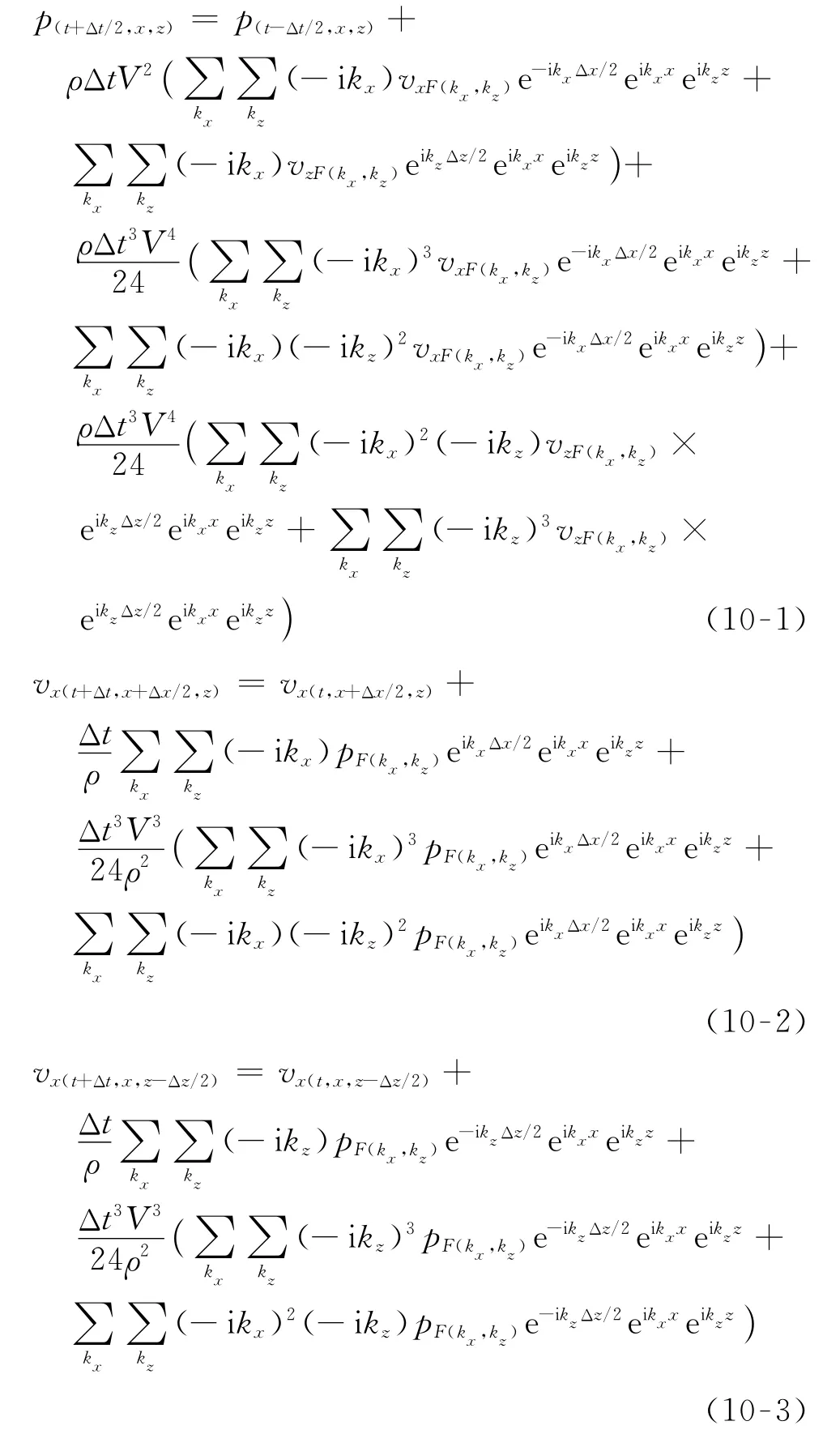
3.2 时间四阶精度伪谱法的稳定性条件和计算效率

在均匀介质中，式（10）所示的时间四阶精度差分格式的交错网格伪谱法求解格式的稳定性条件（附录B）是

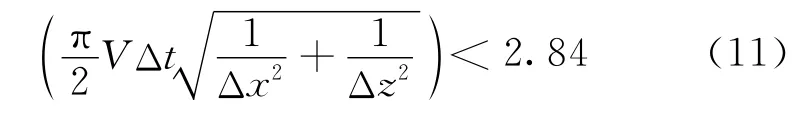
而在均匀介质中，时间二阶精度差分格式的交错网格伪谱法求解格式的稳定性条件为

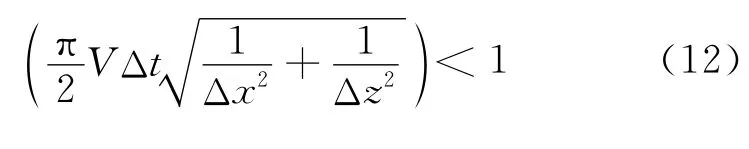
根据式（11）和式（12）的计算结果，表1列举了几种参数条件下，时间二阶精度伪谱法和时间四阶精度伪谱法满足稳定性条件的最大时间网格步长Δtmax。

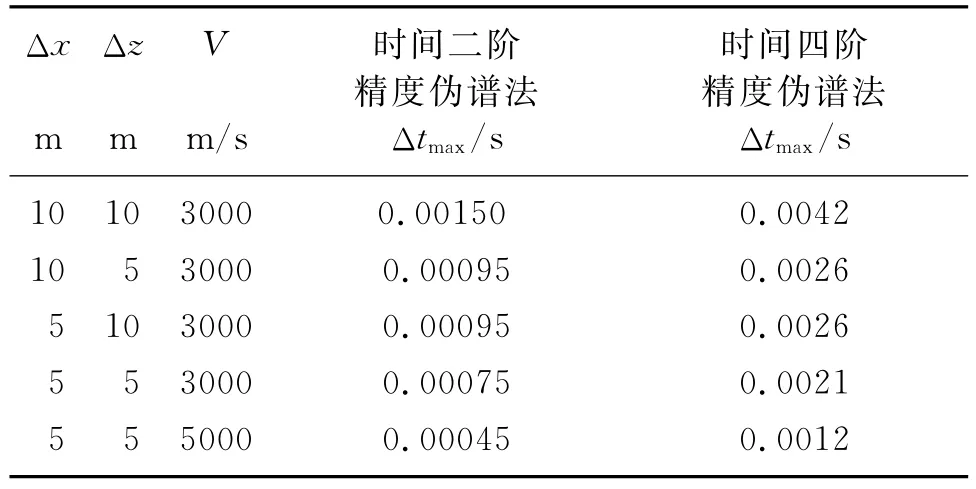
表1 伪谱法在二维均匀介质中满足稳定性条件的最大时间网格步长

在非均匀介质中，稳定性条件要苛刻一些。从表1可看出，与时间二阶精度伪谱法相比，时间四阶精度伪谱法对Δt的取值范围有显著的放宽。

在内存消耗方面，与时间二阶精度伪谱法相比，时间四阶精度伪谱法需要对三阶空间微分项进行计算。由于式（8）中对不同空间微分项的计算相互独立，且每个微分项只需计算一次，在计算空间微分项的过程中可以利用相同的内存空间进行存储。因此时间四阶精度伪谱法相比时间二阶精度伪谱法并不增加内存的消耗。

由于对规模为N x×N z的二维波场进行一次傅氏变换或反傅氏变换需要进行4（N x+N z）N x N z次乘法运算和4（N x+N z）N x N z次加法运算（附录A），因此伪谱法数值模拟的计算量主要集中在对傅氏变换和反傅氏变换的计算上，可以将正、反傅氏变换的计算次数作为评定伪谱法计算量的指标。

表2 二维情况下时间二阶差分精度伪谱法和时间四阶差分精度伪谱法进行一次迭代的傅氏变换次数

数值模拟总的计算量是迭代一次的计算量和迭代次数的乘积。从表2可见，在二维情况下，时间四阶精度伪谱法迭代一次的计算量约为时间二阶精度伪谱法的2.2倍；通过式（11）和式（12）的比较，若时间步长均取理想条件下的最大值，则时间四阶精度差分格式的时间步长可以取到时间二阶差分格式的2.84倍。因此可以通过增大时间网格步长的方式减少迭代次数，进而提高时间四阶精度差分格式伪谱法的计算效率。

3.3 时间四阶精度伪谱法的频散特性

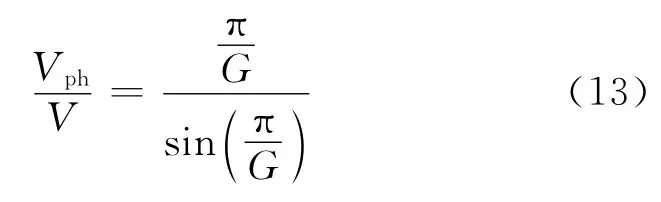
时间四阶精度伪谱法的频散关系可表示为

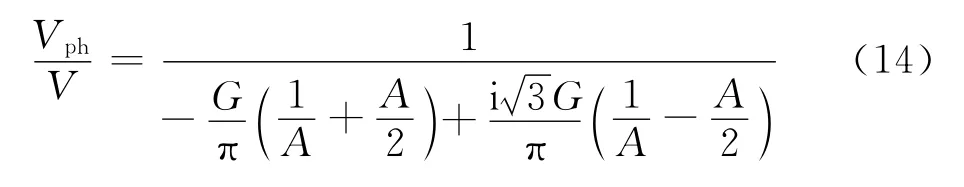
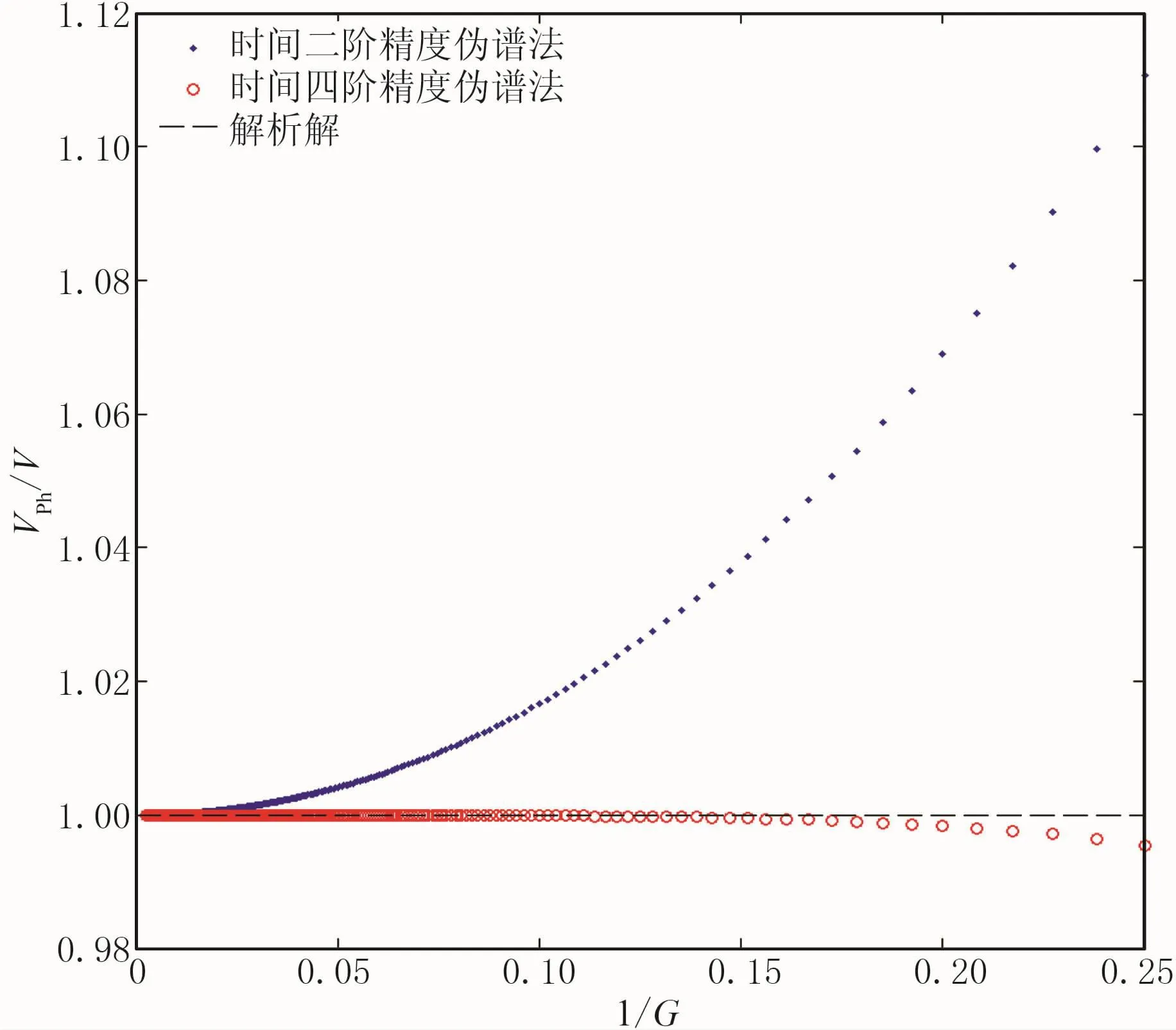
图1 时间二阶精度和时间四阶精度伪谱法频散曲线

从图1上看，时间二阶精度伪谱法的相速度超前于实际地震波速度，1／G越大则相速度与实际地震波速度之比越大；时间四阶精度伪谱法的相速度落后于实际地震波速度，1／G越大则相速度与实际地震波速度之比越小。

1／G越大则意味着一次振动包含的时间网格点数越少。对于子波中的低频成分，由于周期较长，一次振动包含的网格数较多，1／G较小，从图1中可看出，在1／G较小的情况下，时间二阶精度伪谱法和时间四阶精度伪谱法的低频成分的相速度与实际地震波速度差异均比较小；反之，对于高频成分，则1／G较大。从图1可见，在1／G较大的情况下，时间二阶精度伪谱法与时间四阶精度伪谱法相比，前者的相速度与实际地震波速度的差异远大于后者。因此，在子波主频较高的情况下，时间四阶精度伪谱法的频散特性优于时间二阶精度伪谱法。

3.4 简化的非分裂PML吸收边界条件

考虑到时间高阶差分格式存在混合偏导数，不易将波场按传播方向进行拆分，因此采用非分裂PML吸收边界条件［10］。本文对非分裂PML吸收边界条件做进一步简化，采用了一种衰减系数不随时间变化的非分裂PML边界条件。加载了边界条件的波动方程表示为

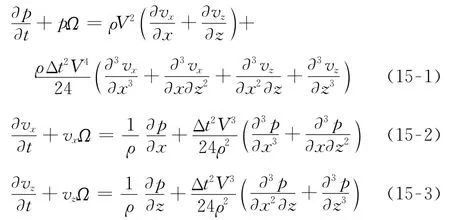
式中Ω为衰减系数，根据波场传播方向和边界位置之间的关系，将Ω分为四部分：非衰减区域、x方向边界区域（左边界区域和右边界区域）、z方向边界区域（上边界区域和下边界区域）、角部边界区域

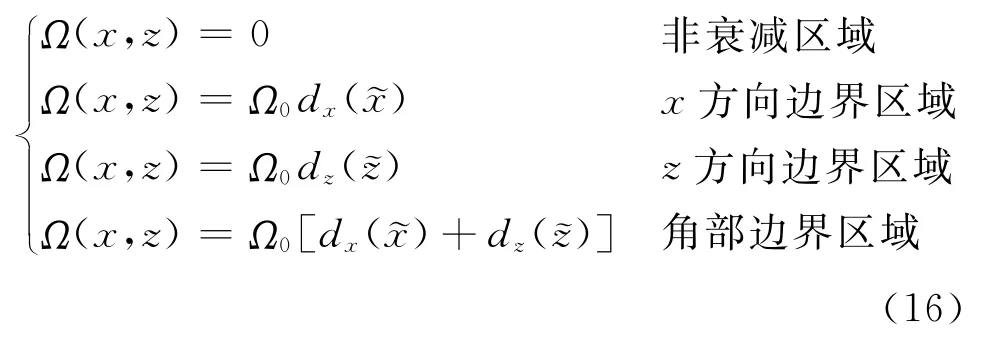
这种简化的PML吸收边界的衰减系数不随时间变化，只与位置和PML边界的厚度有关，因此衰减系数的计算简单且计算量小。加载了边界条件的波动方程不需要对波场按传播方向进行划分，而针对整体波场进行衰减，因此内存占用小。

4 模型算例及对比分析

在图2a所示的模型中，空间网格点数为200×200，空间网格步长Δx=Δz=5m。令时间网格步长Δt=0.8ms，震源位于（100，50），震源子波函数为

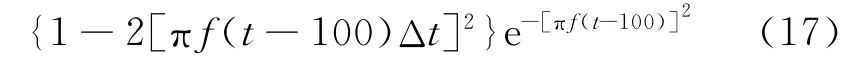
令子波主频f=80 Hz，镶嵌30层吸收边界，分别利用一阶声波方程时间二阶精度，空间十二阶精度的有限差分法、时间二阶差分精度的伪谱法以及时间四阶差分精度的伪谱法进行正演模拟，记录第400ms的波前快照。

从图2b、图2c、图2d三者的对比来看，由于波速较低，子波频率较高，图2b所示的有限差分法正演模拟结果中存在明显的数值频散，尤其是由空间差分引起的数值频散非常严重，图2c和图2d所示的伪谱法模拟结果中不含空间差分引起的数值频散。从图2c和图2d的对比来看，在子波频率较高的情况下，时间二阶精度差分格式的伪谱法正演模拟结果中仍然存在明显的由时间差分引起的数值频散，将时间差分精度提高至四阶能够有效减弱频散效应。

抽取图2b、图2c、图2d中横坐标650m、纵坐标900～1250m位置处的振动图（图3）。进一步观察波前形态，并与震源子波形态对比。可见有限差分法受空间离散影响造成的数值频散在波形上滞后于波前，二阶时间精度伪谱法受时间差分精度低的影响造成的数值频散在波形上超前于波前，四阶时间精度的伪谱法的数值频散效应显著降低，总体上数值频散的波形略滞后于波前。这与本文3.3节所述时间二阶精度伪谱法和时间四阶精度伪谱法的频散特征相符。

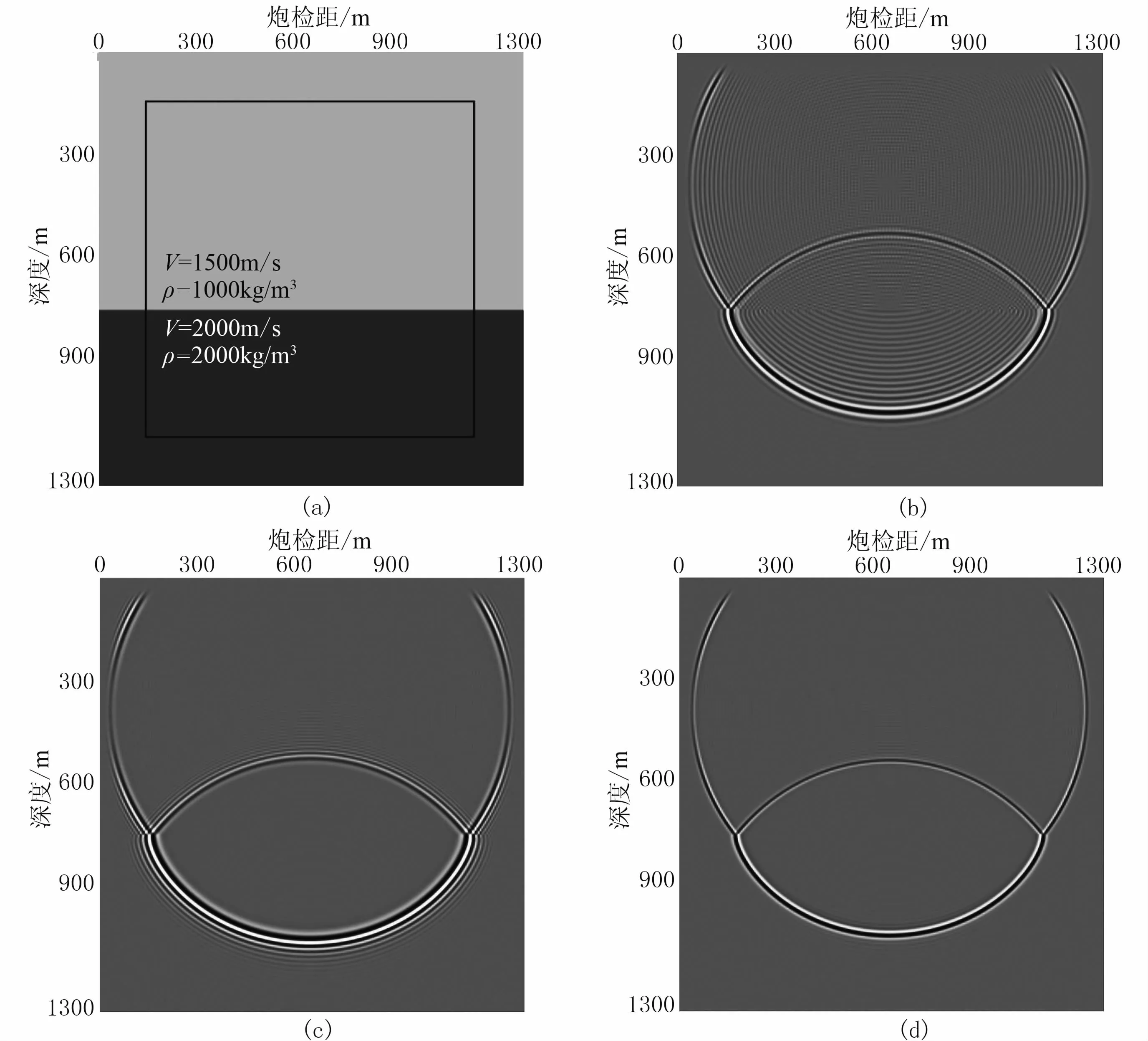
图2 含有一个反射层的层状模型及三种不同正演方法得到的波前快照

由图3可见，尽管时间四阶精度伪谱法相比时间二阶精度伪谱法的频散特性有了改善，但在子波频率较高的情况下，受时间差分截断误差的影响，时间四阶精度伪谱法的波前振动图仍然呈现一定的滞后特性。此外，子波旁瓣两侧仍有扰动，这是由吉布斯效应引起的误差。虽然使用交错网格技术可压制由吉布斯效应导致的波前畸变［5］，但由于伪谱法只能利用离散频谱求取空间导数的本质特性，将离散的波数域波场反变换回空间域必然会产生吉布斯效应。如图4所示，在子波频率较高、波场速度较低以及空间网格步长较大的情况下，伪谱法求取空间导数的精度受吉布斯效应影响较为严重。换言之，可通过降低子波主频、提高地震波速度以及减小空间网格步长三个方面减弱吉布斯效应。

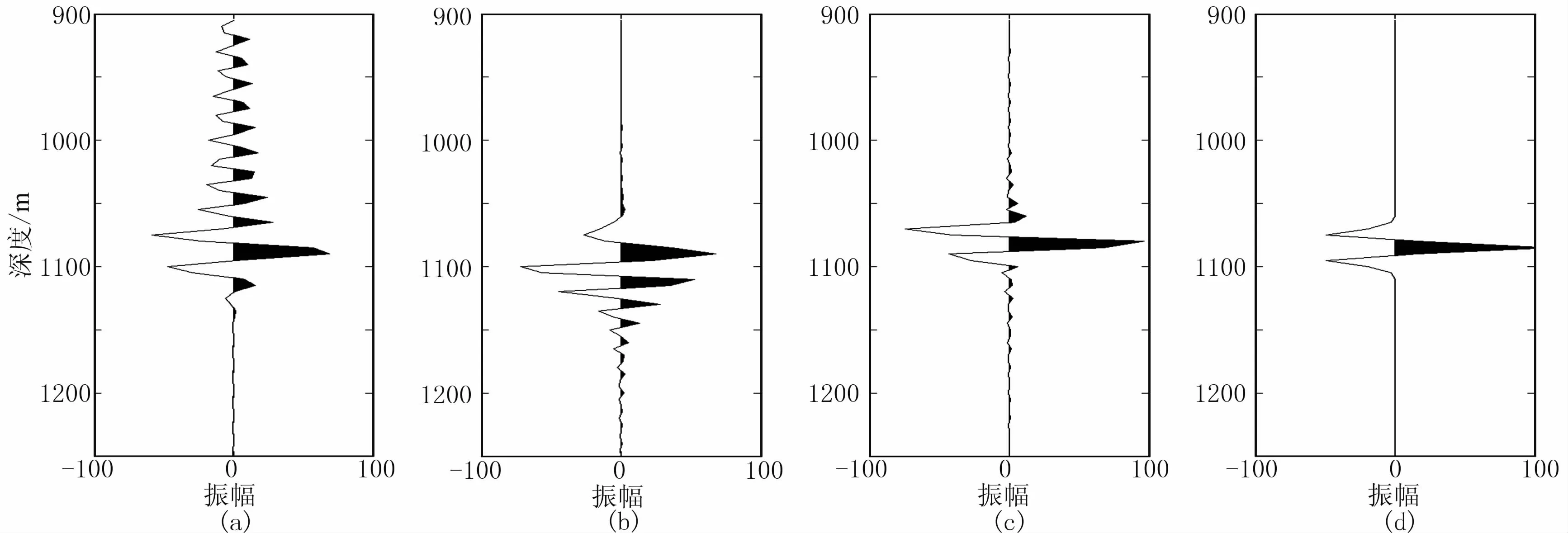
图3 抽取图2b、图2c、图2d的横坐标650m、纵坐标900～1250m位置处的振动图及震源雷克子波波形

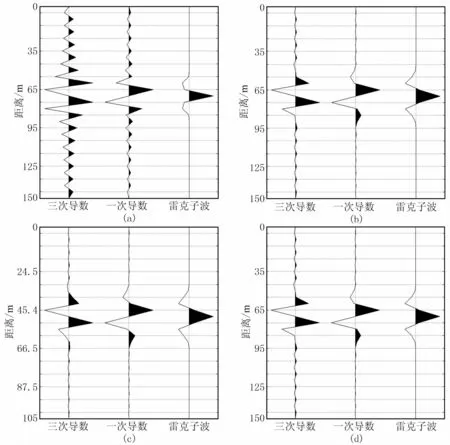
图4 不同参数条件下伪谱法求取空间导数产生的吉布斯效应比较

为进一步验证时间四阶精度伪谱法相对于时间二阶伪谱法在精度上的优势，对图5e所示水平层状模型进行正演模拟，正演模拟的参数为Δt=0.5ms，Δx=Δz=3.5，炮点位置（1250，0），f=80Hz，记录长度为700ms。通过对地震记录的比较，可观察到在子波频率较高时，时间二阶精度伪谱法的时间频散明显强于时间四阶精度伪谱法，利用时间四阶精度伪谱法得到的地震记录分辨率更高。

在Marmousi（局部）模型中分别应用上述三种方法进行正演模拟，通过图6所示地震记录的对比可见，时间四阶精度差分格式的伪谱法能够有效克服频散效应，得到的地震记录具有较高的分辨率。时间二阶精度伪谱法和时间四阶精度伪谱法的计算效率如表3所示。

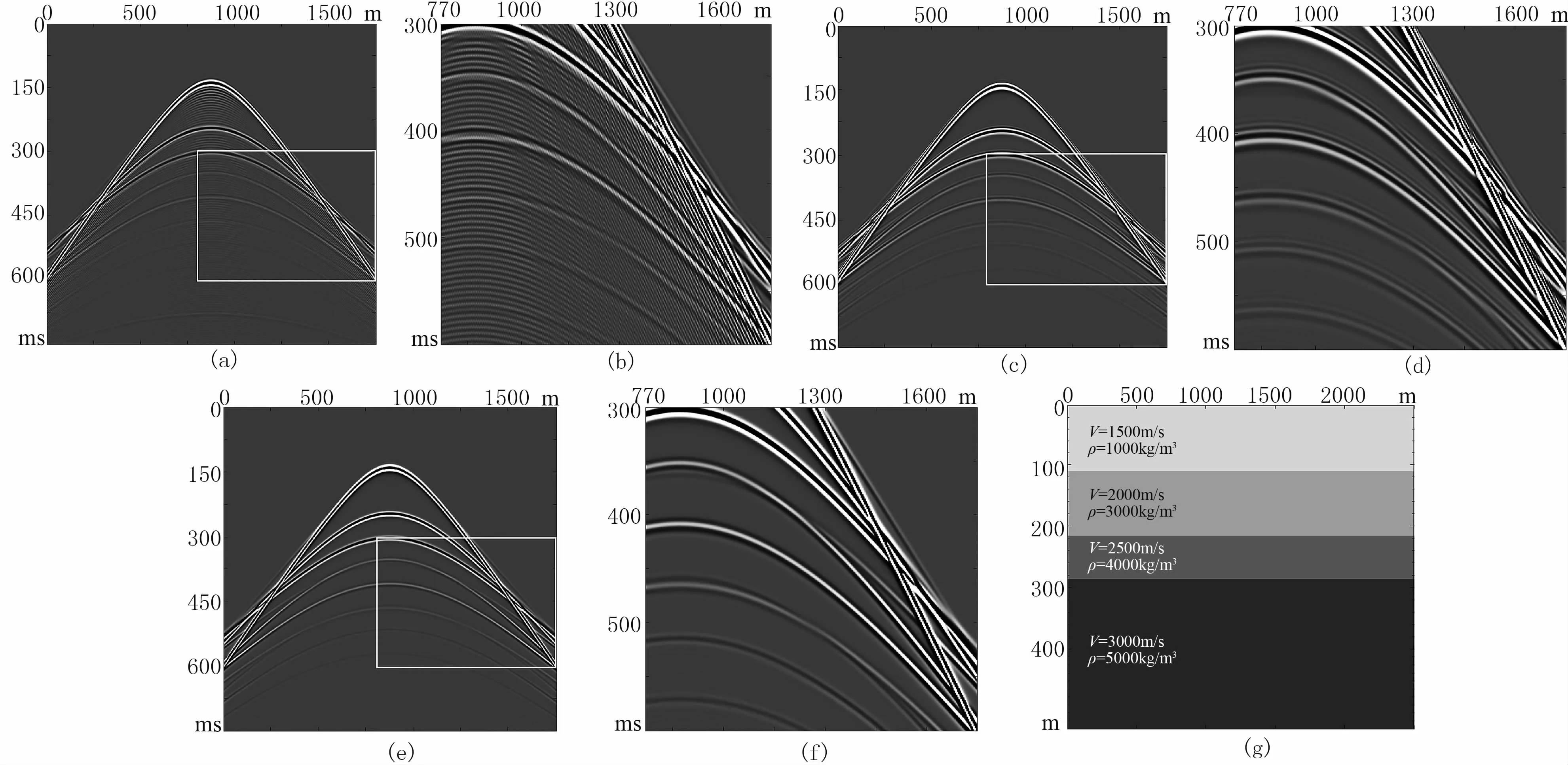
图5 有限差分法、时间二阶精度和时间四阶精度伪谱法水平层状模型地震记录

图6 利用不同正演方法对Marmousi（局部）模型得到的地震记录

表3 时间二阶精度伪谱法和时间四阶精度伪谱法的串行程序计算效率

5 结束语

通过将一阶声波方程的时间差分精度提高至四阶，在参数相同的情况下，伪谱法的数值模拟精度比时间差分精度为二阶时有显著提升，有效降低了由时间差分引起的数值频散。

时间四阶精度差分格式伪谱法迭代一次的计算量大于时间二阶精度差分格式，但时间四阶精度差分格式的伪谱法具有稳定性条件宽松的优势，因此可采用更大的时间步长以降低迭代次数，在一定程度上提高其计算效率。

感谢中国石油大学赵强博士对本文提出了建议，感谢中国海洋大学林琦博士为本文编制了图件。

［1］ Kreiss H O，Oliger J.Comparison of accurate methods for the integration of hyperbolic equations.Tellus，1972，24（3）：199-215.

［2］ Kosloff D D，Baysal E.Forward modeling by a Fourier method.Geophysics，1982，47（10）：1402-1412.

［3］ 董良国，马在田，曹景忠等.一阶弹性波方程交错网格高阶差分解法.地球物理学报，2000，43（3）：411-419.Dong Liangguo，Ma Zaitian，Cao Jingzhong et al.A staggered-grid high-order difference method of oneorder elastic wave equation.Chinese Journal of Geophysics，2000，43（3）：411-419.

［4］ Fornberg B.The pseudospectral method：Comparisons with finite differences for the elastic wave equation.Geophysics，1987，52（4）：483-501.

［5］ 杜增利，徐峰，高宏亮.虚谱法交错网格地震波场数值模拟.石油物探，2010，49（5）：430-437.Du Zengli，Xu Feng and Gao Hongliang.Pseudo spectral seismic wavefield simulation with staggered grid.GPP，2010，49（5）：430-437.

［6］ 李庆忠.走向精确勘探的道路.北京：石油工业出版社，1993.

［7］ 董良国，李培明.地震波传播数值模拟中的频散问题.天然气工业，2004，24（6）：53-56.Dong Liangguo and Li Peiming.Dispersive problem in seismic wave propagation numerical modeling.Natural Gas Industry，2004，24（6）：53-56.

［8］ 吴国忱，王华忠.波场模拟中的数值频散分析与校正策略.地球物理学进展，2005，20（1）：58-65.Wu Guochen and Wang Huazhong.Analysis of numerical dispersion in wavefield simulation.Progress in Geophysics，2005，20（1）：56-65.

［9］ 牟永光，裴正林.三维复杂介质地震数值模拟.北京：石油工业出版社，2005.

［10］ 秦臻，任培罡，姚姚等.弹性波正演模拟中PML吸收边界条件的改进.地球科学：中国地质大学学报，2009，34（4）：658-664.Qin Zhen，Ren Peigang，Yao Yao et al.Improvement of PML absorbing boundary conditions in elastic wave forward modeling.Earth Science—Journal of China University of Geosciences，2009，34（4）：658-664.

［11］ Marchuk G I.Methods of Numerical Mathematics.New York：Springer-Verlag，1975，22-30.

［12］ Irving R S.Integers，Polynomials and Rings：A Course in Algebra.New York：Springer Science ＆ Business Media，2003.

附录A 二维傅氏变换的计算量

在一维傅氏变换中，长度为N的数组x n=（x1，x2，…，x N）变换后的结果为

由式（A-1）计算一个Xm需要N次复数乘法运算和N次复数加法运算，因此长度为N的数组进行傅氏变换需要N2次复数乘法运算和N2次复数加法运算。反傅氏变换公式为

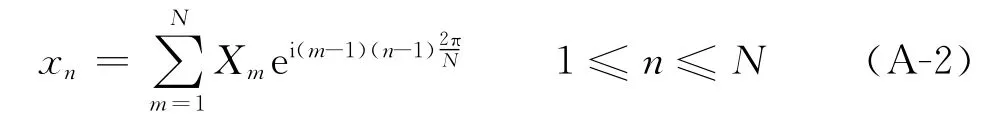
其计算量与傅氏变换的计算量相同。

对一个规模为N x×N z的矩阵进行二维傅氏变换，其过程由两次一维傅氏变换组成，即对矩阵按行（列）进行一维傅氏变换，所有的行（列）做一维傅氏变换后仍然按行（列）构成新矩阵，再对该矩阵按列（行）进行一维傅氏变换。

按行进行一维傅氏变换，即对N x个长度为N z的一维数组进行傅氏变换，计算量为次复数乘法运算和复数加法运算；同理，按列进行一维傅氏变换，即对N z个长度为N x的一维数组进行傅氏变换，计算量为次复数乘法运算和复数加法运算。因此对一个规模为N x×N z的矩阵进行二维傅氏变换或反变换的总计算量为次复数乘法运算和复数加法运算。

计算机完成一次复数乘法运算需要进行4次实数乘法运算和2次实数加法运算，完成一次复数加法运算需要2次实数加法运算。因此计算机完成一个规模为N x×N z的矩阵进行二维傅氏变换或反变换需要进行4（N x+N z）N x N z次实数加法运算和4（N x+N z）N x N z次实数乘法运算。

附录B 伪谱法求解一阶声波方程时间2M阶差分格式的稳定性条件

对式（5）进行空间傅氏变换，得到

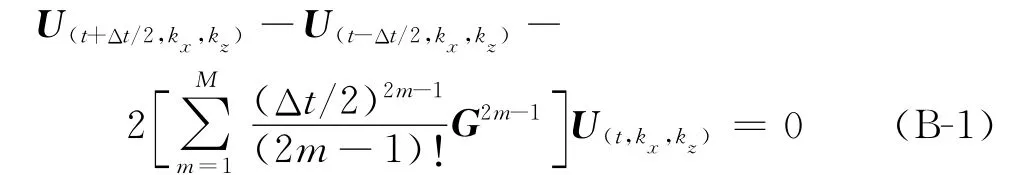
式中G（kx，kz）是Q（x，z）的傅氏变换，将U（t，kx，kz）的系数矩阵记为A，即

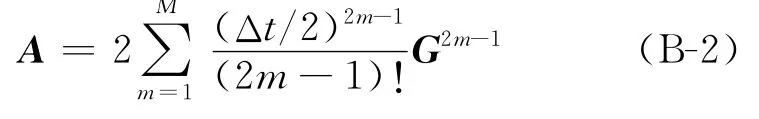
则式（B-1）可写成

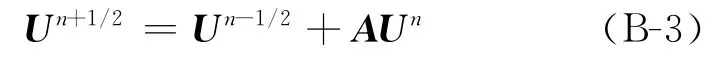
记系数矩阵A的特征值为λ，则根据傅里叶分析方法［11］可得到式（B-3）稳定的条件是A的最大模长的特征值的模小于2。

A的3个特征值为

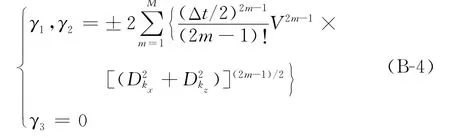
式中Dkx、D kz为空间微分算子的差分格式D x和D z的空间傅里叶变换。利用伪谱法求解式（B-3），则

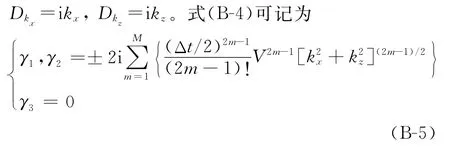
γ的模在奈奎斯特波数处取到最大值。即当k x=时，就有

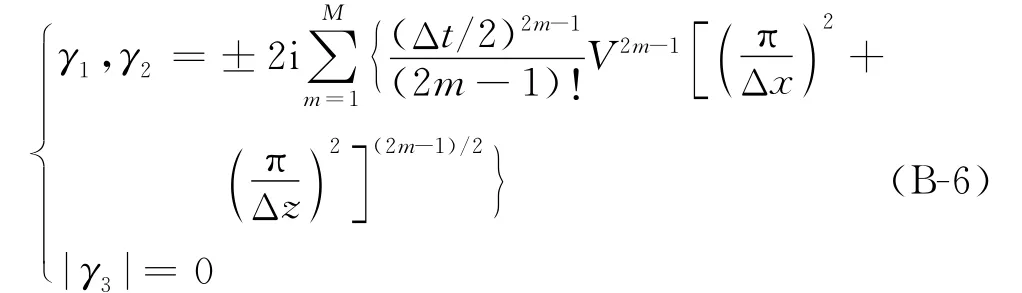
因此，利用伪谱法求解式（B-3）稳定的条件是

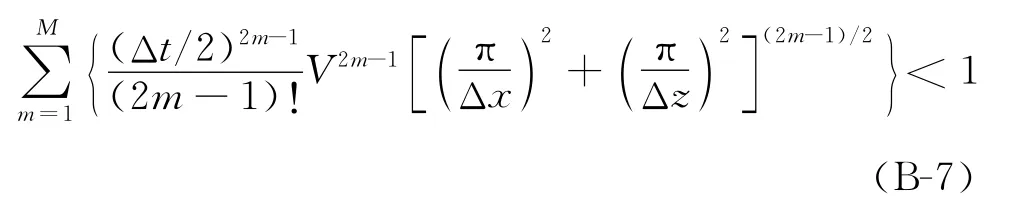
当M=1时，得到时间二阶精度的稳定性条件，即式（11）；当M=2时，得到时间四阶精度的稳定性条件，即式（12）。

附录C 一阶声波方程伪谱法频散特性

伪谱法求解时间二阶精度声波方程的差分格式为

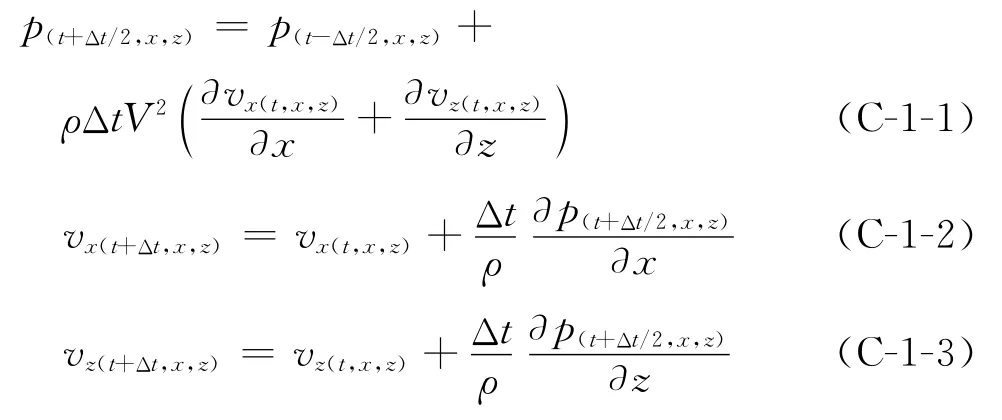
设一阶声波方程P分量简谐波形式的解析解为

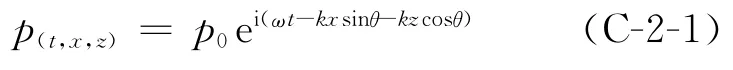
式中：θ为P的传播方向x与z方向的夹角；ω为角频率（ω=2πf），f为频率；k为波数λ为波长，则有为相速度。

将式（C-2-1）分别代入式（C-1-2）和式（C-1-3）中，得到v x和v z的解析解为

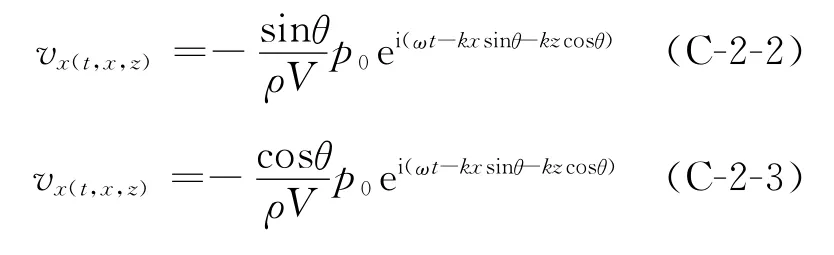
将式（C-2）代入式（C-1-1）中，得到

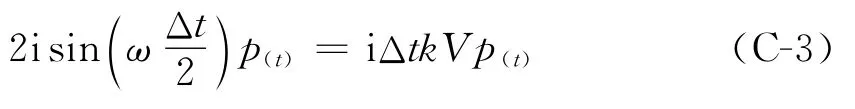
该式等号两端同时除以ω，进一步整理得到

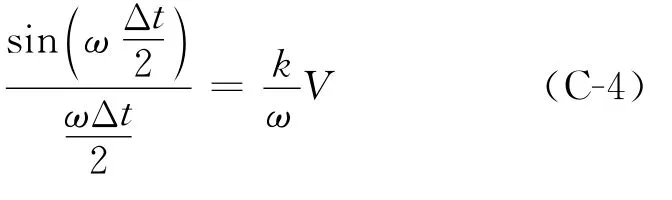
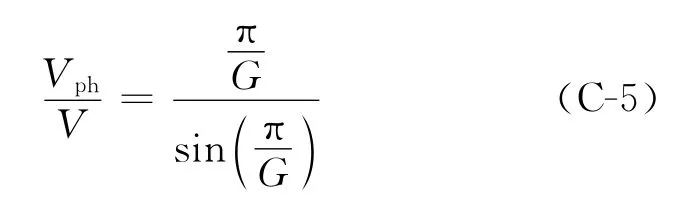
将式（C-2）代入式（C-1-2）中，得到

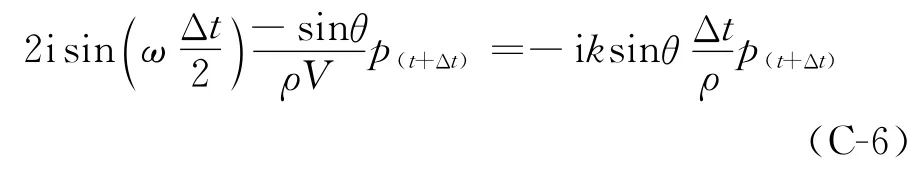
同理，将式（C-2）代入式（C-1-3）中，得到

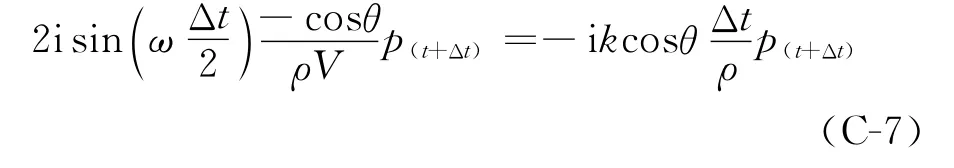
在式（C-6）和式（C-7）的等号两端同时除以ω，做进一步整理，对应地可得到式（C-4）和式（C-5）。因此，时间二阶精度差分格式伪谱法满足式（C-5）所描述的频散关系。

求取时间四阶精度差分格式的频散特性，将式（C-2）代入式（8-1）中，得到

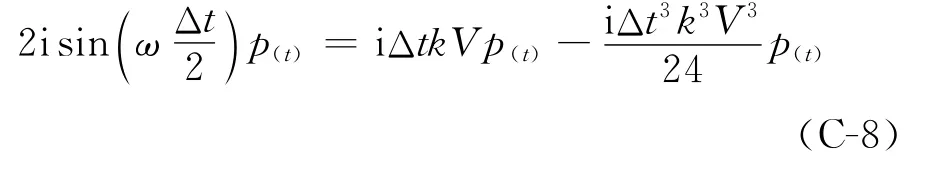
经过化简，得到

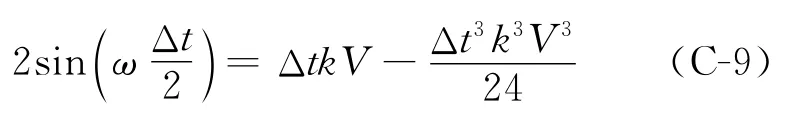
进一步可写为

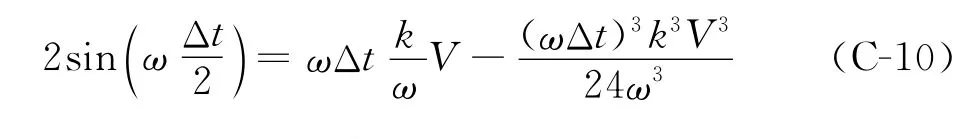
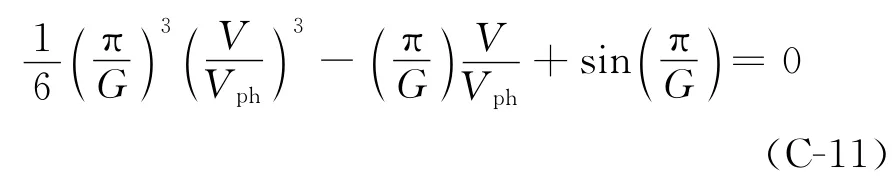
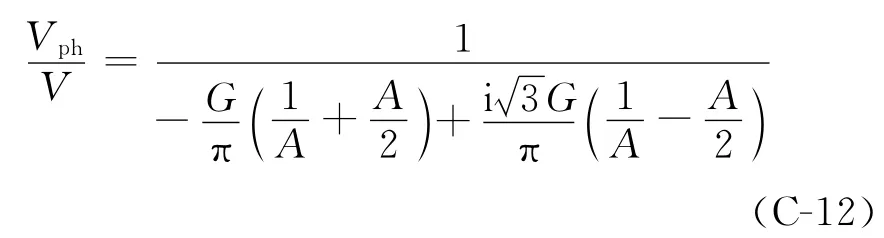
P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.011

唐怀谷，何兵寿.一阶声波方程时间四阶精度差分格式的伪谱法求解.石油地球物理勘探，2017，52（1）：71-80.

1000-7210（2017）01-0071-10

*山东省青岛市中国海洋大学海底科学与探测技术教育部重点实验室，266100。Email：hebinshou＠ouc.edu.cn

本文于2015年12月23日收到，最终修改稿于2016年12月18日收到。

本项研究受国家自然科学基金项目（41174087）和“863”项目（2013AA064201）资助。

（本文编辑：朱汉东）

唐怀谷 硕士研究生，1992年生；2014年本科毕业于中国海洋大学勘查技术与工程专业，获工学学士学位；现在该校海洋地球科学学院攻读地球探测与信息技术专业硕士学位。