紊流环境下四维轨迹优化的伪谱方法研究
李创, 刘小雄, 马青原, 薛鹏飞
(西北工业大学 自动化学院, 陕西 西安 710072)
紊流环境下四维轨迹优化的伪谱方法研究
李创, 刘小雄, 马青原, 薛鹏飞
(西北工业大学 自动化学院, 陕西 西安 710072)
为了提高紊流条件下飞机的飞行安全,提出了一种基于伪谱方法的四维轨迹优化方法。建立了不确定环境中的飞机动力学模型和紊流模型,并设计了目标函数和约束条件;通过伪谱法将不确定环境下的四维轨迹优化问题转化为非线性优化问题,然后应用序列二次规划对该问题进行求解;讨论了不同的配点数对优化结果的影响,分析比较了GPM,LPM和RPM三种伪谱法的特点。仿真结果表明,紊流情况下,所提算法可以精确地找到四维飞行轨迹。
紊流; 四维轨迹优化; 伪谱法; 序列二次规划
0 引言
随着社会的发展,人们对航空运输的需求激增。欧美等国家为了缓解本区域航空运输压力、减少航班延时、使机场吞吐量达到最大,推出了“下一代空中交通运输系统实现计划(NextGen)”,并提出了基于4D轨迹的管理(4DTBO)[1],飞行器轨迹优化作为计划的核心之一而备受关注。四维轨迹优化技术[2]在传统的三维空间上加上时间维的信息,为飞机在空域中流动量扩增提供了可能,同时还保证了整个飞行阶段内飞机飞行的安全性。
紊流是造成航空失事的主要因素之一。四维轨迹优化必须考虑飞行过程中飞机遭遇紊流和雷暴天气问题。Matsuno等[3]提出了一种广义多项式混沌算法,将之应用到飞机飞行避撞;但是其求解繁琐且计算时间较长。近年来,伪谱法因其求解最优控制问题具有收敛速度快、收敛区间广、精度高等特点受到青睐,早期主要用于解决噪声主动控制问题[4-6]。Elnagar等[4]将Legendre伪谱方法应用于普通微分方程描述的非线性系统求解。Ross等[7]则利用Legendre伪谱法求解直接轨迹优化及非光滑的最优控制问题。文献[8-9]提出Gauss伪谱法,并证明了非线性规划问题的KKT条件与离散形式的HBVP问题一阶最优性必要条件具有一致性。
本文将紊流规避四维轨迹优化问题转化为最优控制问题,建立了Gauss伪谱法、Legendre伪谱法、Radau伪谱法的数值计算方法,并结合序列二次规划(Sequential Quadratic Programming,SQP)方法求解轨迹优化问题。
1 紊流规避问题建模
1.1 飞机模型
考虑到数值解法在求解最优控制问题时首先要考虑解的收敛速度,需要将飞机运动方程[10]无量纲化处理,得到无量纲化模型为:
(1)
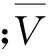
在此模型中,用于飞机横侧向控制的滚转角φ和用于飞机纵向控制的Nz组成了控制变量组。
1.2 风场模型
利用风速随高度增加而变化的线性模型来描述风场变化规律:

1.3 紊流模型
利用高斯分布来描述紊流强度:
式中:z(t)=(x,y,H)为飞机位置信息;σ为紊流影响范围;(μx,μy,μH)为紊流影响的中心位置。
1.4 约束条件
在四维轨迹优化问题中,将已知的初始点状态作为初始条件。当飞机到达终端时,所有的状态信息是提前预设的,尤其要求飞机的到达时间必须满足要求,因而终端条件也是给定的。边界条件为:
考虑飞机安全性、乘客的舒适性以及飞机舵面的偏转限制,对飞机的航迹角、航向角、滚转角和过载进行限制。路径约束为:
1.5 目标函数
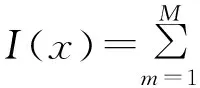
2 伪谱法求解紊流规避问题
2.1 应用伪谱法将问题转化为NLP问题
伪谱法一般将Gauss正交节点作为函数积分、微分和插值的离散节点。通过简单的线性变换,可以很容易地将实际问题中的时间区间[t0,tf]转化到正交节点所在的区间。其中Gauss伪谱法(GPM)、Legendre伪谱法(LPM)以及Radau伪谱法(RPM)较常见,都是同时对控制变量和状态变量进行全局逼近,其区别仅在于配点的选取。
(1)LG配点(Legendre-Gauss)
LG配点选取方法为:
R(u)=0,u(t)∈P2N+1(t∈[-1,1])
(2)LGL配点(Legendre-Gauss-Lobatto)
LGL配点选取方法为:
R(u)=0,u(t)∈P2N-1(t∈[-1,1])
(3)LGR配点(Legendre-Gauss-Radau)
LGR配点选取方法为:
R(u)=0,u(t)∈P2N(t∈[-1,1])
式中:PN为最高次数为N的代数多项式的集合;LN(t)为N阶Legendre多项式。
三种伪谱法主要区别在于配点选择,求解步骤基本一致。以Gauss伪谱法为例,介绍连续型最优控制问题转化为非线性规划问题的具体步骤。
Step 1:时域变换。将时域[t0,tf]转换到区间[-1,1]。转换关系为:
Step 2:计算LG配点。输入GPM配点数N,计算LG配点(配点数为N,离散节点数为N+2),即N阶Legendre多项式的根,记为PN(t)。
Step 3:计算微分矩阵、积分权重。无权重微分矩阵表示为:
其中:
式中:τk(k=1,…,N)为LG配点;τi(i=0,…,N)为LG配点加上初始值点。
另外,LG配点对应的Gauss正交权重为:
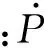
Step 4:将状态微分方程在节点按照GPM离散化方程进行离散化(终端状态单独近似离散化)。
写成微分矩阵表示的离散化状态方程为:
其中:
注意,在边界值上没有进行离散化。所以要对终端边界点处的状态变量进行单独的离散化处理,必须增加一个约束条件以保证终端状态Xf满足状态方程。这可以用一个正交多项式近似在整个时间间隔上的状态积分来实现:
Step 5:Bolza型性能指标离散化。
根据Gauss积分公式,Bolza型性能指标公式中的Lagrange项的积分部分可以表示为:
式中:wk为Gauss积分权重。Meyer项可以表示为:
显然,Bolza型性能指标离散化形式可表示为:
Step 6:边界条件和路径约束离散化。边界条件可以表示为:
路径约束在LG配点上的离散化形式为:
2.2 应用SQP求解
SQP方法对原问题的近似中包含有二阶导数信息,在保持全局收敛性的同时具有局部超线性收敛,是一种求解光滑非线性规划问题的优良算法。其基本思想是,在某个近似解处,将待求解的非线性规划问题近似为处理一个二次规划问题,求最优解。求解步骤为:
Step 1:给定初始解x0∈Rn,初始正定Hessian矩阵B0∈Rn×n(通常设置为单位阵),容许误差限为0≤ε<1;取参数σ>0,δ>0;设置k=0。
Step 2:求解二次规划子问题,得到dk;如果‖dk‖≤ε,跳出算法,dk为最优解,否则继续执行。
Step 4:迭代格式为xk+1=xk+αkdk;同时计算f(xk+1),f(xk+1),c(xk+1),Ak+1。
Step 6:利用拟牛顿法更新近似Hessian矩阵Bk+1,设置修正量为sk=αkdk,并使:
yk=xL(xk+1,λk+1)-xL(xk,λk+1)
Step 7:令k=k+1,执行第二步。
3 仿真试验及结果分析
以本文飞机模型为对象,利用伪谱法和SQP方法求解紊流规避四维轨迹优化问题。仿真条件为:
(1)在惯性坐标系中,假设紊流中心位置为(μx,μy,μH)=(-20,0,2)n mile,紊流影响区域假定为以紊流中心为球心的球体,影响范围为σ=1.5 n mile。
(2)从初始位置(x0,y0,H0)=(-40,0,0)n mile出发,初始航迹角γ0=0°,初始航向角χ0=0°;在规定时间tf=330 s时,到达终端位置(xf,yf,Hf)=(0,0,4.5)n mile,终端航迹角γf=0°,终端航向角χf=0°。
(3)路径约束:H∈[0,6.5]n mile,Nz∈[0,1.5g],γ∈[-89°,89°],χ∈[-180°,180°],φ∈[-60°,60°]。
分别用上述三种伪谱方法解决紊流规避四维轨迹优化问题。为了提高求解精度,伪谱法选择离散节点数目自然越多越好。但是由于飞机动态方程复杂、变量数目较多,离散节点个数的增加必然导致算法计算时间的增加,选取12个离散化节点求解紊流规避四维轨迹优化问题。三种伪谱方法的目标函数计算结果基本相同,求解精度差别不大,在计算时间上RPM略微优于GPM和LPM。仿真结果如图1和图2所示。

图1 紊流规避四维优化轨迹Fig.1 4D optimal trajectories for turbulence avoidance
由图1可以看出,采用三种伪谱方法生成的优化轨迹均可以成功地避开紊流影响区域,曲线比较光滑且彼此差异不大。这是因为三种伪谱方法在进行离散化逼近时所遵循的原理是相近的,区别仅表现在积分节点、权重和微分矩阵的不同,从而导致了优化结果的些许差异。

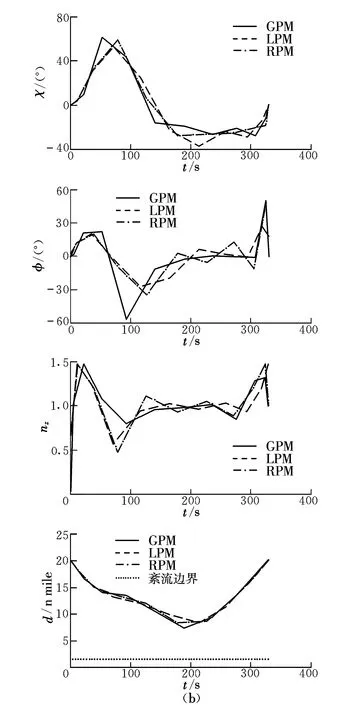
图2 三种伪谱法仿真结果Fig.2 Simulation results of three pseudo-spectra methods
图2中,d为距紊流的距离。可以看出,三种伪谱法的计算结果均满足约束要求,飞机始终处于紊流影响范围外,达到了紊流规避目的。
4 结束语
紊流规避轨迹优化问题是一个非线性最优控制问题,运用数值解法可以精确、快速地得到优化解。以紊流规避问题为研究对象,利用Gauss伪谱法、Legendre伪谱法、Radau伪谱法分别对其进行数值求解,结果满足性能要求。由优化结果可知,Radau伪谱法和Gauss伪谱法相对于Legendre伪谱法计算效率更高。对于复杂、多变量的非线性问题,可以使用伪谱方法进行求解,表明了伪谱方法在轨迹优化方面的应用价值。
[1] Zhao Yiyuan,Vaddi S.Algorithms of FMS reference trajectory synthesis to support nextgen capability studies[R].AIAA-2013-4264,2013.
[2] Battipede M,Sirigu G,Cassaro M,et al.Analysis of the impact of performance model accuracy on 4D trajectory optimization[R].AIAA-2015-0145,2015.
[3] Matsuno Y,Tsuchiya T.4D trajectory optimization in the presence of uncertainty[R].AIAA-2013-4323,2013.
[4] Elnagar G,Kazemi M,Razzaghi M.The pseudospectral legendre method for discretizing optimal control problems[J].IEEE Transactions on Automatic Control,1995,40(10):1793-1796.
[5] Huntington G T,Rao A V.Optimal reconfiguration of spacecraft formations using the Gauss pseudospectral method[J].Journal of Guidance,Control,and Dynamics,2008,31(3):689-698.
[6] Banks H T,Fakhroo F.Legendre-Tau approximations for LQR feedback control of acoustic pressure fields[J].Journal of Mathematical Systems Estimation and Control,1998,8(4):393-426.
[7] Ross I M,Fahroo F.Legendre pseudospectral approxi-mations of optimal control problems[M]//Kang W,Borges C,Xiao M Q.New trends in nonlinear dynamics and control and their applications.Vol 295.Berlin:Springer Berlin Heidelberg,2004:327-342.
[8] Benson D.A Gauss pseudospectral transcription for optimal control[D].Massachusetts:Massachusetts Institute of Technology,2005.
[9] Benson D A,Huntington G T,Thorvaldsen T P,et al.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1435-1440.
[10] Smith N E,Cobb R G,Pierce S J,et al.Optimal collision avoidance trajectories via direct orthogonal collocation for unmanned/remotely piloted aircraft sense and avoid operations[R].AIAA-2014-0966,2014.
(编辑:李怡)
Four-dimension trajectory optimization for turbulence avoidance using pseudo-spectra methods
LI Chuang, LIU Xiao-xiong, MA Qing-yuan, XUE Peng-fei
(School of Automation, Northwestern Polytechnical University, Xi’an 710072, China)
To improve the flight safety of aircraft in the presence of turbulence, 4D trajectories optimization based on pseudo-spectra method was proposed. Considered the characteristic of 4D trajectories optimization for turbulence avoidance, aircraft dynamic model and turbulence Gaussian distribution model were elaborated, the objective function and constraints were designed. The 4D trajectories optimization was transformed into a nonlinear programming issue by using pseudo-spectra method, and the sequential quadratic programming (SQP) algorithm was applied to resolve this nonlinear programming problem. Influence of the collocation points on optimization results was discussed, and the characters of the pseudo-spectra methods such as GPM, LPM and RPM were analyzed. Simulation results show that the 4D trajectories for turbulence avoidance can be generated accurately using the proposed algorithm.
turbulence; 4D trajectory optimization; pseudo-spectra method; sequential quadratic programming
2016-05-09;
2016-09-14;
时间:2016-11-10 09:10
航空科学基金资助(20150753009);西北工业大学研究生创意创新种子基金资助(Z2016146)
李创(1992-),男,陕西渭南人,硕士研究生,研究方向为飞行控制与轨迹优化; 刘小雄(1973-),男,陕西周至人,副教授,博士,研究方向为飞行控制与仿真、轨迹优化与四维制导。
V249.1
A
1002-0853(2017)01-0025-05

