平面应变条件下含孔洞土样受内压作用的变形破坏过程

王学滨，田锋，董伟，侯文腾，余斌

(辽宁工程技术大学 a.计算力学研究所；b.力学与工程学院，辽宁 阜新 123000)

在土木、水利及油气存储等工程中，一些洞室常受内压作用，例如，水工涵洞表面和油气存储腔体表面[1-2]。研究受内压作用洞室周围岩土体的变形破坏规律对于有关灾害的机理分析及预防具有重要理论及实际意义。

针对含孔洞模型或试样的室内实验是研究洞室周围岩土体变形、破坏规律的重要手段之一。这方面已经有大量文献报道，其结果通常比数值模拟和理论研究可靠性更高。

在现有针对含孔洞模型或试样的室内实验研究中，模型或试样多为单轴应力状态，孔洞通常不受内压作用，而实际工程中受内压作用洞室周围岩土体处于三维应力状态，一般可简化为平面应变模型进行力学研究。此外，目前，基于DIC方法的针对含孔洞模型或试样的变形、破坏过程分析多为根据云图的定性、粗略分析，缺乏定量、统计分析。

本文利用自主研制的平面应变模型加载及观测系统，开展了不同加载速率条件下含孔洞土样双轴压缩实验。利用DIC方法获得土样的位移场，利用能较好滤掉位移场噪声的局部位移最小二乘拟合方法[8]获得最大剪切应变的分布及演变规律。为了定量获得最大剪切应变和分析方便，根据清晰剪切带位置，布置曲折测线和平直测线，对各测线上最大剪切应变进行统计分析，深化了对含孔洞土样变形及破坏规律的认识。

1 土样制备、实验及计算

1.1 土样制备

实验用土取自某高层建筑工地距地表5 m处，液限wL=42.20%，塑限wP=25.22%，为低液限黏土。含孔洞土样的制备采用固结法，其过程为：1)将土干燥后碾碎，并过孔径0.5 mm的筛子；2)将土和水按照质量比3∶1进行混合，充分搅拌成塑性状态，注入模具；3)待模具中土体固结并干燥至一定程度后，拆除模具，制成约10 cm×10 cm×4.7 cm的长方体土样；4)在长方体土样的最大表面中心处沿与该面垂直的方向钻直径3 cm的通孔，制成含孔洞土样(简称为土样)；5)选择一个含孔洞土样，在表面均匀涂抹白色颜料薄层，待晾干后，在白色表面随机喷涂直径为4～10像素的黑色斑点，以满足黑色斑点直径为4～10像素时散斑图质量较好的要求[9]。

1.2 实验过程

首先，将土样置于自主研制的平面应变模型加载装置(图1)内的中间底垫块上，在土样上方放置垂直应力加载垫块，其前、后尺寸与土样前、后尺寸一致，而左、右尺寸略小于土样左、右尺寸，并将左、右侧压加载板置于左、右底垫块之上；其次，将前、后玻璃板分别置于土样的前、后方，且玻璃板的两侧卡在侧箱内壁上，使玻璃板与土样表面贴合，以确保土样处于平面应变状态；其次，将内囊通过后玻璃板中心孔放入土样孔洞内，并将侧囊放入侧箱，安装侧箱顶板；其次，用螺栓连接侧箱与连接板，以限制侧箱的水平运动，保证侧囊施加的侧压保持水平；最后，将侧囊、内囊的气嘴与高压管线相连，通过气瓶对其充气，以实现对土样左、右表面及孔洞表面施加侧压和内压。土样上、下表面的压力(垂压)由试验机施加，通过调节试验机下压头的移动速率，即加载速率，实现对不同土样进行位移控制加载。在土样变形过程中，通过操控数码相机对土样喷涂了散斑的表面图像进行拍摄，每幅图像的大小为2 112像素×

图1 平面应变模型加载系统示意图Fig.1 Schematic of the loading system under plane

2 112像素。在对土样施加内压和侧压后、进行位移控制加载前，操控数码相机对土样喷涂了散斑的表面图像开始进行拍摄，以记录土样在位移控制加载过程中的全部变形过程。为了便于DIC方法的应用，在土样表面出现明显宏观裂纹时停止实验。在相同实验条件下，进行3～5个土样实验，共进行70余个土样的实验，从中选出内压、侧压和含水率条件类似且加载速率不同的4个土样进行研究，即56#、17#、2#及8#土样，以获得剪切带发生、发展过程受加载速率的影响规律。各土样的基本参数及实验条件见表1。

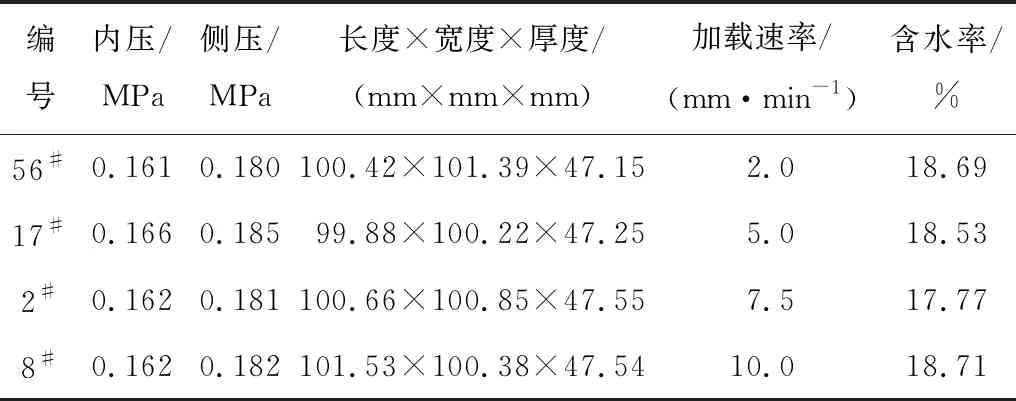
表1 土样的基本参数及实验条件Table 1 Basic parameters and experimental conditions of clay specimens

1.3 应变场的计算

首先，利用基于Newton-Raphson迭代的DIC方法[10]获得各测点的位移；然后，利用局部位移最小二乘拟合方法(简称为最小二乘拟合方法)获得应变。

基于Newton-Raphson迭代的DIC方法求位移的步骤为：首先，对物体变形前后的两幅散斑图像进行亚像素插值；然后，在给定位移初值后，通过反复计算Hessian矩阵的逆矩阵和Jacobian向量对位移进行更新。当相关系数满足阈值时，停止更新，此时的位移即为所求测点的位移。

最小二乘拟合方法求应变的步骤为：首先，在已知位移场的情况下，以各测点(间隔为Δ)为中心选择一个局部子域(即应变计算窗口)，见图2，对应变计算窗口的位移进行一次多项式拟合，获得位移函数；然后，对位移函数进行求导，获得各测点的应变。

有关计算参数如下：子区尺寸为31像素×31像素，测点间隔Δ为10像素，应变计算窗口大小为5测点×5测点(M=2，相当于41像素×41像素)，56#、17#、2#及8#土样中布置的测点数目分别为16 383(127行×129列)、16 383(127行×129列)、17 161(131行×131列)、16 002(126行×127列)个。

最大剪切应变(γmax)为标量，常用于表征应变局部化现象，其与水平线应变εx、垂直线应变εy及剪切应变γxy有关[11]。

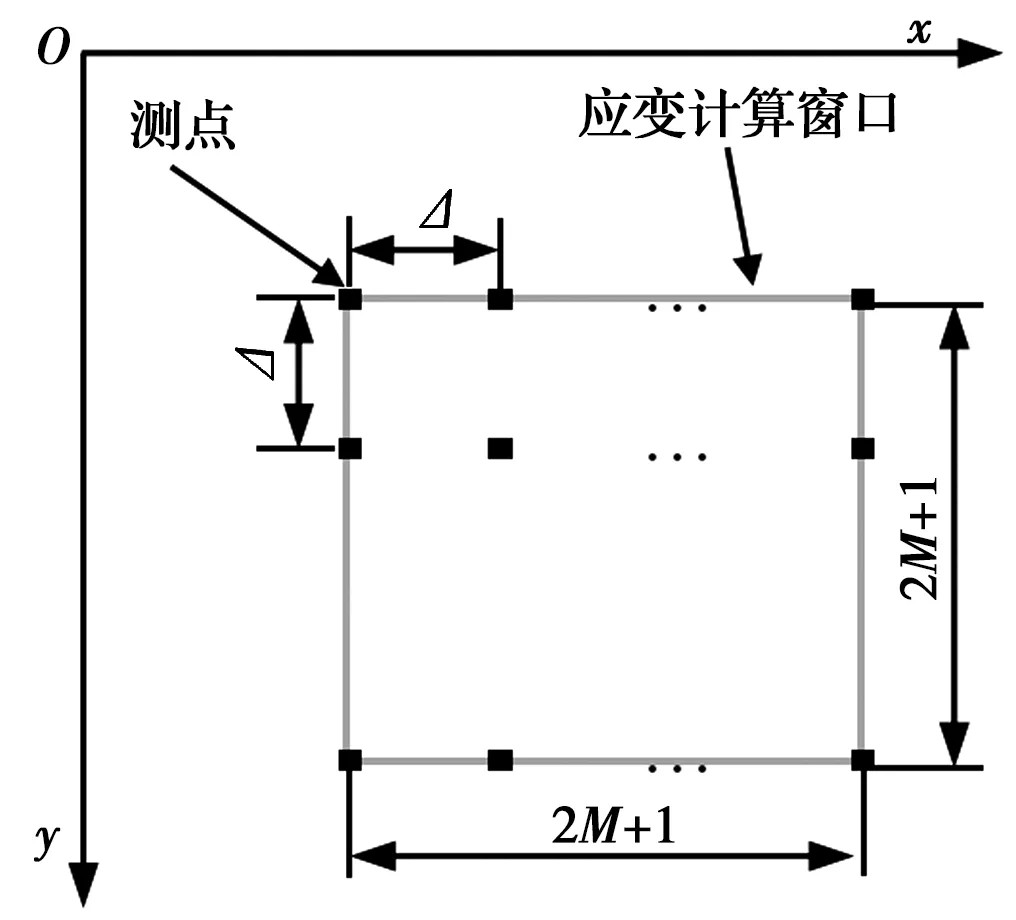
图2 测点周围的应变计算窗口Fig.2 Calculating window around a monitored

2 实验结果分析

2.1 纵向应力纵向应变曲线

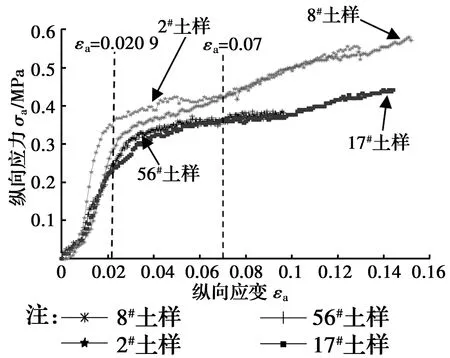
图3 土样的εa-σa曲线Fig.3 Stress-strain curves of clay

由图3可以发现，4个土样均经历了两个阶段：近似线性阶段和硬化阶段。由于土样表面出现明显宏观裂纹时即停止实验，所以，土样未来得及经历明显的软化阶段。在近似线性阶段，各土样的σa-εa曲线变化规律几乎类似，但在εa相同时，2#土样的σa较其他土样高，且在εa=0.020 9时便开始进入硬化阶段，这可能与其含水率稍低有关，土样稍硬；在硬化阶段，在εa相同时，加载速率较大的土样σa较高，这与常识相符。

2.2 土样γmax的分布及演变规律

图4和图5给出了56#和8#土样不同εa时γmax的分布规律(各子图左方和下方的数字分别代表各测点的行数和列数)，文中涉及的其他土样破坏过程与此类似，限于篇幅，不再赘述。可以发现：

图4 56#土样不同εa时γmax的分布Fig.4 Distributions of γmax for different εaof the clay specimen

图5 8#土样不同εa时γmax的分布Fig.5 Distributions of γmax for different εaof the clay specimen

1)随着εa的增加，γmax的分布经历了近似均匀变形向局部化变形的转化过程。在土样加载初期，γmax呈斑点状随机分布，且γmax较小(图4(a)和图5(a))，可以近似地认为土样变形均匀。当应变较小时，DIC的计算结果容易出现奇异点，土样中即使有应变集中，奇异点也会对此现象有所掩盖。应当指出，由于未对施加内压和侧压之前的土样进行拍摄，所以，DIC的计算结果中不包括由内压和侧压引起的应变集中。随着εa的增加，出现了多块或多条模糊、宽阔的应变不均匀分布区域(图4(b)～(d)和图5(b)～(d))，并进一步发展成1～2条清晰、狭窄的应变强烈集中区域，即剪切应变局部化带(剪切带)(图4(f)和图5(f))，导致土样发生破坏。

2)γmax的演变规律较为复杂，最终的1～2条清晰的剪切带是由多块或多条应变不均匀分布区域通过竞争发展而成的，有时难以事先判断出来。

56#土样剪切带的发展演化过程如图4所示，当εa=0.005 3时，γmax的分布呈斑点状随机分布，且γmax较小，土样的变形基本上是均匀的。由图4可以发现，当εa≤0.030 4时，土样处于近似线性阶段。当εa=0.015 9时，由孔洞顶部偏右和底部偏左各发展出了一条高角度应变局部化带，相比之下，孔洞底部偏左的较长，土样仍处于近似线性阶段。随着εa的增加，上述两条高角度应变局部化带进一步发展，土样仍处于近似线性阶段。当εa=0.039 8时，孔洞顶部偏右的高角度应变局部化带变得不清晰，在孔洞左帮偏上、右帮偏上和左帮偏下各发展出了一条模糊的且较宽阔的应变不均匀区域。此时，土样已进入硬化阶段。当εa=0.047 1时，孔洞的顶部偏右和底部偏左的高角度应变局部化带变得更不清晰。当εa=0.060 4时，孔洞右帮偏上的应变不均匀区域发展成通过土样右上角的剪切带，孔洞左帮偏下的应变不均匀区域发展成另一条剪切带，并导致土样最终发生“/”形剪切破坏。

8#土样剪切带的发展演化过程如图5所示。土样处于近似线性阶段及之前的现象不再赘述。当εa=0.023 0时，在孔洞左帮偏上、右帮偏上、左帮偏下及右帮偏下发展出了较不清晰的应变不均匀区域，土样仍处于近似线性阶段。当εa=0.039 4时，上述4块应变不均匀区域的应变进一步发展。此时，土样已进入硬化阶段。当εa=0.069 0时，孔洞左帮偏上的应变不均匀区域发展成通过土样左上角的剪切带，孔洞右帮偏下的应变不均匀区域发展成另外一条剪切带。当εa=0.091 9时，上述两条剪切带的应变进一步发展。当εa=0.137 9时，两条剪切带变得更清晰，并导致土样最终发生“”形剪切破坏。

应当指出，由图4和图5仅能定性地描述剪切带的发展演化规律。为此，下文将通过布置测线的方式进一步揭示剪切带的发展演化规律。

2.3 测线的布置

由图4(f)和图5(f)可以发现，狭长且最终导致土样发生剪切破坏的剪切带并非笔直。为了能捕捉到剪切带发展过程中剪切带行进路线上不同位置的γmax，有必要布置曲折测线。同时，为了比较剪切带内、外γmax的不同，有必要在上述曲折测线之外布置测线。

分别选择56#土样孔洞顶部偏右的高角度应变局部化带A、17#土样右帮偏上的剪切带B、2#土样左帮偏上的剪切带C及8#土样右帮偏下的剪切带D布置测线(图6)。平直测线与曲折测线的线性拟合结果平行。同时，建立直角坐标系sos′，s轴与一条平直测线重合，s轴正向指向孔洞。应当指出，曲折测线是根据狭长剪切带的最终位置确定的。56#、17#、2#及8#土样中的曲折测线分别命名为A0、B0、C0及D0，两侧的平直测线分别命名为A1和A2、B1和B2、C1和C2及D1和D2。

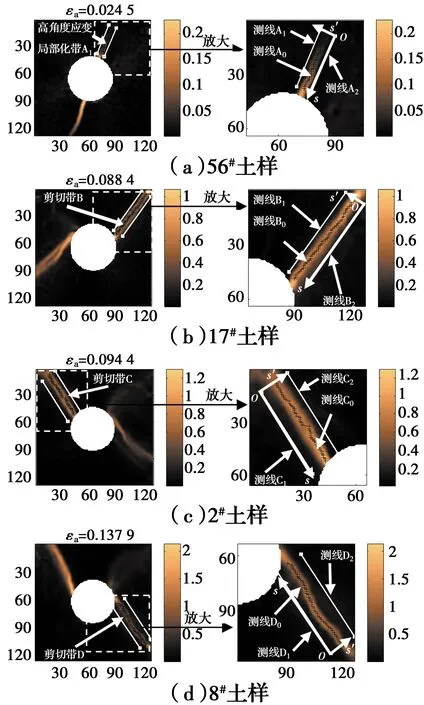
图6 剪切带内外测线的位置Fig.6 Positions of monitored lines in shear bands and

2.4 测线上γmax的分布、演变规律及统计

图7～图10分别给出了4个土样不同εa时各测线上γmax-s曲线。图11给出了56#土样不同εa时测线A0上εx-s、εy-s及γxy-s曲线。

图7 56#土样不同εa时测线A0、A1及A2上γmax-s曲线Fig.7 γmax-s curves at monitored lines A0, A1 and A2for different εa of the clay specimen

图8 17#土样不同εa时测线B0、B1及B2上γmax-s曲线Fig. 8 γmax-s curves at monitored lines B0, B1 and B2for different εa of the clay specimen

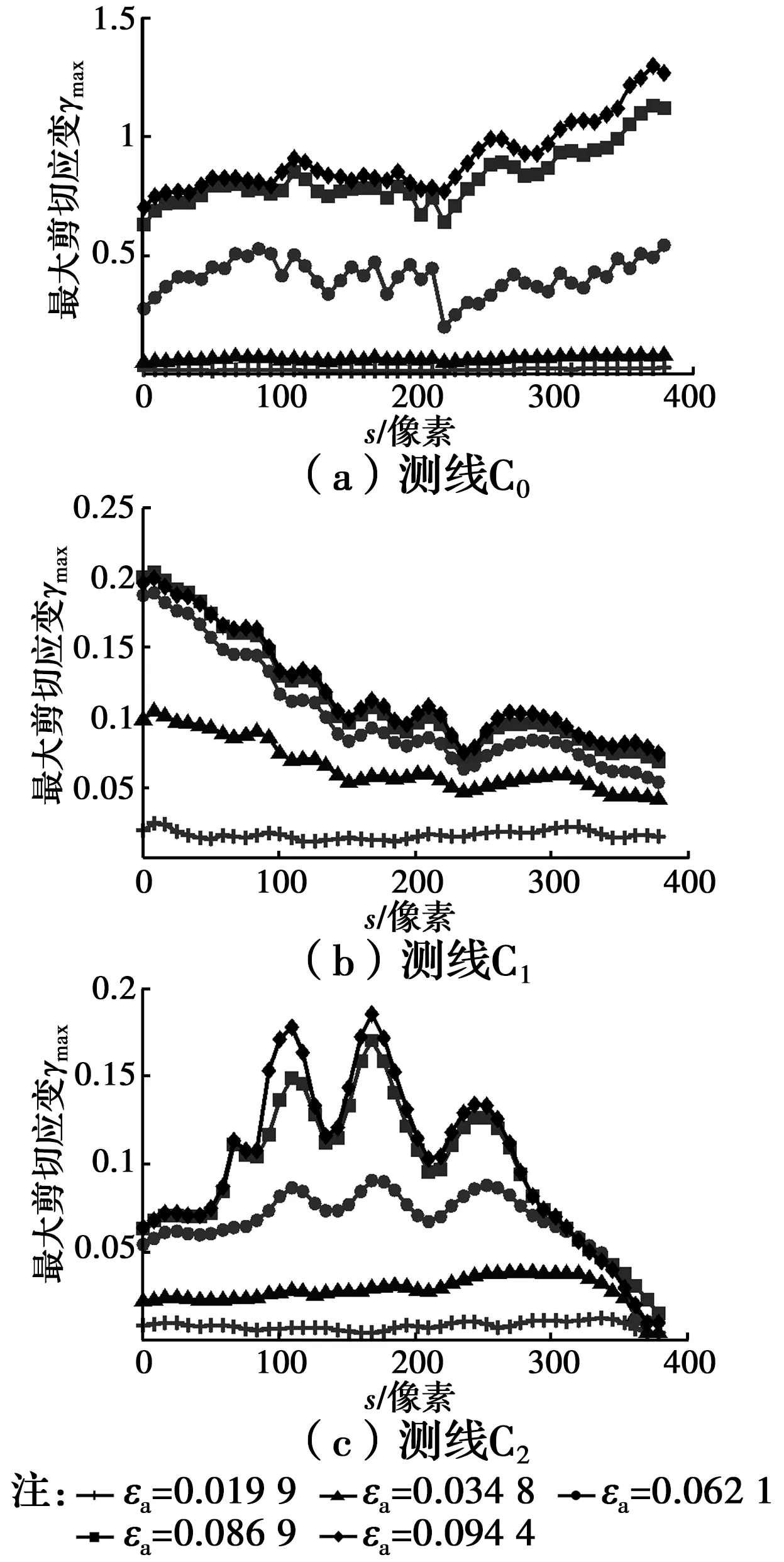
图9 2#土样不同εa时测线C0、C1及C2上γmax-s曲线Fig.9 γmax-s curves at monitored lines C0, C1 and C2for different εa of the clay specimen

图10 8#土样不同εa时测线D0、D1及D2上γmax-s曲线 Fig.10 γmax-s curves at monitored lines D0, D1 and D2for different εa of the clay specimen

图11 56#土样不同εa时测线A0上εx-s、εy-s及γxy-s曲线Fig.11 εx-s curve, εy-s curve and γxy-s curve at the monitored line A0 for different εa of the clay specimen

对于56#土样(图7)，当εa=0.005 3时，测线A0及两侧测线A1和A2上γmax的分布较均匀，且γmax较小。当εa=0.015 9时，测线A0、A1及A2上γmax的均值分别为0.028 5、0.010 0及0.006 5。显然，测线A0上γmax远大于测线A1和A2，这说明孔洞顶部偏右的高角度应变局部化带已经形成。此时，离孔洞表面越近(s越大离孔洞表面越近)，测线A0上γmax越大，这说明孔洞顶部偏右的高角度应变局部化带是从孔洞表面向外发展的。当εa=0.024 5时，与εa=0.015 9时相比，测线A0上γmax有所增加。当εa=0.039 8时，与εa=0.024 5时相比，测线A0上γmax下降，这说明在上述过程中高角度应变局部化带上的应变正在释放。由图11可以发现，当εa=0.039 8时，与εa=0.024 5时相比，测线A0上各测点的εx、εy及γxy均下降了，相比之下，εx下降得更明显，说明上述高角度应变局部化带是由拉破坏导致。当εa≥0.039 8时，随着εa的增加，测线A0上大部分测点的γmax有上升趋势。对于测线A1，随着εa的增加，不同εa时测线A1的γmax波动均较大，变化复杂。对于测线A2，随着εa的增加，测线A2上大部分测点的γmax逐渐增加。例如，当εa从0.039 8增至0.060 4时，测线A2上s=192.1像素处γmax从0.019 05增至0.039 56。

对于17#土样(图8)，当εa=0.025 0时，测线B0及两侧测线B1和B2上γmax的分布较均匀，且γmax较小。当εa=0.048 4时，与εa=0.025 0时相比，测线B0、B1和B2上γmax的分布不均匀。此时，随着向孔洞表面的靠近，测线B2上γmax有增大的趋势。此时，随着向孔洞表面的靠近，测线B1上γmax先下降后上升；在离孔洞较远位置，测线B1与土样右上角的应变不均匀区域相交，因受该区域的影响较大，导致离孔洞较远位置的γmax较大；对于孔洞附近的测点(s≥330像素)，随着向孔洞表面的靠近，测线B1上γmax有下降趋势，这应与剪切带外弹性应变降低(卸荷)有关。当εa=0.059 2时，测线B0上γmax分布不均匀，此时，测线B0上γmax几乎都比测线B1和B2上的大；在离孔洞较远位置，测线B0上γmax较大，这应与土样右上角的破坏有关，剪切带B由土样右上角向孔洞发展；随着向孔洞表面的靠近，测线B2上γmax先下降后有上升趋势，在离孔洞较远位置，测线B2与剪切带B相交，测线B2上γmax受剪切带B的影响较大，导致离孔洞较远处的γmax较大；在s=120.7像素处γmax出现了高峰，这应与该测点附近出现的剪切带分叉现象有关；对于孔洞附近测点(s≥313.9像素)，随着向孔洞表面的靠近，测线B2上γmax有下降趋势，这应与剪切带外弹性应变降低(卸荷)有关。当εa=0.076 7时，对于孔洞附近测点(s≥281.7像素)，随着向孔洞表面的靠近，测线B0上γmax有上升趋势，这可能是由于越靠近孔洞表面，γmax集中越严重。此时，与εa=0.059 2时相比，剪切带有变陡趋势，在离孔洞较远的位置，剪切带位置变化不大，而在离孔洞较近的位置，剪切带位置变化很大。随着εa的增加，各测线上γmax逐渐增加。

对于2#土样(图9)，当εa=0.019 9时，测线C0及两侧测线C1和C2上γmax的分布较均匀，且γmax较小。当εa=0.034 8时，与εa=0.019 9时相比，测线C0、C1和C2上γmax的分布较不均匀。此时，随着向孔洞表面的靠近，测线C1上γmax有下降趋势；在离孔洞较远位置，测线C1与土样左上角的应变不均匀区域相交，因受该区域的影响较大，导致离孔洞较远位置的γmax较大。随着向孔洞表面的靠近，测线C2上γmax呈先上升后下降趋势。当εa=0.062 1时，测线C0上γmax分布不均匀，在相同坐标情况下，测线C0上γmax比测线C1和C2上的都大。此时，随着向孔洞表面的靠近，测线C0上γmax先上升，再波动式下降，后上升。对于孔洞附近测点(s≥286.5像素)，随着向孔洞表面的靠近，测线C0上γmax有上升趋势，这可能是由于越靠近孔洞表面，γmax集中越严重，这说明剪切带C是从孔洞表面向外发展的。此时，对于孔洞附近测点(s≥278像素)，随着向孔洞表面的靠近，测线C1上γmax有下降趋势，这应与剪切带外弹性应变降低(卸荷)有关。此时，测线C2上γmax先上升再波动，后有下降趋势，在测线C2上s=109.5、168.5和252像素处γmax出现了高峰，这应与这些测点附近出现的剪切带分叉现象有关。此时，对于孔洞附近测点(s≥320.2像素)，随着向孔洞表面的靠近，测线C2上γmax有下降趋势，其原因与测线C1上的类似。随着εa的增加，各测线上大部分测点的γmax逐渐增加。对于测线C2，当εa=0.094 4时，与εa=0.086 9时相比，当s≤50.5像素和s≥278像素时，这些测点的γmax发生下降，这可能与带外弹性应变降低较大有关。

对于8#土样(图10)，当εa=0.023 0时，测线D0及两侧测线D1和D2上γmax的分布较均匀，且γmax较小。当εa=0.039 4时，测线D0上γmax的分布仍较均匀，而对于测线D1和D2，随着向孔洞表面的靠近，γmax有增大的趋势。当εa=0.039 4时，随着向孔洞表面的靠近，测线D0上γmax先有上升趋势后下降。此时，对于孔洞附近测点(s≥306.5像素)，随着向孔洞表面的靠近，测线D1上γmax有下降趋势，在s=306.5像素附近，测线D1上γmax较大，其两边γmax都较小，这与该区域附近出现的应变不均匀区域有关。此时，对于孔洞附近测点(s≥140.8像素)，随着向孔洞表面的靠近，测线D2上γmax有下降趋势，在s=140.8像素附近，测线D2上γmax较大，其两边γmax都较小，这与该区域附近出现的应变不均匀区域有关。当εa=0.069 0时，测线D0上γmax分布不均匀，测线D0的γmax比测线D1和D2上的大。此时，随着向孔洞表面的靠近，测线D0上γmax先上升至基本不变，再下降，后上升。当εa=0.069 0时，测线D0上中部区域的γmax较大，高达0.177 9，这说明剪切带D启动于测线D0中部某一位置，逐渐向外发展。此时，对于孔洞附近测点(s≥314.8像素)，随着向孔洞表面的靠近，测线D0上γmax有上升趋势，这与孔洞表面一定程度的γmax集中有关。当εa=0.069 0时，剪切带D与当εa=0.039 4时出现的应变不均匀区域相比，剪切带较陡。当εa=0.069 0时，对于孔洞附近测点(s≥306.5像素)，随着向孔洞表面的靠近，测线D1上γmax有下降趋势，这应与剪切带外弹性应变降低(卸荷)有关。此时，对于孔洞附近测点(s≥331.3像素)，随着向孔洞表面的靠近，测线D2上γmax有上升趋势，这应与孔洞表面附近出现的应变不均匀区域有关。

表2给出了4个土样不同εa时各条测线上γmax的平均值。可以发现，对于56#土样，测线A0上γmax远大于带外测线A1和A2，测线A0上γmax的均值是带外的2.15～10.78倍；当εa=0.024 5时，其倍数最大；随着εa的增加，测线A0上γmax的均值先下降再增加；测线A1上γmax有类似的演变规律，而测线A2上γmax的均值一直增加，这应与孔洞右帮偏上发展出的剪切带有关。对于17#土样，测线B0上γmax的均值是带外的0.81～9.02倍；εa越大，其倍数越大；在测线B0上γmax快速增加的同时，两侧测线B1、B2上γmax也在变化，但变化不大。2#土样和8#土样表现出与17#土样相类似的规律，不再赘述。

表2 土样不同εa时不同测线上γmax的平均值Table 2 Mean of γmax at different monitored lines for different εa of clay specimens

下面，对孔洞表面附近和离孔洞较远处测线上γmax的演变规律进行综合分析。

首先，对孔洞表面附近测线上γmax的演变规律进行分析。对于剪切带内而言，当εa较高时，土样测线上γmax随着向孔洞表面的靠近而增加，这应与孔洞表面附近的应变集中现象有关。例如，当εa≥0.076 7，且s≥281.7像素时，17#土样的测线B0，当加载速率较低时，土样中的一些原生缺陷或裂隙能够得到发展，而当加载速率较高时，这些内部缺陷来不及发展。对于剪切带外而言，大多数测线上γmax随着向孔洞表面的靠近而逐渐下降，这应与剪切带内损伤导致带外弹性应变降低(卸荷)有关。离孔洞表面越近，带外卸荷程度越大。

然后，对离孔洞较远处测线上γmax的演变规律进行分析。对于剪切带内而言，除了17#土样，当εa较高时，其他土样测线上γmax随着向孔洞表面的靠近而增加，这与越靠近孔洞γmax的集中程度越大有关。对于17#土样中的剪切带B，随着向孔洞表面的靠近，测线B0上γmax先上下波动，再下降，这应与剪切带B由土样右上角向孔洞表面发展有关。对于剪切带外而言，测线上γmax随着向孔洞表面的靠近，变化规律较为复杂。例如，随着向孔洞表面的靠近，当εa≥0.048 4，且s≤48.29像素时，17#土样的测线B2上γmax有下降的趋势，当εa≥0.034 8，且s≤109.5像素时，2#土样的测线C2上γmax有上升的趋势，当εa≥0.039 4，且s≤140.8像素时，8#土样的测线D2上γmax有上升的趋势。

3 结论

1)当加载速率较低，且纵向应变达到一定值时，在含孔洞土样的孔洞顶部和底部发展出的高角度应变局部化带是由拉破坏导致的，而当加载速率较高时，未出现上述现象。

2)含孔洞土样剪切带内测线上最大剪切应变的均值往往大于带外测线，最大可达10倍，通常，纵向应变越高，剪切带内测线上最大剪切应变的增速越大于带外测线。

3)当纵向应变较高时，在孔洞表面附近，随着向孔洞表面的靠近，大多数剪切带内测线上最大剪切应变逐渐增加，而大多数带外测线上最大剪切应变逐渐下降，这与带内损伤导致带外弹性应变降低有关。当纵向应变较高时，在离孔洞表面较远处，随着向孔洞表面的靠近，大多数剪切带内测线上最大剪切应变逐渐增加，而带外测线上最大剪切应变变化复杂。