考虑管土分离的基坑开挖引起邻近地下管线位移分析

何小龙，杨天鸿，周云伟，梁禄钜，徐长节,3

(1.杭州市钱江新城建设开发有限公司，杭州 310058；2.浙江大学 滨海和城市岩土工程研究中心，杭州 310058;3.华东交通大学 土木建筑学院;江西省岩土工程基础设施安全与控制重点实验室，南昌 330013)

近年来，随着中国城市立体化建设逐渐由地面及上部建设向地下延伸，城市地下工程规模越来越大，基坑越来越深。各大城市市政工程尤其是地铁工程的大量上马，使得繁华城区开挖深基坑变得越来越普遍，这将不可避免地出现地下工程深基坑邻近既有地下管线开挖的情况。

深基坑的开挖往往会改变土体的初始应力状态，使土体产生变形，进而造成基坑边邻近管线的破坏。对于此类邻近地下工程施工对既有管线影响的工程问题，已有不少学者开展了相应研究。Tan等[1]对两例邻近地下既有管线深基坑开挖工程进行了详细的案例分析，并通过大量现场实测数据，提出了邻近深基坑开挖情况下既有地下管线变形计算的经验公式；Zhang等[2]通过有限元数值模拟方法，对深基坑开挖对邻近管线的内力与变形特性进行了研究；Wham等[3]针对下卧盾构隧道施工对上覆既有铸铁管线接头的影响，开展了数值模拟研究；通过离心模型试验方法，Oliveira等[4]和Shi等[5]分别研究了土体侧向移动及下方盾构施工对既有地下管线三维变形特性的影响。韩煊等[6]基于大量地下管线实测变形数据，提出了连续管线变形和内力预测的刚度修正法。这一系列研究结果进一步说明了地下工程施工对邻近管线的危害，但所得到的多为经验性结论，缺乏对附加荷载作用下地下管线内力与变形方面的定量评估。

1 计算模型与基本假定

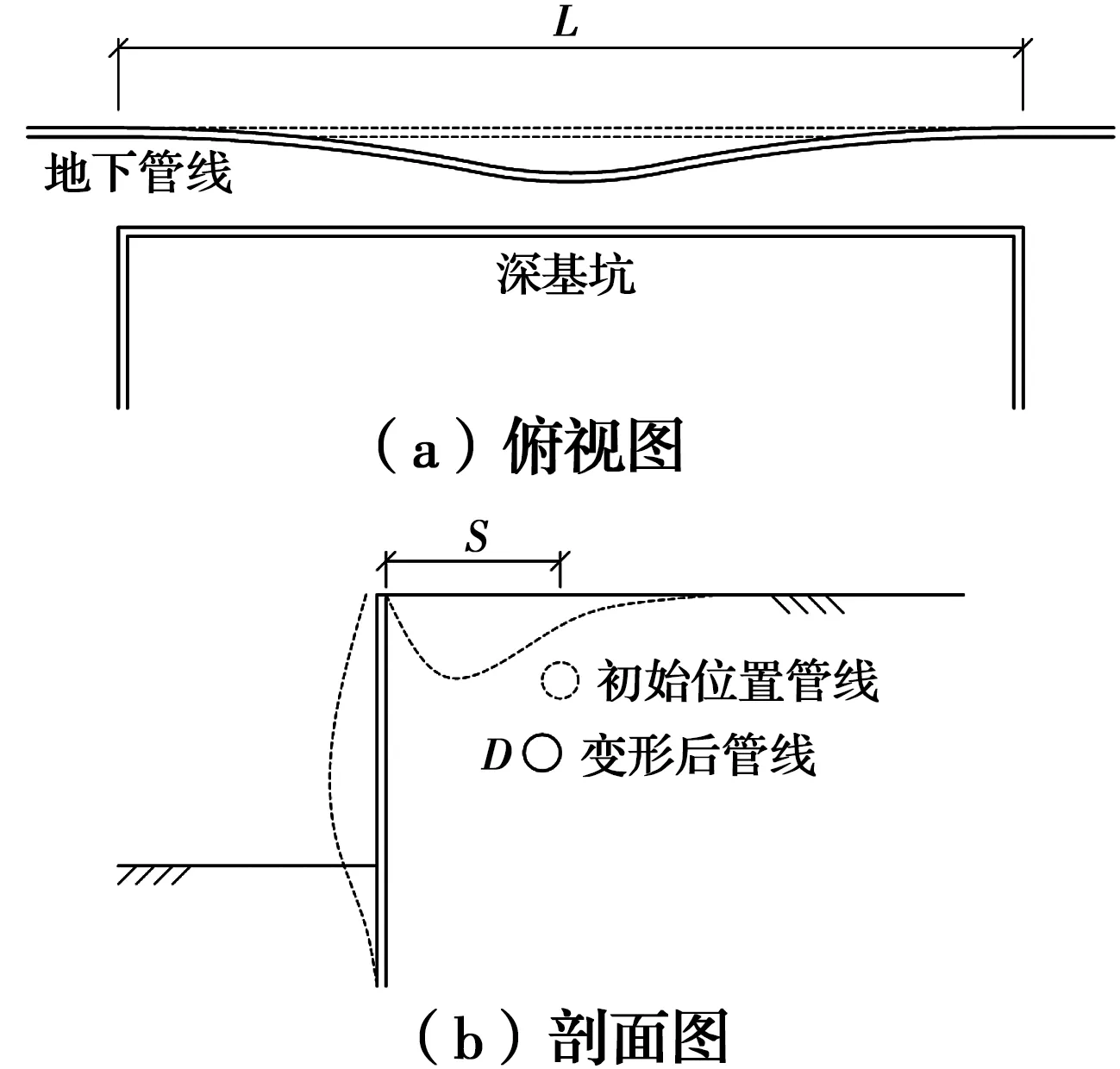
图1 邻近深基坑开挖地下管线Fig.1 Buried pipeline adjacent to a foundation

1)地下管线为一无限长的Euler-Bernoulli梁；

2)地基土为由剪切层和弹簧组成的Pasternak弹性地基[17]，地基土间的剪应力由剪切层承担；

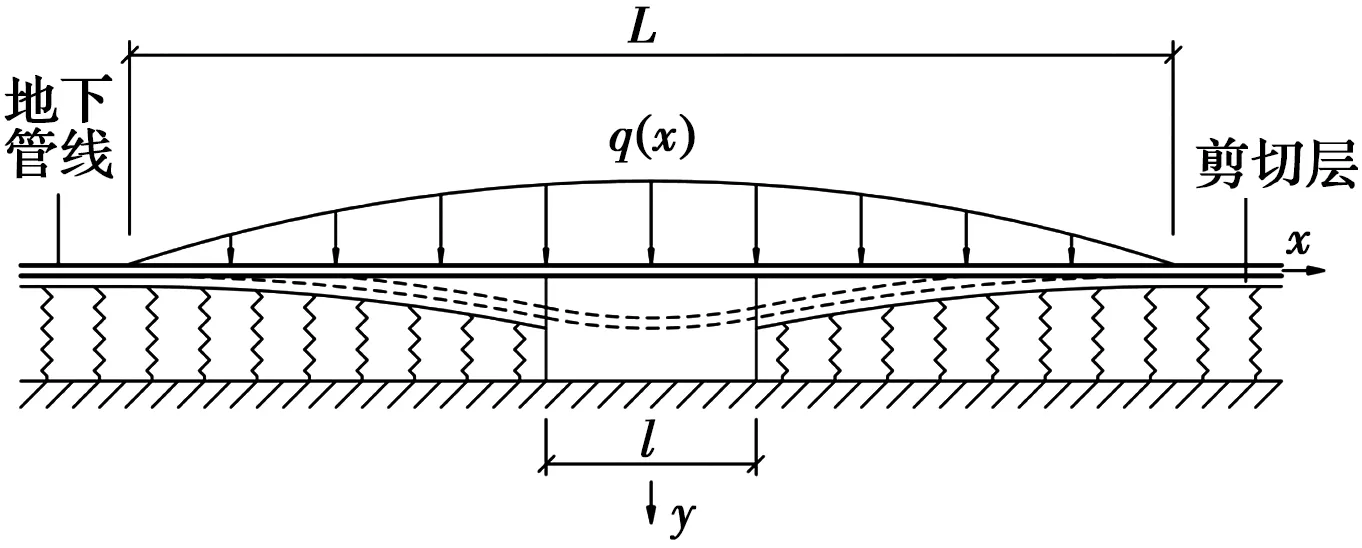
图2 计算模型

2 解析公式推导

2.1 管土分离部分

(1)

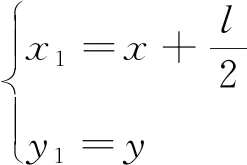
(2)

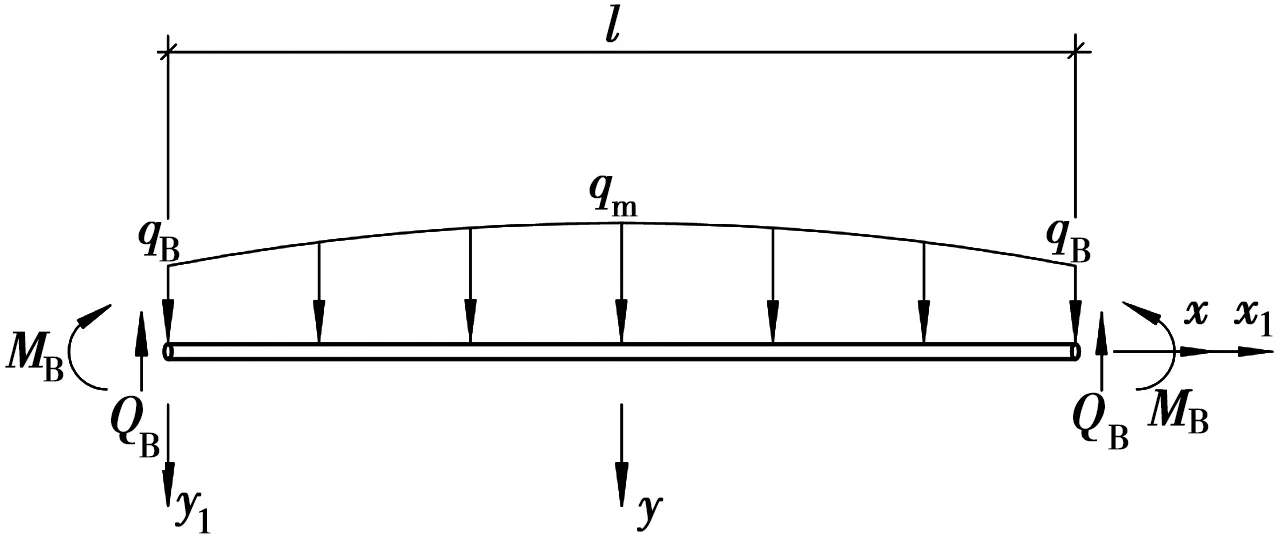
图3 管土分离部分管线受力分析Fig.3 Mechanical analysis of a pipeline in the separation

在新的坐标系下，根据Euler-Bernoulli梁理论，地基梁上任一点的弯矩可表示为

(3)

式中：MB和QB分别为管线端点上的弯矩与剪力。

将式(1)和式(2)代入式(3)并积分，可得

(4)

式中：C1和C2为未知积分常数。该段地基梁的边界条件为

(5)

式中：yB为端点处地基梁的位移。将边界条件式(5)代入式(4)，解得

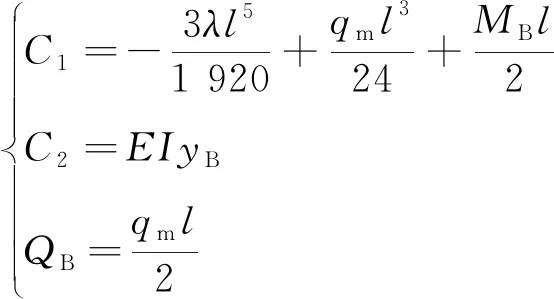
(6)

2.2 管土未分离部分

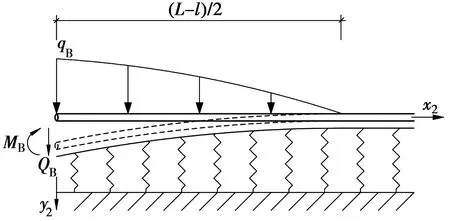
图4 管土未分离部分管线受力分析Fig.4 Mechanical analysis of a pipeline in

为方便分析，建立新的坐标系(x2,y2)。

(7)

根据Pasternak弹性地基梁理论，在外荷载q(x2)作用下，管线需满足控制方程

(8)

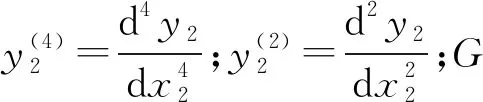
地基竖向基床系数k可通过工程地质勘察报告获得。当无相关参考资料时，地基竖向基床系数k和剪切层竖向剪切刚度G可由式(9)进行计算[15,18]。

(9)

式中：Es和vs分别为地基土体的弹性模量和泊松比。t为土体剪切层厚度，其大小与土体参数有关。根据文献[19]建议，取t=2.5D进行计算。令

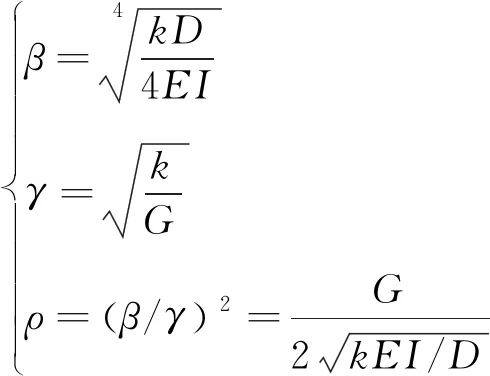
(10)

则常微分方程式(8)所对应的齐次方程可写为

(11)

对于目前工程中常用的PVC管线、铸铁管线和混凝土管线，ρ的计算结果一般均小于1。此时，该四阶齐次常微分方程的通解为

y2=(A1e-φ1x2+A2eφ1x2)cosφ2x2+

(A3e-φ1x2+A4eφ1x2)sinφ2x2

(12)

式中：

(13)

A1、A2、A3、A4为4个积分常数，由于无穷远处管线位移为0，故必有A2=A4=0。其他两个积分常数可通过边界条件求解。根据图4中的受力分析，作用在该段地基梁上的外力包括：梁端剪力QB、梁端弯矩MB以及非均布荷载q(x2)。故可分3种情况分别进行求解，最后，将所得结果叠加，从而得到该段地基梁位移的最终解。

(14)

将式(12)代入式(14)，解得

(15)

第2种情况，即梁端作用集中弯矩MB，这种情况下地基梁的边界条件为

(16)

将式(12)代入式(16)，解得

(17)

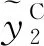
(18)

当x2∈[0,(L-l)/2]时，因为q(x2)为二阶多项式，故假设

(19)

将式(19)代入式(8)，解得

(20)

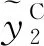
(21)

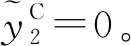
(22)

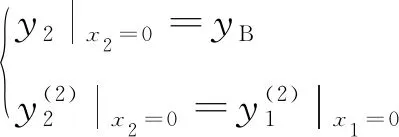
(23)

可解得

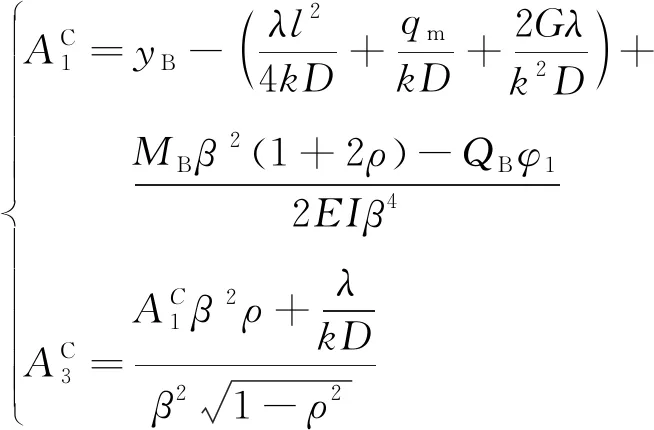
(24)

进一步根据变形协调条件

(25)

解得

(26)

(27)

3 结果验证

3.1 有限元结果对比

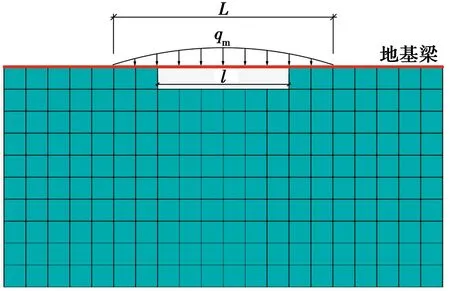
图5 数值分析模型Fig.5 Analytical model of numerical

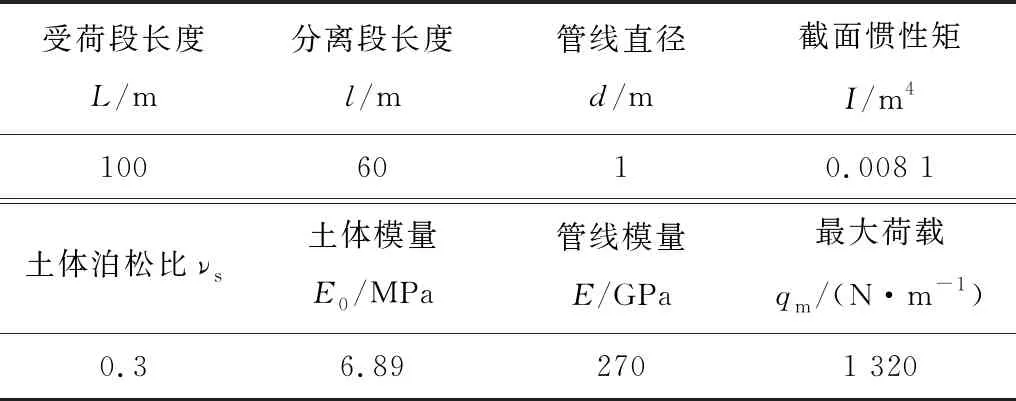
表1 数值模拟参数Table 1 Parameters of numerical simulation

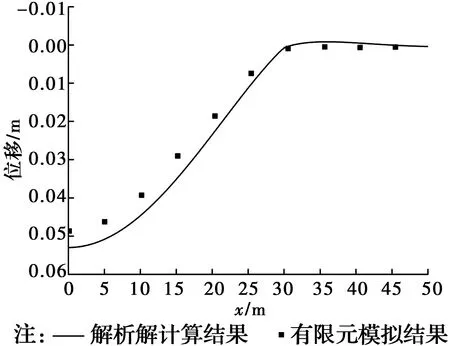
图6 解析解计算结果与数值模拟结果对比Fig.6 Comparison between analytical and

3.2 实测数据对比

为进一步验证理论模型在基坑开挖引起邻近管线响应分析方面的适用性，引用一组基坑工程实例进行分析。杭州市钱江新城沿江大道综合管廊基坑呈长条形状，长度为216.0 m，深度为16.0 m，宽度为10.7 m，基坑围护结构采用地下连续墙加4道内支撑的支护形式，地下连续墙为800 mm的C30混凝土，第1、3道为钢筋混凝土支撑，第2、4道为钢支撑。基坑周边有需要保护的大直径污水管线，坑边与污水管线水平距离相距4.0 m，污水管线由2根型号D2400的预应力钢筒混凝土管组成，污水管管径为2.4 m埋深约10 m左右。典型的基坑围护剖面如图7所示。现场实测基坑围护结构中点位置管线的最大荷载qm=14.9 kN/m，其他计算参数如表2所示。

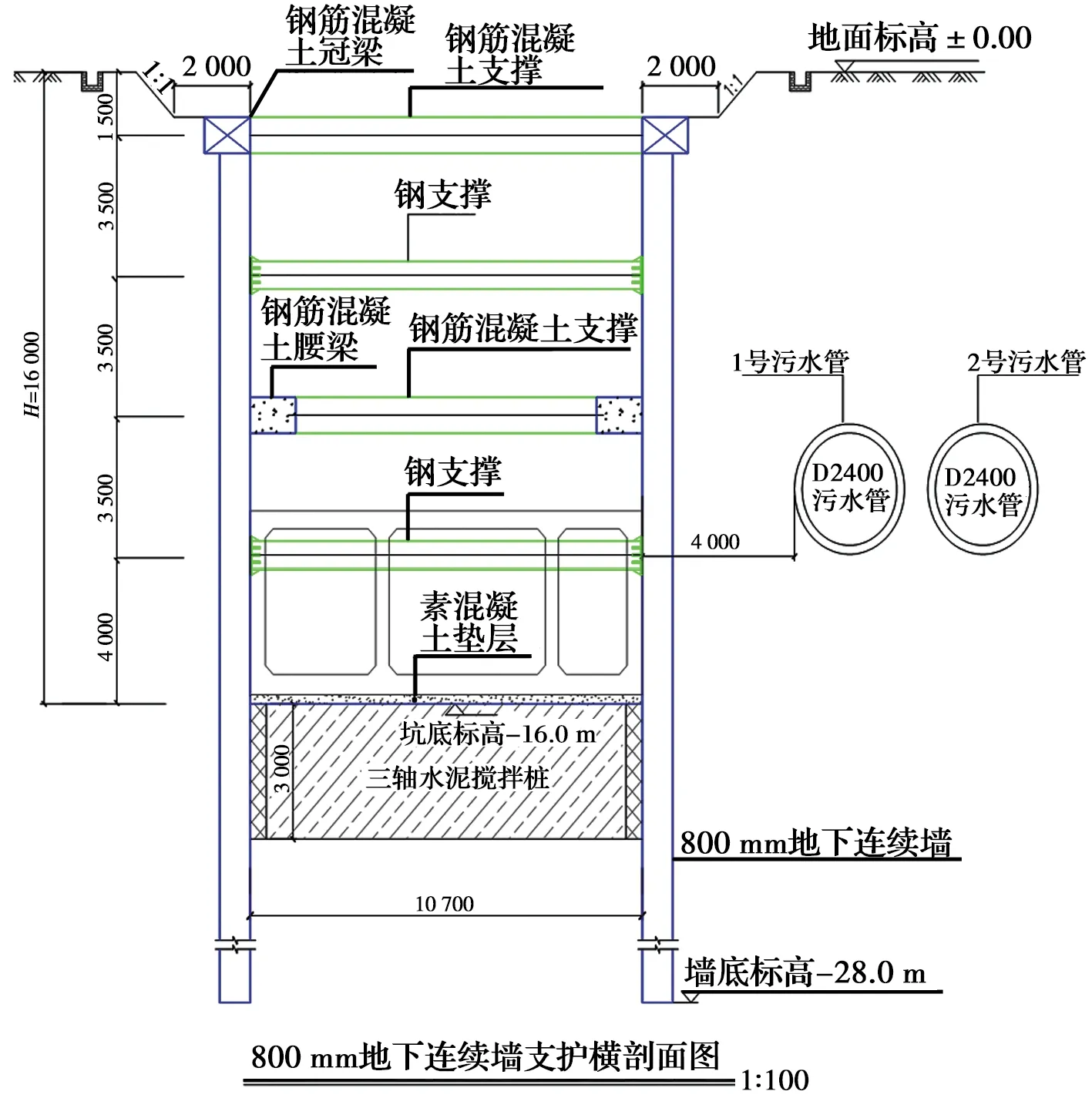
图7 基坑围护结构剖面图Fig.7 Profile map of foundation pit enclosure

表2 计算参数Table 2 Calculation Parameters

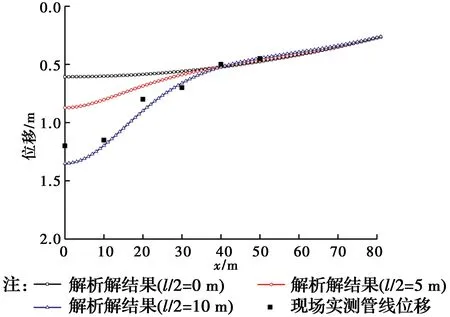
图8 解析解与现场实测结果对比Fig.8 Comparison between analytical results

4 参数分析

为进一步分析本文计算模型中各计算参数对邻近基坑开挖管线响应的影响，现以表1中的计算参数为基础，进行相应的参数敏感性分析。

4.1 土体及管线刚度影响

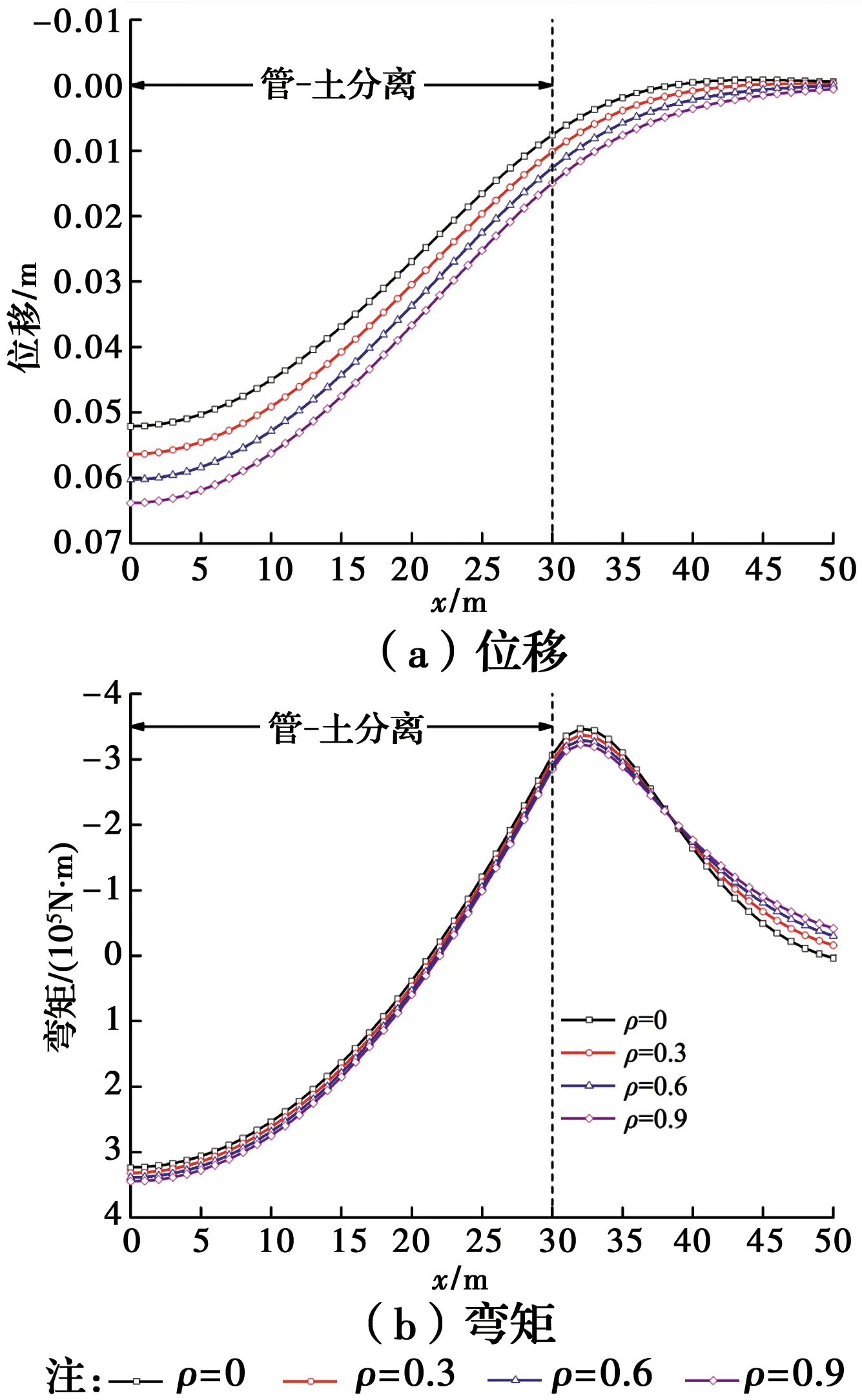
图9 不同土体剪切刚度情况下管线响应Fig.9 Responses of pipeline under different shear

4.2 管线最大荷载影响

当qm较难通过现场实测获得时，根据Pasternak弹性地基模型，可通过基坑开挖情况下管线位置处土体自由位移场进行计算得到。

(28)

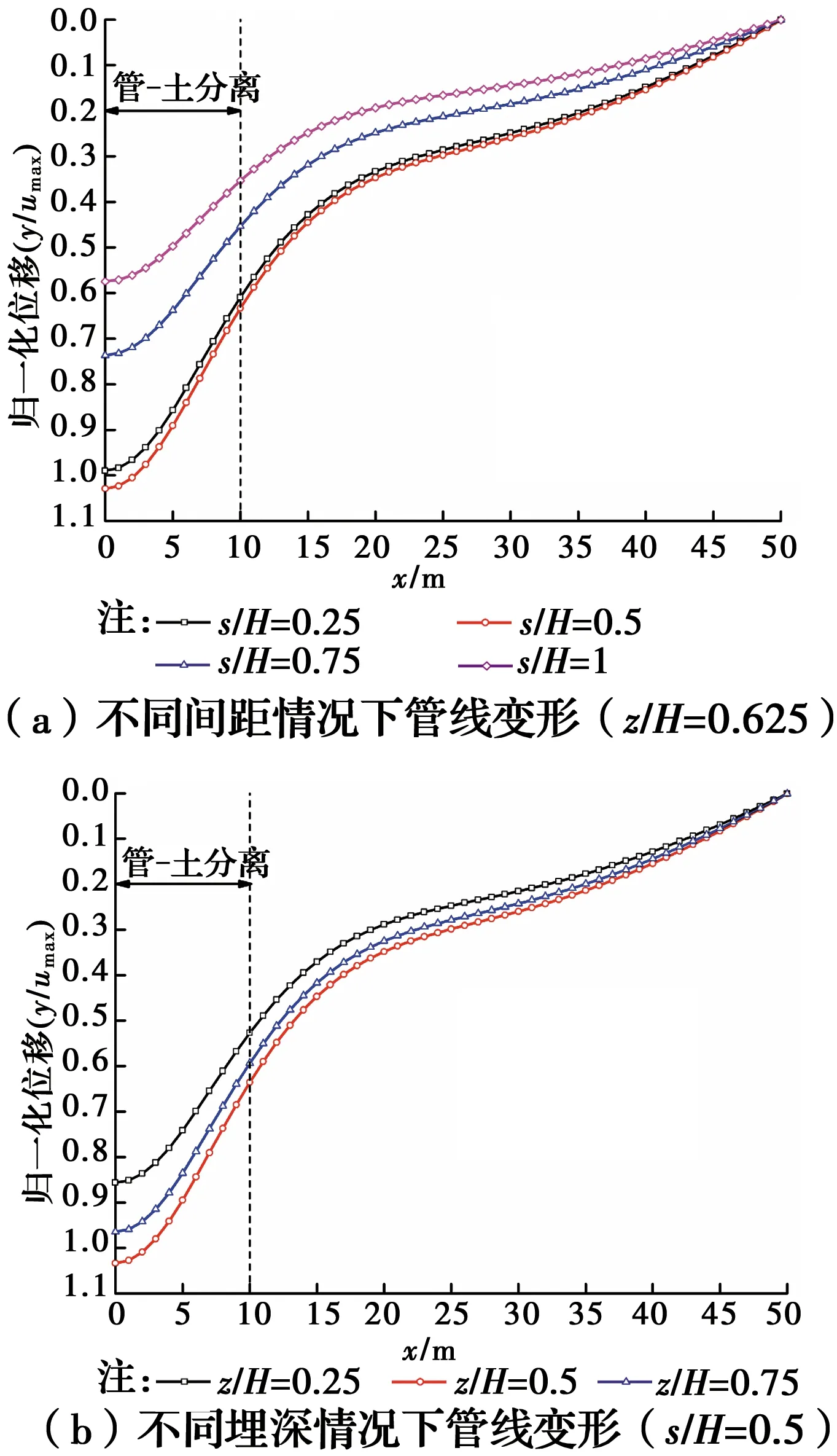
图10 基坑开挖对既有管线变形影响Fig.10 Influences of foundation pit excavation

由图10可知，在其他因素相同的情况下，管线及基坑间距对管线变形的影响大于管线埋深对管线变形的影响。而由于基坑开挖周边土体三维位移场的影响，邻近基坑既有管线的变形随着其埋深和与基坑围护结构间距的增加，均呈先增大后减小的趋势。在z/H=0.5和s/H=0.5的位置附近，存在一管线变形的最大区域。因此，在实际工程中，对于位于这一位置附近的既有管线应进行重点保护。

5 结论

2)既有地下管线最大位移随着其埋深和距基坑围护结构距离的增大，呈先增大后减小的趋势，且管线及基坑间距对管线变形的影响较大。

3)土体剪切刚度对地下管线变形计算具有显著影响。计算过程中若不考虑土体间的剪切效应，将使得计算结果偏于不安全。同时，管线刚度越小，土体间剪切效应对管线变形计算的影响将越大。