点差法在圆锥曲线中的应用探究

王跃梅

(江苏省射阳县高级中学，江苏 盐城 224300)

点差法在圆锥曲线中的应用探究

王跃梅

(江苏省射阳县高级中学，江苏 盐城 224300)

点差法，顾名思义，设点、作差，它是利用直线与圆锥曲线的交点，再将交点坐标代回原曲线方程，并将两式相减，即可得到一个关于弦的中点及斜率的方程，利用该方程求解一些轨迹问题.在高中数学中，点差法主要用于圆锥曲线中如下的三类计算：1)中点弦轨迹求解问题；2)圆锥曲线轨迹求解问题；3)圆锥曲线定值定点问题.在本文中，我们将结合实际习题，对点差法的应用进行讨论.

高中数学；点差法；数学思想

一、点差法在中点弦方程求解中的应用

综上可知，所求的直线方程为x+2y-4=0.

点评针对中点弦方程的求解类问题，点差法是最有效的求解方式之一.本题属于基础类的中点弦方程求解问题，因为我们已经指明了点M位于椭圆内部，即可直接进行求解，无需再进行验证.对于例题中所示的题型，只要给出曲线方程及某个定点的坐标，利用点差法即可实现求解.若将本题进行变化，将条件“椭圆”变成“双曲线”，则需要重新进行考虑，需要对点的位置进行讨论，满足条件的直线可能不止一条，也可能不存在.在实际求解过程中，很多学生会忽视，从而功亏一篑.

二、点差法在圆锥曲线方程求解中的应用

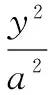
点评从上述解题过程可以看出，点差法贯彻了设而不求的思想，设出直线与椭圆的交点坐标，却并没有直接求解，而是利用和与差的关系，将解题所需的计算尽量简化，提高解题准确率.在点差法求解圆曲线方程的过程中，依然按照固定模式，设点、作差，导出斜率.在求解椭圆长短边的平方值过程中，还是贯彻简化计算的理念，围绕弦直线的斜率、中点坐标这两个关键，得到相应的关系式，利用关系式简化求解，体现出了点差法求解的精髓.

三、点差法在圆锥曲线定值定点问题中的应用

例3 在抛物线y2=2px(p>0)上有两点A、B，这两点满足关系OA⊥OB，其中O为坐标原点，求证：(1)A、B两点的横纵坐标之积都是一定值；(2)直线AB过定点.

点评本题利用点差法求解圆曲线中定值定点类问题，结合直线的斜率表达式，有效地简化了计算过程，巧妙地避免了方程组求解的繁琐步骤.由该例可以清晰地看出，点差法在求证定点定值类问题中，通过设点、作差两步，即可实现清晰有效的求证，值得注意的就是将作差所得条件向欲证信息的靠拢上，寻求合适的简化方法，得到准确的表达形式.

总之，点差法在圆锥曲线中的应用十分广泛，上述三类应用只是较为典型的案例而并非全部.点差法在弦中点证明、判断两点关于某一弦对称及弦的垂直平分线等众多方面均有着广泛的应用.在点差法中，这种设而不求的数学理念值得我们一线教师进行推广发扬.

[1]陈国辉.用点差法解圆锥曲线的弦中点问题[J].数理化解题研究，2016(01).

[2]杨亢尔.“点差法”在中点弦问题中的“意外”[J].数理化解题研究，2012(03).

G632

A

1008-0333(2017)22-0027-03

王跃梅(1976.05- )女，江苏徐州人，本科学历，中学一级教师，主要从事高中数学教学与研究.

责任编辑：杨惠民]