斜齿轮副结构参数灵敏度分析

,

(1.福州职业技术学院 交通工程系，福建 福州 350108； 2.国网福建省电力有限公司 信号通信分公司，福建 福州 350003)

斜齿轮副结构参数灵敏度分析

林梅彬1,郑蔚涛2

(1.福州职业技术学院 交通工程系，福建 福州 350108； 2.国网福建省电力有限公司 信号通信分公司，福建 福州 350003)

以机械传动系统中的斜齿轮啮合为研究对象，在考虑时变刚度、齿侧间隙和啮合误差的情况下，建立了十自由度斜齿轮非线性振动数学模型。以斜齿轮结构参数作为灵敏度分析参数，采用数值分析方法分别研究了斜齿轮系统振动加速度均方根值对齿轮质量、支撑刚度和支撑阻尼的灵敏度。结果表明：主、被动轮横向(y向)振动对各参数敏感度较低，横向振动(x向)与被动轮扭转振动对质量参数、刚度参数、阻尼参数较为敏感，被动轮扭转振动受到阻尼的影响很大，灵敏度在扭转振动固有频率处变化较大。

非线性;齿轮系统;刚度;阻尼;灵敏度

齿轮系统存在众多非线性因素，其中最重要的是时变啮合刚度和齿侧间隙。这些非线性因素不仅对齿轮系统振动特性产生很大影响，同时也是齿轮系统振动噪声的主要原因之一[1]。

齿轮非线性研究基本都是以非线性振动理论为基础，Hamed等[2]对含有动态传递误差的单自由度齿轮系统进行了研究，发现在不同条件下系统的稳定性与不稳定性产生明显的跳跃现象。魏静等[3]以斜齿轮为研究对象，建立了一种改进的齿轮副弯-扭-轴-摆耦合分析模型，研究了斜齿轮各非线性因素对振动动态特性的影响。其结果表明，随着系统激励频率不断增加，系统的振动周期性发生不同的变化，在固有频率附近，系统会出现较大振动响应。Lassad等[4]建立了十二自由度的齿轮模型，结合时变啮合刚度分析了齿轮非线性行为，研究发现当啮合齿轮轮齿位移大于齿侧间隙时，可以清晰地观测到缺齿接触现象。基于齿轮非线性系统模型的灵敏度研究随着非线性动力学研究的发展而发展起来。虽然齿轮系统在可靠性应用方面取得了一定的成果[5-10],但是在齿轮振动响应对结构参数灵敏度方面的研究还较少。文献[11]针对斜齿轮副动态特性的灵敏度问题，在考虑齿轮啮合耦合以及轴承因素的影响下推导了斜齿轮系统的灵敏度计算公式，主要求解的是结构参数对固有频率的影响，并未涉及系统响应对结构参数的灵敏度。

本文通过建立十自由度斜齿轮非线性振动数学模型，以齿轮质量、支撑刚度和支撑阻尼作为灵敏度分析参数，将振动响应均方根值的灵敏度作为评价指标，具体分析系统响应对结构参数的灵敏度，为齿轮系统的优化设计提供思路。

1 多自由度齿轮非线性系统的建立

1.1 数学模型的建立

图1为建立的斜齿轮副弯-扭-轴-摆耦合的非线性振动动力学模型[12]，为对模型进行简化，齿轮传动轴的扭转变形和齿面摩擦没有考虑在内。

图1 斜齿轮传动系统动力学模型Fig.1 Dynamic model of helical gear transmission system

该模型包含了横向振动(x和y)、轴向振动(z)、扭转振动(θz)、扭摆振动(θy)。用广义位移阵列可以表示为：

{δ}={x1,y1,z1,θ1y,θ1z,x2,y2,z2,θ2y,θ2z}T

该系统分析模型下推导得：

式(1)～(3)中的啮合力主要由以下式子表示：

式(11)～(13)中

式(14)～(16)中，ex、ey、ez分别为x、y、z三方向的啮合误差。kmx、kmy、kmz分别为啮合刚度在各方向上的分量。

设齿轮副侧隙为2b，则间隙非线性函数f表达式为：

1.2 量纲一化数学模型

将式子(1)～(10)进行无量钢化，得到的无量纲化数学模型如下：

量纲化后的间隙非线性函数由式(28)表示：

2 灵敏度分析方法

对于灵敏度微分方程较易推导的系统或模型，直接求导法是一种简单快速的灵敏度分析方法。时变系统可以用微分-代数方程进行描述。该种方法可以给出导数的解析表达式，求导过程由计算机来辅助完成。

为了研究齿轮系统结构参数灵敏度，本文采用振动均方根值对结构参数的灵敏度数值大小来识别敏感参数，推导出响应的均方根值对参数j的灵敏度公式。假设x方向的响应均方根值为：

将式(29)对j求导得

从式(30)可知，求取振动响应均方根值对参数j的灵敏度，需要知道响应的时域曲线以及振动响应对参数j的灵敏度时域曲线。对公式(18)～(27)进行求解，可以求出无量纲模型的时域响应p1～p10，而对应每一个动态响应，都可以求出每个响应对应于一定时域区间的均方根值。对公式(18)～(27)进行求导(对应于不同参数，求导方程不同)，即可以求出响应p1～p10的灵敏度时域曲线。通过以上方法可求出系统响应对结构参数的灵敏度。

3 齿轮系统的参数灵敏度分析

3.1 系统响应对质量参数的灵敏度

齿轮系统的参数如表1所示，采用四阶变步长Runge-Kutta法对模型进行数值求解。无量纲频率f取值区间为[0.01 0.73]，无量纲时间τ取值区间为[0，30000]，得到齿轮系统振动响应均方根值对质量参数的灵敏度如图2所示。

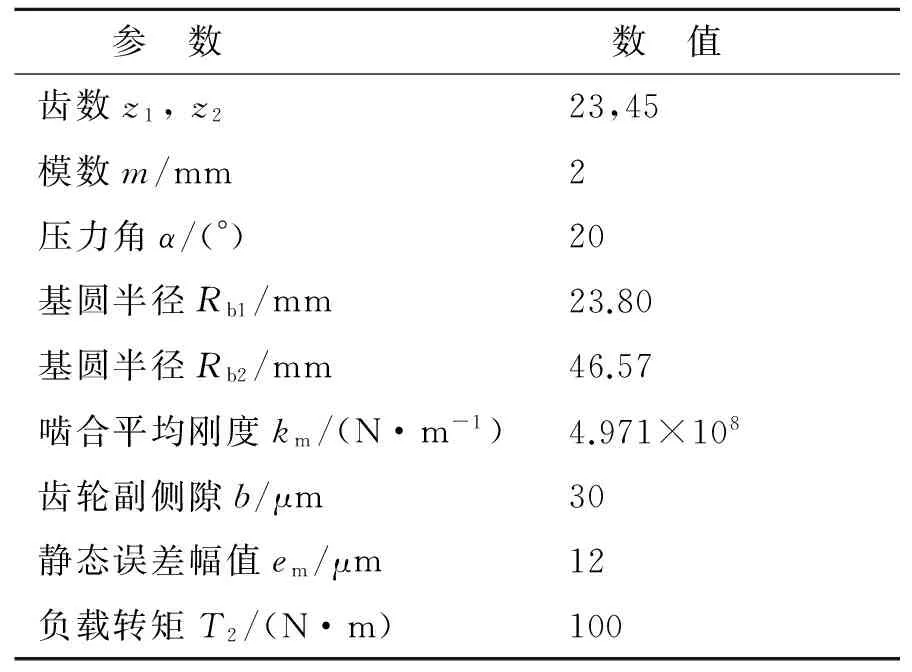
表1 齿轮系统参数Tab.1 Parameter of gear system

图2列举了响应对质量参数的灵敏度(对于不敏感的响应灵敏度未列图中)。由图2(a)可知，对质量m1敏感的系统响应为主动轮横向振动(x1)和被动轮横向振动(x2)。在频率增加的过程中，主动轮横向振动对主动轮质量m1最敏感，灵敏度方向始终为负，且灵敏度的大小在-0.003 kg-1至-0.001 kg-1之间波动。增加主动轮的质量将会减小主动轮横向振动。相比其他动态响应，被动轮横向振动对质量m1也十分敏感，且灵敏度方向始终保持负数。需要注意的是，在频率f=0.65(通过模态分析得到此频率在二阶扭转振动固有频率附近)，主、被动轮轴向振动对质量m1灵敏度数值达到最大值，而在其他频率下不敏感。

由图2(b)可知，对质量m2敏感的响应为主动轮横向振动(x1)、主动轮扭转振动和被动轮扭转振动。除在f=0.63，增加被动轮质量，有利于减小主、被动轮扭转振动。随着频率的增加，主、被动轮扭转振动灵敏度变化不大。在低频段，主动轮横向振动灵敏度波动较大。在高频段，主动轮横向振动敏感度降低。从灵敏度数量级来看，主动轮质量对系统响应的影响比被动轮质量对系统响应的影响大。

(a)主动轮质量m1的灵敏度

(b)被动轮质量m2的灵敏度图2 系统响应对质量参数的灵敏度Fig.2 System response sensitivity to mass parameter

3.2 系统响应对支撑刚度参数的灵敏度

系统响应对支撑刚度的灵敏度数量级如表2所示(对于不敏感的响应灵敏度未列图中)。由表2可知，系统响应对y向刚度参数的灵敏度数量级最大，达到10-5。因此y向刚度是对系统响应影响最大的刚度参数，仿真分析得到系统响应均方根值对y向刚度参数的灵敏度如图3所示。

表2系统响应对支撑刚度灵敏度数量级
Tab.2Magntiudeofsystemresponsesensitivitytopedestalstiffness

参 数灵敏度数量级k1x10-10k1y10-5k1z10-10k2x10-13～10-12k2y10-5k2z10-12～10-11

(a)刚度k1y的灵敏度

(b)刚度k2y的灵敏度图3 系统响应对刚度参数的灵敏度Fig.3 System response sensitivity to stiffness parameter

由图3(a)可知，在低频段，随着频率增加，系统响应对刚度k1y的灵敏度增大，但是在频率f∈[0.42 0.51]的区间内以及f=0.52(通过模态分析得到此频率在一阶扭转振动固有频率附近)，系统响应灵敏度方向均发生了变化。在f=0.67，除主动轮横向振动(x1)灵敏度继续保持增大外，其他系统响应灵敏度都变化为极小值。主动轮扭转振动的灵敏度绝对值变化最小。综合来看，对刚度k1y敏感度从高到低依次为主、被动轮轴向振动、主动轮横向振动(x1)、被动轮扭转振动、主动轮扭转振动。

由图3(b)可知，在低频段，随着频率的增加，系统响应对刚度k2y的灵敏度增大。在频率增加的过程中，同样也出现了灵敏度方向变化的区域。

与刚度k1y灵敏度不同的是，被动轮的横向振动(x2)变为敏感因素。综合来看，对刚度k2y敏感度从高到低依次为主、被动轮轴向振动、被动轮横向振动(x2)、被动轮扭转振动、主动轮横向振动(x1)、主动轮扭转振动。

3.3 系统响应对阻尼参数的灵敏度

系统响应对支撑刚度的灵敏度数量级如表3所示。由表3可知，系统响应对c2y参数的灵敏度数量级最大，其灵敏度最大值数量级达到10-4。因此，y向阻尼参数是对系统响应影响最大的阻尼参数，仿真分析得到系统响应均方根值对c2y的灵敏度如图4(对于不敏感的响应灵敏度未列于图中)所示。

表3系统响应对支撑阻尼灵敏度数量级
Tab.3Magntiudeofsystemresponsesensitivitytopedestaldamping

参 数灵敏度数量级c1x10-7～10-6c1y10-6～10-5c1z10-6c2x10-9c2y10-5～10-4c2z10-9

由图4可知，被动轮扭转振动对阻尼c2y非常敏感，除在f=0.67，被动轮扭转振动灵敏度达到极小值以外，在其他频率下，其灵敏度都为最大。增大c2y可以大大降低被动轮扭转振动。综合来看，对阻尼c2y敏感度从高到低依次为被动轮扭转振动、主、被动轮轴向振动、被动轮横向振动(x2)、主动轮横向振动(x1)、主动轮扭转振动。

图4 响应对阻尼c2y的灵敏度Fig.4 System response sensitivity to damping c2y

4 结论

1)系统的横向振动响应(x向)与扭转振动受到系统的质量参数、刚度参数与阻尼参数的影响较大。

2)相比其他系统响应来说，y向振动对所有参数的敏感度都较低。

3)增大被动轮支撑阻尼参数(y向)，可以大大降低被动轮的扭转振动。

4)齿轮系统的振动灵敏度在扭转振动固有频率处附近的变化较大，可以为齿轮系统优化设计提供方向，为设计出更好的齿轮系统提供指导性建议。

[1] 张策,机械动力学[M].北京：高等教育出版社,2008.

[2] Hamed M，Hassan S.Analysis of nonlinear oscillations in spur gear pairs with approximated modeling of backlash nonlinearity[J].Mechanism and Machine Theory,2012,51:14-31.

[3] 魏静,孙伟,秦大同,等.基于改进的弯-扭-轴-摆耦合模型的斜齿轮动态特性及非线性因素影响分析[J].机械工程学报，2011,47:1-9.

[4] Lassad W，Tahar F，Mohamed H.Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation，bearing flexibility and backlash[J].Mechanism and Machine Theory,2009,44(5):1058-1069.

[5] Arsham H.Perturbation analysis of general lP models: A unified approach to sensitivity,parametric tolerance,and more-for-less analysis[J].Mathematical and Computer Modelling,1990(12):1437-1446.

[6] Ramakrishnan C V,Francavilla A.Structural optimization using penalty functions[J].J Struct Mech,1974(3):403-422.

[7] Wang S Y,Sun Y,Gallagher R H.Sensitivity analysis in shape optimization of continuum structures[J].Comp and Struct,1985,20:855-867.

[8] 安宗文,辛玉.基于重要抽样法的风电齿轮箱齿轮可靠性灵敏度分析[J].兰州理工大学学报,2015,41(3):300-305.

[9] 刘中生,陈塑寰.齿轮传动系统扭振固有频率对设计参数的灵敏度[J].机械工程学报,1993,29(2):77-83.

[10] 周娜,张义民.圆锥齿轮可靠性分析的参数灵敏度[J].中国机械工程,2008,19(21):2617-2622.

[11] 魏兵,夏明安.齿轮系统减振设计的支承结构灵敏度分析[J].武汉交通科技大学学报,2000,24(3):313-315.

[12] 郭磊.斜齿轮多间隙非线性耦合系统动力学研究[D].大连:大连理工大学,2010.

(责任编辑：陈雯)

Analysisoftheparametersensitivityofhelicalgearpairs

Lin Meibin1,Zheng Weitao2

(1.Transportation Engineering Department,Fuzhou Polytechnic (Institute of Technology),Fuzhou 350108,China;2.Signal Communication Sub-company,National Grid Fujian Provincial Electric Power Co.,Ltd.,Fuzhou 350003,China)

A nonlinear vibration mathematical model of ten degrees of freedom of a helical gear system was established,in which time-varying meshing stiffness,backlash and meshing errors were considered.The structural parameters of the helical gear were employed as the parameters of sensitivity analysis to investigate the vibration acceleration square root value sensitivity of the helical gear system to gear mass,stiffness of bearing pedestal and damping via numerical analysis method.The results show that the horizontal vibration and driven gear tortional vibration are more sensitive to the parameters of the gear,mass,stiffness，while the tortional vibration of the driven gear is sensitive to the damping with the sensitivity varying considerably at the natural frequency of torsional vibration.

nonlinearity;gear system;stiffness;damping;sensitivity

TH113.1；TH132.41

A

1672-4348(2017)04-0328-05

10.3969/j.issn.1672-4348.2017.04.005

2017-04-05

福建省中青年教师教育科研项目(JAT171066)

林梅彬(1989-)，男，福建泉州人，助教，硕士，研究方向：汽车振动与噪声控制.