冲击荷载作用下钢框架的动态响应分析

，,2，

(1.福建工程学院 土木工程学院，福建 福州 350118;2福建省土木工程新技术与信息化重点实验室，福建 福州 350118)

冲击荷载作用下钢框架的动态响应分析

杨绵越1，付朝江1,2，陈洪均1

(1.福建工程学院 土木工程学院，福建 福州 350118;2福建省土木工程新技术与信息化重点实验室，福建 福州 350118)

在冲击荷载作用下，钢框架结构的动态响应是一个复杂的非线性过程。运用ANSYS/LS-DYNA建立了钢框架的三维模型，对冲击荷载作用下钢框架的动态响应和破坏形态进行研究。采取多点积分算法，有效避免沙漏问题，保证计算结果精确。以冲击块与钢框架的碰撞冲击为例，研究了冲击速度、冲击块质量、冲击位置等参数对钢框架在横向冲击作用下动力响应的影响，并分析冲击荷载下钢框架的破坏形态。结果表明：冲击块的质量、速度、冲击位置的增加都会不同程度地加剧钢框架的动态响应；在冲击作用下，高应变主要出现在被冲击柱子的冲击区域、柱脚处和梁柱节点处；冲击荷载下钢框架的破坏形态为整个框架发生侧移，受冲击柱在冲击处翼缘出现局部屈曲，受冲击区域的截面发生弯扭，未受冲击柱出现倾斜。

冲击荷载； 钢框架； 多点积分； 动态响应； 破坏形态

在钢结构的使用期间，其遭遇冲击、碰撞等多灾变交合破坏作用的事件频频在世界各地发生，其中损失和伤亡最大要属于美国“911”事件。并且由于钢结构的自重较轻、截面开展的特点，其一旦遭遇撞击或冲击等外界动力荷载的作用，结构或构件的损伤和破坏程度势必会高于一般的混凝土结构和组合结构。因而，开展对钢框架的抗冲击研究，对于理解整个结构在冲击荷载作用下的力学行为，考察钢框架的抗冲击性能，对钢框架的抗冲击设计具有一定的指导意义，对现实的工程具有一定的理论意义和现实意义。

国外学者对冲击荷载下单个构件的研究较多，对冲击荷载作用下钢框架的研究较少。G.M.Nagel[1]等人采用三角脉冲荷载对自由梁进行冲击响应分析，得到了冲击载荷作用下自由梁的动态变形机制； HengPiseth和HjiajMohammed[2]等人对两端固支梁进行了冲击试验，提出了固支梁在均布冲击荷载下的3种失效模式：非弹性大变形、拉伸破坏、支承处的剪切破坏。

在国内，朱斌[3]等人对水上埋置框架结构进行在撞击力作用下的动力特性研究；霍静思[4]等采用落锤冲击试验机对4个热轧H型钢梁进行了动态抗冲击力学性能试验研究；王蕊[5]等采用Abaqus有限元软件对热轧型钢(HW100 mm × 100 mm × 6 mm× 8 mm)受侧向冲击荷载作用下的力学性能进行了参数分析研究；张峰峰[6]通过ANSYS/LS-DYNA软件数值模拟对性连接钢框架和半刚性连接钢框架受冲击过程进行了数值仿真研究；宿专青[7]通过对通过有限元软件建立数个传统钢框架和新型梁翼缘削弱型钢框架有限元模型，研究其在撞击作用下的动力响应。

本文基于ANSYS/LS-DYNA的显式中心差分算法，对钢框架受冲击荷载的动态响应及破坏模式进行数值模拟，研究冲击质量、冲击速度、冲击位置参数对钢框架动态响应的影响，并探讨了钢框架在冲击荷载下的破坏形态。

1 数值模拟

1.1 模型简介

钢框架采用Q235的热轧H型钢，柱净高3 m，梁净宽3 m。柱的截面尺寸设为302 mm×294 mm×12 mm×12 mm，梁的截面尺寸设为204 mm×200 mm×12 mm×12 mm。梁与柱的节点采用全焊缝节点，通过ANSYS/LS-DYNA的glue命令流实现。柱顶端采用自由约束，柱脚端为固定约束。

冲击质量块的尺寸为H×B×L为500 mm×302 mm×1 500 mm。可通过调节冲击质量块的质量密度，来实现改变冲击质量。为了保证结构的动能全部由钢框架吸收或耗散，把冲击质量块约束为刚体。冲击质量块在速度V运动方向移动，沿R柱强轴方向冲击钢框架。框架模型见图1。

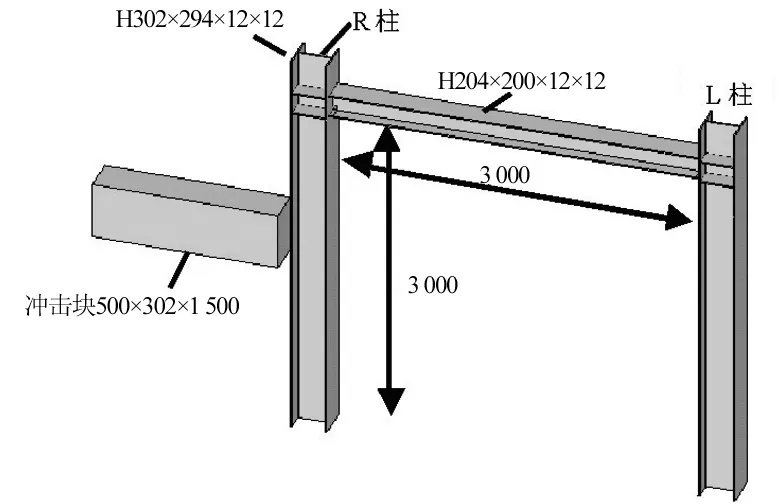
图1 钢框架模型(单位：mm)Fig.1 Model of steel frame(unit:mm)

本文的分析参数包括：冲击质量T设为3种情况：1、3、6 t；冲击速度V设为4种情况：5、10、15、20 m/s；冲击位置L设为2种情况：1、1.5 m；L代表柱脚到达冲击区域下边缘的距离。文中出现 1T10V1L表示冲击质量T=1 t、冲击速度V=10 m/s、冲击位置L=1 m，其余类推。

1.2 钢材本构模型

Q235钢材料模型采取Cowper-Symond等效强化模型，其本构关系为：

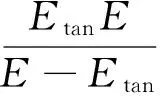
关于钢材的力学性能，其中弹性模量E为2.06×105 MPa，剪切模量Etan为1.18×103 MPa，Q235钢的静力屈服强σ0为235 MPa，参数C为40.4，参数β为1。

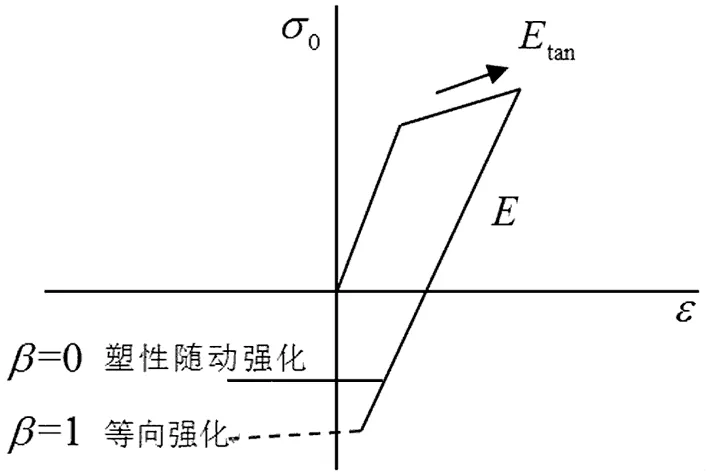
图2 Cowper-Symonds模型Fig.2 Model of Cowper-Symonds

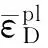
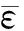
为了更好的得到模型在不同的冲击作用下的能量、冲击反力以及框架整体的应力分布情况，本文采用等效塑性应变值为0.34[7]。

1.3 网格划分

钢框架采用的单元为ANSYS/LS-DYNA单元库中的SOLID164单元，这是一种8节点6面体单元，单元没有实常数，精度和收敛性较高。同时采用多积分算法进行计算，这样可以有效地避免由于点积分产生单元计算不稳定，使结构在弯曲计算过程中容易产生刚度过于僵硬，导致单元退化，产生较大的沙漏能，使计算结果更加精确[7]。

为了划分较规格的单元，将钢框架和冲击质量块用ANSYS/LS-DYNA中映射网格对其整体划分，根据文献[8]，为了更好地提高计算效率，保证计算精度。将整个框架模型的划分网格尺寸设为60 mm，冲击碰撞区域网格尺寸设为20 mm。冲击块的单元尺寸取为50 mm。

2 动态响应分析

2.1 冲击力

通过用数值模拟，得到不同工况下的冲击力时程曲线和最大冲击力，并绘制最大冲击和速度相关曲线。

图3是冲击位置为1 m在不同冲击速度下冲击力时程曲线。由图3可知，只改变冲击速度，其余参数不变条件下，随着速度越大，冲击力的峰值越大，冲击持续时间越长。图4是冲击位置为1 m在不同冲击质量下冲击力时程曲线，表1是所有计算参数下的最大冲击力汇总表。由图4和表1可知，只改变冲击质量，其余参数不变时，随着冲击质量增加，整个模型的最大冲击力没有变化，但冲击时间增加。由此可得出，冲击速度影响最大冲击力，冲击质量对最大冲击力无影响。

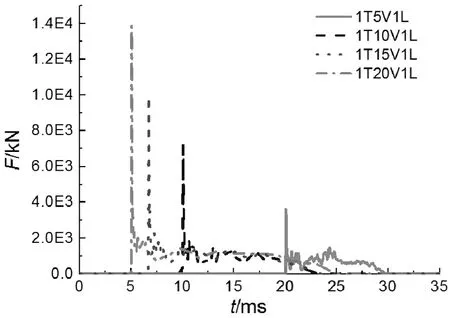
图3 冲击位置为1 m不同冲击速度下冲击力时程曲线Fig.3 The impact force-time history curves with different speeds at 1 m

图4 冲击位置为1m不同冲击质量下冲击力时程曲线Fig.4 The impact force-time history curves with different speeds at 1 m

图5是冲击位置为1.5 m时不同冲击速度下冲击力时程曲线。通过图5与图3、表1比较得到,当冲击位置在1.5 m，整个冲击过程会发生二次冲击，冲击位置1 m的最大冲击力和冲击位置1.5 m的最大冲击力基本不变。由此可知，冲击位置对整个结构冲击力最大值无影响。

图5 冲击位置为1.5 m不同冲击速度下冲力时程曲线Fig.5 The impact force-time history curves with different speeds at 1.5 m

通过以上参数分析和比较可知,影响整个结构冲击最大值的主要因素是冲击质量块速度。通过图6最大冲击力与速度的关系曲线图，拟合得到最大冲击力和冲击速度相关方程：

Fmax=671.656 6v+275.365R2=0.992 64 (3)

其中,R2是相关指数，其值越接近1，表明Fmax和v线性关系越强。

表1 最大冲击力Tab.1 Maximum impact force

注：表中1T10V1L表示质量T=1 t、冲击速度V=10 m/s、冲击位置L=1 m的参数组合，其余类推。

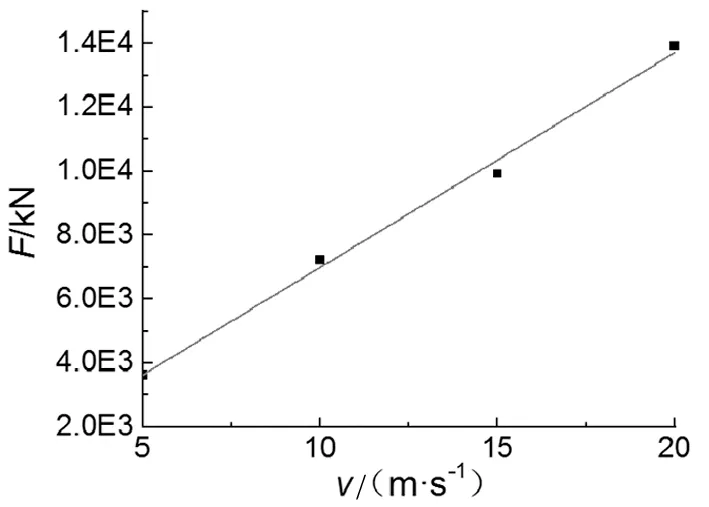
图6 最大冲击力和速度关系曲线Fig.6 Relation curves of maximum impact force and speed

2.2 位移

图7是冲击位置为1 m在不同冲击速度下L柱1/2处位移时程曲线，图8是冲击位置为1 m在不同冲击速度下R柱柱顶位移时程曲线。从图7、8可看出，冲击速度在20 m/s(72 km/h)以内，随着冲击速度的增加，整个模型的L柱1/2处的水平位移峰值及残余位移逐渐增加。如速度从5 m/s(18 km/h)增至10 m/s(36 km/h)时，L柱1/2处的水平位移最大值增幅为35.67 mm，R柱柱顶水平位移最大值增幅为37.28 mm；速度从10 m/s(36 km/h)增至15 m/s(54 km/h)时，L柱1/2处的水平位移最大值增幅为46.98 m，R柱柱顶水平位移最大值增幅为43.22 mm；速度从15 m/s(54 km/h)增至20 m/s(72 km/h)时，L柱1/2处的水平位移最大值增幅64.37 mm，R柱柱顶水平位移最大值增幅为48.18 mm。说明冲击速度越大，激起结构的反应越大；随着速度增加，钢框架塑性区域发展越来越快。通过图7、8比较可看出，未受冲击侧R柱也受冲击影响，但残余水平变形相对受冲击L柱处要小。

图7 冲击位置为1 m不同冲击速度下L柱1/2处位移时程曲线Fig.7 Lateral displacement-time history curves of mid L column with different speeds at 1 m

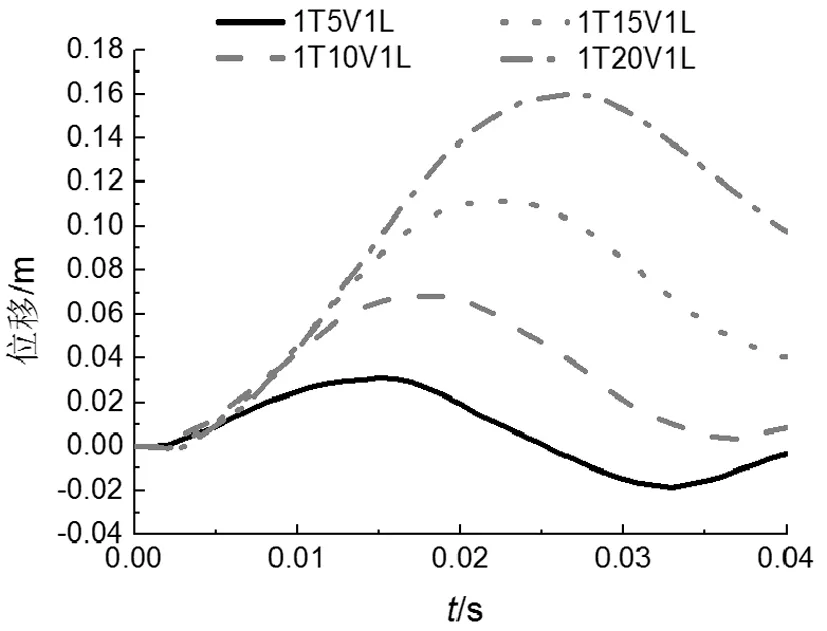
图8 冲击位置为1m不同冲击速度下R柱柱顶位移时程曲线Fig.8 Lateral displacement-time history curves of top R column with different speeds at 1 m

图9是冲击位置为1 m在不同冲击质量下L柱1/2处的位移时程曲线，图10是冲击位置为1 m在不同冲击质量下R柱柱顶位移时程曲线，从图9、10可见，冲击质量在6 t以内，随着冲击质量增加，整个模型L柱1/2处的水平位移峰值及残余位移逐渐增加。当1 t增至3 t时，L柱1/2处的水平位移最大值增幅为265.38 mm，R柱柱顶水平位移最大值增幅为217.20 mm；当3 t增至6 t时，L柱1/2处的水平位移最大值增幅为248.10 mm，R柱柱顶水平位移最大值增幅为48.20 mm，说明冲击质量越大，激起结构的反应越激烈；在相同质量增幅情况下，峰值位移增幅及残余位移增幅均呈递减之势，钢框架塑性区域发展速度减缓。通过比较图9、 10可以发现，未受冲击侧R柱也受冲击影响，而且得到受冲击侧L柱的冲击响应比未受冲击侧L柱的冲击响应更加激烈。

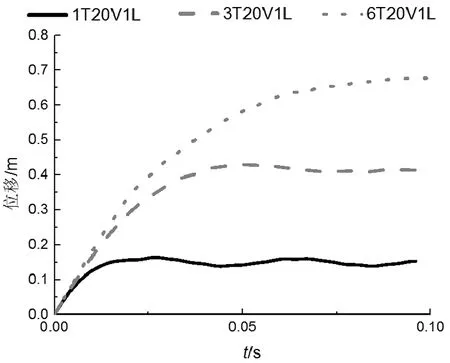
图9 冲击位置为1m不同冲击质量下L柱1/2处位移时程曲线Fig.9 Lateral displacement-time history curves of mid L column with different masses at 1 m

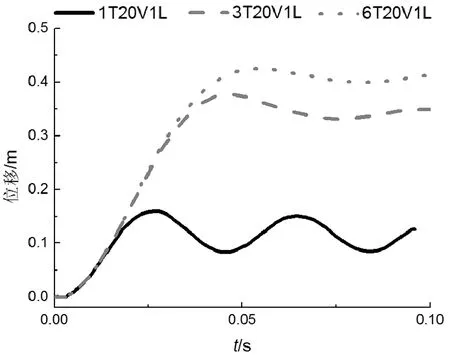
图10 冲击位置为1m不同冲击质量下R柱柱顶位移时程曲线Fig.10 Lateral displacement-time history curves of top R column with different masses at 1 m

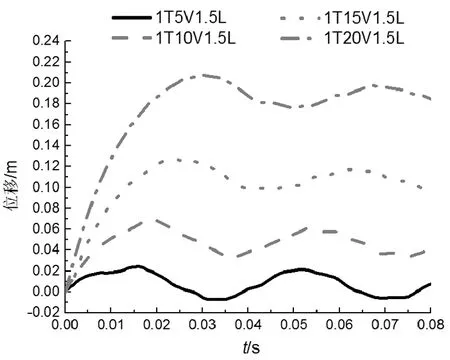
图11 冲击位置为1.5 m不同冲击速度下L柱1/2处位移时程曲线Fig.11 Lateral displacement-time history curves of mid L column with different speeds at 1.5 m

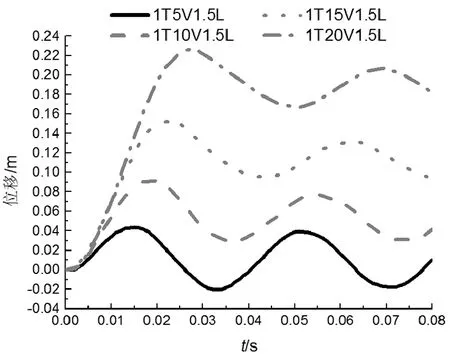
图12 冲击位置为1.5 m不同冲击速度下R柱柱顶位移时程曲线Fig.12 Lateral displacement-time history curves of top R column with different speeds at 1.5 m

图11是冲击位置为1.5 m在不同冲击速度下L柱1/2处的位移时程曲线，图12是冲击位置为1.5 m在不同冲击速度下R柱柱顶位移时程曲线。通过图7、11比较发现，速度为5 m/s时，冲击位置为1.5 m的L柱1/2处的最大水平位移比冲击位置为1 m的L柱1/2处的最大水平位移增加12.61 mm；速度为10 m/s时，冲击位置为1.5 m处L柱1/2处的最大水平位移比冲击位置为1 m处的L柱1/2处的最大水平位移增加24.25 mm；速度为15 m/s时，冲击位置为1.5 m处L柱1/2处的最大水平位移比冲击位置为1 m处的L柱1/2处的最大水平位移增加40.81 mm；速度为20 m/s时，冲击位置为1.5 m处L柱1/2处的最大水平位移比冲击位置为1 m处的L柱1/2处的最大水平位移增加66.70 mm。通过图8、 12比较发现，速度为5 m/s时，冲击位置为1.5 m处R柱顶最大水平位移比冲击位置为1 m处的R柱柱顶最大水平位移增加7.13 mm；速度为10 m/s时，冲击位置为1.5 m处R柱顶最大水平位移比冲击位置为1 m处R柱柱顶最大水平位移增加16.07 mm；速度为15 m/s时，冲击位置为1.5 m处R柱顶最大水平位移比冲击位置为1 m处的R柱柱顶最大水平位移增加27.27 mm；速度为20 m/s时，冲击位置为1.5 m处R柱顶最大水平位移比冲击位置为1 m处的R柱柱顶最大水平位移增加43.38 mm。这说明冲击质量块在冲击位置为1.5 m处响应激烈。这是因为相同冲击速度在冲击位置为1.5 m处对柱底产生弯矩比在冲击位置为1 m处的大，导致冲击位置在1.5 m处柱底由于弯矩产生转角比冲击位置在1 m处大。

3 破坏形态分析

根据有限元模拟结果，钢框架在冲击作用下破坏形态如图13。破坏形态主要特征为整个框架发生侧移，受冲击柱在冲击区域翼缘处出现局部屈曲，受冲击区域的截面发生弯扭，受冲击柱在冲击区域的翼缘和腹板产生单元失效，钢梁出现弯曲，未受冲击的柱出现倾斜，柱脚出现屈曲。这说明在冲击荷载作用下钢框架的破坏形态是由于结构受到冲击荷载的水平力与框架产生弯扭应力共同作用下导致的结果。

这种破坏形态对应的计算参数是3T20V1L 、6T20V1L。通过比较所有参数模型，可以发现，破坏形态的出现和冲击块的质量和速度相关。又因为冲击块的动能是由冲击块质量和速度共同决定，所以可以表明，破坏形态与整个结构的冲击动能相关。

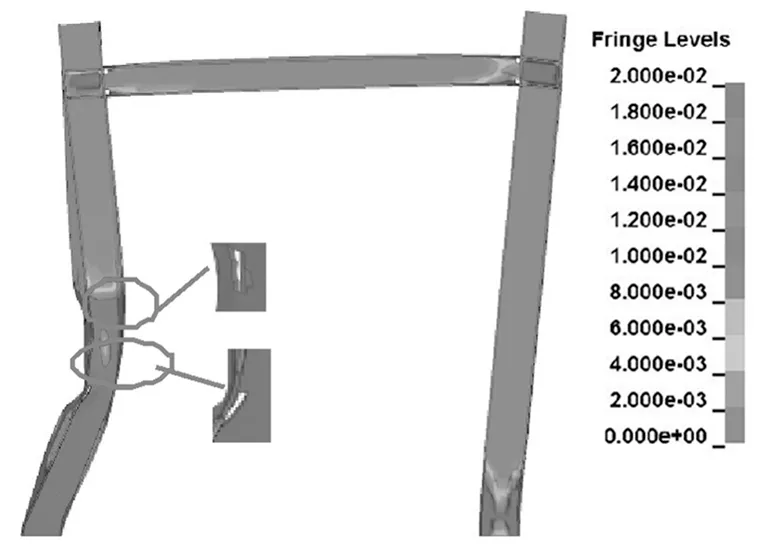
图13 冲击作用下钢框架破坏形态Fig.13 Failure modes of steel frame under impact

为更加清楚地表达一榀钢框架在受横向冲击作用下破坏损伤过程。以冲击速度为20 m/s、冲击块质量为3 t、冲击位置为1 m所对应的计算模型为研究对象。如图14，当计算时间到达0.006 s时，冲击体和钢框架刚接触，受冲击的L柱在冲击区域产生塑性区域，且塑性区域发生在冲击区域的腹板处，冲击区域的翼缘板处发生屈曲，R柱和梁上未出现塑性应变；当计算时间到达0.013 s时，整个钢框架发生明显侧移，受冲击侧L柱发生翼缘板屈曲、腹板鼓屈、截面弯扭破坏，连接梁发生弯扭现象，未受冲击R柱发生倾斜，柱脚屈曲变形；当计算时间到达0.034 s，整个冲击过程结束，出现框架整体侧移，受冲击柱子在冲击区域翼缘处出现局部屈曲、整个截面发生弯扭、翼缘出现破坏，受冲击柱子在冲击区域的腹板也产生破坏，连接梁出现弯曲，未受冲击的柱子出现倾斜，R柱和L柱的柱脚都出现屈曲。

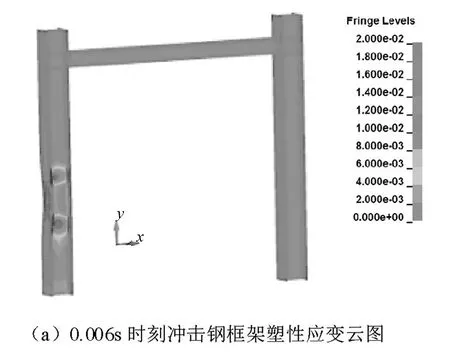
由图14可知，在冲击荷载作用下，因为冲击的时间极短，冲击力峰值大，所以一榀钢框架的破坏具有局部性，高应变主要集中在被冲击柱子的冲击区域，距离冲击区域较远的柱脚处和梁柱节点没有发生太大损伤。

4 结论

1)利用非线性显式动力学有限元分析方法，对冲击荷载作用下钢框架的动态响应和破坏形态进行了研究。采用的SOLID164单元没有实常数，精度和收敛性较高，同时采用多积分算法进行计算，可以有效避免由于点积分产生单元计算不稳定、使单元退化而产生较大的沙漏能，以保障计算结果的可靠性。

2)冲击体的质量、速度的增加和冲击位置的改变都会不同程度加剧钢框架的动态响应。在其它条件不变的情况下，随着冲击速度的增加，L柱1/2和R柱柱顶处水平位移的响应峰值呈现增加趋势；其它条件不变情况下，冲击质量的增加，L柱1/2和R柱柱顶处水平位移峰值增加；且在相同质量增幅情况下峰值位移增幅呈递减之势；冲击体的位置从1 m提高到1.5 m，在其它条件不变的情况下,L柱1/2和R柱柱顶处水平位移峰值增加。

3)在冲击荷载作用下，钢框架破坏形式表现为框架的整体侧移，局部破坏形式表现为翼缘的出现局部屈曲，受冲击区的截面发生扭转，高应变主要出现在被冲击柱子的冲击区域、柱脚处和梁柱节点处。

4)分析钢框架冲击荷载作用下的应变云图可以发现，框架的塑性应变是从受冲击处向柱脚和梁柱连接点处传递，受冲击侧柱塑性变形的速度明显快于未受冲击侧柱。

[1] Nagel G M,Thambiratnam D P.Dynamic simulation and energy absorption of tapered thin-walled tubes under oblique impact loading[J].International Journal of Impact Engineering,2006,32(10):1595-1620.

[2] Heng P,Hjiaj M,Battini J M,et al.A simplified model for nonlinear dynamic analysis of steel column subjected to impact [J].International Journal of Non-Linear Mechanics,2016,86:37-54.

[3] 朱斌，陈仁朋，罗军.低速运动船只撞击埋置框架结构动力分析模型[J].海洋工程，2008，26(2)：17-25.

[4] 霍静思，张晋清，陈柏生，等．冲击荷载作用下热轧H型钢梁力学性能试验研究[J]．建筑结构学报，2011，32 (12) :242-249．

[5] Pei Chang，Wang Rui． Parametric analysis of the dynamic response of hot-rolled H-shaped steel beam under lateral impact load[J].Applied Mechanics and Materials,2012,215-216:998-1002．

[6] 张峰峰，殷福新.基于LS-DYNA刚性钢框架受撞击整体性能的有限元分析[J].中国新技术新产品,2009(18):21.

[7] 宿专青.削弱型钢框架在冲击荷载作用下的数值分析[D].大连:大连理工大学，2012.

[8] Makarem F S,Abed F.Nonlinear finite element modeling of dynamic localizations in high strength steel columns under impact[J].International Journal of Impact Engineering,2013,52:47-61.

(责任编辑：陈雯)

Dynamicresponseanalysisofsteelframesubjectedtoimpactload

Yang Mianyue1，Fu Chaojiang1，2，Chen Hongjun1

(1.College of Civil Engineering,Fujian University of Technology,Fuzhou 350118,China;2.Fujian Provincial Key Laboratory of Advanced Technology and Informationization in Civil Engineering,Fuzhou 350118,China)

The process of dynamic response for steel frame subjected to impulsive load is a complicated nonlinear problem.A three-dimensional model of the steel frame was established using ANSYS/LS-DYNA finite element analysis software.The dynamic response and failure modes of the steel frames under impact loading were studied.Multi-point integration algorithm was adopted to avoid hourglass problem effectively and to ensure accurate calculation results.Taking the collision of impact block and steel frame as an example,the effect of impact velocity,impact mass and impact position on the dynamic response of the steel frame were analysed,and the failure mode of the steel frame under impact was discussed.With the increase of impact mass,impact velocity and impact position,the dynamic response of the steel frame increases.High strain mainly occurs at the impact area,the bottom of the column and the beam column joints.The failure mode of the steel frame under the impact load is lateral displacement of the whole frame.Local buckling occurs at the flange of the impact column,bending-torsion takes place at the section of the impacted area,and tilting appears in the another column.

impact load;steel frame;multi-point integration algorithm;dynamic response;failure mode

TU398.9

A

1672-4348(2017)04-0317-07

10.3969/j.issn.1672-4348.2017.04.003

2017-05-16

国家自然科学基金项目(51378124))

付朝江(1966-)，男，江西九江人，教授，博士，主要研究方向：钢结构理论及结构数值分析。