T形配钢型钢混凝土偏压构件力学性能研究
郑永乾,赖鹏松,郑莲琼
(1.福建省土木工程新技术与信息化重点实验室,福建 福州 350118;2.福州大学 土木工程学院,福建 福州 350116)
T形配钢型钢混凝土偏压构件力学性能研究
郑永乾1,2,赖鹏松1,郑莲琼1
(1.福建省土木工程新技术与信息化重点实验室,福建 福州 350118;2.福州大学 土木工程学院,福建 福州 350116)
建立了T形配钢型钢混凝土偏压构件力学性能分析的有限元模型,计算结果得到以往实验结果的验证。在此基础上,分析了不同阶段材料应力状态和各参数对偏压构件力学性能的影响。结果表明:T形配钢型钢混凝土构件在不同加载角下的性能有所不同,加载角为180°时极限承载力大于其他角度情况;混凝土抗压强度、型钢含钢率、配筋率、荷载偏心率、长细比对构件荷载-变形曲线的影响较大,随着混凝土强度、型钢含钢率、配筋率的增加,极限承载力和刚度增加;随着荷载偏心率的增加,极限承载力和刚度下降;随着构件长细比的增加,构件承载力总体呈现线性下降趋势,刚度下降明显。
T形配钢; 型钢混凝土; 偏压构件; 有限元
型钢混凝土柱具有良好的受力性能,在工程中的应用非常广泛。当型钢混凝土用于边柱时,可采用T形配钢以便于节点的连接。以往对型钢混凝土力学性能的研究主要集中在配置工字型钢和十字型钢的构件,取得了不少研究成果[1-2],但对T形配钢型钢混凝土构件的研究尚不够系统。由于T型钢只是单轴对称,其受力与其他对称配钢型钢混凝土不同,因此研究T形配钢型钢混凝土构件的力学性能非常重要。
Nishimura等[3]进行了6个T形配钢型钢混凝土柱的滞回性能试验,试验主要参数为轴压比和加载角,结果表明,该类构件具有较大的能量耗散能力,加载角对正向和反向(正向为推力,反向为拉力)反复加载的抗弯承载力影响显著。王彦斌[4]进行了12个非对称配钢型钢混凝土柱在地震作用下的滞回性能试验,内配型钢截面形式为T型和L型,最后建立了构件恢复力模型。赵程程[5]进行了24个非对称配钢的型钢混凝土柱滞回性能试验,主要参数为配钢形式、配箍形式、配箍率、轴压比、剪跨比,给出了构件轴压比限值的建议值。曾磊等[6]、王秋维和史庆轩[7]提出了T形配钢型钢混凝土柱的正截面承载力计算方法。曾磊等[8]进行了12个T形配钢型钢混凝土柱的水平低周往复荷载试验,分别给出了T形配钢型钢混凝土柱在剪切斜压破坏和剪切粘结破坏的受剪承载力的计算方法。曾磊等[9]进行了24根非对称配钢型钢混凝土柱在往复荷载下的试验,内配型钢截面形式为T型和L型,最后建立了三线型刚度退化模型。
可见,对T形配钢型钢混凝土柱在偏压作用下的性能研究尚少见报道,尤其在双向受力下的偏压性能研究更是缺乏。为此,本文采用ABAQUS软件建立了分析T形配钢型钢混凝土压弯构件力学性能的有限元模型,并将计算结果与以往相关试验结果对比,验证有限元模型的可靠性。在此基础上,分析了偏压作用下不同阶段混凝土应力状态,并进行了各重要参数对荷载-变形全过程曲线的影响分析,参数主要包括混凝土强度、型钢屈服强度、含钢率、钢筋屈服强度、配筋率、加载角、荷载偏心率、长细比,从而为进一步提出科学合理的设计方法创造条件。
1 有限元建模
采用ABAQUS有限元软件进行分析,柱截面如图1所示。由于柱高方向的对称性,取柱高一半模型,如图2所示。为了更清楚看到型钢和纵筋、箍筋的模型,去除部分混凝土,构件端部设置刚性端板。
T型钢、纵筋和箍筋采用ABAQUS提供的等向弹塑性模型,应力-应变关系参见韩林海[10]提供的表达式。混凝土采用塑性损伤模型,受压应力-应变关系采用Attard和Setunge[11]提供的表达式。型钢采用壳单元S4R模拟,纵筋和箍筋采用三维杆单元T3D2模拟,混凝土、刚性端板采用三维实体单元C3D8R模拟。型钢端部与刚性端板采用shell-to-solid coupling连接,混凝土与刚性端板采用Tie连接,T型钢、纵筋和箍筋全部嵌入到混凝土中。刚性端板加载线处约束XY方向位移,并采用位移加载模式,施加Z向位移。

图1 T形配钢型钢混凝土截面Fig.1 T-shaped steel reinforced concrete section

图2 有限元模型Fig.2 Finite element model
2 模型验证
由于T型配钢型钢混凝土偏压构件试验研究较少,为了验证模型准确性,本文将配工字型钢的型钢混凝土偏压构件试验结果、T形配钢型钢混凝土的滞回骨架线试验结果与有限元模拟结果进行比较。
叶列平[12]报道了16个配工字型钢I10的型钢混凝土偏压柱试验结果,其中,截面边长B=160 mm,型钢屈服强度fy=312.5 MPa,纵向受力钢筋4根直径9 mm,屈服强度fyb=300.2 MPa,混凝土立方体强度fcu为34.3~53.57 MPa,试验考察的主要参数为长度L/边长B为9.375~18.75,荷载偏心率e/r为0.094~2.0(其中r=B/2),图3给出部分偏压构件计算结果与实验结果对比情况。
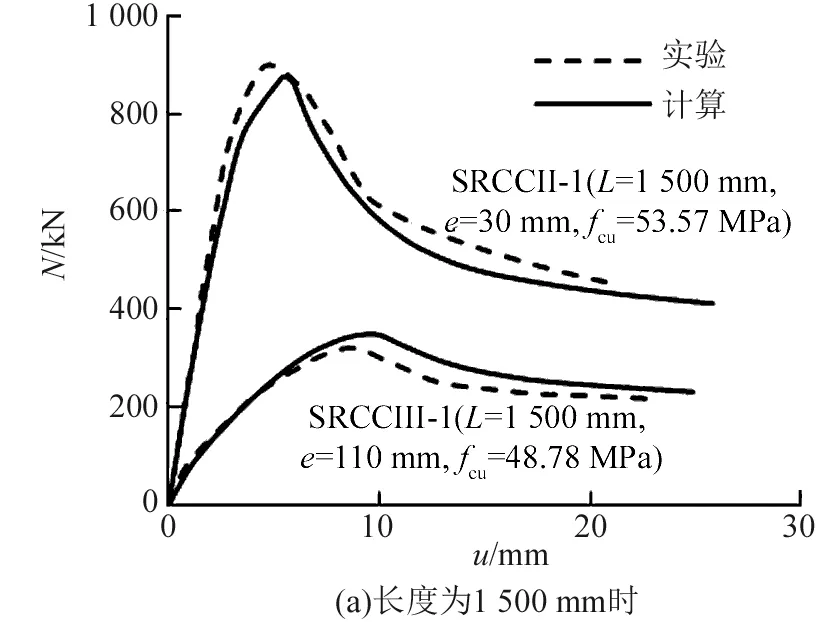

图3 配工字钢的型钢混凝土构件计算与试验结果对比Fig.3 Comparison between the calculation results and the experimental results of I-shaped steel reinforced concrete member
滞回骨架曲线往往与单调加载时的荷载-变形曲线一致,本文也对Nishimura等[3]进行的T形配钢型钢混凝土构件进行计算,其不同加载角度θ(0°、45°和90°)时的弯矩M-转角R骨架线与有限元单调计算结果如图4所示。其中,柱截面为250 mm×250 mm,图4(a)~(c)所示构件的轴力为压力,荷载比nc=0.4,图4(d)~(f)所示构件的轴力为拉力,荷载比nt=0.15。

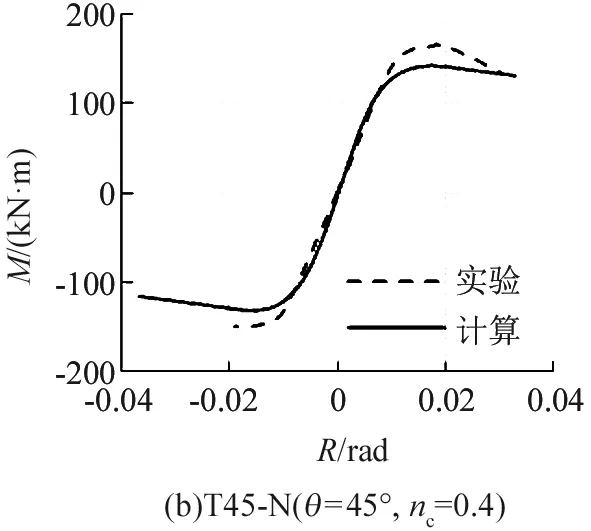
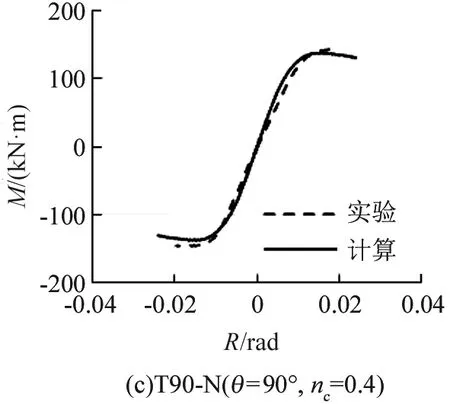
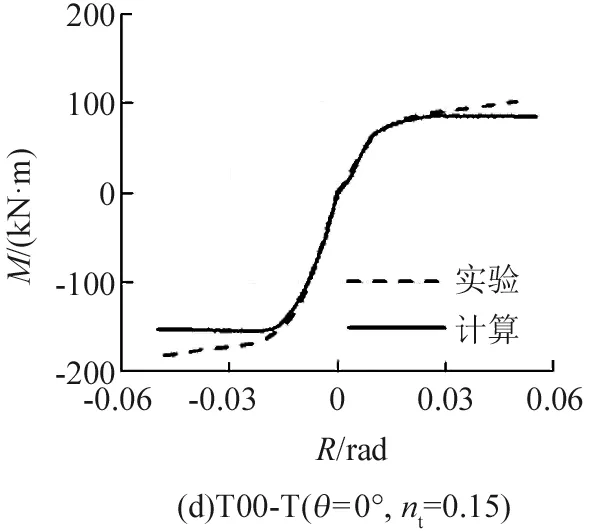
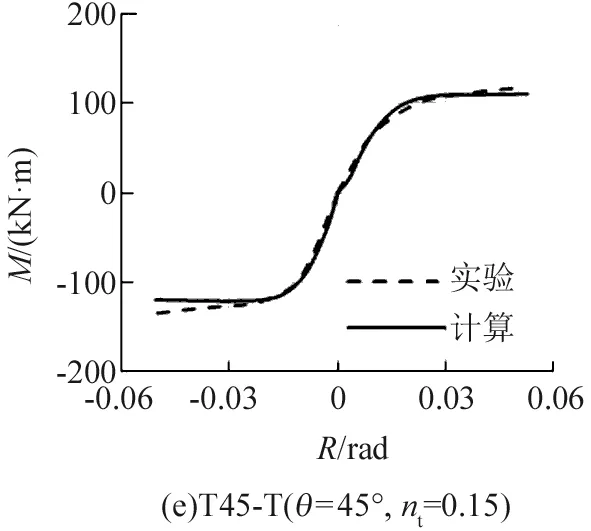
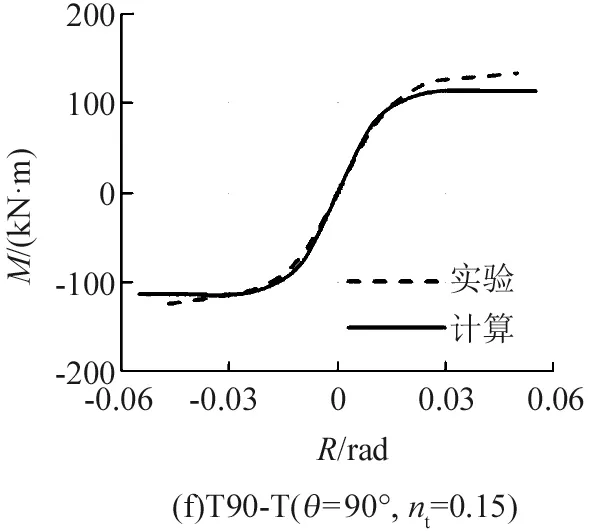
图4 T形配钢型钢混凝土的滞回骨架线与计算结果比较Fig.4 Comparison between hysteresis skeleton curves and the experimental results of T-shaped steel reinforced concrete member
3 应力分析
本文选取型钢混凝土柱截面:截面边长B=800 mm,内部T形配钢由工字钢I-500×200×20×16和型钢T-400×200×20×16组合而成;配置12根直径28 mm的纵向受力钢筋,箍筋直径16 mm,间距200 mm。型钢表面至混凝土表面的距离为150 mm,纵向受力钢筋中心至截面外表面的距离为70 mm,角部相邻纵向钢筋中心间距为80 mm。型钢屈服强度fy=345 MPa,钢筋屈服强度fyb=400 MPa,混凝土立方体抗压强度fcu=50 MPa,柱高L=9 238 mm,即长细比λ=40,偏心距e=200 mm,其中,图1X轴正向的荷载偏心距为正值,反之为负值。
图5所示为荷载N-跨中挠度u关系曲线,为考察混凝土应力,在曲线上取特征点A、B、C,其中A为钢材屈服强度达到比例极限时刻;B为极限承载力对应点;C为荷载下降到82%极限承载力对应点。
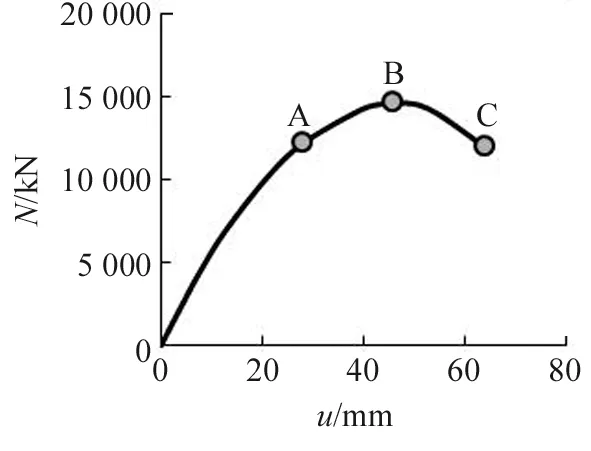
图5 荷载-跨中挠度关系曲线Fig.5 Load-mid-span deflection relationship
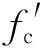
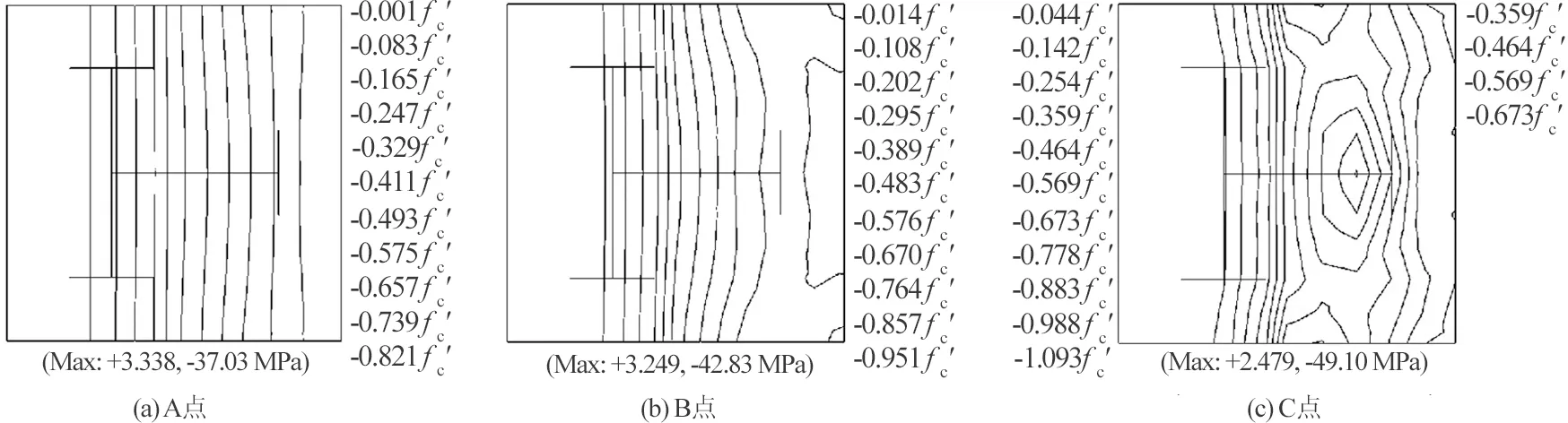
图6 不同时刻混凝土纵向应力Fig.6 The concrete longitudinal stress at different times
4 参数分析
基于以上模型,分别研究了混凝土抗压强度、型钢屈服强度、型钢含钢率、钢筋屈服强度、配筋率、加载角、荷载偏心率、长细比对荷载-变形关系曲线的影响,如图7所示。
4.1 混凝土抗压强度fcu
混凝土抗压强度对构件承载力和刚度的影响显著,如图7(a)所示。随着混凝土强度的增加,极限承载力明显增加,混凝土立方体抗压强度为50 MPa和70 MPa的极限承载力分别比30 MPa构件承载力提高了35.1%和74.7%,而且随着混凝土抗压强度的增加,构件刚度也提高,但由于混凝土塑性性能下降,因而构件延性变差。
4.2 型钢屈服强度fy
随着型钢屈服强度的提高,型钢能够承受更大的荷载,构件极限承载力提高,但由于在达到峰值荷载的时候,型钢仅有右侧部分区域接近屈服强度,因而提高幅度不大,型钢屈服强度为420 MPa时的构件极限承载力仅比型钢屈服强度为235 MPa时的构件承载力提高4%,如图7(b)所示。由于不同屈服强度型钢的弹性模量相同,因而不影响构件刚度。
4.3 型钢含钢率α
型钢含钢率越大,型钢的体积就越大,在荷载作用下有更多的钢材发挥作用,构件承载力和刚度提高较明显,总体呈现线性增长的趋势,同时,极限承载力对应的跨中挠度有所增加,如图7(c)所示,含钢率为0.12的极限承载力和刚度分别比含钢率为0.08的构件提高14.6%和7.5%。
4.4 钢筋屈服强度fyb
和型钢屈服强度影响规律一致,钢筋屈服强度对构件的刚度没有影响,对极限承载力的影响不大,如图7(d)所示。
4.5 配筋率ρ
配筋率对构件的承载力影响较大,随着配筋率的增加,受力过程中钢筋能够承受更大荷载,其承载力和刚度均增加,如图7(e)所示。配筋率从0.026到0.0462构件刚度增加17%,承载力增加20%。
4.6 加载角θ
图7(f)为加载角对构件荷载-变形曲线的影响情况,加载角θ为加载点至中心点连线与X轴正方向的夹角(如图1)。可见,当加载角为45°和135°时,构件极限承载力均有所减小,当加载角为90°时,偏心一侧的左侧型钢上翼缘和腹板发挥作用,使得极限承载力有所提高,在加载角为180°时,竖向荷载作用靠近左侧型钢,左侧型钢体积较大,有更多钢材发挥作用并承担荷载,极限承载力最大,比加载角为0°构件承载力提高11%。从构件刚度上看,加载角的总体影响很小。
4.7 荷载偏心率e/r
荷载偏心率e/r(r=B/2)对构件刚度和承载力的影响十分显著,如图7(g)所示,正值为X轴正向偏心,负值为X轴反向偏心。随着荷载偏心率的增加,构件在变形过程中的二阶效应越明显,刚度和极限承载力下降,极限承载力在偏心率≤0.5时下降迅速,而后下降速率有所减小,例如荷载偏心率为0.25、0.5、0.75、1的极限承载力分别为荷载偏心率0时承载力的62.7%、43.4%、32.6%和26.1%,极限荷载对应的跨中挠度也不断增加;当荷载偏心率数值相同时,负值实际上为加载角为180°的情况,荷载作用一侧更多型钢发挥作用,总体上极限承载力比正向偏心的高,在e/r为1和-1情况下的极限承载力非常接近。
4.8 长细比λ
随着构件长细比的增加,构件在荷载作用下更容易发生变形,有更多材料单元快速进入塑性状态,构件承载力下降,极限荷载对应的跨中挠度明显增加,例如,长细比每增加10,构件极限承载力大致下降7%,总体呈现线性下降规律,而刚度下降幅度比承载力下降幅度大得多,长细比为40~60的构件刚度为长细比30构件的56.3%~25.1%,如图7(h)所示。




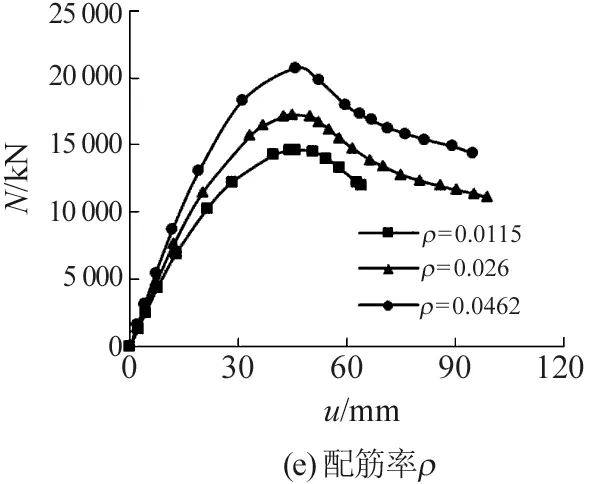

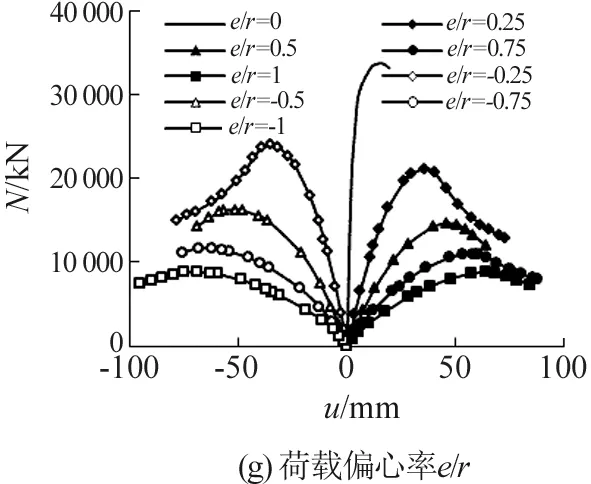
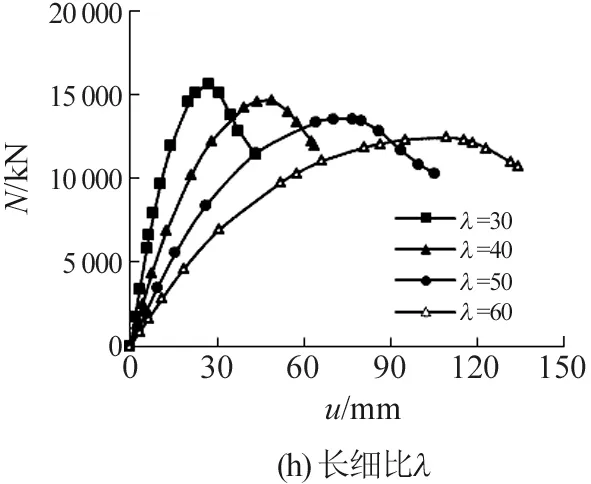
图7 各参数对荷载-变形关系曲线的影响Fig.7 The influence of parameters on load-deformation relation curve
5 结论
1)建立了T形配钢型钢混凝土构件在压弯情况下力学性能的有限元模型,通过对比相关试验结果,验证了有限元模型的可靠性,在此基础上分析了受力过程中混凝土的应力状态。
2)由于T形配钢截面仅为单轴对称,加载角对构件极限承载力有一定影响,在工程常用参数范围内,当加载角为180°时极限承载力大于其他角度情况。
3)随着型钢屈服强度或钢筋屈服强度的提高,构件极限承载力提高,但提高幅度不大,基本不影响构件刚度。
4)混凝土抗压强度、型钢含钢率、配筋率、荷载偏心率、长细比对构件荷载-变形曲线的影响较大,随着混凝土强度、型钢含钢率、配筋率的增加,极限承载力和刚度增加;随着荷载偏心率的增加,极限承载力和刚度下降。随着构件长细比的增加,构件承载力总体呈现线性下降趋势,刚度下降明显。
[1] Chen S W,Wu P.Analytical model for predicting axial compressive behavior of steel reinforced concrete column[J].Journal of Constructional Steel Research,2017,128(1):649-660.
[2] Zhu W Q,Jia J Q,Gao J C,et al.Experimental study on steel reinforced high-strength concrete columns under cyclic lateral force and constant axial load[J].Engineering Structures,2016,125(10):191-204.
[3] Nishimura Y,Tsutsui S,Baba N.Flexural behavior of steel reinforced concrete columns with T-shaped steel[C]//13thWorld Conference on Earthquake Engineering,Vancour,Brltish Columbia,Canada,August 1-6,2004.Vancouver:s.n.,2004:1338-1345.
[4] 王彦斌.非对称配钢型钢混凝土柱抗震性能试验研究[D].荆州:长江大学,2012.
[5] 赵程程.非对称配钢型钢混凝土柱轴压比限值研究[D].荆州:长江大学,2012.
[6] 曾磊,涂祥,吴园园.T形配钢型钢混凝土构件正截面承载力计算方法[J].工程力学,2013,30(10):115-121,132.
[7] 王秋维,史庆轩.T形型钢混凝土柱正截面承载力的计算方法探讨[J].力学与实践,2008,30(5):24-27.
[8] 曾磊,周琴,吴园园,等.非对称配型钢混凝土柱受剪机理及承载力研究[J].建筑结构,2014,44(4):30-34,43.
[9] 曾磊,吴园园,周琴,等.循环荷载作用下非对称配钢型钢混凝土柱性能退化试验[J].兰州理工大学学报,2014,40(6):124-130.
[10] 韩林海.钢管混凝土结构——理论与实践[M].2版.北京:科学出版社,2007.
[11] Attard M M,Setunge S.Stress-strain relationship of confined and unconfined concrete[J].ACI Materials Journal,1996,93(5):432-442.
[12] 叶列平.劲性钢筋混凝土偏心受压中长柱的试验研究[J].建筑结构学报,1995,16(6):45-52.
(责任编辑:陈雯)
BehaviourofT-shapedsteelreinforcedconcreteeccentricloadedcolumns
Zheng Yongqian1,2,Lai Pengsong1,Zheng Lianqiong1
(1.Fujian Provincial Key Laboratory of Advanced Technology and Informationization in Civil Engineering,Fuzhou 350118,China;2.College of Civil Engineering,Fuzhou University,Fuzhou 350116,China)
Finite element models for analysing the behaviour of T-shaped steel reinforced concrete eccentric loaded columns were established.The calculated results of the columns were validated by the previous experimental results.Furthermore,the material stress status at different stages and the effect of the relevant parameters on the mechanical behaviours of the columns were analysed.The results indicate that the T-shape steel reinforced concrete columns exhibit different performances at different load angles.The ultimate load bearing capacity at a load angle of 180° is higher than that of other load angles.The parameters such as concrete compressive strength,section steel ratio,steel reinforcement ratio,load eccentricity ratio and length to slenderness ratio exert significant influences on the load-deformation curves of the columns.With the increase of the concrete strength,the section steel ratio or the steel reinforcement ratio,the ultimate load bearing capacity and the stiffness increase.With the increase of the load eccentricity,the ultimate load bearing capacity and the stiffness decrease.With the increase of the length to slenderness ratio,the load bearing capacity has the tendency of linear decreasing in general with the stiffness dropping obviously.
T-shaped steel;steel reinforced concrete;eccentric loaded column;finite element
TU398.9
A
1672-4348(2017)04-0307-06
10.3969/j.issn.1672-4348.2017.04.001
2017-06-14
国家自然科学基金项目(51678151);福建省资助省属高校科研专项项目(JK2015029);福建省自然科学基金项目(2014J01171)
郑永乾(1979-),男,福建诏安人,教授,博士,研究方向:组合结构及防灾减灾。

