小学生问题解决的本真探讨

张秀花

【摘要】问题解决是数学教育改革的重点之一，引起广大教师的高度重视。教学时要引导学生学会从数学的角度去发现问题和提出问题，综合运用数学知识来解决简单的实际问题，获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，初步形成评价与反思的意识。

【关键词】小学数学；问题解决

问题解决是数学教育改革的重点之一，引起广大小学数学教师的高度重视。《新课标》（2011年版）在课程总目标指出：“初步学会从数学的角度发现问题和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力。获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识。学会与他人合作交流。初步形成评价与反思的意识。”在实际教学中，教师如何培养学生问题解决的能力，一直是很多数学教师的困惑。本文结合平时一线老师的教学案例，进一步探讨小学生问题解决的策略，和各位同仁商榷。

一、学会从数学的角度发现与提出问题

数学新教材，问题呈现的方式丰富多样，除文字叙述外，还有表格、图画、对话等方式，也适当增加了有多余条件和开放性的问题，向学生提供鲜活的、真实的、有趣味的和具有探索思考价值的数学问题，凸显应用题的问题特征。学生面对丰富多元的素材，需要搜集信息、整理信息、分析信息、处理信息。数学课堂教学，首先需要培养学生的提问能力，学会从数学的角度发现与提出问题，变“要我学”为“我要学”，对于真正提高学生素质有积极的作用。例如一位老师执教六年级下册《解决问题的策略》设计如下的教学环节。

首先，情境小故事导入。（视频欣赏：孟浩然与故友探讨鸡兔同笼问题）

接着，出示例题：全班42名同学去划船，一共租用了10条船，每条大船坐5人，每条小船坐3人，租用的大船和小船各有几条？

师：从图中你能获得哪些数学信息？

生：交流信息。

师：你准备怎样来解决这个问题？课前同学们已经对这一问题进行了预学，先请同桌相互交流一下你的思考。

生：同桌交流方法。

师：哪位同学先来展示一下你的方法。学生走上讲台展示。（同伴倾听，相互评价，师做好适度引领，相机指导）

其一，交流展示——画图策略。

生1：我用的是画图的策略，假设10条船全都是大船，总人数为50人，比实际多出8人，这时每条大船需减去2人，8人正好从4条大船上减掉，减掉2人的大船要换成小船，最后得出小船有4条，大船有6条。

师：刚才这位同学给我们展示了画图的策略，听了他的介绍，有什么问题吗？

生2：为什么每条大船只减去2人呢？

生1：因为每条大船比小船多坐2人。

师：还有谁愿意展示不一样的方法？

其二，交流展示——列举策略

生3：我用的是列举的策略，先假设大船9条，小船各1条，得到总人数48人，比实际42多6人，不断调整减少大船增加小船，最后得出大船6条，小船4条。

师：刚才这位同学给我们展示了列举的策略，观察列举过程，你有什么发现？

生4：我发现他的列举比较有序。

师：有序的列举有什么好处？

生5：有序的列举可以做到不重复、不遗漏。

师：还有谁愿意展示不一样的方法？

其三，交流展示——“假设—相等”策略

生6：我用的是“假设—相等”的策略，先假设大船小船条数相等各5条，得到总人数40人，比实际42人少2人，这就需要把大船增加1条小船减少1条，最后得到大船6条，小船4条。

师：刚才我们展示的列举策略和“假设—相等”策略都用到了表格来整理，比较一下你更喜欢哪种策略？

生7：我更喜欢“假设—相等”的策略，这种策略列举的次数更少，更方便。

师：还有不一样的方法吗？

其四，交流展示——计算方法

生8：我用的是计算的方法，假设全是大船：10×5=50（人），50-42=8（人）

5-3=2（人），8÷2=4（只），10-4=6（只），最后得到大船6条，小船4条。

师：下面请一位同学结合动态的演示来说一说每道算式的意思。

生9：结合课件动态的演示说一说每道算式表示的具体意思。

师：刚才我们研究坐船问题展示了不一样的策略和方法，尽管策略方法不一样，但它们的解题思考过程有一个相似的地方，你发现了吗？

生10：先假设，然后比较，再调整，最后验证。

师：同步板书假设、比较、调整、验证。

……

上述教学片断中，教者让学生先观察思考“从图中你能获得哪些数学信息？”进行收集信息、整理信息，然后组织学生交流信息，尔后提出“同桌相互交流一下你的思考”，同桌交流后走上讲台展示，通过对不同策略方法的自主展示与交流，让学生主动参与到学习中来，发现问题、提出问题、探究知识，结合对不同策略的展示，让学生在主动探究的过程中，进一步理解并掌握画图、列举、假设、调整等多种策略的解题过程，初步学会选择合适的策略分析数量关系、确定解题思路，并有效地解决问题；帮助学生在选择策略解决问题的过程中，初步体会策略的多样性，获得一些灵活运用策略解决问题的经验，增强策略意识，提高发现与提出问题的能力，感悟到“假设一比较—调整—验证”这样的解题思考方式，帮助学生建构数学模型，学会运用这种模型来解决同类问题，进一步感知体验策略的本质与价值。教学基于“双主体”课堂理念，让学生在预学引领下发现问题、提出问题、主动展示，从而做到自然地学、自主地学、自由地学。

二、学会分析与解决问题的基本方法

学生分析問题、解决问题能力的培养不是一蹴而就的，而是一个循序渐进的过程，在数学课堂教学中，结合具体的学习内容，逐步提高学生解决问题的能力。endprint

首先，读题审题，理解题意。不同年级的学生，读题审题指导也各有侧重。例如刚入学的一年级学生还认不了几个字，有些老师在读题时经常“一手包办”，于是学生的读题“形同虚设”，变成了听题，这不利于学生识字和读题能力的发展。因此，在学生刚入学的时候，老师要有意识地培养他们一边用自己的手点着字，一边读题的习惯。要求孩子们也像老师那样，手点一个字读一个字，做到手口一致。虽然在刚开始的一段时间里，可能会有部分孩子会走神，跟不上大家的节奏，而且比较耗时间，但只要老师耐心提醒，长期坚持，学生的识字量会快速增加，读题速度会越来越快，大大减少了学生因为不识字而影响理解题意的情况。

在学生能正确熟练地读题后，老师还要引导学生学会找题目中的关键词，也就是边读边圈。例如老师经常地让孩子们读题时找一找：在这道题中，要求是什么？你认为题中的哪些词很关键？请你圈出来，圈出关键字再多读几遍。例如在“白兔有23只，黑兔比白兔多15只，黑兔有多少只？”这道题中，最关键的是要读懂“黑兔比白兔多15只”这句，可以这样指导学生读题的：第一步，圈出句子里的“多”字；第二步，找出谁多，一般到“比”字的前面去找，找到“黑兔”后把它圈出来；第三步，读读圈出来的几个词。在这样边圈边读的过程中，不仅能提高学生的数学意识，也提高了学生捕捉信息数据的能力，为学生理解题意、提高解题能力奠定了初步的基石。

再如低年级教材中有很多图形结合题。对于这类题老师要引导学生正确、有序地看图，先整体了解图中的情境内容，再看图中的个别信息，尤其要留意隐含在画面中的一些数据信息，然后用自己的语言表述出题目中的已知条件和问题。

其次，帮助学生分析归纳数量关系。加强数量关系的分析与理解是提高学生解决问题能力的关键。例如低年级老师可以帮助学生归纳出几类简单的数量关系：简单的加、减、乘、除数量关系；知道其中的两部分求总量的关系；知道总量、其中一部分求另一部分的关系；求一个数比一个数多（少）几的关系；求几个数的和的简单的乘法关系等。学生可以思考利用所总结的数量关系去解决问题。对于中高年级的学生，结合数学教材内容编排，引导学生理解并掌握“速度、时间、路程”相互之间的数量关系以及“单价、数量、总价”相互之间的数量关系。

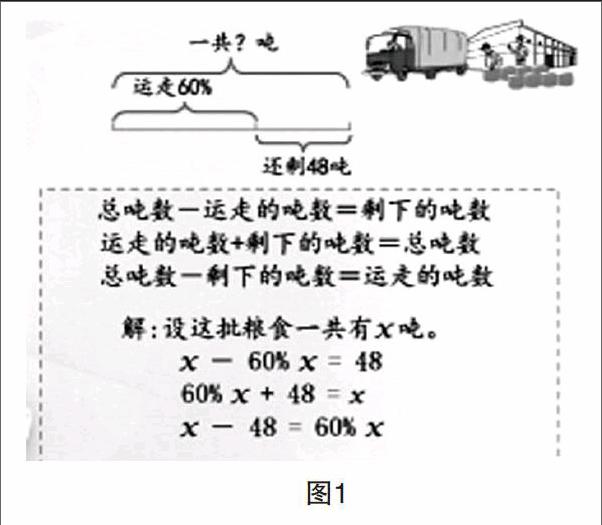
其三，灵活选择方法解决问题。例如《列方程解决稍复杂的百分数实际问题1》是百分数单元的教学难点。很多老师备课时，有过这样的困惑：“要不要让学生画线段图？”“学生对数量关系式的理解较为容易的，列出的方程却和数量关系式不符”等。一位老师巧用线段图来设计百分数实际问题，根据数量关系式的特点，确定列方程来解决实际问题。学生依据不同的数量关系式，列出不同的方程，并在观察、比较中优化方程，这是列方程解决稍复杂百分数实际问题非常重要的一个环节。通过优化方程，加深学生对数量关系的理解，突出教学重点，分解教学难点，化难为易，层次分明，思路清晰。通过列方程解答，让学生感受到解决问题的一般过程。

如图1所示，观察线段图，学生分析出单位“1”未知时，由已有的知识经验，学生可以很快想到用方程去解。这里的粮食总吨数和已运走粮食的吨数都是未知，2个未知量，如果设总吨数是x，那么已经运走的吨数就是60%x。让学生在学习单上列出方程，不解答。交流学生不同的方程，可能有：x-60%x=48；60%x+48=x； x-48=60%x。也有的学生出现第四种（1-60%）x=48这样的方程，注意引导分析数量关系：粮食总吨数×（1-60%）=剩下的吨数。

通过比较这几种方程，学生发现列x-60%x=48这种方程的人数最多，进而引发学生思考，这样的方程和其他的方程有什么区别？它有什么特点？学生通过比较发现：因为x-60%x=48方便，还有的学生认为这样的方程好解，也有的学生认为等号左边表示的粮食总吨数和已运走的吨数都是未知量，等号的右边表示剩下的吨数是已知量。培养学生仔细观察，对这样的方程进行优化，符合小学生的认知特点，这是小学阶段列方程解决实际问题的重点，也是难点。

三、学会评价与反思数学问题

建构主义学习观认为：一切知识最终都必须通过主体的建构活动才能得以完成，学习不是被动地接受，不是单纯地复制与同化，它要求学生在活动中進行建构，要求学生对自己的活动过程不断地进行反省、概括和抽象。学生学会评价与反思是学习过程的重要一环。

如上面《列方程解决稍复杂的百分数实际问题1》的教学，在分析解决问题后，引导检验反思，让学生理解把未知量放在等号的一边，已知量放在等号的另一边。学生会对已有的3个数量关系式进行筛选：粮食总吨数-运走的吨数=剩下的吨数。让学生自己选择合适的数量关系式，列出方程并解方程，找到正确的答案。最后再进行检验反思。如图2所示可以用120-120×60%来检验，看结果是不是等于48吨。也可以用（120-48）÷120来检验，看结果是不是等于60%……解完题之后回过头来对解题结果与过程进行回顾、反思、评价，是一种对自己解题活动过程的再认识。通过这样的检验反思，可使学生在解题活动中获得具有较大迁移价值的新的知识与经验，这有助于学生形成解决实际问题的策略，提高学生的解题能力。

又如“探索规律”的教学，教材呈现了“回顾反思”的场景，提醒教学进行这样的活动，启发学生说出有意义的想法。进一步清晰所发现的规律，丰富个体的数学知识；再认探索规律的过程中，积累开展数学活动的方法与经验；体验探索规律能促进思维能力的提升，增强对数学和数学学习的积极情感态度。学生回顾反思，一般围绕这些问题进行：研究了什么现象（问题）？得到什么结论？你能表达发现的规律吗？分几步来研究的？每一步研究什么？开展了哪些活动？哪些活动最有效？探索活动中应注意什么？对探索规律的活动还有什么想法？在探索规律过程中遇到什么困难？是怎样克服困难的？还有哪些收获？……

再如“解决问题策略”的教学，教材编排“回顾与反思”环节，主要包括三个方面的具体内容：一是对解决某一个问题过程的回顾与反思，侧重引导学生体会蕴含在具体解题过程中的方法和策略；二是对解决不同问题过程的回顾与反思，侧重引导学生通过比较深入体会不同解题过程在策略与方法层面的内在一致性；三是对以前学习中应用相关策略解决问题过程的回顾与反思，侧重引导学生联系已有的解题经验体会相关策略应用的广泛性。

综上所述，问题解决是一个错综复杂的整体思维建构，学生从数学的角度发现与提出问题、分析与解决问题，并适时引导学生评价与反思的过程，是一个有机融合的整体，不能截然分开，本文为了阐述的方便人为的“割裂”进行剖析。期望我们小学数学老师能继续对小学生数学问题解决做本真探讨！

【参考文献】

[1]义务教育数学课程标准[J].北京师范大学出版社，2012（4）.

[2]李晓梅.关于提高小学生问题解决能力的思考[J].课程·教材·教法，2011（12）.endprint