应用题教学要教会学生分析数量关系

李千锐

(广西桂平市罗播一中537213）

在我国小学一至六年级的数学教科书中，应用题教学是个重要的内容，各册数学教学科书中除了编排有恰当的应用题例题外，还编排了许多与应用题例题相应的应用题练习题供学生练习。按理说学生学习应用题的成绩是好的。但是笔者看到的最近几年小学毕业生会考的数学科答卷中，应用题的失分是最严重的。在一个班学生中，往往应用题得满分的是少数学生，甚至没有得满分的，有很多学生得半分以下，有些班级得半分以下的学生有五、六成，或更多一些。应用题的失分为什么这样严重呢？看来原因是多种多样的。其中带普遍性的原因就是学生没有掌握好解应用题的方法，不会分析应用题中的数量关系。解答应用题的关键就是在于能正确地分析应用题的数量关系。所以，我们的数学老师在应用题的教学中要教会学生分析数量关系。

1.分析应用题的数量关系，常用的方法有综合法和分析法

1.1综合法

这是个执因索果的分析方法，它是从题目的已知条件出发，根据数量关系，先考虑选择两个已知数量，作为一道一步应用题的已知条件，然后考虑求出其得数；把所求出的得数作为新的已知条件，与一个已知条件搭配，再作为另一道一步应用题的已知条件，求出其得数。这样逐步顺着推导直到求出应用题所求的得数为止。

1.2分析法

这是由果导因的分析方法，它是从题目要求的得数出发，根据数量关系，考虑要求这个得数需要知道哪两个条件；然后考虑把其中一个（或两个）需要知道但又是未知条件作为新的要求的得数，再找要求这一个（或两个）要求的得数所需要的条件；这样逐步逆推，直到所需要的条件在题目里都是已知数为止。

例、一个化肥厂要生产10800吨化肥，原计划25天完成，实际每天比原计划多生产108吨，实际用多少天完成任务？

1.用综合法分析

（1）知道要生产的总吨数（10800吨）和原计划用的天数（25天），能求出什么得数（能求出原计划每天生产的吨数）。

即：总生产的吨数（10800吨）÷原计划天数（25天）＝原计划每天生产的吨数。（第一道一步应用题）

（2）知道原计划每天生产的吨数和实际每天比原计划多生产的吨数（108吨），能求出什么得数？（能求出实际每天生产的吨数）

即：原计划生产吨数+实际每天比原计划多生产的吨数（108吨）＝实际每天生产的吨数。（第二道一步应用题）。

（3）知道了生产的总吨数10800吨和实际每天生产的吨数，能求出什么得数？（能求出生产的总吨数所需要的天数）。

即：总生产的吨数（10800吨）÷实际每天生产的吨数＝完成总生产吨数（10800吨），所用的天数。（第三道一步应用题）。

用综合法思路图表示是：

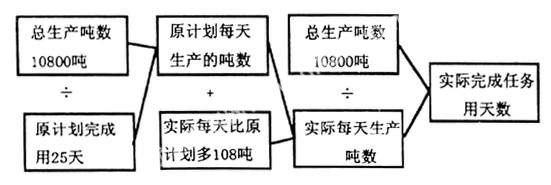
1.2用分析法分析

（1）要求出实际完成总生产吨数所用的天数，需要知道哪两个条件？（要知道总生产任务的吨数和实际每天生产的吨数这两个条件）

即：完成总生产吨数实际所用天数＝总生产吨数（10800吨）÷实际每天生产的吨数（未知）

（2）要求出实际每天生产的吨数，要知道哪两个条件？（要知道原计划每天生产的吨数和实际每天比原计划多生产的吨数，这两条件）。

即：实地每天生产的吨数＝原计划每天生产的吨数（未知）+实际每天比原计划多生产的吨数（108吨）

（3）要求出原计划每天生产的吨数，要知道哪两个条件？（要知道总生产的吨数和原计划完成任务的天数这两个条件。）

即原计划每天生产的吨数＝总生产的吨数（10800吨）÷原计划完成任务所用天数（25天）

用分析法思路图表示是：

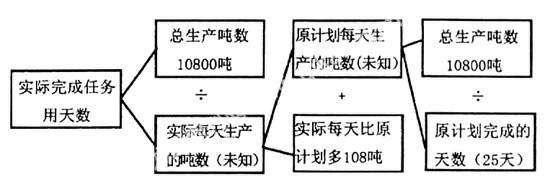
解：分析列式：

①原计划每天生产多少吨？

10800÷25＝432（吨）

②实际每天生产多少吨？

432+108＝540（吨）

③实际用多少天？

10800÷540＝20（天）列综合算式：

10800÷（10800÷25+108）

＝10800÷540

＝20（天）

答：实际用20天完成。

综合法和分析法的思考方法是相反的。但是在解答应用题时，常常是既从已知条件出发，考虑可以求出什么数量；又考虑要求题目的所求问题的得数，需要知道（或要求）什么条件。两种分析方法交替使用，解题才更为方便。

例：某学生在爬山锻炼中，上山下山共用了4小时，如果上山用2.4小时，下山的速度是每小时9千米，这个学生上山的速度是多少？

分析：交替使用分析法和综合法思路如下：

要求学生上山的速度（题目所求），需要知道了上山走的路程（未知条件）和上山所用的时间（已知条件）

上山的速度＝上山的路程÷2.4（分析法）

要求上山的路程，只需求出下山的路程。上山的路程＝下山的路程。

要求下山和路程，需要知道下山的速度（已知条件）和下山的时间（未知条件），下山的路程＝9×下山用的时间。（分析法）

已知他上山下山共用了4小时和上山用2.4小时，可以求出下山的时间。4-2.4＝下山用的时间。（综合法）

已知下山的速度（每小时9千米）和时间（1.6小时）可以求出下山的路程。9×（4-2.4）＝下山的路程（综合法）

解：综合算式是：9×（4-2.4）÷2.4

＝9×1.6÷2.4

＝6（千米）

答：这个学生的上山是每小时6千米。

为了便于理解题意和有助于进行分析，还可以用图或实物，实物图或线段表示条件和问题，帮助我们找到隐蔽的数量关系。

教会了学生分析应用题的数量关系，学生学习应用题的成绩就会得到提高。

收稿日期：2009-04-02