摭谈数学试卷讲评课的“四要”“四不要”

江苏省睢宁高级中学北校 武瑞雪 (邮编:221200)

摭谈数学试卷讲评课的“四要”“四不要”

江苏省睢宁高级中学北校 武瑞雪 (邮编:221200)

试卷讲评课是一种重要的课型,可帮助教师了解教情、学情,弥补教学不足;帮助学生巩固知识、强化技能、纠正错误、找出薄弱、规范答题、拓展思维、提升能力、总结规律和方法．现笔者结合自己的教学实践,摭谈有效数学试卷讲评课中应坚持的“四要”“四不要”．

1 数学试卷讲评课中的“四要”

1．1 要做好充分的课前准备

古人云:“工欲善其事、必先利其器”,要想将试卷讲评课上得高效扎实,师、生课前必须准备充分．

1．1．1 教师方面

(1)教师应先静心做卷(做完之前不要看参考答案)、认真批卷,必要时,还要面批部分学生的试卷．只有教师先思、先做,才能较好地应对、处理学生在试卷中出现的问题．

(2)统计班级平均分、及格率、优秀率、最高分、最低分、各分数段的人数等,留待课堂上公布,但不要公布分数较低的学生姓名、排名．

(3)统计典型试题的解法,对易错的题目,错因是什么,必须统计详细,留待课堂展示、剖析,同时,还要通过资料查找或教师自行编制类似题目,留待讲评课上练习使用．

1．1．2 学生方面

教师发下批改过的试卷后,应留给学生一定的时间,要求学生把那些做错的题目先自行纠错,把那些因时间不够而未做的题目独立做完．讲评前再将标准答案公布给学生,让学生进行第二次纠错,充分了解自己薄弱之处,以便在课堂上有目的、有针对性、有重点地听讲并记录,而不是被动地跟着教师抄解题过程．

1．2 要重视错误资源的利用

案例1已知a、b＞0,且4a＋b＝5,求的最小值．

这是我校一次《不等式》单元测试卷上的一道题目,笔者听了教师A的试卷讲评课,感触颇深．教师A课前收集来自学生的共7种解法,其中有正确的,也有错误的,并全部打印出来,发给学生,让学生先自行判断哪些解法正确?哪些解法错误?错因又是什么?

方法1因为a、b＞0,4a＋b＝5,所以10＝

当且仅当4(a＋1)＝b＋1时取等号,

当且仅当a＋1＝b＋1时取等号,

方法2因为4a＋b＝5,所以4(a＋1)＋(b＋1)＝10,所以

方法3因为a、b＞0,所以4(a＋1)＋

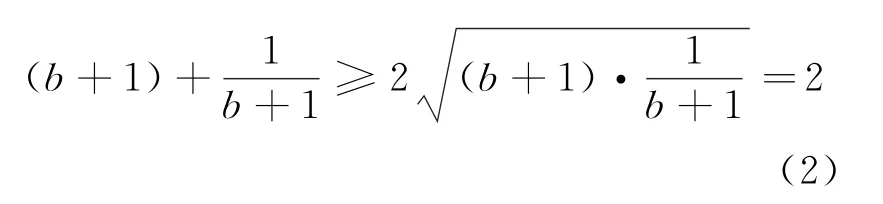
又4a＋b＝5,所以4(a＋1)＋(b＋1)＝10,

方法4因为a、b＞0,所以

当且仅当a＋1＝b＋1,即a＝b时取等号,

又因4a＋b＝5,所以4a＋a＝5,所以a＝b＝1,所以,所以的最小值为1．

方法5因为4a＋b＝5,所以4(a＋1)＋(b＋1)＝10,又a、b＞0,所以

方法6因为a、b＞0,4a＋b＝5,所以

方法7因为a、b＞0,4a＋b＝5,所以b＝5

则

点评由于学生在课前进行了充分的思考、讨论,对错题先行纠错,所以课堂上学生发言积极、踊跃,通过讨论,最后由生1总结．

生1:前4种方法都是错误的,错因如下:方法1、2、3都错在两次使用均值不等式时,其中等号不能同时成立,等号无法传递下去．事实上,在方法1、2中,当两等号同时成立时,应有4(a＋1)＝b＋1,且a＋1＝b＋1,则得a＝b＝－1,这与已知矛盾;方法3中,当两等号同时成立时,应有,且,即或,且b＝0或－2,这与已知矛盾;方法4错在用均值不等式求最值时,忽略了三个条件“一正二定三相等”中的第二个条件——求和的最小值时,积应为定值,在式子中,不是定值．

方法5、6、7都是正确的．方法5是“整体1代入法”;方法6是“消元法”、“均值不等式法”;方法7是“消元法”、“导数法”．方法5最简捷,方法6及方法7虽是通法,但稍显麻烦．

点评生1所“讲”的,不是由教师直接“告知”的,而是由学生课前独立思考、相互讨论,“悟”出来的,在这个过程中,学生的思维得到了充分的锻炼,能力得到了应有的提升．

生2:(教师引导生2归纳)利用均值不等式的两个注意点:

(1)两次使用均值不等式时,等号必须能同时成立;

(2)使用均值不等式求最值时,一定要满足“一正二定三相等”．

为了解学生掌握情况,教师A又给了一道变式题:已知a、b＞0,且a＋b＝1,求的最大值．答案:

并当堂给了3道检测题:

2．函数y＝loga(x＋2)－3(a＞0,a≠1)的图象恒过定点P,而点P在直线l:2mx＋ny＋1＝0上,其中mn＞0,求的最小值．答案:

检测结果表明效果很好!

后记(1)爱迪生说过:“失败也是我需要的,它和成功对我来说一样有价值,只有我知道一切做不好的方法之后,我才知道做好一件工作的方法是什么．”对错误率较高的试题,只有将错因剖析透彻,才能有利于消除“老错误重犯”现象．

(2)只有让学生亲历由“误”到“悟”的过程,试卷讲评课才能高效,才能引起学生共鸣和积极的配合．

(3)要避免大容量、快节奏,要给学生足够多的思考、探究、琢磨的时间,哪怕一堂课只讲一、两道试题,只要讲足讲透,有时也是值得的,甚至是高效的．

1．3 要借题发挥

案例2如图1,设四边形ABCD为平行四边形若 点 E、F 满 足,则的值为______．

图1

分析此题宜用基底法、坐标法,不宜用定义法．_

解法_1(基底法)选为基底,过程略．答案:0．

解法2(特殊值法)

由于是填空题,不妨设平行四边形ABCD为矩形,建立如图2的直角坐标系(过程略)．

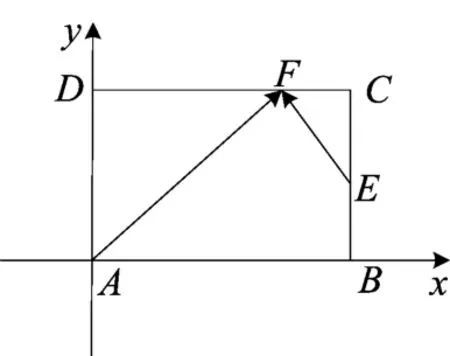
图2

变式如图_3,四边形ABCD为平行四_边形,＝2,则的值为______．答案:22．

分析此题宜用基底法、坐标法,不宜用定义法．

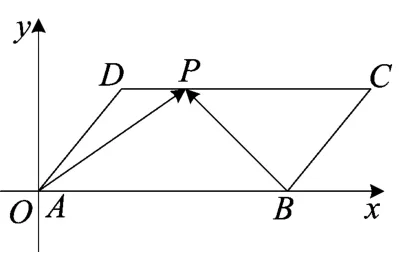
图3

此题也可设 ∠PAB＝α,则D(5cosa,5sina),则P(5cosa＋2,5sina),…)．

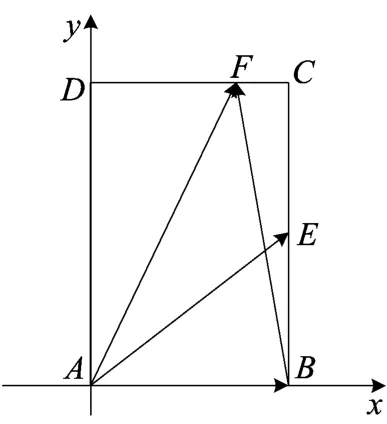
图4

课后矫正补偿练习:(2012年江苏卷)如图4,在矩形ABCD中,AB＝2,BC＝2,点E为BC的中点,点F在边CD上,若,则的值为______．

分析通过分析,此题宜用坐标法．答案为 2．

对试卷中内涵丰富或出错率较高的试题“借题发挥”:一题多法,一题多变,并及时进行课后矫正补偿练习等,利于学生跳出题海、减轻负担,利于优化学生的思维品质．另外,每隔一段时间,教师要根据平时记录下的学生易错易混题,专门编制一套试卷,以强化巩固．

1．4 要归类讲评

教学实践证明,若将一份试卷上的试题归类(如按方法、知识点、错误类型等分类)讲评,效果会更好,如,在一份《平面解析几何初步》单元测试卷上,有“曲线恒过定点”两道题及“易因忽视特殊情况致错”的两道题,可分别放一起讲评:

案例3(1)对任意k∈R,直线(2＋a)x＋(3a－4)y＋2a－1＝0(a∈R)恒过定点______．

(2)已知直线l:y＝k(x－4)＋2(k∈R),圆C:x2＋y2－10x－6y＋30＝0,则直线l与圆C的位置关系为( )

A．相交 B．相切

C．相切或相交 D．相切、相交或相离

案例4(1)求经过点A(5,2),且在x轴上的截距等于在y轴上截距2倍的直线方程．

(2)从圆 (x－3)2＋(y－2)2＝1外一点P(4,5)向这个圆引切线,求切线的方程．

2 数学试卷讲评课中的“四不要”

2．1 不要主次不分

不要主次不分,不要“对答案”式地逐题讲解、面面俱到,否则,会让学生生厌,且也是低效的．要严格遵循“三讲三不讲”的原则——讲重点、讲难点、讲易错点;不讲学生已经会的、不讲学生自己能学会的、不讲那些讲了学生仍然不会的．

当然,对于那些难度过大的题目在课堂上不讲,但是在课后,要对学有余力的数学“尖子生”进行个别辅导,这样做,既可防止课堂教学时间的隐性流失,又可使数学“尖子生”能够“吃得饱”．另外,如果有一些学生在课堂上有个别题目未听懂,或有一些学生自己不会做的题目教师没选讲到,或个别学生所犯的特殊性错误等,可在课后进行个别辅导,应杜绝“一人生病,众人吃药”的现象．

2．2 不要就题论题

有些教师讲完一道题,就想立刻讲解下一道题,不变式拓展,怕耽误时间,认为一堂课讲完一张试卷就是高效的,这些教师还常抱怨“为什么我讲过这类题目,当时学生也是听懂了的,现在再考学生又不会了呢?”殊不知,“就题论题”式的教学方法虽然简单省事,却是效率低下的,所讲评的知识方法难以扎根学生心中,而“就题论法”可以让学生“跳出题海”,加深学生对基础知识、基本方法的理解和掌握,利于消除“学生课上听得懂,课下不会做题”的“懂而不会”现象,从而切实提高数学教学的效益和质量．

2．3 不要越俎代庖

试卷讲评课,应充分发挥学生的主体作用,思路和解法让学生“讲出来”,对于那些重要的、典型的题目,其解题过程要让学生“板演出来”,充分暴露学生的思维过程,然后由学生讨论其正误、优劣,尽最大可能调动学生参与的积极性,教师不要“越俎代庖”,更不能搞“一言堂”,当然,对于较难的题目,教师恰当的点拨、指导还是必要的．

2．4 不要忽视考试技巧的指导

不少学生,平时学习很认真,基础知识很扎实,基本技能也很熟练,就是在大型考试中,考不出好成绩,很是遗憾．所以在数学讲评课中,不要忽视考试技巧的指导:拿到试卷,应通览全卷,确定易做、一般、困难分别是哪些题,先解题型熟悉易做的题,最后做那些题型生疏、不易做的题,并养成“审题慢,解题快”的习惯．

2017-07-26)

江苏省中小学教学研究第十一期重点课题《数学有效教学行为的研究——数学学习中懂而不会现象的研究》的阶段性成果,课题编号:2015JK11-Z024．