基于“三个理解”的情境引入研究——兼谈参加优质课评比的几点感悟

安徽省铜陵市第一中学 陈恩兵 (邮编:244000)

基于“三个理解”的情境引入研究
——兼谈参加优质课评比的几点感悟

安徽省铜陵市第一中学 陈恩兵 (邮编:244000)

2016年12月笔者参加了第八届全国高中青年数学教师优秀课评比与研讨活动,并荣获一等奖．本文是笔者2年来先后通过市、省级选拔并参加国赛的几点感悟,通过对情境引入环节的解读与案例展示,希望对有志于参加优质课评比的年轻教师有所帮助．

1 对“三个理解”的解读是上好一节优质课的前提

1．1 理解数学

新课标指出要“了解数学知识的背景,准确把握数学知识的逻辑意义,深刻领悟数学知识反映的思想方法,把握知识之间的多元联系,挖掘其蕴含的科学方法、理性精神和价值观资源”,是精确设置教学目标和方法的保障．

理解数学可以从三个方面着手:一是深刻领悟数学知识的本质和内涵,这决定了一节课的高度．教学活动的设计和展开,教学问题的预设和生成都离不开教师对所教内容本质的领悟．二是对数学知识所蕴含的思想和方法的理解,这是我们的教学活动能否驱动学生思维,促进高效课堂的关键．三是建构研究的路径和基本过程,这是实现教学目标的有效手段．

1．2 理解学生

学生是获得数学知识的主体,新课标指出“了解学生已有的学习基础、学习经验、学习心理、思维特点等等,这样才能立足于学生的最近发展区,开展教学活动”．理解学生是教学方法设计,重难点设计的依据,是问题设计的关键．

一是要准确把握学生的客观现实和数学现实即认知基础,这是设计教学活动的基础．学生的思维活动的载体包括逻辑推理、代数运算、几何直观、数形结合．要想立足于学生的最近发展区,既不能让学生随口而答,又不能让学生怎么努力也够不着,那么必须从思维活动的载体出发进行学情分析．二是要了解学生的学习习惯、问题和疑问,只有这样才能预设能够驱动学生思维、反映数学本质的问题．

1．3 理解教学

理解教学就是以课程标准为依据、以核心素养为方向,以数学知识为主线,学生在原有的知识经验的基础上主动建构的过程;学生是学习的主体,教师是学习的引导者和合作者．在教学过程中要注重预设与生成的关系,预设是为了更好的生成,生成要揭示数学本质、渗透数学思想方法．

由于应试教育的影响,在传统课堂教学中普遍存在三个弊端:一是教师讲得多;二是学生“参与少”,课堂教学实践环节薄弱;三是教师“目中无人”,缺乏民主,过分强调教师的主导作用,忽略课堂教学过程中学生的主体参与地位．以上弊端造成学生依赖性过大,自信心不足,没有提出问题发现问题的心态,缺乏创新的意识和能力,厌学情绪明显,学习效率不高．

建构主义学习观认为:学习意义的获得,是每个学习者以自己原有的知识经验为基础,对新信息重新认识和编码,建构自己的理解．教学是师生双边活动的一致和统一,现代教学理论早已阐明,在教学双边活动中教师是引导者、学生是学习的主体,美国教育家苏娜丹戴克有句名言:“告诉我,我会忘记,做给我看,我会记住,让我参与,我就会完全理解”．布鲁纳指出:我们教一门科目,并不是希望学生成为该科目的一个小型图书馆,而是要他们参与获取知识的过程．学习是一种过程,而不是一种结果．这一过程的成功与否,关键在于教师是否能交给学生恰当的自主权和能动的探索空间．

教师要把以“教”为重心逐渐转移到以“学”为重心,把以“研究教法”为重心逐渐转移到以“研究学法”为重心,并做好教与学的最佳结合．以“学”为重心,其基本精神就是使学生爱学习,学会学习,养成良好的学习习惯．叶圣陶先生说:“教是为了不需要教．”面对21世纪对人才的需求,“授人之渔”已成为师者的最高教育境界．

2 情境引入——创设有效情境，促进高效教学

知识是人类从实践活动中得来的,是对实际事物及其运动和变化发展规律的反映．这也就是说,知识本身是具有丰富生动的实际内容,而表征它的语言文字(包括符号图表)则是抽象和简约的,学生所学的正是语言文字所汇集成的书本知识即教材．教学情境就是以直观方式再现书本知识所表征的实际事物或者实际事物的相关背景．显然,教学情境解决的是学生认识过程中的形象与抽象、实际与理论、感性与理性以及旧知与新知的关系和矛盾．捷克教育家夸美纽斯曾说:“一切知识都是从感官开始的”．

奥苏伯尔的有意义学习理论认为:创设一定的“问题情境”,能够使学生对知识本身产生兴趣,进而产生认识需要,产生一种要学习的倾向,从而能够激发学习的动力．教师应在教学过程中创设以问题为核心的教学情境,促使学生在知识与情感的相互作用下参与整个教学过程,激发学习数学的兴趣,启迪学生的思维,引导学生深入探究,指导学生主动构建．

创设体现数学知识发生、发展过程,体现数学知识与实际生活紧密联系的问题情境,可以从三个方面入手:一是从实际背景、生活引入,体现数学知识产生的迫切性和必要性;二是从数学知识的发生、发展过程引入,让学生体会数学知识的来源、本质及地位;三是从学生已有的知识结构引入,目的是形成强烈的认知冲突,激发学生学习的热情．

案例1射影选址问题(笔者2015年参加安徽省优质课课例并获一等奖)

师:我们有了点和线段的射影的概念,下面我们一起来看一个实际问题．(教师展示问题情境,并在黑板上作图)

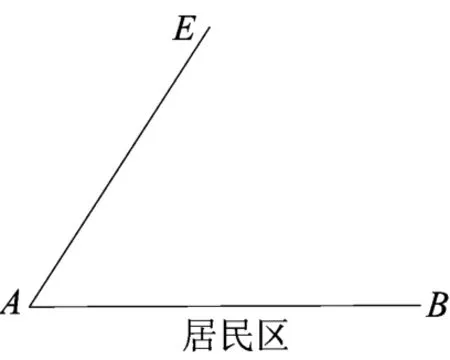
师:如图,某化工厂在B处有一仓库,现拟在路线AE上修建一分厂C．

(1)为使仓库到分厂C的路程最短,分厂C应建在何处?

生1:过B作AE的垂线

师:分厂C建在……?

生1:垂足C处．

师:非常好!C就是B在……

生:(齐声)直线AE上的射影．

(教师在黑板上作出垂线BC)

师:这类问题我们称之为射影选址问题．请大家接着思考第二个问题．

(2)已知离C的距离越近,空气污染指数越高．环保部门要在AB上建立污染监测站D,实时监测该分厂的最大污染指数,那么监测站D应建在何处?

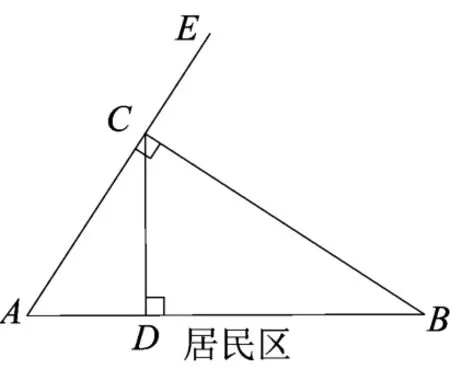
生2:过C做AB的垂线,垂足D就是监测站所建位置．

师:(教师在黑板上作出垂线CD)很好!D是谁的射影?

生2:C．

师:在哪条直线上的射影?

生2:D是C在直线AB上的射影．

师:很好!请坐．这一类问题在生活中比较常见,我们可以利用射影的概念加以解决．下面请大家接着思考第三个问题．

(3)若已知BC和AB,那么你能求出BD吗?

(学生独立作图,思考)

《课程标准》指出:数学来源于生活,又应用于生活,与学生的生活经验存在着密切的联系．几何学起源于土地测量问题,直角三角形在几何度量中有着重要的地位．通过情境2的创设,既让学生体会几何来源于生活,是有用的,又让学生体会直角三角形的特殊性．情境2本身来源于生活,有很强的现实性和趣味性,在教师叙述结束后学生的思维将会彻底激活,课堂上气氛一定会更加热烈,引人入胜;同学们一定会表现得跃跃欲试,很想一探究竟．

一个好的情境,能够充分调动学生的原有生活经验和数学背景,更能激起由情境引起的几何意义的思考,从而让学生有机会经历“问题情境—建立模型—解释和应用”这一重要的数学活动过程．

几何在工程测量等领域都有着重要的应用,但如何通过实例引入2次垂线,让学生体会学习射影定理的必要性从而认识到学习几何、学习数学是有用的,一度困扰了笔者．为此,笔者查阅了非常多的资料,最终灵感来源于航海中的追及问题及噪音污染问题．案例1紧紧围绕射影定理的主图,将最短路程与最大空气污染指数纳入背景,这些都是学生熟悉的实际问题．我将情境2分解为3问,让学生的思维层层递进,一步步由生活走向几何,完整经历生活——几何的抽象过程．

案例2从几何研究的一般过程、方法引入直角三角形的射影定理

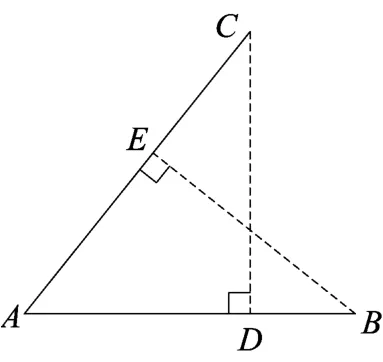
师:如图,AC和其射影的长度大小关系如何?

生:AC＞AD．

师:图中是否存在等量关系呢?

生:发现相似,得出比例式．

师:当C在运动时,这些关系还变化吗?特别的,运动到E点呢?

章建跃博士指出帮助学生掌握进一步学习所必需的数学知识、技能、思想和方法是“立德树人”目标的基本内涵之一．这就要求教师在传授基本知识、基本技能的同时,促进学生思维能力和创新意识的发展．笔者认为以知识为载体,让学生学会处理问题的思想和方法并形成基本活动经验是落实核心素养的主要抓手．

平面几何研究的主要对象是点、线的位置、大小、形状,往往采用定性要定量计算、一般到特殊等思想和方法,而观察运动中的不变性往往是发现几何性质和规律的主要手段．案例2的设计正是体现了几何学研究的一般过程、思想和方法,案例2通过问题将几何的研究对象直接呈现在学生面前,并引导学生从运动的角度观察图形,在此过程中,学生就能掌握学习几何到底要研究什么,怎么去研究,需要采取什么样的方法和思想,从而也就获得了处理新问题的能力即思维、实践和创新能力．

案例3平改坡(2016年参加全国优质课评比课例并获一等奖)

为了美化城市,许多城市实施“景观工程”,对现有平顶房进行“平改坡”,将平顶改为尖顶．

师:如图1,这里有线面平行关系吗?

图1

图2

学生(齐声):EF//面ABCD．

师:正是由于EF//面ABCD,屋顶才显得美观．若是如图2(拖动EF),那就太难看了!

师:那么,你觉得可以提出一个什么问题?

学生:如何确保EF平行平面ABCD?

师:即在数学上,我们……

学生:如何判定线面平行?

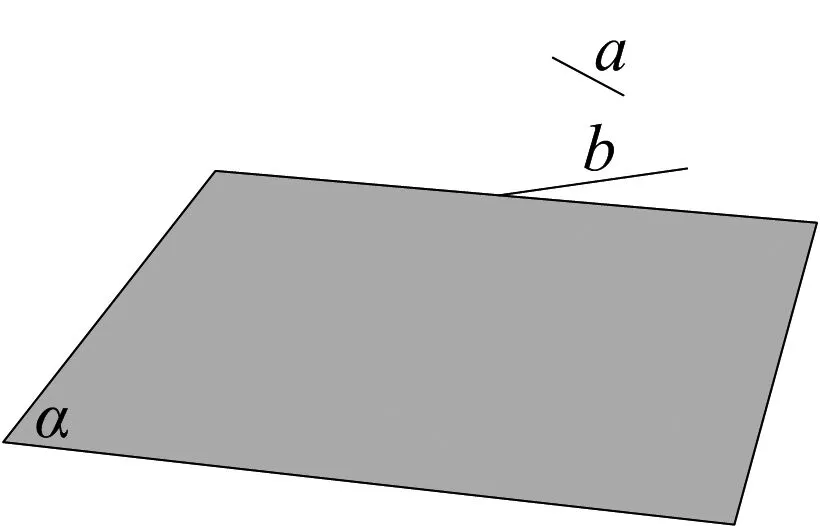
图3

师:请同学们观察图3中直线与平面的位置关系．

学生(争论不休,无法给出平行与否的原因)

师:如何判定线面平行呢?直观感觉可靠吗?定义可行吗?

新课标指出:数学源于对现实的抽象,基于抽象结构,通过符号运算、形式推理、模型构建等理解和表达事物的本质、关系和规律．让学生学会用数学的眼光观察世界,会用数学思维思考世界,会用数学语言表达世界是课堂教学的主要任务．培养学生问题意识和问题发现能力是课堂教学的首要目标．通过实例发现并提出现实问题,并抽象出能反映数学本质的数学问题有着非凡的价值．案例2通过景观工程让学生抽象出具有数学美的几何图形1以及不具备平行性质的几何图形2并形成强烈的冲突,让学生发现问题、提出问题成为可能．

在判定定理的引入上,也没有平铺直叙,而是通过一个似是而非的情境(图3)让学生理解直观感知不可靠,定义未必可行,从而激发学生的兴趣,使得判定定理的引入更加迫切和自然．

1 中华人民共和国教育部．普通高中数学课程标准(实验)[M]．北京:人民教育出版社,2007

2 缪林．基于“三个理解”的“求曲线方程”教学设计[J]．中数参,2016(11):18-20

2017-06-26)