“有序化”解题思路探索
——以一道动态综合题为例
陆腾宇
(江苏省常熟市昆承中学)
“有序化”解题思路探索
——以一道动态综合题为例
陆腾宇
(江苏省常熟市昆承中学)
几何动态综合问题信息量大,图形复杂,灵活性强,能比较全面地考查学生知识综合运用的能力,备受命题者的青睐.学生在解此类问题时,往往受到智力发展水平、解题经验欠缺等因素的影响而无从入手,因此需要把探求解题思路的过程程序化,以期学生在模仿中提高分析、解决问题的能力.
动态问题;解题思路;有序化
动态几何问题,即随着图形中的某些元素(点、线、形等)的运动变化,导致图形之间的空间形式、数量关系发生变化,从而使结论或者改变、或者保持不变的几何问题.这类问题对学生分析问题的能力,图形的想象力,动态思维能力的培养和提高有着积极的促进作用.但这类问题文字叙述繁杂,条件隐蔽,加之图形复杂,学生普遍感觉无从着手.本文拟对七年级上学期期末数学试卷中的一道动态问题进行剖析,遵循波利亚的解题表,介绍寻找解题思路的一般化方法,以期提高七年级学生解题的有序化思维.
题目如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方.将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.若射线OC的位置保持不变,且∠COE=140°.
(1)则当旋转时间t=______秒时,边AB所在的直线与OC平行?
(2)如图2,在旋转的过程中,是否存在某个时刻,使得射线OA,OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在,求出所有满足题意的t的取值;若不存在,说明理由.
(3)在旋转的过程中,当边AB与直线DE相交时(如图3),求∠AOC-∠BOE的值.

图1
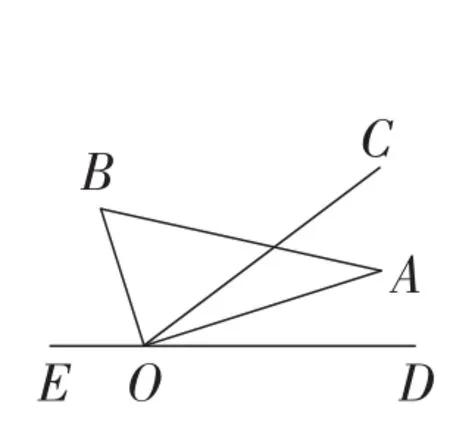
图2
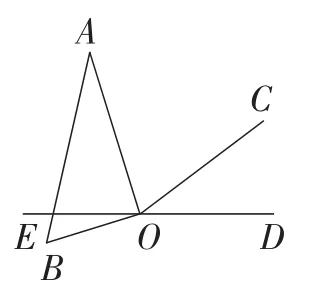
图3
解题过程按如下四步实施.
一、弄清问题
题干的条件有如下几点.
条件1:过直线DE上一点O在直线DE上方作射线OC,且该射线位置不变,∠COE=140°;
条件2:将一直角三角板AOB(∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方;
条件3:将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,旋转时间为t秒.三角形的旋转解读为三角形边的旋转.例如,边OA绕点O按每秒10°的速度逆时针旋转,这样旋转角度为射线OA扫过的角度.
题干追加的条件有如下几点.
第(1)小题追加条件4:直线AB∥OC;
第(2)小题追加条件5:在旋转的过程中,射线OA,OC与OD中的某一条射线是另两条射线所夹角的平分线;
第(3)小题追加条件6:边AB与直线DE相交(如图3).
二、拟定计划
1.画出图形
问题1:用手头的三角板按要求旋转(动手操作是发现动态问题中图形特殊位置的有效途径),发现满足AB∥OC的两种特殊位置,分别画出如图4、图5所示的图形.

图4

图5
问题2:分三种情况:①OA是角平分线;②OC是角平分线;③OD是角平分线.画出如图6~8所示的图形.

图6

图7

图8
问题3:分别用数量来表示∠AOC和∠BOE的大小.
2.类比联想
以前见过类似的问题吗?是否知道一个用得上的定理?是否知道一个与该问题相关且早已解决的问题?如何回到定义中去?能否用数据来描述未知量?
问题1中可用的定理是:两直线平行,内错角相等(或同旁内角互补),于是图4中有∠AOC=∠A=30°,图5中有 ∠BOC=∠B=60°或 ∠A+∠AOC=180°.直观感知t的变化改变旋转的角度,所以用含t的代数式表示旋转角度,即∠DOA=10t°.
问题2回到角平分线的定义,于是图6中有∠DOA=∠AOC,图7中有 ∠DOC=∠AOC,图8中有∠AOD=∠DOC(此时∠DOA并不表示旋转角度);图6、图7中的∠DOA=10t°,而图8中的∠DOA=(360-10t)°.
问题3中的 ∠AOC=∠AOD-∠DOC=(10t-40)°,而且∠BOE=∠DOA+∠AOB-∠DOE=(90+10t)°-180°=(10t-90)°.
至此,问题中的变“形”都用变“量”来描述,实现了角度的“动态”转化为数量的相对“静态”,初步体现了由形到数的转化.
三、实现计划
为求t的值,构造一个关于t的方程是不错的想法.这需要找到问题的相等关系,这个相等关系可以是对同一个对象算两次,也可以是两个等量的关联.
问题1中的两种情况都是对旋转角度算两次.
图4中有∠DOA=∠DOC+∠AOC,于是10t=40+30,解得t=7.
图5中∠DOA=360°-∠AOD,现在关键求∠AOD的值.由AB∥OC,得∠A+∠AOC=180°.因为∠A=30°,所以 ∠AOC=150°. 又因为 ∠COD=40°,所以∠AOD=110°.所以10t=360-110.解得t=25.
综上所述,t=7或t=25时,AB∥OC.
问题2由角平分线提供的两个相等的角构造方程.
图8中有∠DOA=∠DOC,于是360-10t=40,解得t=32.
综上所述,t的值为2,8,32.
问题3有 ∠AOC-∠BOE=(10t-40)°-(10t-90)°=50°.
四、反思
1.能否优化某些问题的求解过程
图5解法的再思考.
方法1:图5中∠AOC=150°,∠COE=140°,
而∠COE+∠AOC+∠AOE=360°,
因此,∠AOE的大小是关键.
容易看出∠AOE是旋转角度减去一个平角∠DOE,
所以∠AOE=(10t-180)°.
于是140+150+(10t-180)=360.
解得t=25.
方法2:由AB∥OC,得∠BOC=∠B=60°.
又因为∠COD=40°,
所以∠BOD=20°.
所以∠AOD=∠AOB+∠BOD=90°+20°=110°.
所以旋转的角度10t=250°.
解得t=25.
2.解题思路的探索“有序化”是七年级学生内在的需要
解题方法浩如烟海,方法、技巧各有优势.对七年级学生而言,尝试探索解题思路的一般化方法,既尊重学生的智力发展水平,又养成良好的有序思维的习惯.高手解题无招胜有招,但功力臻化境前都是从苦练招式开始的.因此,归纳解题的一般步骤是十分必要的.
首先,需要弄清问题.知道已知条件是什么?要求的是什么?满足条件是否可能?已知和未知之间的逻辑关系能否链接?能否有意识地把条件分开?需要引入什么符号?等等.
其次,拟定解题计划,画出符合题意的图形.能否用“变量”来描述“变形”,实现“数”“形”之间的有效转化,能否把问题转化为熟悉的问题(或早已解决的问题),实现解题方法的“转化”.
再次,能否找到一个有用的等量关系,构造一个方程?需要完成哪些计算?
最后,反思解题方法,能否用不同的方法解决问题?能否把问题结果或解题方法应用到其他类似的问题中?
3.数形结合是解动态问题的一般思想
(1)不管图形怎么变化,设法用“变量”控制“变形”,即用代数式表示“变形”,实现由动到静的转化;
(2)围绕数量关系构造方程,实现由形到数的转化.
解题时不妨多思考以上的问题,或许会对学生的解题能力的提高有帮助.
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2] G.Polya.How to Solve It:A New Aspect of Mathematical Methoel[M]. 阎育苏,译.北京:科学出版社,1982.
2017—07—05
陆腾宇(1969—),男,中学高级教师,主要从事课堂教育和解题研究.

