微课助力中考数学小专题复习
——以微课“特殊的相似:一线三等角”为例
康 丽
(天津市小站实验中学)
微课助力中考数学小专题复习
——以微课“特殊的相似:一线三等角”为例
康 丽
(天津市小站实验中学)
在微博、微信迅速发展的“微时代”,教育界也开启了一种新的教学方式——微课.文章以微课“特殊的相似:一线三等角”为例,科学、合理地设计了教学过程,并结合近几年天津市中考试题,为深入理解并掌握“一线三等角”模型搭建平台,在此基础上简述了微课的创作及使用说明,以期为中考数学小专题复习提供借鉴.
微课;中考数学;小专题复习;一线三等角

微信扫描二维码线上观看本文配套微课
中考数学复习是整合知识、提升认知的系统工程,教师必须从整体出发,把初中所有的知识点分成若干个专题进行复习,从知识、技能、方法等方面展开,横向、纵向加以研究,既要使知识有一个“基本点”(基本图形),又要使知识有一个“生长点”(变式),对知识进行再归纳、再总结,深入理解知识间的关系,促进学生建立系统的数学知识体系,促进学生有效复习,提升学生课堂效率.但中考复习内容多、难度大,因此将若干个大专题分解成小专题势在必行,而且要尽量做到专题虽小,但知识不小;内容虽少,但延伸不断.
鉴于小专题的特点,为达到高效复习的目的,可以借助微课进行小专题复习.一节微课只讲解一两个知识点,看似很慢,但稳步推进,效果显著,而且微课适合学习程度不同的学生,视频播放快慢可以调节,让不同的学生根据自己的基础水平和接受程度控制视频的快慢.另外视频可以反复播放,使那些平时反应慢的又羞于发问的学生能够反复观看,主动研究,最终达到小专题复习的高效吸收,促进高效课堂的构建.
笔者近几年也在不断尝试借助微课进行中考小专题复习,本文以微课“特殊的相似:一线三等角”为例,谈一谈笔者的思考.
一、微课“特殊的相似:一线三等角”
1.“一线三等角”模型
一线三等角是一种特殊的相似关系,也是初中重要的几何基本模型(如图1).

图1
它指的是当某条直线或线段的同一侧有依次排序的三个相等的角(∠C=∠BAD=∠E)时,首尾两个角所在的三角形相似,即△ABC相似于△ADE,这种特殊的相似称为“一线三等角”.它是初中重要的几何基本模型,通过相似的比例关系建立方程或函数来表示数量之间的变化关系,以期来求解问题,是解决中考几何问题的重要工具.而从复杂图形中分离出“一线三等角”模型是“一线三等角”的重点,亦是难点.
2.适用对象
“一线三等角”既适用于九年级下学期刚学相似的学生,促进学生初步对一线三等角的理解,又适用于对中考几何题有一定解决能力并有待提升综合能力的学生,弥补和改善学生漏听或未听懂这部分知识的不足,旨在促进学生深入理解方法和思想,从复杂图形中分离出基本数学模型,对解决问题有化繁为简的效果.
3.教学分析
(1)教学内容.
“一线三等角”的本质是一个重要的几何基本模型,数学模型是对客观事物的空间形式和数量关系的表现形式,初中阶段的“一线三等角”模型是利用方程或函数等来表示数量之间的关系或变化规律.此类问题的核心思想就是模型思想,关键的解题途径是能从复杂图形中分离出此模型,把握基本图形并建立方程或函数.
(2)教学方法.
本节专题复习课按照从特殊到一般的方法探索“一线三等角”,经历观察、实验、归纳、推理、验证的过程,掌握“一线三等角”证明的过程,让学生掌握基本图形,渗透类比思想和模型思想,利用中考试题进行巩固训练,最后对模型进行变式、反思和升华.
(3)学习方式.
以微课的形式呈现,有两种学习方式:学生自己在家观看视频时,可随时暂停,先独立思考,再听分析和解答,并规范解题步骤,把未听懂的、勉强懂得的、认为还可以再深入的问题记录在本子上,准备在课堂上与其他学生讨论;集体观看视频时,可以先观看,独立思考,再与同伴或老师进行交流.
4.教学过程
(1)勾股导入,发现问题.
导入:回顾勾股定理的一种证明方法(如图2),可知任意两个相邻的直角三角形是全等的,这个图形是八年级全等一章常见的基本图形,那么如果将其中一个三角形放大,两个三角形是怎样的关系呢?

图2
【设计意图】“一线三等角”中最特殊的一种情况是3个90°角,笔者联想到是否能从全等入手,因此利用几何画板软件从学生熟悉的勾股定理入手,动态展示其中相邻的两个全等三角形,接近学生的最近发展区,从而导入新课.
(2)大胆猜想,类比总结.
探究1:①观察图3,猜想△ABC与△DAE的关系,并进行证明;②猜想符合怎样的条件时,上述的结论成立.
探究2:观察图4,若∠C=∠E=∠BAD=60°时,上述结论是否成立?并说明理由.若∠C=∠E=∠BAD=45°时,是否依然成立呢?

图3

图4
探究3:观察图5,若∠C=∠E=∠BAD时,上述结论是否成立?并说明理由.
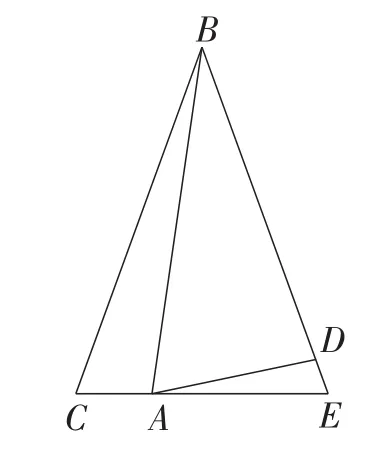
图5
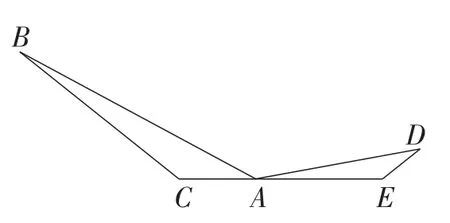
图6
探究4:观察图6,若∠C=∠E=∠BAD是一个钝角时,上述结论是否成立?并说明理由.
思考:根据4个探究,你能得出什么结论吗?
【设计意图】美国著名数学家波利亚曾在《数学与猜想》中指出,要成为一个好的数学家,你必须首先是一个好的猜想家.可见猜想对创造性发明的重要性,本节微课的4个探究按照从特殊到一般的方法,小坡度、密台阶,层层推进,这样设计就是始终在学生的“最近发展区”内探究,有利于学生步步登高,逐步让学生经历观察、实验、猜想、归纳、论证的过程,符合学生知识的建构规律,体会类比思想,最后思考升华知识,总结结论,进而得到“一线三等角”的概念及基本模型.
鉴于角度的任意性,利用几何画板软件动态展示,方便学生体会各角度间的变化,缩短讲授时间,体会知识的本质和内涵,提炼知识的精髓,进而得出结论.
(3)火眼金睛,链接中考.
例1如图7,在边长为9的正三角形ABC中,BD=3,∠ADE=60°.则AE的长为______.
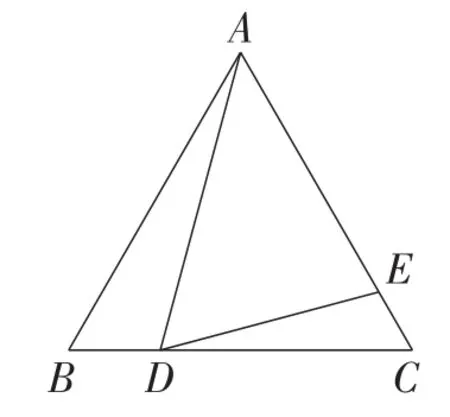
图7
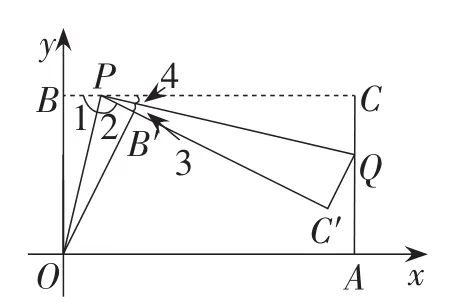
图8
例2如图8,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,A(11,0),B(0,6),点P为BC边上一个动点(点P不与点B,C重合),经过点O,P折叠该纸片,得到点B′和折痕OP,经过点P再次折叠该纸片,使得点C落在PB′上,得点C′和折痕PQ,若BP=t,AQ=m,试用含有t的式子表示m.
【设计意图】鉴于微课的时间限制,例题的选择必须短小精悍,具有针对性、典型性和可研究性,而中考试题是中考复习的指挥棒,例题的选择是否恰当对小专题微课的成败至关重要,针对重点内容,不仅要巩固基础知识和基本技能,还要有延伸性和研究性.美国著名数学家波利亚曾说过,一个专心的、认真备课的教师能够拿出一个有意义的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.首先例题的选取应在学生的“最近发展区”内进行选择,然后再逐层递进,深入挖掘.本节微课选取的例1贴近探究2,根据相似列出方程求解模型,主要让学生熟练运用基本的“一线三等角”模型.例2的主要目的在于拓展延伸.首先,学生能否顺利找出基本图形,关键是分析关键词“折叠”的结论.其次,是用函数模型来刻画,这一步对于学生也是一个提升.
本节微课应当注重分析关键词和基本图形的由来,能利用方程和函数建立模型,围绕通性、通法,建构知识“核心内容”网络,提高微课效益,提升学生解决问题的能力.
(4)归纳总结,感悟思想.
问题:通过本节课,你学到了哪些知识?在解决问题的过程中感受到了哪些思想?
【设计意图】反思探究过程和例题,理解和掌握“一线三等角”的结论及证明方法,掌握基本图形,感悟类比思想、从特殊到一般的思想,体会利用“一线三等角”这一几何模型解题的要领.
(5)巩固模型,反思升华.
思考:如图9,∠C=∠E=∠BAD,点A是CE中点.问:图中有多少对相似三角形?

图9
【设计意图】复习课既要使知识有一个基本点,又要使知识有一个生长点,基本点是根基,而生长点是发展的必要条件.著名数学家波利亚指出,数学问题的解决仅仅只是一半,更重要的是解题之后的回顾,如果没有了反思,他们就错过了解题的一次重要而有效益的方面.解题后的反思可避免解题的错误,优化解题方法,发现更多的问题,提高学生分析问题、解决问题的能力,培养学生思维的深刻性、广阔性和灵活性.笔者提出的这个思考是对“一线三等角”模型的巩固和升华,旨在让学生建立知识网络,与其他的相似进行紧密的练习.
二、微课的创作及使用说明
创作说明:
(1)课题的选择应以中考试题为根本,尤其是将中考的重点、难点制作成微课,及时完善、更新、拓展,建立涵盖中考数学系列专题的微课系统;
(2)要避免偏题、怪题的制作,否则既浪费教师时间,又给学生造成学业负担;
(3)教学设计要科学合理,从旧知进行导入,加强知识之间的联系,建立知识体系;
(4)教学设计要有反思、升华的内容,或迁移到其他专题或精华提炼,能够抛砖引玉,引导学生拓展、提高.
使用说明:
(1)使用地点和时间应根据具体的内容设定,可上课观看,也可课前或课后观看.例如,较难的专题可布置给学生课前观看,上课着重解决观看视频后未能解决的问题、存在的困惑或发现的新问题;拓展资源可让学生课后观看,通过书面测验等方式检验效果;易懂的内容可在课上观看,观看后再探究.
(2)针对课前和课后使用微课,可以让学生通过手机或平板电脑随时随地观看微课,并结合聊天工具进行师生之间和生生之间的交往互动,既为学生创建了自主探索的环境,又为学生提供了交流、质疑、解决问题的平台,促进学生积极思考、自主探索、合作交流等学习习惯的养成.
(3)观看对象也要有选择性,对于较难的内容,可供优等生课后观看,避免出现揠苗助长的现象,使学困生和中等生出现厌恶情绪,对于中等难度或简单内容,可让全班学生观看.
(4)学生在使用微课时,也有一个逐步适应的过程,教师的指导、点拨要到位,如何抵制游戏的诱惑,也需要教师加以引导.
(5)要注意学生学习驱动力的养成,避免强加给学生,占用学生过多的时间.
[1]沈岳夫.知识与能力并重思想与经验齐驱:初中数学专题复习“组块式”教学模式初探[J]. 中学数学,2013(22):22-24.
[2]周丽霞.基于学生主体论的微课数学教学模式研究[J]. 牡丹江教育学院学报,2015(4):69-70.
[3]孙丽梅,吴华.现代信息技术支持下的数学微课教学[J].科教导刊(中旬刊),2013(12):65-66.
[4]赖艳,侯咏娴,赵姣姣.翻转课堂初探:微课在小学数学中的应用[J].中小学信息技术教育,2014(3):36-39.
2017—06—23
康丽(1987—),女,中学一级教师,主要从事数学学科教学研究.

