数学实验教学是培养数学核心素养的有效路径

殷容仪

（江苏省苏州市教育科学研究院）

数学实验教学是培养数学核心素养的有效路径

殷容仪

（江苏省苏州市教育科学研究院）

初中数学实验是学生动手、动脑，以“做”为支架的教与学的活动方式，是一种发现数学结论、理解数学知识、验证数学结论的数学活动，其核心价值是手脑协同、启思明理．数学实验教学能体现学生自主学习和主动探究精神，对于培养学生的实践能力和创新意识有重要意义.数学实验教学有利于学生数学思维的发展，有利于学生数学核心素养的形成，是培养学生数学核心素养的有效路径．

数学实验；核心素养；有效路径

初中数学实验是学生动手、动脑，以“做”为支架的教与学的活动方式，是在教师的引导下，运用有关工具通过具体操作在认知和非认知因素的参与下进行的一种发现数学结论、理解数学知识、验证数学结论的数学活动，其核心是手脑协同、启思明理.

本文试图向读者介绍一个源于书本的几何图形的剪拼实验.这个实验的意图是想让学生在通过动手剪拼的实际操作及不断动脑思考、探索的过程中，把握数学规律的内在本质，发现一个重要的数学结论，即波尔约·盖尔文定理：若有两个平面图形F与H，将F适当剖分为有限块，它们重新组合后可以得到图形H，就说F与H剖分相等，记作F～H.对初中学生而言，用“剪拼相等”来代替“剖分相等”这一说法，或许比较符合学生的认知水平，上述定理换个说法就是：两个面积相等的任意多边形总可以互相剪拼.

这个实验操作有较大的自由度和思维空间，能体现学生自主学习和主动探究精神，能凸显出手脑协同、启思明理的数学实验的核心价值，对于培养学生的实践能力和创新意识有重要意义，有利于学生数学思维的发展，有利于学生数学核心素养的形成，是培养学生数学核心素养的有效路径.

一、问题与操作

苏科版《义务教育教科书·数学》八年级下册“9.5三角形的中位线”开始就设计了这样一个问题情境.

问题1：怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？

具体操作如下：如图1所示.

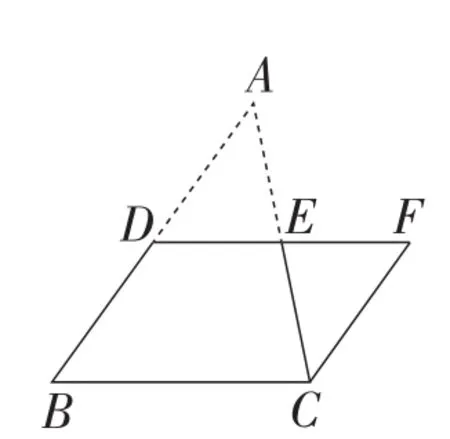
图1

（1）剪一个三角形（纸片），记为△ABC；

（2）分别取AB，AC的中点D，E，连接DE；

（3）沿DE将△ABC剪成两部分，并将△ADE绕点E按顺时针方向旋转180°到△CFE的位置（实际上就是把△ADE剪下来，拼到△CFE的位置处），可得▱BCFD.

我们继续追问.

问题2：怎样将刚才得到的平行四边形纸片剪成两部分，使分成的两部分能拼成一个矩形？

具体操作如下：如图2，在▱ABCD纸片中，过点D作DE⊥AB，垂足为点E，把△AED剪下来，拼到△BFC处，可得矩形EFCD.

我们不难发现，这两次动手实验的结果是通过剪拼改变了图形的形状，但不改变前后图形的面积，问题的数学本质其实就是用三角形可以等面积地剪拼成一个平行四边形或矩形.

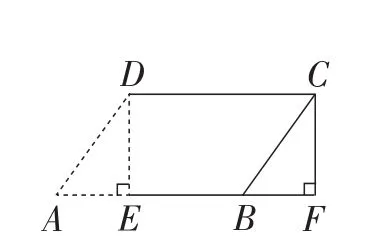
图2

二、“启思”则能“明理”

我们进一步追问.

问题3：两个面积相等但不全等的矩形是否总可以互相剪拼？

这是波尔约·盖尔文定理推导过程中最为艰难的一环.问题看似简单，但仔细研究一下，便会发现要直接完成这样的剪拼，几乎是不可能的（除非出现的是特殊情况，如要剪拼得到的新矩形有一条边长是原矩形纸片某一边长的二分之一、三分之一……），此时就需要教师给予学生一些必要的引导与提示.

这个就是“启思”，从动手操作走向动脑思考.

启思1：先把问题数学化，有一块矩形纸片ABCD（如图3），设AB=a，BC=b，a＞b.我们现在要用这张纸片等面积地剪拼成一个新的矩形，要求新矩形的较长边为c.显然，c＞b总是成立的.

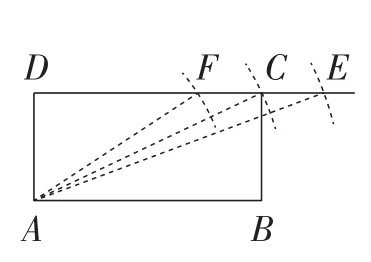
图3

启思2：再把问题适当转化，既然直接剪拼成一个新的矩形难以实现，那我们就退而求其次，能否先剪拼成一个平行四边形呢？并且使得这个平行四边形的一条边长为c，然后依照图2的剪拼方法，即可得到满足要求的新矩形，这个灵感来自于问题2.

如图3，延长矩形ABCD的DC边，以点A为圆心，c为半径作圆弧，不难发现，当（即为矩形ABCD的对角线长）时，圆弧与DC的延长线有交点，不妨记为点E；当时，圆弧与DC边的交点恰好为点C；当时，圆弧与DC边有交点，不妨记为点F.

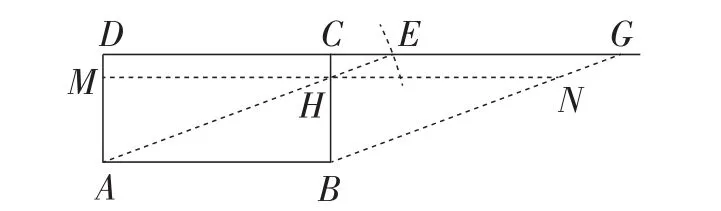
图4

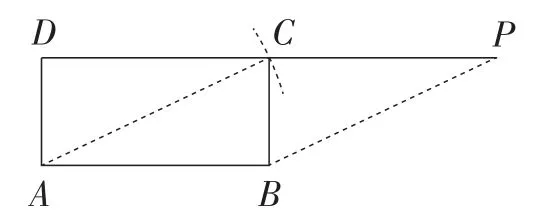
图5

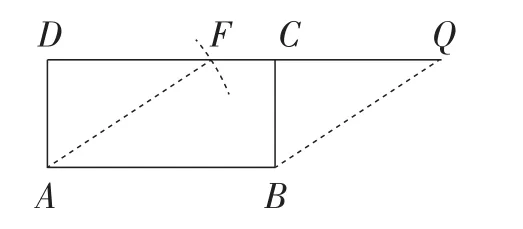
图6

由此可知，一个长为a，宽为b（其中a＞b）的矩形纸片ABCD可以等面积地剪拼成一个新的平行四边形，这个平行四边形有一条边的长度为c（其中c＞b）.根据问题2的解决方法，我们可以知道这个平行四边形又可拼接为有一条边长为c的矩形.

至此，问题3得以解决，但这个问题的解决对波尔约·盖尔文定理的推导有什么样的帮助呢？

我们知道，对于任意一个面积为S的n边形（n＞3），过它的一个顶点并沿其对角线剪开，就可以得到（n－2）个三角形，根据问题1，2，3及其推导过程，这（n－2）个三角形最后总可以剪拼成一个面积为S的矩形.由此可知，两个面积相等的任意多边形总可以先剪拼成两个面积相等的矩形，而问题3又告诉我们，这两个面积相等的矩形总是可以互相剪拼的，这样就解决了两个面积相等的任意多边形总可以互相剪拼这个问题.

从上述推导过程中我们可以发现，问题3就像是问题的“心脏”，抓住了问题的“心脏”，所有的一切都显得浅显了许多，学生就能轻松明白其中的道理，这个就是所谓的“明理”.

我们可以用如图7所示的结构图再次予以简单说明：面积为S的多边形F可以等面积地剪拼成矩形A，面积为S的多边形H可以等面积地剪拼成矩形B，而根据问题3的结论，面积相等的矩形A与矩形B是可以互相剪拼的，所以面积为S的多边形F与面积S的多边形H是可以互相剪拼的.

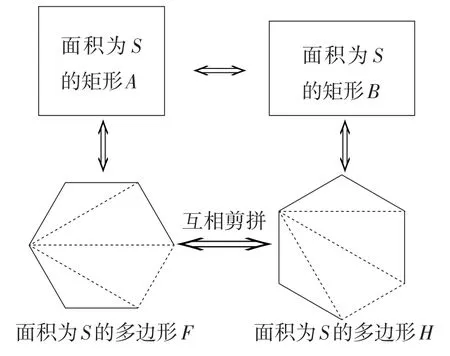
图7

三、“明理”方能“解惑”

数学实验能直接刺激大脑进行积极思维，它不仅能帮助学生理解所学的概念，还能让学生通过亲身实践真切感受到发现的快乐，在过程中学会思考，学会创新.本文的目的当然不只是要给学生介绍一个波尔约·盖尔文定理，正所谓“项庄舞剑，意在沛公”，在定理的推导过程中，我们要争取让学生充分了解数学思维和演绎推理的典型特征，争取让学生深刻体会到数学思想方法在解决数学问题过程中不可或缺的地位，争取让学生深入体验数学家研究数学问题的心路历程，争取让学生真切感受数学的应用价值，这种经历，对中学生来说是难能可贵的.只要给学生以一定的时间和空间，他（她）们身上所具有的潜在的一些能力就会显现出来，创新意识与实践能力的培养也就真正有了落脚点，数学核心素养的培养也就真正落到了实处.

毋容置疑，数学实验教学需要教师及学生投入大量时间，在一般的教学进度下开展这样的教学，会受到很大的限制.然而，实验教学对于培养学生提出问题、解决问题的能力，培养探索能力、创新思维等方面的作用，是目前的常规教学所无法替代的.但问题在于，在目前的环境下，实验教学的频度、教学课时长度的设定应该如何安排更加科学、有效？一个学期多开展几次，可不可以？在课时安排上，如果实验课题的容量较大，那么是否可以为这样的课题安排2课时、或者3课时、甚至更多？这些问题还需要更多的研究、讨论和交流，以便能取得共识，解决疑惑.

［1］董林伟.初中数学实验教学的理论与实践［M］.南京：江苏科学技术出版社，2013.

2017—07—08

殷容仪（1971—），男，中学高级教师，主要从事中学数学课堂教学研究．