“倾听+串联”的数学交流方法探析

刘永东

（广东省广州市天河区教育局教研室）

“倾听+串联”的数学交流方法探析

刘永东

（广东省广州市天河区教育局教研室）

从对话角度认识数学交流，结合具体教学案例，提出“倾听+串联”的数学交流方法，探析其单向互动和多向对话两种交流方式的课堂教学实施方法，其核心是教师通过关注聚焦式的问题预设和对学生讲数学的倾听发现，进而串联思辨，以帮助学生夯实知识技能和增长数学智慧，同时培养数学交流素养.

数学交流；数学对话；倾听串联

编者按：2017年5月，本刊策划推出“初中生数学交流素养培养的方法与途径”专题征稿活动，广泛征集从初中数学课程实施的维度剖析初中生数学交流素养培养目标、定位、方法与策略的论文，广大教师纷纷响应，在征集到的稿件中，有个人研习的成果，也有教研团体讨论的集体成果.通过遴选，先刊发四篇专题文章，其中三篇来自广东教研团队的研究课例及其研究论文成果，一篇来自江苏教师的经典案例研究.后续将继续从专题来稿中择优刊登，请广大读者持续、关注，也请从数学交流素养理论研究，初中生数学表达能力的培养方法，初中师生数学交流素养水平研究等方面赐稿.

一、数学交流价值简析

数学交流是通过数学思维的方式，与文本信息、他人进行数学对话、沟通互动的活动过程.因此，在数学学习活动中，数学交流在形式上是指师生之间、生生之间通过阅读、讨论、辩论、合作等方式理解、提取有效数学信息，通过语言、文字或图形等方式进行有关数学知识、数学思想和数学方法的相互表述和解释过程，以及共同研究数学问题，进行数学实验等的动态过程.其价值在于促进学生对问题的理解，寻找解题思路，增加学生与他人合作的机会，为数学教学提供帮助等，并促进学生数学交流素养的提高.

从对话角度来看，数学交流可以说是数学对话思维的作用，尤其是数学表达和观点探索的过程更是彼此间的对话分享与合作.弗莱雷说过，没有了对话，就没有了交流；没有了交流，也就没有真正的教育.这种展示思考过程，共同探究与对话互动行为的数学交流，其价值在于对数学思维的全部过程进行探索，进而改变交流者在集体中的数学思维进程和方式.

二、数学交流方法探析

当前，教师并非是单纯的知识传授者和解答问题的机器，但教师“主导”教学的积极主动性影响着学生的数学学习.为此，教师需要以“和学生同学”的态度，增加和学生进行交流的机会，提高数学交流意识，和学生互动合作，进行有的放矢的数学交流.而数学交流方法很多，基于“根据自己所说的意思与别人所理解的意思之间的差异产生新想法，就不断会有新的认识与观点出现”的对话认识角度，笔者认为：就数学课堂而言，是对知识的来龙去脉及其蕴涵思想的充分认知，需要教师通过控制和引导学生表达和交流数学观点，在倾听的基础上，串联学生的思维经验，以自身数学智慧去碰撞学生思维，并通过指导学生的自我反刍方式达成数学新认知和增长数学智慧.这种数学交流方法的核心在于“倾听+串联”，它有单向互动和多向对话两种方式，对此，结合“培养初中生数学交流素养的方法研究”课题组的“相似三角形的复习”课例（广州某教师和北京某教师分别主讲）中的两个教学阶段进行探析、阐述：①在知识结构梳理阶段，如何引导学生通过交流形成对核心知识与技能的整体认识？②在例题学习阶段，教师如何倾听学生交流的数学思维，并把学生的交流经验进行串联，引导学生反刍解题方法？

1.单向互动式交流

复习课中的回顾、梳理即是温故知新，如何构建不同层次、不同形式的有意义交流呢？首先，是学生与数学文本之间的静态交流.以题目方式呈现的文本，是一些相互联系的信息揉合，学生在限定时间内自主做题，是一种“以题点知”形式的单向交流.由于文本是静态的，通过做题与文本进行有意义的数学交流，就是一种内心独白，是学生在动手实践中的隐性思考，但显性反映到做题结果上.其次，是学生倾听教师独语（自问自答）的静态交流.数学文本的载体是确定的，而教师独语的载体却是流动的，流动的东西更能体现交流的本质，学生通过认真听讲，把教师对知识的高度抽象转化成自己对数学的理解.这种倾听是单向互动的交流，以广州某教师设计的例1、例2解释如何独语.

例1如图1，在△ABC中，∠C＞∠B，D是AC上一点，在AB边上画出一点E，连接DE，使△ADE与△ABC相似.

图1

图2

例2 如图2，已知△ABC，BC=2，AB=3，∠ABC=90°，在网格内，画出△DEF，其中，直角边DE=6，∠DEF=90°，且与△ABC相似.

学生在例1中出现如图3所示的三种解答结果，如果教师仅仅是表面上对“两角对应相等”的相似判定方法进行复习，则会出现交流的浅层化.教师可通过独语的串联以深化对核心知识的思考.

图3

问题1：在图1中，已知这两个三角形有公共角，同学们都考虑分类，那么该如何分类呢？

若从∠ADE=∠C或∠ADE=∠B来看，分类指向“两角对应相等”，而∠C＞∠B，所以DE2的画法不正确.考虑“两边对应成比例且夹角相等”的相似判定方法，应该还可以指向边的分类.

问题2：若AB=6，AC=4，AD=3，则AE为多少时，两三角形相似？

问题3：如果点D是直线AC上的动点，则与△ABC相似的△ADE有怎样的情况？

通过画草图或看课件演示、观察，可以得到如图4所示的两类基本相似模型.这种兼顾整体，通过问题形式的深度交流，让学生在倾听中认知基础知识和识别基本图形，以达到温故知新的目的.

图4

而例2中，学生会出现多种不同情况（如图5），广州某教师在串联时，呈现学生画图不完整，辨析分类原因不全，点明寻找方法，并以此再现本节课核心知识的框架、结构和主题.这种基于学生作品进行具有针对性的、完善的独语串联，在实践中证实是可行的，学生在师生间深层的数学交流中获得更为理性的认知.

图5

原实录是学生画两个，教师追问后完整画出所有满足条件的图形，并画出一个△DEF5的错例让学生辨析，进而提出把条件∠DEF=90°去掉，结果会怎样？留给学生课后思考.

倾听是双方面的，相互尊重的.学生倾听教师以进行自我对话提升，反之，教师的独语串联适度拓展了学生思维.而串联需要预设和倾听，大概有三种方式：一是在解题中的课内批改和个别指导；二是在合作学习中开展聚焦问题分析的主动沟通；三是在展示交流中及时插话的思维暴露.

2.多向对话式交流

概括是课堂教学的核心，而串联是一种概括方式，是以教师为中心，把新、旧知识和学生之间不同认知经验串联起来，特别是把学生通过感官获得的操作性直接经验和通过内隐思考获得的反思性经验串联，以“异中求同”来抓住问题的本质和共性，以“同中辨异”来区分问题的形式和个性.串联是在建立倾听的基础上，可以开展多向的对话式交流来呈现.以北京某教师的例题设计为例加以说明.

例3如图6，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边BC折叠，使点B落在边OA的点D处，判断△OCD与△ADE是否相似，说明理由.

图6

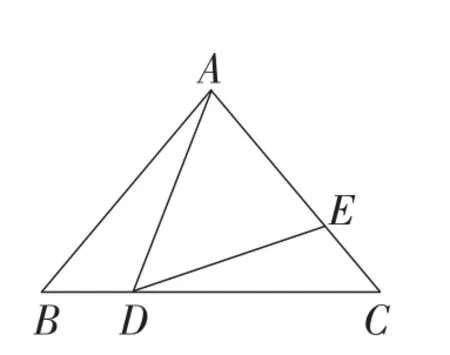
图7

例4如图7，已知，在△ABC中，AB=AC，点D在线段BC上，作线段DE交AC于点E，使∠ADE=∠B.

（1）求证：△ABD∽△DCE；

（2）若AB=9，CD=6，CE=2，求BC的长.

例4有两个变式（略）.姑且不论题目选择的合理性，就题而言，可开展基于学生经验的大串联，以建立数学知识之间的联系，即弄清知识的来历，以及知识前后关联的线索：例3中，若OC=8 cm，OA=10 cm，如何求AE的长？显然，在直角三角形中，已知两边长可以求出第三边，或已知一边长和另两边的关系式，可利用勾股定理与方程思想相结合进行解答（经验1）.而勾股定理的证法多是源于不同图形之间的面积关系推导得出，因此，可用面积法求解，即S△AED=S梯形OAEC-S△OCD-S△CDE（经验2）. 又由△OCD∽△ADE，也可列式求解（经验3）.这三个方法均是在几何图形中寻找等式求解.然而，在图8中，当把矩形两个顶点A，D在保持∠EPF=∠B=∠C的情况下平移，就会出现两种情况，这时只能是运用相似求解线段长，如例3的解题方法（经验4）.在例4和变式中发现一个基本模型，即三个顶点在同一条直线上的三个角相等，则会出现两三角形相似的结论（经验5）.同时注意到这三个等角都在直线的同一侧，也即两个三角形在直线的同侧，进一步联想，会不会在异侧时也有这个结论呢？

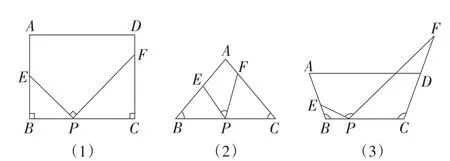
图8

提示学生画出如图9所示的图形加以判断，引导学生形成经验6.

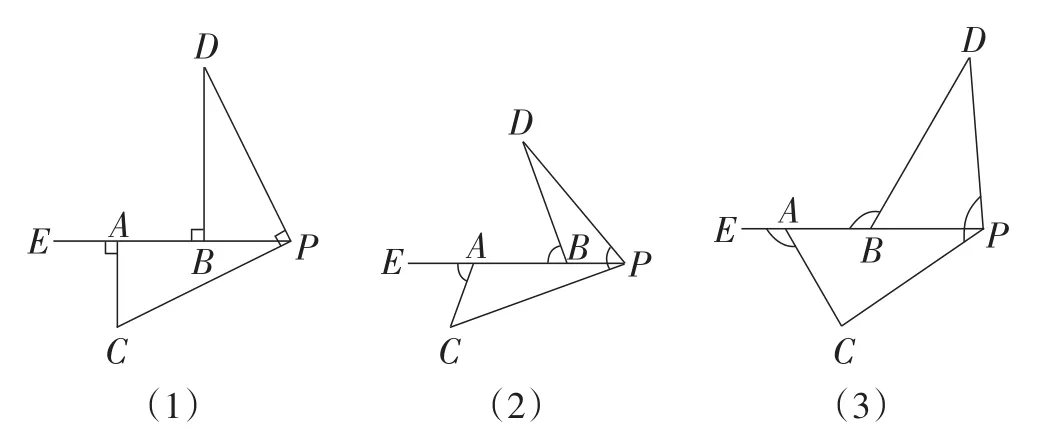
图9

以上串联是把学生学到的知识再现，并与现有解题本源相结合的最佳时机，引导学生学会概括一类事物的本质属性，不仅关注对题目的求解过程和题型归类的浅层次概括，还关注了过程、方法、目标的概括.这恰好是数学交流的关键点和切入点，需要慢下来，给学生通过自主学习和探究体悟的时间，需要群体对话的多向互动交流.这种串联，是借助个人或小组活动不断的交流以反刍问题的内涵，将学生的思考引向深入，而学生参与反刍，本身也是一种自我对话的反思交流.

三、预设和倾听的实践思考

串联需要预设和倾听.如何预设和倾听，才能体现一种“有意义学习”的数学思维串联，有两点实践思考.

1.“聚焦式”的问题预设

笔者曾对中、美两节同课异构的课例进行课堂提问的比较，发现提问总次数相当，中国课堂使用更多事实性提问获得教师期望的答案，而美国课堂中使用更频繁的推理性问题（中国11%，美国34%）来激发学生思考，并表达他们的想法，提出更多开放性的问题（中国7%，美国12%）来鼓励探索.研究发现，美国课堂中的数学交流更为充分.基于此，教师需要注意立足理解数学，寻找和预设有意义的具体问题，用追问或提问等对话促进学生交流.不预设期待给学生回答“对错或是否”的问题，也尽量避免预设靠记忆描述数学事实或解题过程的事实性和程序性问题，而是预设期待让学生自己提出问题或对自己的猜想解释说明与解题的推理性问题.这种交流是一种聚焦数学问题的对话式互动，让学生充分展示他们的思维过程，避免了单向传递数学信息和意义的漏斗式交流.

2.“讲数学”的倾听发现

课堂上“讲数学”，既可以是讲数学题、讲数学概念，也可以是讲数学发现等，让学生先产生一个想法并详细加以阐述，接下来又有其他学生对这一想法进行补充，并运用数学符号，系统、严谨的表达方式讲述思维过程，教师通过倾听和发现，思考“有意义”的串联方式.由此，需要给学生创造讲数学的机会，可以从起始年级开始培养与训练.初始阶段，可以缩小数学交流范围，预先设定一个目标，并做一个思维约束，虽然可能阻碍自由交流，但可以让师生感知数学思维的发生，又能在相互反应中觉察出微妙的区别和联系，促进学生规范运用数学语言表达自己的看法，等到学生的数学交流和表达能力大幅度提升后，再尽可能开放进行，让思维意识像潺潺之水，流淌于师生之间.

四、结束语

“倾听+串联”的数学交流，不是简单的协商和接纳，而是平等的沟通、生态的互动、理解的包容和精神的共享.它是一种开放的数学知识建构，是一种聚焦核心观点的对话式交流，有利于培养学生的数学交流素养，并能有效增长学生的数学智慧.

［1］许世红.初中生数学交流素养及其测评标准探索［J］.中学数学研究（华南师范大学版），2016（16）：封二，1-4.

［2］戴维·伯姆.论对话［M］.王松涛，译.北京：教育科学出版社，2006.

［3］黄荣金，吴平生，刘永东.相同课题，不同学习机会：基于中美两节示范课的比较研究［J］.数学教学，2014（10）：1-5，37.

2017—07—25

广东省教育科研“十二五”规划2015年度重点项目——基于PISA数学素养测评视角培养初中生数学交流素养的方法研究（2015ZQJK035）.

刘永东（1971—），男，中学高级教师，衡阳师范学院客座教授，华南师范大学兼职硕士指导教师，主要从事初中数学教材、教法和区域教研研究.