问题引领，交流拓展，复习升华——“一次函数（复习课）”的教学思考

吕同林

（江苏省泰州中学附属初级中学）

问题引领，交流拓展，复习升华
——“一次函数（复习课）”的教学思考

吕同林

（江苏省泰州中学附属初级中学）

复习课是数学教学的重要一环.有效的数学复习课，应关注学情和组织方式，还要关注学生的学习情感，努力做到“情理交融”.复习课一要优化问题设置，聚焦复习的有效性；二要突出基础建构，聚焦复习的再生性；三要深化交流活动，聚焦复习的交互性.

问题设置；基础建构；交流互助

微信扫描二维码线上观看本文配套微课

复习课是数学教学的重要一环，数学复习课的形式是多样的，不同的复习方式所达到的目标也会有所不同.笔者就“一次函数”的复习课，探索问题引领.交流拓展的数学复习课，受到听课教师的肯定.现就教学的一些体会，与同行分享.不妥之处，恳请指教.

一、教学过程再现

1.基础回顾

已知：y是x的一次函数，当x=2时，y=1；当x=-2时，y=3.

问题1：求y与x的函数关系式（学生自主练习）.

师：你解决此问题运用的是什么方法？

生1：待定系数法.

师：你为何运用待定系数？

生1：因为y是x的一次函数，依据一次函数的定义.

师：一次函数是怎样定义的？

生1：函数y=kx+b（k，b为常数，且k≠0）叫做一次函数.

师：非常好！一次函数有一种特殊形式，谁能说一说？

生2：当b=0时，函数y=kx（k≠ 0）叫做正比例函数，也称y与x成正比例.

师：一次函数的定义是我们研究一次函数问题的基点和源头，请完善知识结构表的定义板块.

生3展示，略.

跟踪练习：下列函数哪些是一次函数？哪些不是？哪些是正比例函数？

师：此函数的图象是什么图形？你是怎样画的？

生4：它的图象是一条直线，我选取两点（0，2）（4，0）作直线，依据“两点确定一条直线”.

师：反过来，坐标系中的直线，表示的都是一次函数关系吗？

生5：与坐标轴平行的直线，不表示一次函数关系.

师：交流一下结构表中图象部分的核心知识.

生6展示，略.

跟踪练习：一次函数y=kx+b的图象如图1、图2所示，指出k，b的符号.

图1

图2

问题3：当x______时，y=0；当x______时，y＞0； 当x_____时，y＜0；

师：你是如何得到的？

生7：我根据题意，通过列方程或不等式得到.

生8：我是利用观察图象得到的，y=0是找图象与x轴交点的横坐标的值；y＞0是找出图象位于x轴上方部分所对应的点的横坐标范围；y＜0是找出图象位于x轴下方部分所对应的点的横坐标范围.

师：非常好！可以使用列方程或不等式求解的代数方法，也可以通过观察图象的方法来解决问题.

跟踪练习：一次函数的图象如图3所示.

（1）当x_____时，y=1；

（2）当x_____时，y＞1；

（3）当x_____时，y＜1.

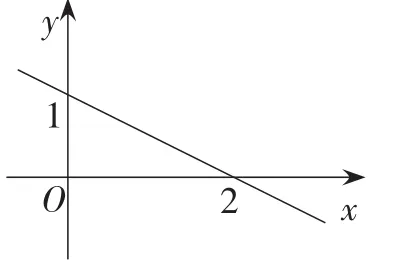
图3

问题4：点A（a，m），B（b，n）在函数图象上，且a＜b，试比较m，n的大小关系（不少于两种方案）.

师：你是如何比较m，n的大小关系的？

生9：我是根据一次函数的性质比较m，n的大小关系的，此时，y随x增大而减小，a＜b，则m＞n.

生10：我是利用图象做比较的，a＜b说明点A在点B的左侧，画出A，B两点的大致位置，并由此找出对应的m，n，于是m＞n.

师：非常好！想一想，我们还可以用什么方法比较两个数的大小？

师：太棒了！这里比较大小，可以利用函数性质、函数图象以及作差等方法来解决，多角度思考是解决问题的有效途径.交流一下，一次函数常用的数学方法（其他同学可以补充）.

生12展示，略.

师：你是如何平移的？

生13：图象与y轴交于点（0，2），于是将其向下平移2个单位即可通过原点.

师：还有其他的平移方式吗？

生14：图象与x轴交于点（4，0），于是将图象向左平移4个单位即可通过原点.

生15：平移可以考虑上下和左右的方式.例如，图象经过（2，1），于是先将直线向下移动1个单位，再向左平移2个单位，图象即通过原点.移动方式不唯一.

师：非常好！平移方式具有多样性，较为简洁的方式是单一移动方式.在图象平移的过程中，一次函数关系式中的哪些量发生变化，哪些量没有变化？

生16：k值不变，其决定变量间的变化特征；b值改变，其决定图象的位置.

师：将数学核心知识和方法绘制成如表1所示的结构表（树）有助于我们整体建构数学的知识与方法，通过查漏补缺，不断完善知识的方法体系，深化对数学的理解.这项工作在复习时显得尤其重要.

表1：基础回顾环节完成的核心内容结构表

2.例题研讨

（1）若y与x的函数关系如表2所示.

表2

根据表中数据，能否找到一个函数关系式，反映此表格中两个变量之间的关系.

师：你发现的是何种函数关系？怎么得出的？

生17：将表中的对应值作为点的坐标，描出相应的点，这些点在一条直线上，猜想其为一次函数关系.

生18：分析表中y与x的数量关系，得出y=3x+1.

师：积累和丰富数学思维活动经验，有助于提升我们的数学素养和应用数学能力.

（2）如图4，直线AD，BC交于点P，根据图中提供的信息解决下列问题.

图4

①求线段AB的长；

②求△PCD的面积.

3.小结感悟

略.

4.作业训练

略.

二、教学感悟

数学复习课的教学活动，不宜进行知识的简单再现，这样的课堂“枯燥”而缺少“引力”；也不宜进行大量习题的演练，这样的课堂“零散”而缺乏“活力”.有效的数学复习课应关注知识系统的建构和完善，强化数学方法的再生和优化，促进数学学习力的不断发展和提升.

1.优化问题设置，聚焦复习的有效性

问题是数学的心脏.在数学复习课的教学活动中，例题的选择、问题的设置等都影响着复习的效果.例题选择的典型性、针对性、连贯性、拓展性等已成共识，而问题设置的启发性、探究性、思考性、可操作性等关乎着例、习题的复习价值.因此，数学复习课中，例题的选择、问题的设置等都需要教师精心预设，聚焦复习的全过程，以期达成复习课的教学目标.

本节课，主要安排了两组数学活动；一是基础回顾；二是例题研讨.基础回顾主要是针对复习内容的核心知识和主要方法，以及本班学生的学情而精心设置的问题链.学生通过具有连贯性、思考性、针对性的典型问题的探究和研习，不仅建构和完善数学知识结构，而且学会基于多角度思考问题的方法，逐步养成良好的思维品质.例题研讨部分对不同方式（如表格、图形等）所提供的数学信息进行分析和处理，进一步提升学生阅读和理解数学信息的能力，进而积累数学活动经验，优化问题解决策略，发展数学核心素养.

数学是思维的体操.数学复习课的问题设置应聚焦学生的思维发展，既要关注思维的恒常性（通解、通法），又要关注思维的多样性，还要关注思维的深刻性（基于本质）.设置的问题应具有思考性、探究性，彰显问题的价值，提升复习课的效率.

2.突出基础建构，聚焦复习的再生性

数学的学习过程是一个螺旋上升、系统逐步完善的过程.数学的复习过程是学生基础结构进一步完善和发展的过程.数学复习课应着眼于基础结构的重组、优化和完善.

本节课通过基础回顾的一组问题，引领学生自我回顾和梳理核心知识、方法要点，并形成核心知识结构表（知识结构树），过程自然，结论简约.学生学得主动，学得积极.通过归纳和交流，对于零散的、遗忘的那部分内容，学生通过自身的努力实现了系统的再建构、再生成、再完善，进而发展数学能力，达成复习的目标，实现复习的价值.

数学复习课还应关注本班学生的学习实际，突出薄弱环节的训练.对学生易混淆和易错的方面有针对性的进行比较和甄别，强化核心知识和方法的完善，实现数学能力的再提升.

3.深化交流活动，聚焦复习的交互性

《义务教育数学课程标准（2011年版）》指出：教学活动是师生积极参与、交往互动、共同发展的过程.每位学生的学习方式、思考问题的角度、问题解决策略的选择等都可能有所不同.课堂教学时，教师适时给予学生自主思考和交流展示的机会，有助于学生思维的碰撞、智慧火花的生成、思想的共鸣.因智生慧，以慧生情；因情悟理，以理生智，促进生生共同成长.数学复习课信息量较大，问题解决的方法丰富多样，教师的一言堂不利于学生的成长.教师适时为学生提供交流互动的机会，通过生生之间互帮互助，不断完善思维结构，深化数学理解，提升数学素养，既达成复习目标，又学会复习的过程和方法.

本节课问题的解决，充分依靠和信任学生，通过交流展示，不仅解决了问题，而且激发了学生多角度思考问题的热情，同时还构建了和谐的师生关系，树立了学生学习数学的信心.交流活动不能简单的回答怎样做，而是要阐明为什么这样做.不仅交流问题的结论，更要交流得出结论的思考路径，这样的交流才有意义和价值.

当然，数学复习课的形式较为丰富.不同的教师、不同的知识内容、不同的学情所采取的教学方法会有所不同.但完善知识结构、培养数学能力、积累数学活动经验、激发数学学习热情、形成数学核心素养、促进学生的健康成长是我们数学教师的共同追求.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］叶澜.让课堂焕发生命的活力［J］.教育研究，1997（9）：3-8.

［3］章建跃.创新推动课程改革，全面提高教育质量［J］.中国数学教育（初中版），2016（4）：2-11.

［4］罗增儒.数学的领悟［M］.郑州：河南科学技术出版社,1997.

［5］石志群.例谈先行组织者的途径与功能［J］.数学通报，2016（2）：9-12.

［6］钱德春，吕同林.初中数学情理交融课堂教学的实践研究开题报告［J］.中学数学教学参考（中旬），2014（8）：55-58.

［7］夏志辉，李宽珍.以变式探究 创高效微课：一节高三数学小专题复习微课的设计评析［J］.教学月刊·中学版（教学参考），2014（10）：45-48.

2017—07—11

江苏省教育科学“十二五”规划（2013）立项课题——初中数学“情理交融”课堂教学实践研究（E-c/2013/011）.

吕同林（1965—），男，中学高级教师，主要从事课堂教学、学习评价研究.