基于Parzen窗的水下无线传感器网络目标定位方法

庞菲菲 张群飞 史文涛 韩 晶 孟庆微



基于Parzen窗的水下无线传感器网络目标定位方法

庞菲菲*①张群飞①史文涛①韩 晶①孟庆微②

①(西北工业大学航海学院 西安 710072);②(空军工程大学信息与导航学院 西安 710077)

水声通道复杂多变，使得水下无线传感器网络中节点出现失效的情况，影响了多节点的目标定位性能。为解决这一问题，该文提出一种基于Parzen窗的方位交线定位方法。该方法利用Parzen窗分析所有交点的分布特征，估计目标可能出现在某个位置的概率，将概率最大值对应的点作为目标的估计位置。由于概率分布是非线性、多峰值的，采用带有惯性权重的粒子群算法去求解。仿真实验结果表明，所提方法能够在节点失效的情况下获得较高的目标定位性能，具有较好的鲁棒性。

水下无线传感器网络；目标定位；方位交线方法；Parzen窗

1 引言

对水下目标精密定位是水下无线传感器网络的重要任务之一，可以为水下目标的安全航行、打捞救生以及海洋资源开发提供基础[1]。水下无线传感器网络(Underwater Wireless Sensor Networks, UWSN)通过传感器节点协同探测和融合目标信息来实现目标定位。根据传感器节点是否发射信号，可以将定位技术分为主动式[2,3]和被动式[4,5]。被动式定位技术不主动发射信号，利用目标辐射噪声进行定位，具有良好的隐蔽性，成为当前研究的热点。

被动定位的方法主要包括时差定位[4,6]、强度差定位[7,8]和方位交线方法[5,9]。在复杂的水下环境中，时差定位方法容易受到声线垂直方向弯曲的影响；强度差定位方法在远程目标低信噪比条件下强度(信噪比)估计误差较大；方位交线方法依据传感器节点估计目标的方位角进而确定目标位置，是较为可靠的方法，受到了广大学者的关注。目前关于方位交线法的研究工作主要集中在两个方面：一是研究采用不同的方法对目标定位方程求解，如最大似然估计[10]、约束最小二乘方法[11]；另一类是依据权重对测量数据进行加权融合[12]。这些方法都是分析如何减小方位估计误差对定位结果的影响，虽然可以较好地提高定位精度，但是并不能有效去除部分节点失效对定位结果的影响。

近年来有些学者通过分析方位交线的交点分布特征实现目标定位，为目标定位提供了新的思路。文献[13]按照密集程度(距离平方和)对所有交点进行数据质量分析，将高质量数据(密集程度高的数据)的中心作为目标估计位置，获得了较好的定位效果，仿真一节中会将本文方法与之进行对照；但是由于在对样本点的性质分析中作了近似处理，一定程度上影响了目标的定位精度。文献[14]和文献[15]通过分析交点的概率分布，消除多目标定位时方位线相交产生的虚假点。受此启发，将概率计算运用到单目标定位中，如果能够准确描述交点分布情况，则可能进一步提高对单目标的定位精度。基于此，本文提出了一种基于Parzen窗的方位交线定位方法：利用Parzen窗方法分析方位交线的所有交点分布特征，估计目标可能出现在某个位置的概率，将概率最大值对应的点作为目标的估计位置。由于概率分布是非线性、多峰值的，采用带有惯性权重的粒子群算法求解该最大化问题。仿真实验表明，相较其它方位交线方法，本文方法有较稳定的定位性能；并且可以有效减小部分节点失效对定位结果的影响，鲁棒性更好。

2 基于Parzen窗的目标位置概率密度估计

2.1方位交线方法的交点分布特征分析

方位交线法的定位原理是：在2维平面内，每个节点分别对目标进行方位估计，然后分别将方位线两两相交，得到的交点即是目标的位置，如图1所示。图中，节点A(x,y)、节点A(x,y)所测目标方位角分别为和。目标位置(0,0)坐标可由式(1)所示的两条方位线相交获得

解得

(2)

实际探测中，UWSN的每个节点周期性地对目标进行方位估计，并将估计结果发送给融合中心。融合中心利用方位交线方法对目标进行定位。由于每个节点对目标方位估计时存在误差，当(>2)个节点对同一个目标进行观测时，最多可产生个交点。.

图 1 方位交线法的定位原理

文献[13]表明：测向线所给信息是目标定位和分选的全部依据；一条测向线说明目标可能在离线很近的地方，而很少可能在离线很远的地方。方位线(测向线)越集中的地方，目标出现的概率越大，此处方位线的交点越密集。图2是10个节点(节点位置同表1)同时对在(2000, 2000)的目标进行方位估计，用方位交线方法可产生45个交点，目标出现在交点最密集的区域。从图2中可以看出：在传感器网络中采用方位交线方法对目标进行定位时，目标在各方位线交点最密集处出现的概率具有最大值。因此，可以根据交点的分布特征，对目标可能出现在某个位置上的概率进行估计，即得到关于位置的概率密度函数。概率密度函数最大峰值处对应的点可认为是目标的估计位置。

图 2 方位交线法的所有交点分布情况

Parzen窗无需先验知识，在小样本条件下也能合理地估计概率密度，估计曲线光滑[16]，这里我们将方位线两两相交得到的交点看作个独立样本，采用Parzen窗来估计目标位置的概率密度。

2.2基于Parzen窗的概率密度估计

Parzen窗由Parzen[17]于1962年首次提出，利用已知样本对总体分布密度函数进行估计。其基本思想是利用一定范围内各点密度的平均值对总体密度函数进行估计[18,19]。具体方法是：设为维空间中任意一点，是个独立样本，要用这个独立样本来估计处的概率密度。考虑以为中心，边长为的维立方体，其体积为。为计算落入中的样本数，构造一个窗函数使得当落入立方体中时，；反之。因此，落入中的样本数为

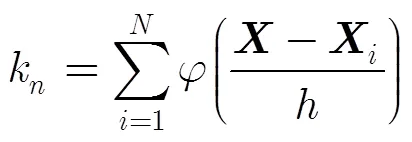
处的概率密度估计值为

(4)

在本文中，只考虑在2维平面上的方位交线定位方法，因此关于目标位置的概率密度函数为

(6)

窗宽系数决定了每个样本处高斯窗函数形状。增大，更光滑，但平均化作用突出，淹没了密度函数细节部分；反之，描述细节分布的能力增强，但易受到随机干扰影响，在概率密度函数上产生伪峰，因此需一个适当的取值，平衡上述两种作用[16]。

由于目标在各方位线交点最密集处出现的概率具有最大值，可将概率密度函数的最大峰值处对应的点作为目标的估计位置。

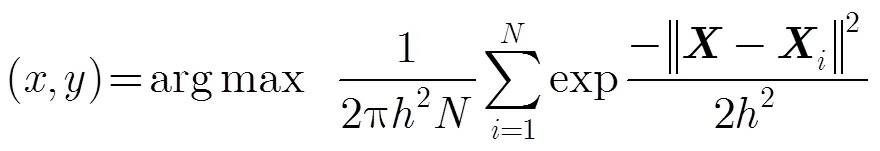
概率密度函数是非线性的、多峰值的，而带有惯性权重的粒子群算法除了具有模型操作简单、设置参数少、算法收敛速度快、高效等优点外，还可以提高跳出局部极值的能力，可以很好地求解多峰值的优化问题[20]。因此本文采用带有惯性权重的粒子群算法去进行求解。

3 定位算法

3.1带有惯性权重的粒子群算法

粒子群优化算法是最早由Kennedy和Eberhart[21]于1995年提出的一种基于群体智能的优化算法。在搜索过程中，为了提高跳出局部极值能力，Shi等人[22]提出了带有惯性权重的粒子群算法(Standard Particle Swarm Optimization, SPSO)。其搜索过程可表示为：粒子群由个粒子组成，每个粒子的位置X代表优化问题在维搜索空间中潜在的解。粒子在搜索解空间时，保存其搜索到的最优位置。在每次迭代中，粒子根据自身惯性、自身经验和群体最优经验调整自己的速度向量，进而调整自身位置。粒子根据式(8)和式(9)来更新速度和自身状态。

(9)

其中，第个粒子在第维的位置为X，飞行速度为v;为迭代序号；学习因子1和2是非负常数，通常1=2=2;1和2是取值介于(0, 1)之间的随机数[22]。为惯性权重，表明粒子原先的速度能在多大程度上得到保留；较大的惯性权重有利于展开全局寻优，而较小的惯性权重则有利于局部寻优。Shi等人[22]经过多组反复实验后，建议采用从0.9线性递减到0.4的策略，通常会取得比较好的算法性能。

3.2 定位算法流程

采用SPSO求解目标位置的概率密度函数最大化问题，将最优解作为目标位置的估计。算法流程见图3所示，具体如下：

步骤1 各传感器节点对目标方位估计，方位线两两相交，产生个交点。

步骤2 SPSO初始化：设定种群规模,1,2,，最大迭代次数max；计算所有交点的中心，在中心附近对粒子的随机位置进行初始化；对速度进行初始化。

步骤3 按照式(6)计算每个粒子的适应值(概率密度)。

步骤4 找出第个粒子的最好位置以及全局最好位置，根据式(8)，式(9)对粒子的速度和位置进行更新。

步骤5 判断是否满足终止条件：如达到最大迭代次数max，则输出当前全局最好位置为最优解；否则返回步骤3。

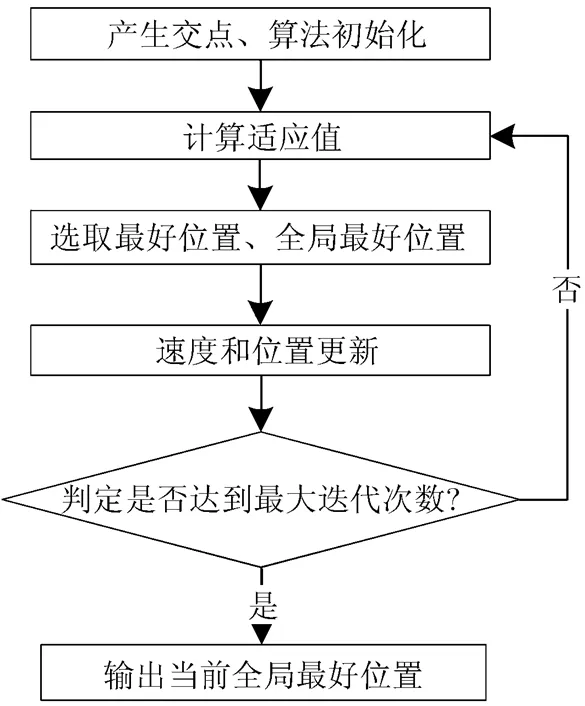
图3 定位算法的流程图

4 仿真

4.1 目标位置的概率密度函数仿真

利用10个节点对位置在(2000 m, 2000 m)的目标进行观测，采用方位交线得到45个交点，见图2。将这些交点作为独立样本，采用Parzen窗方法对目标出现在某个位置的概率密度进行估计，见图5。由图5可以看出：(1)Parzen窗很好地估计了目标位置的概率密度函数，在最高峰处对应的位置(2000 m, 2000 m)是目标真实的位置。(2)目标位置的概率密度函数是非线性的，较难求解。采用SPSO迭代20次，迭代过程见图6，解得的目标位置为(1996m, 2001m)。这说明SPSO算法可以较快地找到目标函数的较优解。

4.2定位精度仿真

目标位于(2000 m, 2000 m)，分别采用本文方法、线性最小二乘估计方法和文献[13]的聚类算法进行200次Monte Carlo仿真，对目标位置估计200次的结果见图7。每次仿真估计出的目标位置距真实位置的误差结果见图8。可以看出，相较线性最小二乘方法和聚类算法，本文估计出的目标位置更集中在真实值附近，定位误差更小。

用均方根误差(RMSE)衡量定位精度。本文方法得到的RMSE≈12.68 m，线性最小二乘方法的RMSE≈14.51 m，聚类算法的RMSE≈17.18 m。在当前的仿真条件下，相比线性最小二乘方法和聚类算法，本文方法的定位精度分别提高了约2 m, 4 m。这说明本文采用Parzen窗方法很好地描述了交点的分布特征，得到了较准确的目标位置的概率函数，比线性最小二乘方法和聚类算法能得到更高的定位精度。

4.3 部分节点失效对定位性能的影响

水声通道复杂多变，会产生节点失效的现象。节点失效有两种情况，一种是无法给出目标方位信息，一种是估计的方位信息误差很大。前者实际上是减少了参与融合的节点数目，后者则会带来奇异点。在这两种部分节点失效的情况下，分别分析两种方法对目标定位精度的影响。

在10个节点中，无法给出目标方位信息的节点数目从0个增加到7个，分别采用本文、线性最小二乘估计和聚类算法计算目标真实位置在(2000 m, 2000 m)时的RMSE变化情况，结果见图9。从图中可以看出，随着不参与融合节点数目的增加，本文的RMSE从12.68 m增加到了24.34 m，而线性最小二乘和聚类算法的RMSE分别从14.51 m, 17.18 m增加到了31.60 m, 32.25 m。相较而言，本文方法仍具有较高的定位精度。不参与融合节点数目的增加意味着交点(样本)数目的减少，而Parzen窗在样本较少时也可以合理地估计概率密度函数，可以较好地估计出目标位置，具有较稳定的定位精度性能。

表1节点的位置分布(m)

节点序号12345678910 x轴坐标18623681561476544153594303329344180169 y轴坐标3259752250735240883295248282745703402

图 7 目标位置估计值

图 8 3种方法的定位误差　　　 图 9 减少参与融合节点的数目对RMSE的影响　　　图 10 大定向误差对RMSE的影响

5 结束语

针对部分节点失效对方位交线定位算法的影响，本文提出了一种基于Parzen窗的定位方法。该方法将所有交点作为独立样本，采用Parzen窗方法估计目标可能出现在某个位置的概率，并采用带有惯性权重的粒子群算法去求解得到目标的位置。仿真实验表明，相比其它方法，本文方法具有更好的定位精度性能；进一步的仿真实验表明，本文方法可以有效减小部分节点失效对定位结果的影响，具有较好的鲁棒性。

定向精度与目标所处方位以及距节点的距离有关，但本文对定向精度的假设比较简单。在下一步的工作中，将研究该算法在定向精度受目标方位与距节点距离影响下的定位性能。

[1] HSC C C, LIU H H, GOMEZ J L G,. Delay-sensitive opportunistic routing for underwater sensor networks[J]., 2015, 15(11): 6584-6591. doi: 10.1109/JSEN.2015.2461652.

[2] BOSSE J, KRASNOV O, and YAROVOY A. Direct target localization and deghosting in active radar network[J]., 2015, 51(4): 3139-3150.10.1109/TAES.2015.140170.

[3] VANDER Hook J, TOKEKAR P, and ISLER V. Algorithms for cooperative active localization of static targets with mobile bearing sensors under communication constraints[J]., 2015, 31(4): 864-876.10.1109/TRO.2015.2432612

[4] NOROOZI A and SEBT M A. Target localization from bistatic range measurements in multi-transmitter multi- receiver passive radar[J]., 2015, 22(12): 2445-2449. doi:10.1109/LSP.2015.2491961.

[5] HE Y, BEHNAD A, and WANG X. Accuracy analysis of the two-reference-node angle-of-arrival localization system[J]., 2015, 4(3): 329-332. doi: 10.1109/LWC.2015.2415788.

[6] POURSHEIKHLI S and ZAMIRI-JAFARIAN H. TDOA based target localization in inhomogenous underwater wireless sensor network[C]. International Conference on Computer and Knowledge Engineering, Mashhad, Islamic Republic of Iran‎, 2015: 1-6. doi: 10.1109/ICCKE.2015. 7365873.

[7] TOMIC S, BEKO M, DINIS R,. Efficient estimator for distributed RSS-based localization in wireless sensor networks[C]. IEEE Wireless Communications and Mobile Computing Conference,Dubrovnik, Croatia, 2015: 1266-12751. doi: 10.1109/IWCMC.2015.7289264.

[8] CHO H and KWON Y. RSS-based indoor localization with PDR location tracking for wireless sensor networks[J].-, 2016, 70(3): 250-256. doi:10.1016/j.aeue. 2015.12.004.

[9] XU J, MA M, and LAW C L. Cooperative angle-of-arrival position localization[J]., 2015, 59(1): 302-313. doi: 10.1016/j.measurement.2014.09.023.

[10] FARMANI M, PEDERSEN M S, TAN Z H,. Maximum likelihood approach to “informed” sound source localization for hearing aid applications[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 2015: 16-20. doi: 10.1109/ICASSP.2015.7177923.

[11] 王燊燊, 冯金富, 王方年, 等. 基于约束最小二乘的近空间雷达网定位算法[J].电子与信息学报, 2011, 33(7): 1655-1660. doi: 10.3724/SP.J.1146.2010.01211.

WANG Shenshen, FENG Jinfu, WANG Fangnian,. Location method of near space radar network based on regularized constrained total least square[J].&, 2011, 33(7): 1655-1660. doi: 10.3724/SP.J.1146.2010.01211.

[12] KUlakowski P, VALES-ALONSO J, EGEA-LOPEZ E,. Angle-of-arrival localization based on antenna arrays for wireless sensor networks[J].&, 2010, 36(6): 1181-1186.doi: 10.1016/j. compeleceng.2010.03.007.

[13] 何友, 王本才, 王国宏, 等. 被动传感器组网变门限聚类定位算法[J].宇航学报, 2010, 31(4): 1125-1130. doi: 10.3873/ j.issn.1000-1328.2010.04.030.

HE You, WANG Bencai, WANG Guohong,. A clustering localization algorithm with adaptive threshold in passive sensor network[J]., 2010, 31(4): 1125-1130. doi: 10.3873/j.issn.1000-1328.2010.04.030.

[14] 胡来招. 定位概率计算在多目标环境下的应用[J].电子对抗技术, 2002, 17(1): 14-18. doi: 10.3969/j.issn.1674-2230.2002. 01.003.

HU Laizhao. Application of passive locating algorithm based on probability in multi-target environment[J]., 2002, 17(1): 14-18. doi: 10.3969 /j.issn.1674-2230.2002.01.003.

[15] 谭坤, 陈红, 蔡晓霞, 等. 基于概率计算的虚假点消除算法研究[J].电子信息对抗技术, 2009, 24(5): 29-32. doi:10.3969/ j.issn.1674-2230.2009.05.007.

TAN Kun, CHEN Hong, CAI Xiaoxia,. Ghost eliminating algorithm based on probability[J]., 2009, 24(5): 29-32. doi:10.3969/j.issn.1674-2230.2009.05.007.

[16] 刘晗, 张庆, 孟理华, 等. 基于Parzen窗估计的设备状态综合报警方法[J].振动与冲击, 2013, 32(3): 110-114. doi: 10.3969 /j.issn.1000-3835.2013.03.022.

LIU Han, ZHANG Qing, MENG Lihua,. Comprehensive alarm method for equipment conditions based on Parzen window estimation[J]., 2013, 32(3): 110-114. doi: 10.3969/j.issn.1000-3835.2013.03.022.

[17] PARZEN E. On estimation of a probability density function and mode[J]., 1962, 33(3): 1065-1076. doi: 10.1214/aoms/1177704472.

[18] MUSSA H Y, MITCHELL J B O, and AFZAL A M. The Parzen window method: In terms of two vectors and one matrix[J]., 2015, 63: 30-35. doi:10.1016/j.patrec.2015.06.002.

[19] 干晓蓉. 模式识别[M].昆明:云南人民出版社, 2006: 43-47.

GAN Xiaorong. Pattern Recognition[M]. Kunming: Yunnan People’s Publishing House, 2006: 43-47.

[20] 李丽, 牛奔. 粒子群优化算法[M].北京:冶金工业出版社, 2009: 25-33.

LI Li and NIU Ben. Particle Swarm Optimization[M]. Beijing: Metallurgical Industry Press, 2009: 25-33.

[21] EBERHART R C and KENNEDY J. A new optimizer using particle swarm theory[C]. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 1995: 39-43. doi: 10.1109/MHS.1995. 494215.

[22] SHI Y and EBERHART R C. A modified particle swarm optimizer[C]. IEEE International Conference on Evolutionary Computation,Anchorage, AK, USA, 1998: 69-73. doi: 10.1109/ ICEC.1998.699146.

庞菲菲： 女，1984年生，博士生，研究方向为水下信号处理.

张群飞： 男，1968年生，教授，研究方向为水下信系处理、水声通信和系统仿真.

史文涛： 男，1985年生，讲师，研究方向为数组信号处理、多传感器与自适应信号处理.

韩 晶： 男，1980年生，副教授，研究方向为水声信号处理、水声通信、水声系统仿真.

Target Localization Method Based on Parzen Window inUnderwater Wireless Sensor Network

PANG Feifei①ZHANG Qunfei①SHI Wentao①HAN Jing①MENG Qingwei②

①(,,’710072,);②(,,’710077,)

In Underwater Wireless Sensor Network (UWSN) the accuracy of target localization suffers from invalid anchors. To reduce the impact, an improved cross-bearing localization method is proposed based on the Parzen window. In this method, the probability of target location is estimated by the Parzen window according to the distribution characteristics of all intersection points, and the target location is selected as the point corresponding to the maximum value of probability. Because of the nonlinear and multi-peak features of the probability distribution, the standard particle swarm optimization method is adopted to solve the problem. Simulations indicate that the proposed method avoids effectively the influence of the invalid anchors on the performance of localization, and has better accuracy and robustness compared with other cross-bearing localization methods in the complex underwater environment.

Underwater Wireless Sensor Network (UWSN); Target localization; Cross-bearing method; Parzen window

TP393

A

1009-5896(2017)01-0045-06

10.11999/JEIT160246

2016-03-17；改回日期：2016-08-18；

2016-10-09

庞菲菲 pang.1984@163.com

国家自然科学基金(61531015, 61501374, 61401499)，国家重点实验室基金(9140C230310150C23102)

The National Natural Science Foundation of China (61531015, 61501374, 61401499), The National Laboratory Foundation of China (9140C230310150C23102)