求解多旅行商问题的改进分组遗传算法
王勇臻 陈 燕 于莹莹
求解多旅行商问题的改进分组遗传算法
王勇臻*陈 燕 于莹莹
(大连海事大学交通运输管理学院 大连 116026)
该文针对总路径长度最小的多旅行商问题,提出一种改进分组遗传算法。在该算法中,设计了一种有序分组编码,采用新编码方式的个体与多旅行商问题有效解之间具有一一对应的关系。为了减少算法的运行时间,根据编码的特点构造了一种快速交叉算子。同时,结合贪婪算法和2-opt算法设计了一种新的局部搜索算子,以提高算法的收敛精度。实验结果分析表明,所提算法能够有效地解决多旅行商问题,具有可靠的全局收敛性,较高的计算效率。
分组遗传算法;多旅行商问题;编码;2-opt算法
1 引言
多旅行商问题(Multiple Traveling Salesman Problem, MTSP)是对经典旅行商问题(TSP)的推广,即给定个城市,个旅行商从同一(或不同)城市出发,分别走一条旅行路线,使得每个城市有且仅有一个旅行商经过(除出发城市),同时花费最小[1,2]。相较于TSP, MTSP具有更广泛的工程背景,如车辆路径规划[3]、应急物资配送[4]、无人机覆盖搜索[5]和不合格品控制[6]等,已被证明属于NP-hard问题。所以,如何快速、有效地解决MTSP具有很高的实际应用价值。
MTSP本质上属于分组问题,其求解过程包含了城市的分组优化以及组内遍历次序优化两个环节[7]。因此,相应的启发式算法大多计算复杂,并且过于依赖问题本身的特征,容易发生早熟收敛[1,8]。近年来,人们从生物机理中得到启发,提出了多种进化算法应用于MTSP,如遗传算法[9,10]、蚁群算法[11,12]、蜂群算法[13]和杂草入侵算法[14]。而编码方式作为进化算法的核心,直接影响着MTSP的求解性能,常见的有单染色体、双染色体和组合染色体3种编码[4,9]。然而,这些编码方式将两个优化环节融合在一起,不但使得进化算子通常难以设计,而且算法运行过程中容易产生大量的冗余解[9,10]。随着研究的深入,文献[9]提出了一种分组遗传算法(GGA-SS)用于求解MTSP,其基本思想是先将各旅行商的路径编码为个组,然后按照一定规则对组执行交叉、变异操作,计算结果优于早前算法。在此基础之上,文献[14]通过借鉴不同的生物智能,分别提出了3种群体进化算法(ABCFC, ABCVC和IWO),并且在多数实例上得到了目前最优的计算结果。但是,上述算法仍然存在两类问题:解空间存在冗余,以及缺乏有效的进化算子。
本文提出了一种改进分组遗传算法(IGGA- SS),设计了一种有序分组编码,将解空间进一步缩小了倍,并基于该编码构造了一种快速交叉算子,以减少算法的运行时间。同时,结合贪婪算法和2-opt算法设计了一种新的局部搜索算子,以进一步提高算法的收敛精度。实验结果分析表明,所提算法可以有效地解决MTSP,计算结果比目前同类算法给出的结果更优。

图1 GGA-SS编码示意图
2 GGA-SS求解MTSP
2.1 GGA-SS核心步骤
(2)交叉算子:GGA-SS采用一种两阶段交叉算子:
阶段1:从两个父代中随机选择一个,根据式(1)计算各组的,选择值最大的组并复制给子代。

阶段2:将阶段1中未分配的城市逐个插入到子代中,且保证每次插入都使得总路径长度增加最少。
(5)稳态保留:新生成的子代与当前种群进行比较,若唯一则替换当前最差个体,否则丢弃该子代。
2.2 GGA-SS存在的问题
通过分析GGA-SS主要计算过程可知,其存在3个问题:
(1)编码不考虑组的排列,存在冗余。
(3)阶段2本质上是贪婪算法,虽然在一定程度上能够得到满意解,但是随着问题规模的增大容易陷入局部极值。
3 IGGA-SS求解MTSP
3.1有序分组编码
由于GGA-SS编码不考虑组的排列,以图1为例,考虑如下编码方案:
{{4,7,10}, {6,1,3,11}, {12,5,2,8,9}},
{{4,7,10}, {12,5,2,8,9}, {6,1,3,11}},
{{6,1,3,11}, {4,7,10}, {12,5,2,8,9}},
{{6,1,3,11}, {12,5,2,8,9}, {4,7,10}},
{{12,5,2,8,9}, {4,7,10}, {6,1,3,11}},
{{12,5,2,8,9}, {6,1,3,11}, {4,7,10}}
对于MTSP,组本身所代表的旅行商没有任何意义,以上6个编码表达了同一个MTSP有效解。为了避免这种冗余,本文提出一种有序分组编码。上述例子中,假设3个组{4,7,10}, {12,5,2,8,9}和{6,1,3,11}的路径长度分别是100, 110和120,计算可得,和。反映了一个组属于最优解的可能性,越小则其属于最优解的概率越大[9]。然后将3个组按照进行升序排列,则{{12,5,2,8,9}, {6,1,3,11}, {4,7,10}}是有序分组编码后的唯一个体。
显然,有序分组编码的个体与MTSP有效解之间是一一对应的关系,其解空间大小是,较GGA-SS编码缩小了倍,有利于减小算法的复杂度,对大规模MTSP的求解具有重要意义。
3.2快速交叉算子(阶段1)
图2是快速交叉算子示意图。可见,该算子并未反复计算父代中各组的,提高了算法的计算效率。同时,该算子可以有效地保留父代中的部分分组,而基于有序分组编码,使得更具潜力的组优先得到保留。对于该阶段未分配的城市,将通过3.3节的局部搜索算子(阶段2)进行处理。
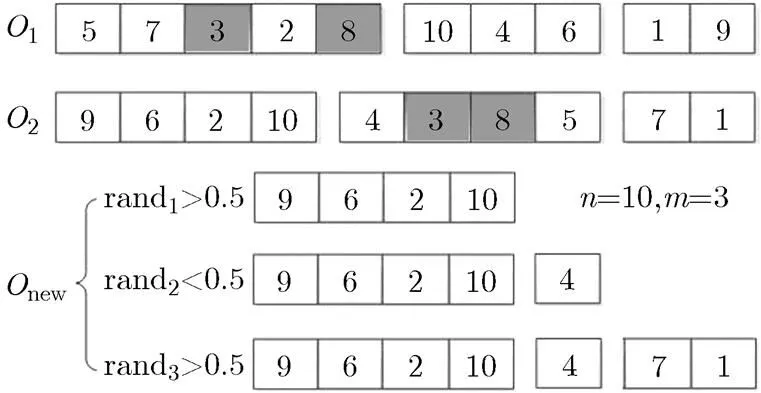
图2 快速交叉算子示意图

图3 2-opt算法示意图
3.3局部搜索算子(阶段2)
为了克服贪婪算法容易早熟收敛的缺陷,本文通过结合2-opt算法来引入新的信息,以维持种群的多样性,提出一种新的局部搜索算子,具体过程如下:
该算子既结合贪婪算法和2-opt算法来提高收敛精度,又引入了随机性保证种群不早熟收敛,平衡了算法的开发性和探索性。
3.4算法描述
在GGA-SS主要计算过程基础之上,下面给出IGGA-SS的求解步骤:
步骤1 算法和问题参数初始化;
步骤4 执行快速交叉算子,转步骤6;
步骤5 执行变异算子;
步骤6 执行局部搜索算子;
3.5时间复杂度分析
(3)计算各组的r并排序的时间复杂度。
综上所述,IGGA-SS迭代一次的时间复杂度为

4 实验结果与分析
本文采用Java语言编写程序实现算法,并在一台配置为Inter(R) Core(TM) i7-3770 CPU @3.40 GHz的PC上运行程序。参考文献[9,14]的做法,使用TSPLIB中距离对称的实例(设置不同的旅行商数目)进行数值实验。
为了便于控制选择压力,本文采用等级选择方法选取父代[17],如式(2),式(3)所示。其中,表示种群中第个个体被选中的概率,表示选择压力,,越大则选中最优个体的概率越大。

(3)
4.1参数设置及其影响
(3)选择压力SP从小到大取1.2~1.8,间隔为0.2;同样,偏好阈值取0.35~0.65,间隔为0.10。
表1参数水平

参数水平1水平2水平3水平4 SP1.21.41.61.8 pc0.60.70.80.9 pcp0.750.80.850.9 pd0.350.450.550.65
表2正交表和AVG统计(m)

NoSPpcpcppdAVG 1111123340.69 2122223450.00 3133323417.98 4144423327.05 5212323381.95 6221423506.34 7234123349.79 8243223428.10 9313423417.27 10324323410.60 11331223360.12 12342123394.59 13414223457.01 14423123342.49 15432423459.94 16441323540.87
表3各参数响应值(m)

水平SPpcpcppd 123383.9323399.2323437.0123356.89 223416.5423427.3623421.6223423.81 323395.6523396.9623401.4623437.85 423450.0823422.6523386.1123427.65 极差66.1530.4050.8980.96 等级2431
4.2算法性能分析
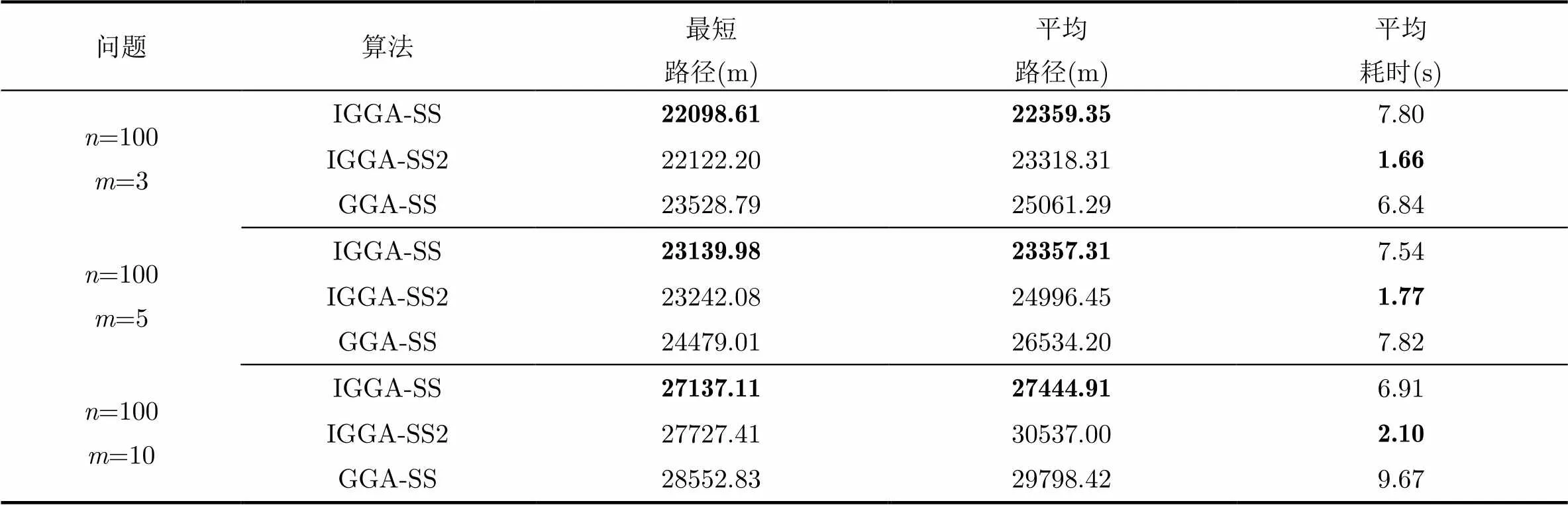
表4 3种算法20次独立运行结果统计
综合表4,图5和图6分析,可得出如下结论:
(1)对比GGA-SS和IGGA-SS2可知,快速交叉算子可以大幅度减少算法的耗时,计算可得IGGA-SS2相较于GGA-SS耗时减少了75.73%~ 78.28%,并且随着的增大其差距单调递增。但是,由于该算子不重新计算父代中各组的,将会影响各组保留的优先次序,随着的增大其收敛精度下降比较明显。
进一步地,由3.5节可知:交叉算子执行过程中,两者除了首次计算的耗时相同之外,GGA-SS反复计算的时间复杂度为其中,。易知,随着,,或者,亦或,的增大,这部分耗时累积将单调递增。在本文参数设置下,两者耗时差距已达到75%以上。
(2)对比IGGA-SS和IGGA-SS2可知,局部搜索算子可以进一步改善算法的收敛精度,计算可得IGGA-SS相较于IGGA-SS2收敛精度提高了4.11%~10.13%,并且随着的增大其差距单调递增,同时,两者耗时差距则单调递减。
(3)对比IGGA-SS和GGA-SS可知,本文所做改进可以有效地提高算法的收敛精度、减少算法的耗时。计算可得IGGA-SS相较于GGA-SS收敛精度提高了7.90%~11.97%。同时,随着的增大IGGA-SS耗时单调递减,除了之外(14.04%), IGGA-SS耗时均少于GGA-SS(3.58%和28.54%)。
4.3与知名算法的对比分析
为了更好地验证IGGA-SS求解MTSP的性能,引进目前最优秀算法:两种蜂群算法ABCFC, ABCVC和杂草入侵算法IWO作为比较对象[14],需要说明的是,这3种算法都是GGA-SS的变体。选取eil101, ch150()和kroB200()进行数值实验。设定为100,为1000,其余参数取自4.1节,所对比算法参数取自文献[14], 4种算法在每组实验上独立运行20次,结果如表5所示。可知,IGGA-SS在全部10组实验上均获得了4种算法中最好的结果,并且耗时最少。
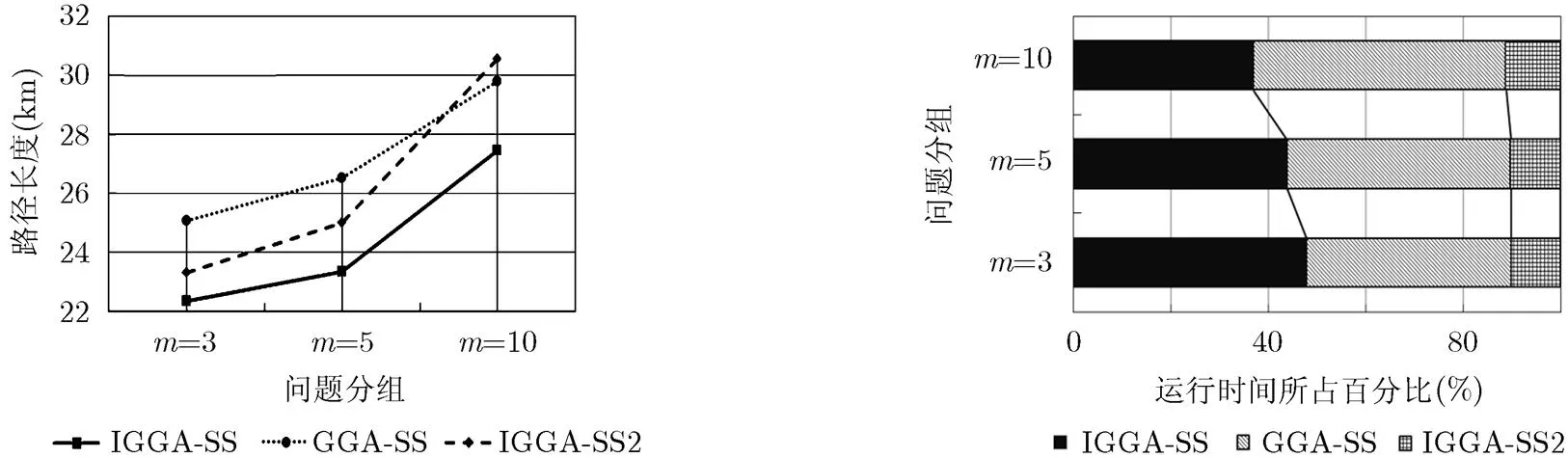
图5 m对3种算法收敛精度的影响 图6 m对3种算法耗时的影响

表5 4种算法20次独立运行结果统计
为了检验4种算法计算结果的差异在统计上是否显著,本文进行了单因素方差分析[19]。表6是4种算法的计算差异性对比,其中分别表示行所代表算法计算结果劣于、无区别和优于列所代表算法。从表6可知,IGGA-SS在全部10组实验上计算结果均优于ABCFC和ABCVC,在9组实验上计算结果优于IWO,整体性能最优;IWO整体性能仅次于IGGA-SS;而ABCFC与ABCVC整体性能相近。
从表5中4种算法耗时对比可见,IGGA-SS的耗时远少于其余3种算法,计算可得IGGA-SS相较于ABCFC, ABCVC与IWO耗时分别减少了61.77%~70.67%, 57.05%~67.91%和79.49%~ 84.93%。由3.5节与文献[14]可知,4种算法迭代一次的时间复杂度均为(·(变异算子+子代保留)),且均取1000。同时,(变异算子)的最高次幂都是的2次幂,且(变异算子)(子代保留),因此耗时差距主要源于取值不同。对比可知,IGGA-SS中取100,而ABCFC, ABCVC和IWO分别取250, 250和300,远大于IGGA-SS。这也说明,在种群规模较小的情况下,IGGA-SS依然可以得到比其余3种算法更高的收敛精度。
图7是4种算法收敛曲线对比。可知,IGGA-SS的收敛速度最快,几乎是垂直收敛,并且迭代过程中始终处于其余3种算法的下方。ABCFC在迭代前期收敛速度较快,然而容易早熟收敛。IWO和ABCVC虽然没有陷入局部极值,但是收敛速度与IGGA-SS存在明显差距。

表6 4种算法的计算差异性对比
综上所述,IGGA-SS在收敛速度、精度以及耗时方面均优于所对比的3种算法。
5 结束语
本文提出了一种改进分组遗传算法,用于求解总路径长度最小的MTSP。实验结果分析表明,IGGA-SS具有比最新用于解决该问题的ABCFC, ABCVC和IWO更优的性能。今后工作仍需进行更多的数值实验和对算法的效率作进一步改进,并将所提算法应用于解决港口自动调度这类大规模MTSP。
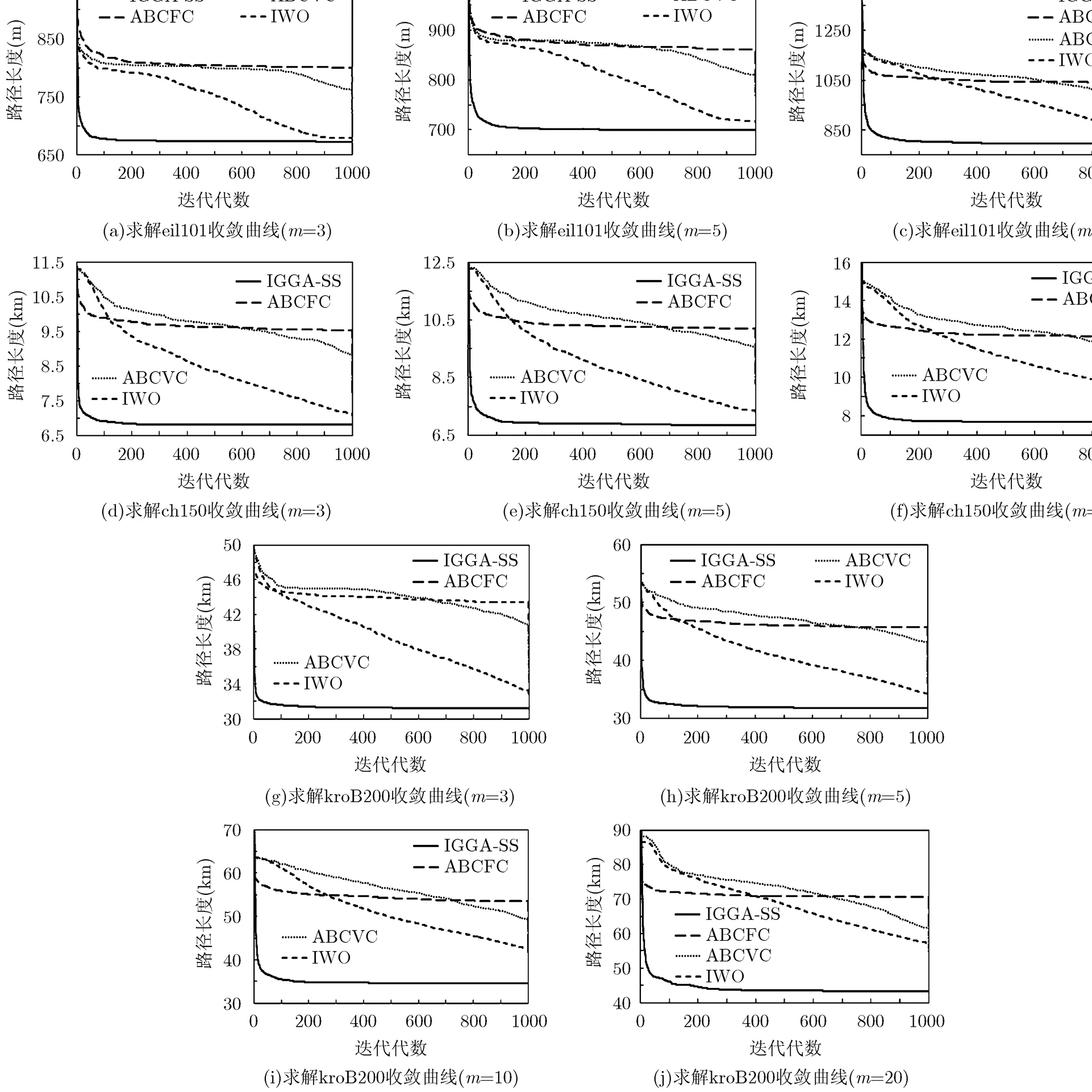
图7 4种算法收敛曲线对比
[1] SOYLU B. A general variable neighborhood search heuristic for multiple traveling salesmen problem[J].&, 2015, 90(11): 390-401. doi: 10.1016/j.cie.2015.10.010.
[2] KOTA L and JARMAI K. Mathematical modeling of multiple tour multiple traveling salesman problem using evolutionary programming[J]., 2015, 39(12): 3410-3433. doi: 10.1016/j.apm. 2014.11.043.
[3] 谢秉磊, 李颖, 刘敏. 带临时补充点的融雪剂撒布车辆路径问题[J]. 系统工程理论与实践, 2014, 34(6): 1593-1598. doi: 10.12011/1000-6788(2014)6-1593.
XIE Binglei, LI Ying, and LIU Min. Vehicle routing problem with temporary supplementary points for spreading deicing salt[J].&, 2014, 34(6): 1593-1598. doi: 10.12011/1000-6788(2014)6-1593.
[4] 刘明, 张培勇. 求解多旅行商问题的新混合遗传算法: 以应急物资配送为例[J]. 系统管理学报, 2014, 23(2): 247-254.
LIU Ming and ZHANG Peiyong. New hybrid genetic algorithm for solving the multiple traveling salesman problem: An example of distribution of emergence materials[J].&, 2014, 23(2): 247-254.
[5] ANN S, KIM Y, and AHN J. Area allocation algorithm for multiple UAVs area coverage based on clustering and graph method[J]., 2015, 48(9): 204-209. doi: 10.1016/j.ifacol.2015.08.084.
[6] KIRALY A, CHRISTIDOU M, CHOVAN T,. Minimization of off-grade production in multi-site multi-product plants by solving multiple traveling salesman problem[J]., 2016, 111: 253-261. doi: 10.1016/j.jclepro.2015.05.036.
[7] KASHAN A H, AKBARI A A, and OSTADI B. Grouping evolution strategies: an effective approach for grouping problems[J]., 2015, 39(9): 2703-2720. doi: 10.1016/j.apm.2014.11.001.
[8] BEKTAS T. The multiple traveling salesman problem: An overview of formulations and solution procedures[J]., 2006, 34(3): 209-219. doi: 10.1016/j.omega.2004.10.004.
[9] SINGH A and BAGHEL A S. A new grouping genetic algorithm approach to the multiple traveling salesperson problem[J]., 2009, 13(1): 95-101. doi: 10.1007/s00500-008-0312-1.
[10] YUAN S, SKINNER B, HUANG S,. A new crossover approach for solving the multiple travelling salesmen problem using genetic algorithms[J]., 2013, 228(1): 72-82. doi: 10.1016/j.ejor.2013.01.043.
[11] LIU W, LI S, ZHAO F,. An ant colony optimization algorithm for the multiple traveling salesmen problem[C]. Proceedings of IEEE Conference on Industrial Electronics and Applications, ICIEA, Xi’an, China, 2009: 1533-1537. doi: 10.1109/ ICIEA.2009.5138451.
[12] NECULA R, BREABAN M, and RASCHIP M. Performance Evaluation of Ant Colony Systems for the Single-depot Multiple Traveling Salesman Problem[M]. Springer International Publishing, 2015: 257-268. doi: 10.1007/ 978-3-319-19644-2_22.
[13] XUE M, WANG T, and MAO S. Double evolutsional artificial bee colony algorithm for multiple traveling salesman problem[C]. Preoeedings of MATEC Web of Conferences, EDP Sciences, 2016: 44. doi: 10.1051/ matecconf/20164402025.
[14] VENKATESH P and SINGH A. Two metaheuristic approaches for the multiple traveling salesperson problem[J]., 2015, 26: 74-89. doi: 10.1016/ j.asoc.2014.09.029.
[15] 韩丽霞, 王宇平, 兰绍江. 基于有序划分编码的图着色算法[J]. 电子学报, 2010, 38(1): 146-150.
HAN Lixia, WANG Yuping, and LAN Shaojiang. Graph coloring algorithm based on ordered partition encoding[J]., 2010, 38(1): 146-150.
[16] HELSGAUN K. General k-opt submoves for the Lin–Kernighan TSP heuristic[J]., 2009, 1(2/3): 119-163. doi: 10.1007/s12532- 009-0004-6.
[17] ALIJLA B O, WONG L P, LIM C P,. A modified intelligent water drops algorithm and its application to optimization problems[J]., 2014, 41: 6555-6569. doi: 10.1016/j.eswa.2014.05.010.
[18] WANG S, WANG L, LIU M,. An effective estimation of distribution algorithm for solving the distributed permutation flow-shop scheduling problem[J]., 2013, 145(1): 387-396. doi: 10.1016/j.ijpe.2013.05.004.
[19] 王军强, 郭银洲, 崔福东, 等. 基于多样性增强的自适应遗传算法的开放式车间调度优化[J]. 计算机集成制造系统, 2014, 20(10): 2479-2493. doi: 10.13196/j.cims201410016.
WANG Junqiang, GUO Yinzhou, CUI Fudong,. Diversity enhancement-based adaptive genetic algorithm for open-shop scheduling problem[J]., 2014, 20(10): 2479-2493. doi: 10.13196/j.cims201410016.
王勇臻: 男,1990年生,博士生,研究方向为智能计算、数据挖掘等.
陈 燕: 女,1952年生,教授,研究方向为管理科学与决策、知识管理、数据仓库与数据挖掘等.
于莹莹: 女,1987年生,博士生,研究方向为数据挖掘、信息检索等.
Improved Grouping Genetic Algorithm for Solving Multiple Traveling Salesman Problem
WANG Yongzhen CHEN Yan YU Yingying
(,,116026,)
In order to solve the total-path-shortest Multiple Traveling Salesman Problem (MTSP), an improved grouping genetic algorithm is proposed. This algorithm employs a new encoding scheme called ordered grouping encoding, which makes the adjusted individuals corresponding one by one to valid solutions of MTSP. According to the features of the encoding scheme, a fast crossover operator is constructed for the sake of reducing the running time of the algorithm. For enhancing its local search ability, the algorithm combines the greedy algorithm and the 2-opt algorithm to design a new local search operator. The comparison of results shows that the proposed algorithm can solve MTSP effectively and has an excellent search performance no matter in computing efficiency or convergence precision.
Grouping Genetic Algorithm (GGA); Multiple Traveling Salesman Problem (MTSP); Encoding; 2-opt algorithm
TP18
A
1009-5896(2017)01-0198-08
10.11999/JEIT160211
2016-03-07;改回日期:2016-07-22;
2016-10-09
王勇臻 kuadmu@163.com
国家科技支撑计划(2014BAH24F04),国家自然科学基金(71271034)
The National Key Technology Research and Development Program of the Ministry of Science and Technology of China (2014BAH24F04), The National Natural Science Foundation of China (71271034)

