一种特殊的多米诺扩缩运算

刘小青 许 进



一种特殊的多米诺扩缩运算

刘小青 许 进*

(北京大学信息科学技术学院 北京 100871);(北京大学高可信软件技术教育部重点实验室 北京 100871)

该文提出一种称为334扩缩运算的多米诺扩缩运算。使用该运算构造了一类特殊的极大平面图——334-型极大平面图，证明了该类图均为树型2-色不变圈着色，且每个-阶334-型极大平面图恰有个2-色不变圈着色及个树着色。证明了该运算可用于构造纯树着色极大平面图，并提出猜想：若极大平面图是纯树(纯圈，混合)着色，则对实施334扩(缩)轮运算后，所得之图仍是纯树(纯圈，混合)着色。

半封漏斗；树型2-色不变圈着色；纯树着色；334扩轮运算

1 引言

文献[6,7]对平面图的着色类型进行了研究，将着色分为树着色和圈着色，依据着色类型将4-色平面图分为3类：纯树着色型、纯圈着色型和混合着色型，并提出了纯树着色猜想“一个平面图是纯树着色图当且仅当它是正二十面体或哑铃极大平面图”，若该猜想成立，则著名的已有43年历史的唯一4-色平面图猜想成立。文献[13]定义了一类特殊的圈着色2-色不变圈着色，在此基础上，将4-色非Kempe平面图的Kempe等价类分为树型，圈型和循环圈型，这也是非Kempe平面图存在的根源。若一个-色图的都有-着色构成一个Kempe等价类，则称该图为Kempe图。

本文给出了一种构造具有相同着色类型的极大平面图类的方法，包含334扩轮运算和334缩轮运算。具体安排如下：第2节给出了334扩轮运算及334缩轮运算的定义；第3节基于334扩缩运算研究了一类树型2-色不变圈着色极大平面图334-型极大平面图的基本性质；第4节讨论了334-型极大平面图的着色性质；第5节给出了用334扩轮运算构造纯树着色极大平面图的方法。

文中未给出的相关定义、记号与理论参见文献[6,13-15]。

图1 漏斗与45-型半封漏斗子图

2 334扩缩运算

把图1(a)中所示的图称为漏斗，其中度数为1的顶点称为漏顶；度数为3的顶点称为漏腰；2个度数为2的顶点称为漏底。若一个图的顶点导出子图是漏斗，则该子图称为漏斗子图。334扩缩运算本质上是一种多米诺扩缩运算[14]，其中，334扩轮运算包含2次扩3-轮运算以及一次扩4-轮运算；334缩轮运算包含2次缩3-轮运算以及一次缩4-轮运算。设是一个极大平面图，图是一个标号如图1(b)所示的半封漏斗。若是的一个子图，且，，则称是的一个45-型半封漏斗子图，简称为45-型子图。

334扩轮运算的对象图是极大平面图中的45-型子图。334扩轮运算，记作，是指按照如下步骤，将的一个45-型子图(如图1(b)所示)变成图2(a)~2(d)中最右边所示构形的过程：

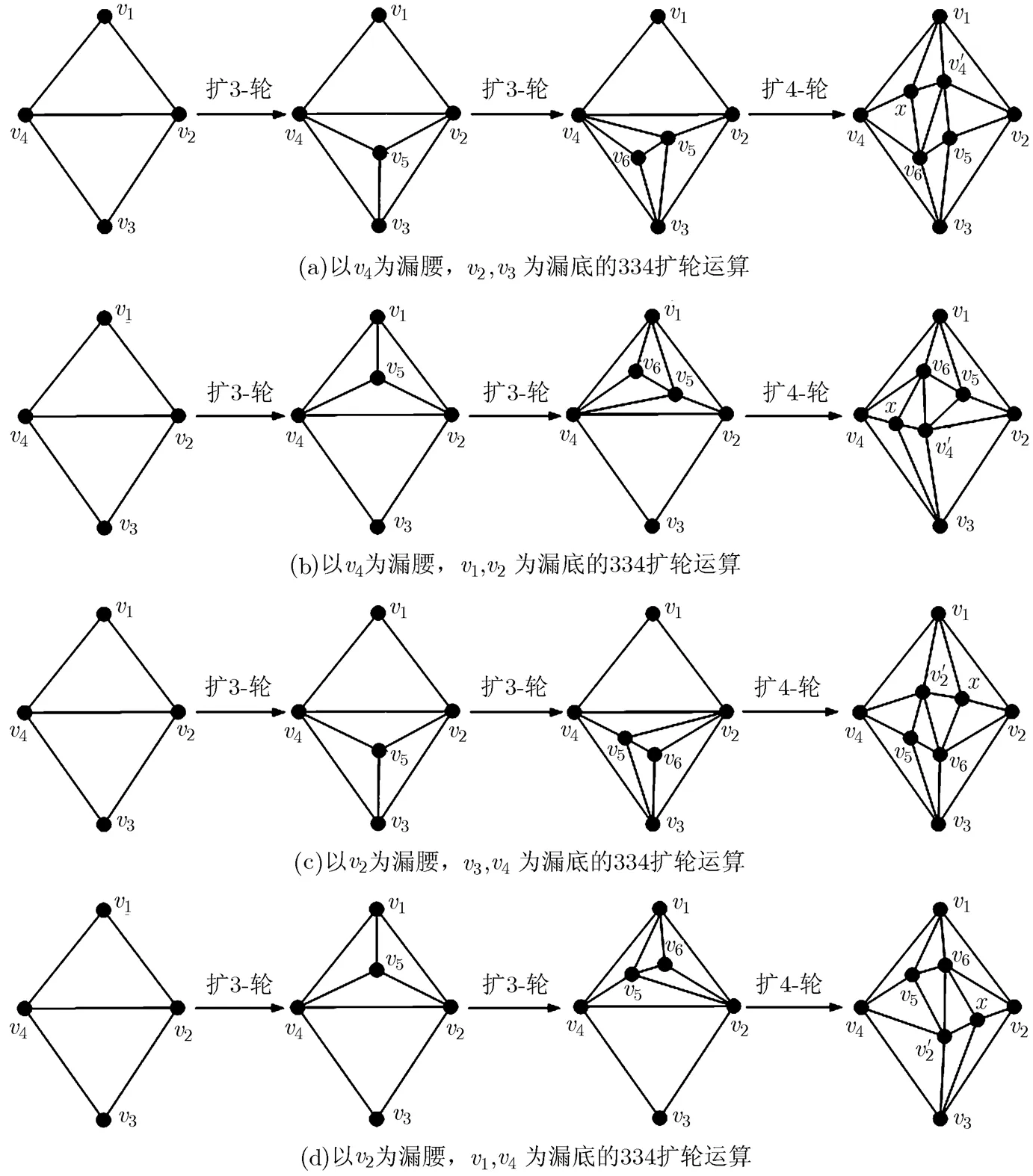
图2 选择不同漏腰和漏底的334扩轮运算过程示意图

(2)在图2(a)与图2(d)中，2个最右边构形的区别仅是构形的内部顶点标号不同，若对一个极大平面图的同一个45-型子图分别实施如图2(a)和图2(d)所示过程的334扩轮运算，则得到2个相同的极大平面图，故视这2个构形是相同的；同理，图2(b)与图2(c)中2个最右边的构形是相同的。

图3(a)，图3(d)，图3(e)，图3(h)中最右边构形的区别仅是构形的顶点标号方式不同，对一个极大平面图的同一个334子图分别实施如图3(a)，图3(d)，图3(e)，图3(h)所示过程的334缩轮运算，则得到4个相同的极大平面图，故视图3(a)，图3(d)，图3(e)，图3(h)中最右边的构形是相同的；同理，图3(b)，图 3(c)，图3(f)，图3(g)中最右边的构形是相同的。

图3 选择不同被收缩点对的334缩轮运算过程示意图

3 334-型极大平面图

3.1334-型极大平面图及构造

图4所示的图是阶数最小的最小度为4且含45-型子图的极大平面图，称为8-阶334-型极大平面图，记作。

3.2 334-型极大平面图的基本性质

由定理2可推出下述结论：

证明 由前面讨论知，任意334子图仅有一个与之不相同的334子图。

图4 8-阶334-型极大平面图 图5 2个12-阶334-型极大平面图

若将图5(a)中上方的334子图替换为与之不相同的334子图，如图6(a)所示，则得到一个与图5(b)同构的图；若将图5(a)中下方的334子图替换为与之不相同的334子图，如图6(b)所示，则得到一个与图5(b)同构的图。若将图5(b)中的任意一个334子图替换为与之不相同的334子图，则得到与图5(a)同构的图。故时结论成立。

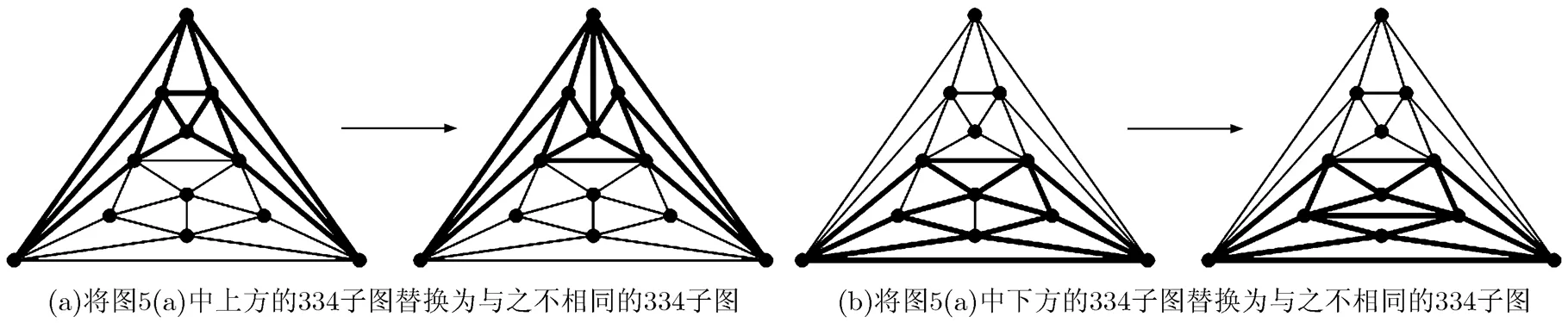
图6 定理3证明示意图

由推论1和定理3，可直接推出下述结论：

定理4 每个334-型极大平面图恰有4个4度顶点。

8-阶334-型极大平面图为如图4所示的图，其度序列为44445555，结论成立。12-阶334-型极大平面图共有2个，分别如图5(a)，图5(b)所示，它们均恰含4个4度顶点，结论成立。

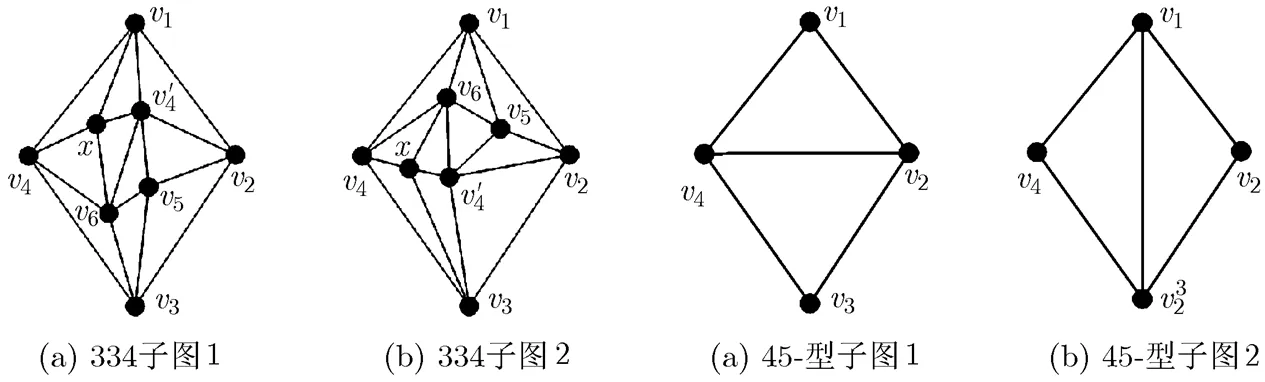
图7 2个不相同的334子图　　　　　　图8 2个不相同的45-型子图

4 334-型极大平面图着色性质

在扩4-轮运算过程中，对象子图2-长路的内点被划开成为2个顶点，如图9所示，将该内点称为扩点，由划开产生的2个顶点称为扩点的拷贝顶点。类似，把扩5-轮运算对象子图的漏腰称为扩点，扩点被划开后产生的2个顶点称为扩点的拷贝顶点。

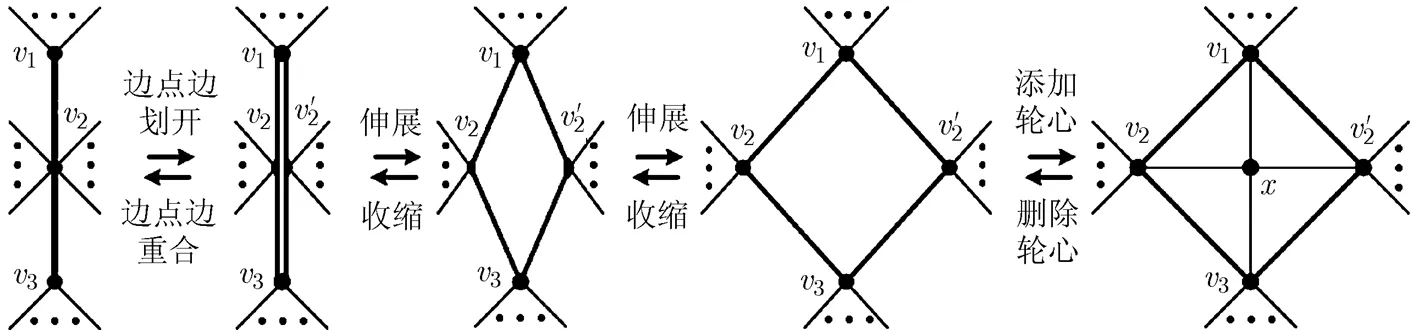
图9 扩缩4-轮运算的示意图

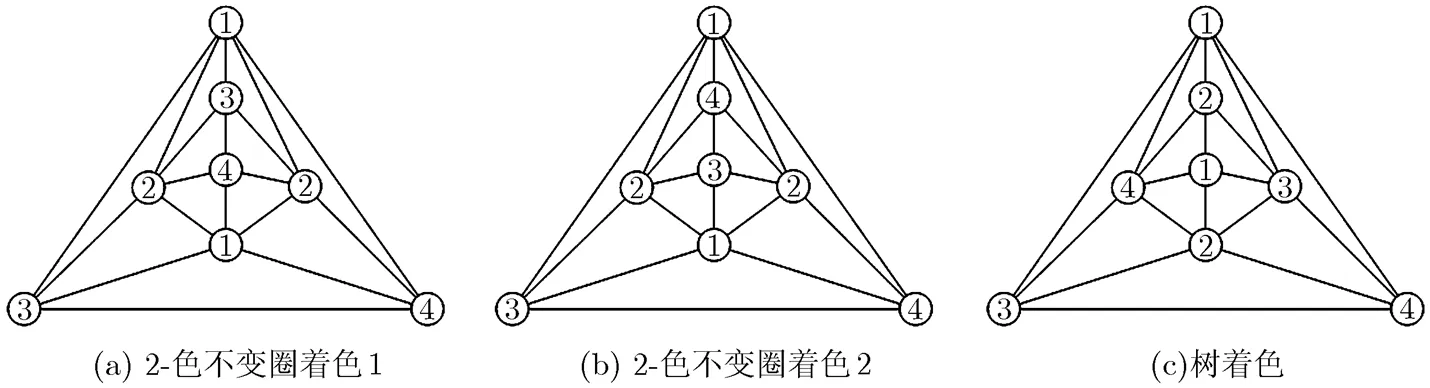
图10 的所有着色

定理5 每个334-型极大平面图均是树型2-色不变圈着色。

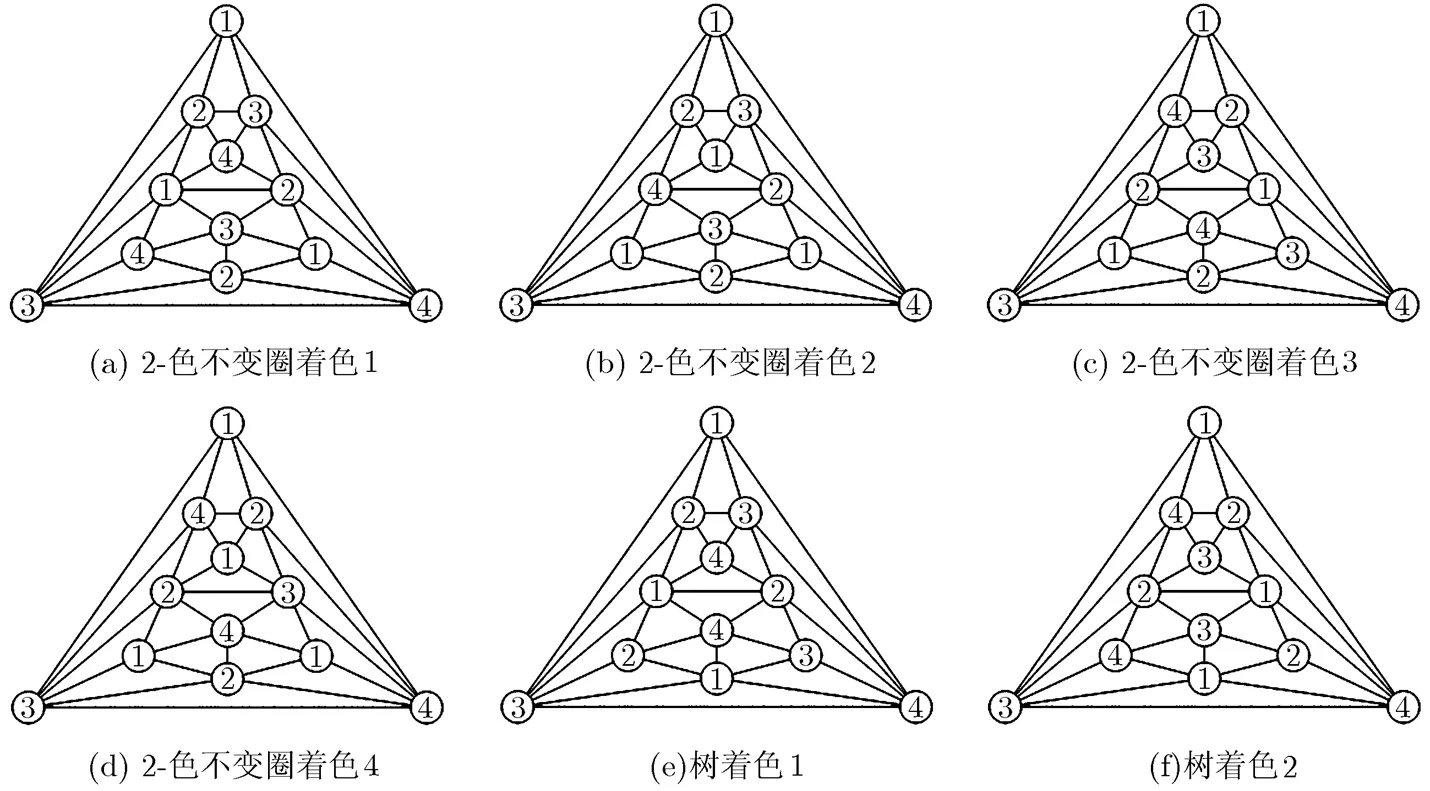
图11 的所有着色

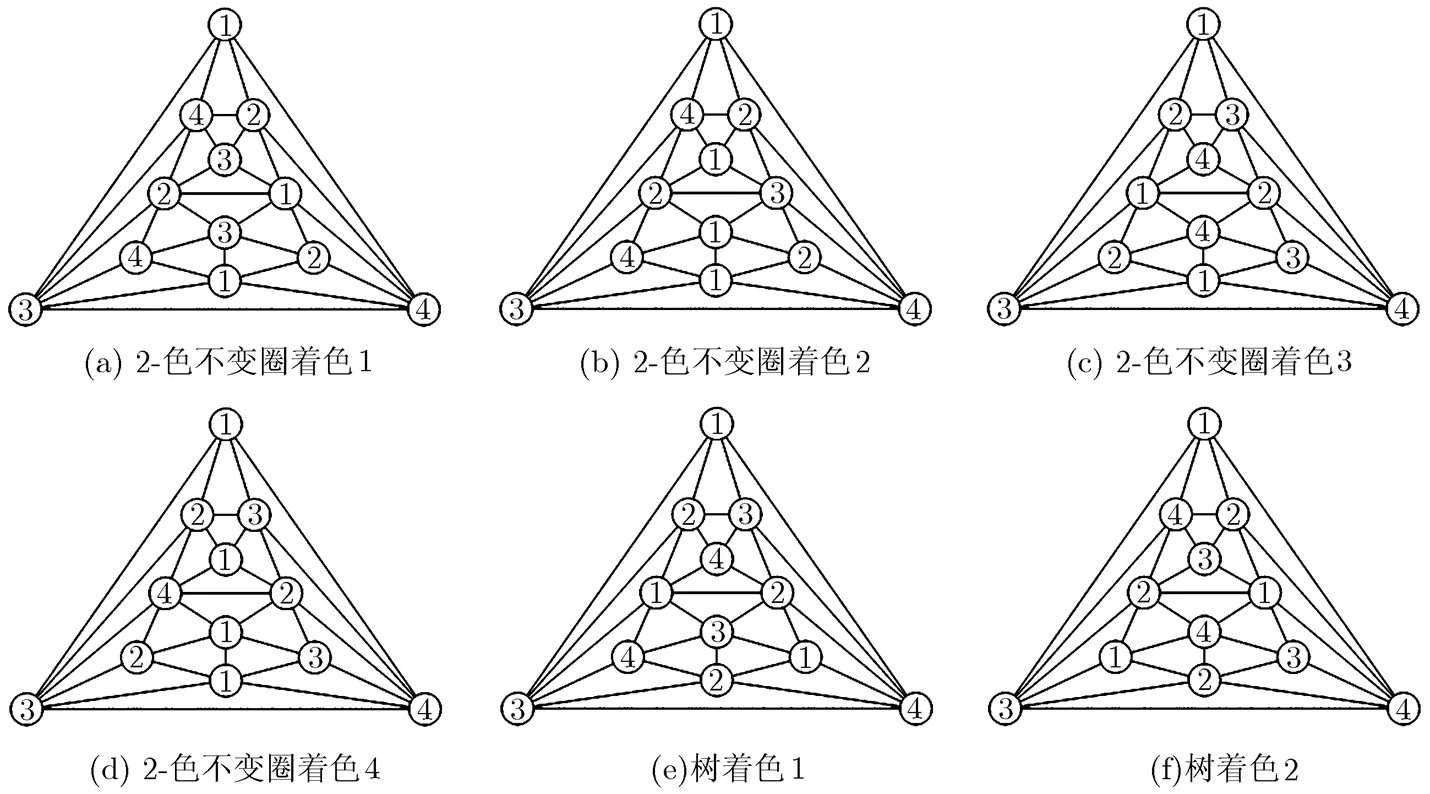
图12 的所有着色

证毕

5 构造纯树着色极大平面图

利用334扩轮运算，除了构造334-型极大平面图，还可以构造其它非常重要的图类，例如，纯树着色极大平面图。7至11阶最小度的极大平面图共有54个[14]，其中纯树着色的图只有1个[6,7]，记作，如图13(a)所示。共有3个45-型子图。对其中的任意一个45-型子图实施334扩轮运算，均得到如图13(b)所示的13-阶纯树着色极大平面图，记为。

由定理5知，从一个最小度为4的8-阶树型2-色不变圈着色极大平面图出发，实施任意次数的334扩轮运算后，所得之图均是树型2-色不变圈着色的；再由定理7知，从一个最小度为4的9-阶纯树着色极大平面图出发，实施任意次数的334扩轮运算后，所得之图也都是纯树着色的。基于这些结论，我们进一步提出如下猜想：

图13 和

6 结束语

本文给出了一种称为334扩缩运算的扩缩运算，它能够构造具有相同着色类型的4-色极大平面图。在后续工作中，我们将对文中给出的猜想予以论证，并进一步研究不同着色类型图所具有的特殊性质。

[1] MOHAR B. Kempe Equivalence of Colorings[M]. Graph Theory in Paris. Birkhäuser Basel, 2006: 287-297. doi: 10.1007/978-3-7643-7400-6_22.

[2] VERGNAS M L and MEYNIEL H. Kempe classes and the Hadwiger conjecture[J]., 1981, 31(1): 95-104. doi: 10.1016/S0095-8956(81) 80014-7.

[3] FEGHALI C, JOHNSON M, and PAULUSMA D. Kempe equivalence of colourings of cubic graphs[J]., 2015, 49: 243-249. doi: 10.1016/ j.endm.2015.06.034.

[4] MCDONALD J, MOHAR B, and SCHEIDE D. Kempe equivalence of edge-colorings in subcubic and subquartic graphs[J]., 2012, 70(2): 226-239. doi: 10.1002/jgt.20613.

[5] BELCASTRO S M and HAAS R. Counting edge-Kempe- equivalence classes for 3-edge-colored cubic graphs[J]., 2014, 325(13): 77-84. doi: 10.1016/ j.disc.2014.02.014.

[6] 许进. 极大平面图的结构与着色理论(3): 纯树着色与唯一4-色极大平面图猜想[J]. 电子与信息学报, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

XU J. Theory on structure and coloring of maximal planar graphs(3): Purely tree-colorable and uniquely 4-colorable maximal planar graph conjectures[J].&, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

[7] XU J, LI Z P, and ZHU E Q. On purely tree-colorable planar graphs[J]., 2016, 116(8): 532-536. doi: 10.1016/j.ipl.2016.03.011.

[8] GREENWELL D and KRONK H V. Uniquely line-colorable graphs[J]., 1973, 16(4): 525-529. doi: 10.4153/CMB-1973-086-2.

[9] THOMASON A G. Hamiltonian cycles and uniquely edge colourable graphs[J]., 1978, 3: 259-268. doi:10.1016/S0167-5060(08)70511-9.

[10] FIORINI S and WILSON R J. Edge colouring of graphs[J]., 1977, 23(1): 237-239.

[11] FISK S. Geometric coloring theory[J]., 1977, 24(3): 298-340. doi: 10.1016/0001-8708 (77)90061-5.

[12] TOMMY R J and BJARNE T. Graph Coloring Problems[M].New York: USA, John Wiley & Sons, Inc., 1994: 1-295.

XU J. Theory on structure and coloring of maximal planar graphs (4):-operations and Kempe equivalent classes[J].&, 2016, 38(7): 1557-1585. doi: 10.11999/JEIT160483.

[14] 许进. 极大平面图的结构与着色理论(2): 多米诺构形与扩缩运算[J]. 电子与信息学报, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT160224.

XU J. Theory on structure and coloring of maximal planar graphs(2): Domino configurations and extending-contracting operations[J].&, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT 160224.

[15] BONDY J A and MURTY U S R. Graph Theory[M]. New York: USA, Springer, 2008: 8-200.

刘小青： 女，1986年生，博士生，研究方向为图论与组合优化.

许 进： 男，1959年生，教授，研究方向为图论与组合优化、生物计算机、社交网络与信息安全等.

Special Type of Domino Extending-contracting Operations

LIU Xiaoqing XU Jin

(,,100871,);(,,100871,)

In this paper, a new domino extending-contracting operation, called 334 extending-contracting operation, is put forward, on the basis of which, it is proposed to construct a particular kind of graphs, i.e., 334-type maximal planar graphs, and proved that all those graphs are tree-type and 2-chromatic cycle-unchanged colored and every 334-type maximal planar graphs of orderhas exactly2-chromatic cycled-unchanged colorings andtree-colorings. Additionally, it is proved that an infinite family of purely tree-colored graphs can be generated by implementing a series of 334 extending-wheel operations, and conjectured that if a maximal planar graphis purely tree-colored (purely cycle-colored or impure-colored), then the graph obtained by implementing one 334 extending-wheel (contracting-wheel) operation onis still purely tree-colored (purely cycle-colored or impure-colored).

Semi-funnels; Tree-type and 2-chromatic cycle-unchanged colored; Purely tree-colored; 334 extending- wheel operations

O157.5

A

1009-5896(2017)01-0221-10

10.11999/JEIT160886

2016-08-29；改回日期：2016-12-06；

2016-12-14

许进 jxu@pku.edu.cn

国家973计划项目(2013CB329600)，国家自然科学基金(61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

The National 973 Program of China (2013CB329600), The National Natural Science Foundation of China (61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)