基于辅助符号的非线性自干扰抵消算法及其简化实现

王 丹 黄开枝 李云洲



基于辅助符号的非线性自干扰抵消算法及其简化实现

王 丹*①②黄开枝①李云洲②

①(解放军信息工程大学国家数字交换系统工程技术研究中心 郑州 450002);②(清华大学信息技术研究院无线与移动通信技术研究中心 北京 100084)

同频同时全双工是第5代(5G)通信关键技术之一，数字自干扰抵消算法是其重要研究方向。针对非线性数字自干扰抵消算法中，失真系数估计受到自干扰信道估计误差的影响这一问题，该文提出一种基于辅助符号的非线性自干扰抵消算法，通过对辅助符号做自干扰抵消，将信道估计符号的失真误差映射到其抵消结果中并提取出来，从中估计失真系数。接着针对算法开销问题提出一种简化实现方案。仿真结果显示，接收自干扰信号为-5 dBm时，算法可将自干扰非线性失真分量抵消至约-100 dBm，且性能随接收自干扰功率降低而提高。

5G；同频同时全双工；数字自干扰抵消；非线性失真估计

1 引言

同频同时全双工(以下简称全双工)是第5代通信(5G)提出的关键技术之一，是指通信设备利用同一频段同时进行信号收、发，提高了频谱利用率。全双工的核心技术为自干扰抵消[5]，一般分为天线域[6,7]、模拟域[8,9]和数字域[10]3级。本文的研究对象为数字自干扰抵消。

由于硬件电路总会带来噪声、失真畸变等，实际中自干扰信号不可能达到理想的消除[11]。研究表明，自干扰信号使接收链路处于饱和状态，故失真噪声对节点希望接收的信号构成强干扰[12]，一方面表现为被抵消信号的残留噪声，另一方面造成自干扰信道估计误差，降低数字抵消的准确性。非线性自干扰抵消算法在正常自干扰抵消之前添加3个步骤：失真估计，失真还原，失真补偿，来消除这一影响。在这一过程中，需要估计自干扰信道和失真系数两个参数。然而，非线性失真给信道估计造成误差，后者又会影响失真系数的估计，两者相互耦合。文献[16]提出一种自干扰信道和失真系数联合估计算法，通过迭代消除二者的耦合作用。然而，算法只把信道估计符号的失真视为一般噪声，而未将其剥离出来，故迭代中每一步失真系数估计，仍会受到前一步结果的误差影响，并没有从本质上解耦信道估计和失真系数。

针对这一问题，本文提出了一种基于辅助符号的非线性自干扰抵消算法。在前导码字段中设计一个辅助符号，把信道估计符号的非线性失真映射到该辅助符号的抵消结果中，解耦信道估计和失真系数估计。然后，估计出失真系数，按照非线性分量数学模型还原失真并补偿接收信号；最后，再对补偿后的信号做自干扰抵消。为了进一步提高算法普适性，降低通信开销，文中又提出了一种算法的简化实现方案。仿真结果显示，接收信号为20 dBm时，算法可将自干扰非线性失真分量降至约-100 dBm，且其性能随接收自干扰功率降低而提高。

2 非线性自干扰抵消模型

自干扰信号通过低噪声放大器(Low Noise Amplifier, LNA)时会产生各种高次非线性分量，其中次项的常系数定义为阶失真系数[17]。工程中通常以三阶输入交调截点(Input 3rd order intercept point)作为衡量器件线性度的指标，因此文献以三阶失真为主要研究对象。非线性分量残留在抵消结果中，降低了传统算法的信噪比性能。非线性自干扰抵消通过估计失真系数，还原非线性分量，对发生畸变的自干扰信号做线性化补偿后再进行抵消，来降低抵消残留噪声，提升信噪比性能。算法流程如图1所示。

图1 非线性自干扰抵消算法原理框图

目前，全双工研究普遍基于正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统；失真系数估计是全双工非线性自干扰抵消算法的核心环节。文献[16]针对OFDM全双工系统提出一种非线性自干扰抵消算法，对失真系数采取如下估计：对发生失真畸变的信号做自干扰抵消，认为抵消残余约等于被抵消信号的非线性失真分量，则LNA三阶失真系数与抵消残余之间存在关系：

上述估计方法的主要问题是约等号成立的条件太松，表现为：

针对以上问题，本文提出一种基于辅助符号的非线性失真抵消算法，设计一个辅助符号，通过对该符号做自干扰抵消，把映射到抵消结果中的信道估计符号失真提取出来，消除信道估计误差对失真系数估计的影响。在对辅助符号做自干扰抵消时，用发送链路末端取样代替传统的发送数字基带取样，来获得抵消参考信号[18]，消除其误差对失真系数估计的影响。

3 基于辅助符号的非线性自干扰抵消算法

基于辅助符号的非线性自干扰抵消算法通过设计辅助符号，并采用发送链路末端取样法[18]获取抵消参考信号，对其做自干扰抵消，把映射到抵消结果中的信道估计符号失真提取出来，解决抵消参考信号误差和信道估计误差对失真系数估计的影响。最后，用得到的失真系数还原非线性失真噪声，并对接收信号进行线性化补偿后，再做正常的自干扰抵消。算法包含以下4个部分：(1)失真映射与提取；(2)失真估计；(3)失真还原和补偿；(4)自干扰抵消。

3.1失真映射与提取

失真映射与提取是为了解决失真系数估计和信道估计的耦合问题。基本思路是将信道估计符号作为失真系数的一部分载体加以考虑。失真映射通过对辅助符号做自干扰抵消，获得信道估计失真误差，之后，通过失真提取，将其转化为独立的非线性失真，再从抵消结果估计非线性失真系数就可以摆脱自干扰信道估计误差的影响。

3.1.1辅助符号设计以802.11a物理帧格式为例，说明辅助符号的设计过程。802.11a的物理帧包括3个部分[19]：前导码(preamble)，信令域(SIGNAL)，以及数据域(DATA)。前导码由12个OFDM符号组成，首先是10个时长均为800 ns的重复的短训练序列，用于AGC、信号头检测、粗频率偏移估计及符号定位，然后是2个重复的长训练序列，每一个持续时长为一个OFDM符号的长度，再添加一半的符号用于循环前缀，总时长为，用于精频率偏移估计、信道估计。

为了达到提取信道估计失真的要求，辅助符号应满足以下3个条件：(1)包含全部非零子载波；(2)该符号时隙内全双工节点还未开始接收其他节点发来的信号，以免对失真系数造成干扰；(3)能从抵消结果中独立地提取出被抵消符号的非线性失真和信道估计符号的非线性失真。

为了满足条件(1)，则短训练序列符号不能用作辅助符号：根据802.11a的协议规定，短训练序列在映射为OFDM符号时只用了52个非零子载波中的12个[19]。为了满足条件(2)，则辅助符号不能设置在数据域中：为了保证自干扰信道的准确估计，一般假设前导码传送完毕启动全双工模式，因此数据域符号都混叠了节点希望接收的信号，这些信号对失真系数的估计构成噪声；为了满足条件(3)，则信道估计符号不能用作辅助符号：对信道估计符号本身做自干扰抵消时，其非线性失真既存在于被抵消信号中，也存在于信道估计误差中，前后相消，无法从抵消结果中估计失真系数。

综上，对帧格式改动程度最低的方案是在前导码域增加一个与信道估计符号完全一致的辅助符号，专门用于估计失真系数，如图2所示。辅助符号时长与信道估计序列符号相等，为。

图2 添加辅助符号的802.11a帧格式示意图

3.1.2失真映射 失真映射即对辅助符号做自干扰抵消，将信道估计符号中的失真误差映射到辅助符号的抵消残余中。本文采用发送链路末端取样法[18]获取抵消参考信号，来消除抵消参考信号误差对失真系数估计的影响，如图3所示，将发送链路末端信号耦合出一部分，通过有线链路直接下变频数字化，得到发送链路末端抵消参考信号，记为。

对辅助符号做自干扰抵消：

图3 获取发送末端抵消参考信号原理框图

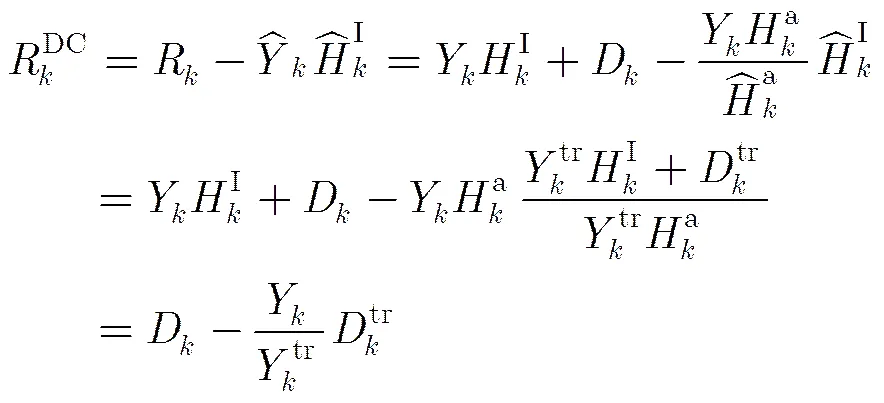
3.2失真估计

失真映射和提取完成了信道估计和失真系数估计的解耦。此时，根据非线性失真的数学模型，可直接从式(3)等号右侧提取出失真系数，再变形即可得到用辅助符号的抵消结果表示的失真系数估计。

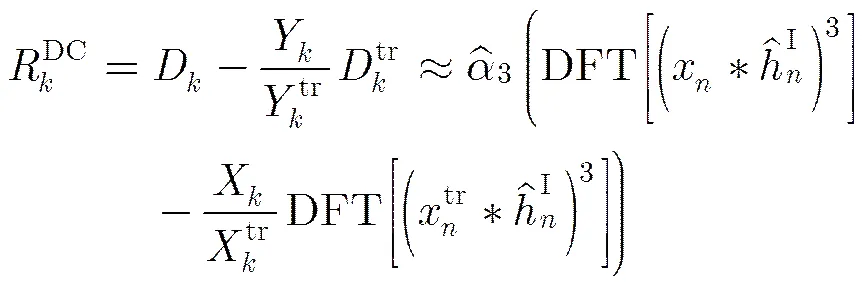
即

(5)

与文献[16]算法的失真系数估计式(1)相比，本文算法的失真系数估计中不再含有自干扰信道估计项，实现了信道估计和失真系数估计的解耦；分母中的3次项虽然含有信道估计，但其物理含义是自干扰信号的三阶失真，强度远小于主信号，因此可以忽略其中的误差。后文的仿真也说明了这一点。

3.3 失真还原与补偿

得到失真系数估计后，接收端按照非线性失真的数学模型[17]将其还原，得到还原非线性分量再与失真信号作差，消除叠加在接收自干扰信号中的非线性失真噪声，得到线性化的自干扰信号。失真还原与补偿分别表示为

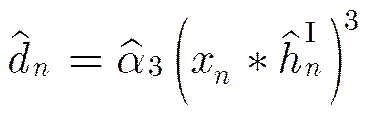
(7)

3.4自干扰抵消

线性化后的信号消除了失真噪声的影响，即可用传统的信道估计-干扰重构算法[2]作自干扰抵消：以发送端数字基带信号作抵消参考信号，以失真补偿后的信道训练符号做自干扰信道估计，生成抵消信号，与失真补偿后的信号作差：

可见，非线性自干扰抵消通过降低被抵消信号的残留失真噪声，减小自干扰信道的估计误差，提高了数字抵消的准确性。

基于辅助符号的非线性失真算法步骤见表1。

表1算法步骤

基于辅助符号的非线性失真系数估计算法 开始：接收链路接收到完整数据帧，取出前导码，其余部分送入缓存 1失真映射与提取：(a)估计自干扰信道值；(b)用末端链路取样法[18]获得辅助符号的抵消参考信号；(c)对辅助符号做自干扰抵消，得到结果。 2 失真估计：按照式(5)估计失真系数； 3 失真还原与补偿：根据非线性失真级数和模型，还原失真信号，从原始接收信号中去除失真噪声； 4 自干扰抵消：对失真补偿后的自干扰信号做抵消。

4 算法简化实现方案

一般来说，室内无线局域网(Wireless Local Area Network, WLAN)环境下信道是缓变的，其相关时长不低于ms量级，对于一个物理帧，信道估计的有效时长可持续上百个OFDM符号。失真因子作为硬件参数，可近似认为恒定，因此在实际中，辅助符号的添加可以人为灵活地控制，只需每间隔若干帧对失真因子进行一次估计即可，从而大大降低算法所带来的开销。

但是，算法仍然涉及到现行帧格式的修改，实际系统不便实现。考虑3.1.1节中辅助符号的设计要求，当且仅当提供信道估计结果(用于失真映射)的符号，与接收自干扰抵消的辅助符号并不相同时，才能满足式(3)失真提取、估计的条件，即在抵消残余中，既包括信道估计符号的失真，也包括辅助符号本身的失真。根据这一点，本文在上述算法基础上提出一种简化实现方案：令前导码中两个信道估计符号互为辅助符号，分别对另一符号进行失真映射。为了提高准确性，再将得到的两个估计结果求平均。由此可见，简化方案无需再设置额外的辅助符号，不会增加通信开销。方案示意图如图4所示。

图 4 算法实现简化方案原理框图

5 仿真分析

本节对所提算法性能进行MATLAB仿真实验，为贴近实际，关键参数，如非线性失真强度选自NI571收发机的数据手册[20]；物理帧格式不代表任何一种协议规定，仅为方便数值分析，参数设置见表2。

表2仿真参数设置

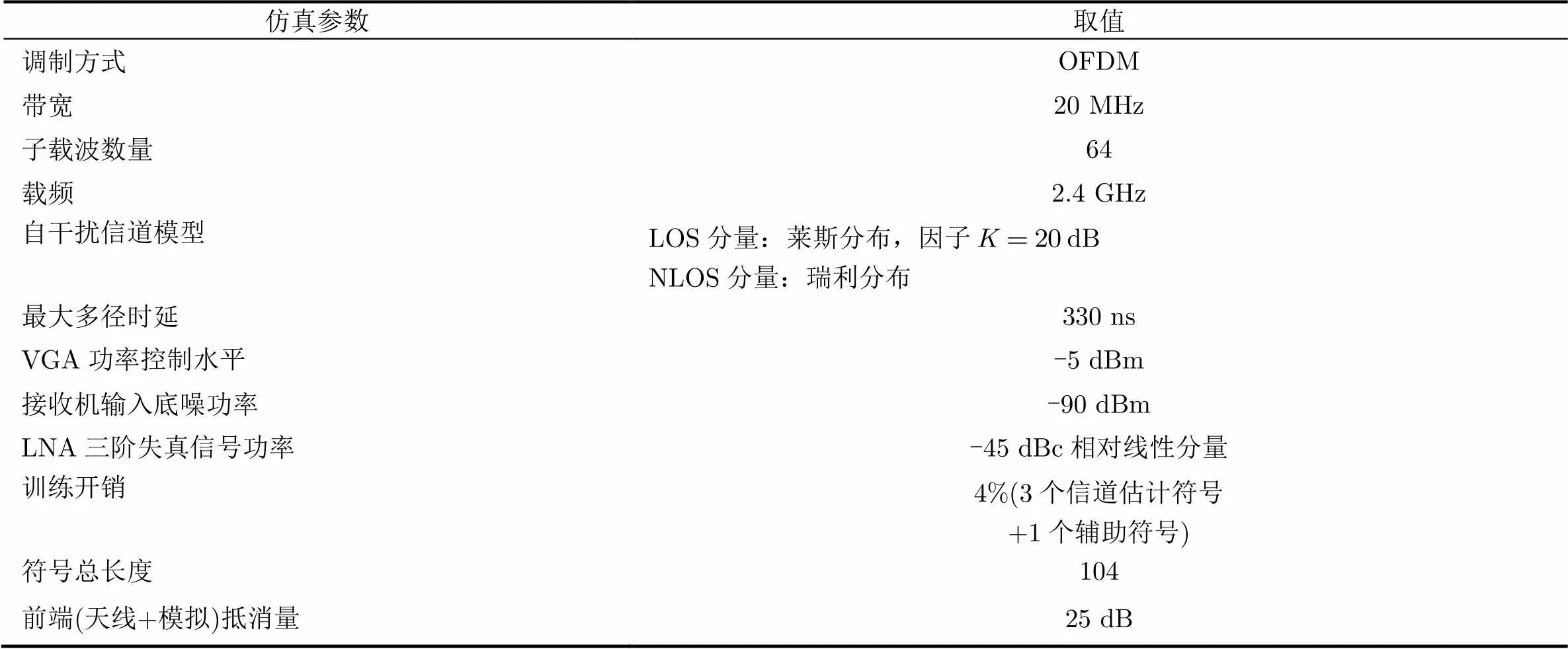
仿真参数取值 调制方式OFDM 带宽20 MHz 子载波数量64 载频2.4 GHz 自干扰信道模型LOS分量：莱斯分布，因子dBNLOS分量：瑞利分布 最大多径时延330 ns VGA功率控制水平-5 dBm 接收机输入底噪功率-90 dBm LNA三阶失真信号功率-45 dBc相对线性分量 训练开销4%(3个信道估计符号+1个辅助符号) 符号总长度104 前端(天线+模拟)抵消量25 dB

非线性抵消算法的两大关键环节是失真估计和失真补偿。下面以自干扰抵消残余强度为指标，分别考察这两个环节中不同的处理方式对算法性能的影响。

5.1失真映射准确性与算法性能

在失真系数估计环节考察失真映射的准确性对算法性能的影响，这一指标反映了对辅助符号做自干扰抵消的结果能否切实地体现信道估计符号的失真。按照映射符号个数不同，本文设置“多信道符号映射”与“单信道符号映射”两组对比方案，其中“多信道符号映射”组又按照映射方式不同分为方案1和方案2。在对信道估计符号有所补偿的前提下，考察不同映射方式对失真估计准确性的影响。见表3。

表3失真映射方式

方案名称方案描述 方案1方案2 多信道符号映射分别对3个信道估计符号做失真映射，得到3个失真系数估计求其平均对3个符号信道估计的平均值做失真映射，得到失真系数估计 单信道符号映射仅对3个信道符号之一做失真映射，得到失真系数估计

从图5(a)，图5(b)可看出，对于多信道符号映射，在对信道估计符号有所补偿的情况下，理想信道值的结果都优于实际估计值。方案1中，理想信道值的增益更为显著，而在方案2中两者差别不大，且性能都不如方案1的两组对应值。

同样在实际信道估计值下，在发送功率-5~20 dBm的变化区间内，方案1的抵消结果变化范围从-150~-100 dBm，比方案2的对应抵消量分别提高了45 dB到20 dB左右，且发送功率越低，其性能提高越显著，这说明方案1的失真映射准确性要高于方案2。原因是，3个信道估计符号各自的非线性失真是互相独立的，分别做失真映射、提取和估计可以得到3个非常接近、只存在微小误差(误差来自于式(1)中高次项，结果证明这一误差并不影响失真系数估计)的失真系数估计，因此再求其平均可以降低误差；而方案2对信道估计取平均的操作使得映射结果已不能有效反映信道估计符号真实的非线性失真，因此失真系数估计结果误差较大。

从图5(c)的结果可以看出，单信道估计符号做失真映射，算法性能相当于多信道符号映射方案1中求平均的3个失真系数估计结果之一，性能略优于方案2，但明显不如方案1。可以推测，若按照方案1的方式估计失真系数，增加信道估计符号数有助于进一步提高算法性能，但也会增大开销。

5.2 失真补偿范围与算法性能

在失真补偿环节，考察补偿范围，研究对信道估计符号补偿与否对算法性能的影响。

从图6(a)可以看出，同样用实际自干扰信道估计做失真系数估计、还原，无论是方案1还是方案2，对信道估计符号做补偿的效果都明显优于无失真补偿；否则，原始信道估计的质量对算法性能的影响区别不大，且均不理想，如图6(b)所示。该实验说明，对无失真的信号做自干扰抵消，自干扰信道估计的准确性是算法性能的决定因素，进一步说明自干扰信道建模是数字抵消算法的重要研究方向。

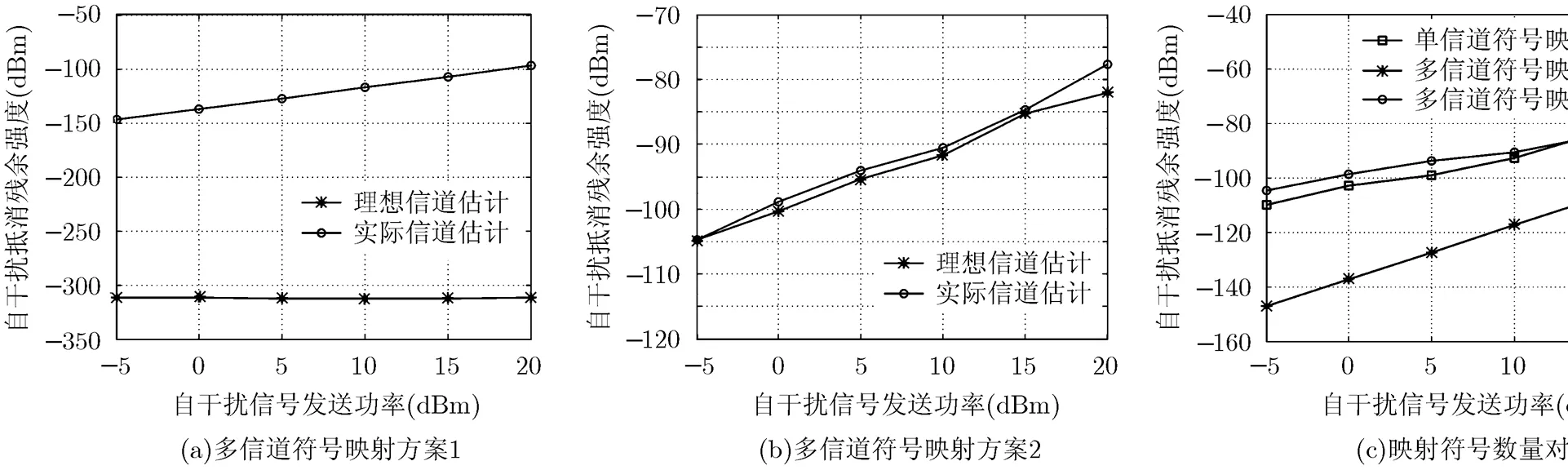
图5 失真映射准确性对算法性能影响(自干扰抵消时信道估计符号有失真补偿)

5.3 简化方案性能

如图7所示，与文献[16]所提出的联合估计算法相比较，在4次迭代(该次数取自文献[16])后，联合估计算法能够达到与本文算法的简化实现方案接近的性能，但仍然不如本文算法。时间复杂度方面，两者均为，但前者的收敛速度与失真系数初值设定密切相关，取值不当易导致算法性能不稳定；其次，文献[16]要求整帧数据反复输入参与运算，这增加了存储空间的消耗和处理时延，而本文算法无需迭代，最少只需要两个符号参与运算。与添加额外辅助符号，并采用多信道符号映射方案1相比，采用实现简化方案避免了额外的通信开销，但代价是抵消性能有所下降。从方案过程描述可以看出，它相当于对不同辅助符号做单信道符号映射的平均结果，对比图5(c)也说明，简化方案性能与单符号映射的结果相当。

图6 失真补偿范围研究 图7 算法实现简化方案性能

6 结束语

全双工的推广应用受限于自干扰非线性失真对抵消算法性能的影响，针对现有非线性抵消算法中存在的信道估计和失真系数估计互相耦合的问题，本文设计了基于辅助符号的非线性抵消算法，在根据自干扰抵消结果估计失真系数时，将信道估计符号的非线性失真考虑进来，通过对辅助符号做自干扰抵消，将信道估计符号的非线性失真映射到抵消结果中，作为失真载体之一提取出来。仿真结果表明，算法能有效提高自干扰抵消算法性能，采用实现简化方案则可避免辅助符号引入额外通信开销。

[1] CHOI J I, JAIN M, SRINIVASAN K,. Achieving single channel, full duplex wireless communications[C]. Proceedings

of the 16th Annual International Conference on Mobile Computing and Networking, Chicago, IL, USA, 2010: 1-12. doi: 10.1145/1859995.1859997.

[2] JAIN M, CHOI J I, KIM T,. Practical, real-time, full duplex wireless[C]. Proceedings of 17th Annual International Conference on Mobile Computing and Networking, Las Vegas, NV, USA, 2011: 301-312. doi: 10.1145/2030613.2030647.

[3] DUARTE M and SABHARWAL A. Full-duplex wireless communications using off-the-shelf radios: Feasibility and first results[C]. Proceedings of the 44th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2010: 1558-1562. doi: 10.1109/ACSSC.2010.5757799.

[4] SAHAI A, PATEL G, and SABHARWAL A. Pushing the limits of full-duplex: Design and real-time implementation[R]. Houston: Rice University, 2011.

[5] SABHARWAL A, SCHNITER P, Guo Dongning,. In-band full-duplex wireless: challenges and opportunities[J]., 2014, 32(9): 1637-1652. doi: 10.1109/JSAC.2014.2330193.

[6] SAMPATH R, MOHAMMAD A, KARTHIK S,. The case for antenna cancellation for scalable full-duplex wireless communications[C]. Proceedings of the 10th ACM Workshop on Hot Topics in Networks, Toronto, Canada, 2011: 1-6. doi: 10.1145/2070562.2070579.

[7] EVAN E, MELISSA D, CHRIS D,. Empowering full- duplex wireless communication by exploiting directional diversity[C]. Proceedings of Asilomar Conference of the 45th Signals, Systems and Computers, Pacific Grove, CA, USA, 2011: 2002-2006. doi: 10.1109/ACSSC.2011.6190376.

[8] WANG Jun, ZHAO Hongzhi, and TANG Youxi. A RF adaptive least mean square algorithm for self-interference cancellation in co-frequency co-time full duplex systems[C]. Proceedings of Conference of IEEE International Conference on Communications, Sydney, Australia, 2014: 5622-5627. doi: 10.1109/ICC.2014.6884217.

[9] EVAN E, ACHALESHWAR S, and ASHUTOSH S. Passive self-interference suppression for full-duplex infrastructure nodes[J]., 2014, 13(2): 680-694. doi: 10.1109/TWC.2013.010214. 130226.

[10] DUARTE M, DICK C, and SABHARWAL A. Experiment- driven characterization of full-duplex wireless systems[J]., 2012, 11(12): 4296-4307. doi: 10.1109/TWC.2012.102612.111278.

[11] KORPI D, RIIHONEN T, SYRJALA V,. Full-duplex transceiver system calculations: analysis of ADC and linearity challenges[J]., 2014, 13(7): 3821-3836. doi: 10.1109/ TWC.2014.2315213.

[12] BHARADIA D, MCMILIN E, and KATTI S. Full duplex radios[C]. Proceedings of Conference of the ACM Special Interest Group on Data Communication, Hong Kong, China, 2013: 375-386. doi: 10.1145/2486001.2486033.

[13] OMER M, RIMINI R, HEIDMANN P,. A compensation scheme to allow full duplex operation in the presence of highly nonlinear microwave components for 4G systems[C]. Proceedings of Conference of IEEE MTT-S International Microwave Symposium Digest, Baltimore, MD, USA, 2011: 1-4. doi: 10.1109/MWSYM.2011.5973395.

[14] ANTTILA L, KORPI D, SYRJALA V,. Cancellation of power amplifier induced nonlinear self-interference in full- duplex transceivers: Signals, systems and computers[C]. Proceedings of Conference of 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2013: 1193-1198. doi: 10.1109/ACSSC.2013.6810482.

[15] KORPI D, ANTTILA L, and VALKAMA M. Feasibility of in-band full-duplex radio transceivers with imperfect RF components: analysis and enhanced cancellation algorithms [C]. Proceedings of 9th International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Oulu, Finland, 2014: 532-538.

[16] AHMED E, ELTAWIL A M, and SABHARWAL A. Self- interference cancellation with nonlinear distortion suppression for full-duplex systems: signals, systems and computers[C]. Proceedings of the IEEE Conference of 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2013: 1199-1203. doi: 10.1109/ ACSSC.2013.6810483.

[17] SCHENK T. RF Imperfections in High-rate Wireless Systems, Impact and Digital Compensation[M]. New York: Springer Netherlands, 2008: 185-243.

[18] ELSAYED A and AHMED M E. All-digital self-interference cancellation technique for full-duplex systems[J]., 2015, 14(7): 3519-3532. doi: 10.1109/TWC.2015.2407876.

[19] 史治国, 洪少华, 陈抗生. 基于Xilinx FPGA的OFDM通信系统基带设计[M]. 杭州: 浙江大学出版社, 2009: 37-38.

SHI Zhiguo, HONG Shaohua, and CHEN Kangsheng. Xilinx FPGA-Based Baseband OFDM Communication System Design[M]. Hangzhou: Zhejiang University Press, 2009: 37-38.

[20] National Instrument. NI 5791r User Manual and Specifi- cations[OL]. http://www.ni.com/pdf.manuals/ 373845d.pdf, 2015.

王 丹： 女，1991年生，博士生，研究方向为无线移动通信.

黄开枝： 女，1973年生，教授，博士后，主要研究方向为无线移动通信及其安全.

李云洲： 男，1974年生，副研究员，主要研究方向为无线移动通信.

Auxiliary Symbol-based Nonlinear Self-interference Cancellation Algorithm and Simplified Implementation

WANG Dan①②HUANG Kaizhi①LI Yunzhou②

①(&&,,450002,)②(&,,100084,)

In-bandfull duplex is a key concept brought up in 5G, and digital Self-Interference (SI) cancellation has become an important field attracting much attention. SI channel estimation error introduced by nonlinear distortion leads to deleterious effect on the accurate estimation of distortion coefficient. This paper proposes a nonlinear SI cancellation algorithm based on an auxiliary symbol. The channel estimation error is mapped into cancellation residuals by performing SI cancellation for the designed auxiliary symbol, and then extracted to be an independent attributor for distortion coefficient estimation. A simplified implementation is proposed further for reducing the overhead of the algorithm. Simulation results show that the nonlinear SI component is suppressed to about -100 dBm with -5 dBm SI power received. In addition, the lower the received SI power is, the better the performance tends to be.

5G; In-band full duplex; Digital Self-Interference (SI) cancellation; Nonlinear distortion estimation

TN929.53

A

1009-5896(2017)01-0024-07

10.11999/JEIT160291

2016-03-28；改回日期：2016-09-06；

2016-11-14

王丹 wangdan910503@mail.tsinghua.edu.cn

国家973计划项目(2013CB329002)，国家863计划项目(2014AA01A703)，国家重大专项(2014ZX03003002-002)，新世纪优秀人才支持计划(NCET-13-0321)，国家自然科学基金创新群体(61321061)

The National 973 Program of China (2013CB 329002), The National 863 Program of China (2014AA01A703), The National Major Project (2014ZX03003002-002), The Program for New Century Excellent Talents in University (NCET-13-0321), The National Natural Science Foundation of Innovation Group (61321061)