例析立体几何中的“体积恒等法”

☉江苏省苏州市吴县中学 戴兰娟

例析立体几何中的“体积恒等法”

☉江苏省苏州市吴县中学 戴兰娟

“体积恒等法”就是借助几何体本身在结构上固有的特点，变换视角，将一个几何体的体积等价转化成另一个便于求出体积的几何体，从而解决问题.立体几何中，一般用“体积恒等法”来计算几何体的体积、点到平面的距离、直线与平面所成角等问题，解题过程中，转化与化归的思想无处不在.本文借助实例来谈谈“体积恒等法”在立体几何中的具体应用.

一、求体积

例1 如图1，在正三棱柱ABC-A1B1C1中，已知AB=AA1=3，点P在棱CC1上，则三棱锥P-ABA1的体积为______.

解析：考虑到棱柱中CC1∥平面ABA1，所以P到平面ABA1的距离与C到平面ABA1的距离相等，这样就把三棱锥P-ABA1的体积转化成三棱锥C-ABA1的体积.

图1

图2

例2 如图2，在正四棱柱ABCD-A1B1C1D1中，AB=3cm，AA1=1cm，则三棱锥D1-A1BD的体积为________cm3.

解析：直接求D1到平面A1BD的距离有相当大的难度.因为垂足不易找，所以可以换个角度求三棱锥B-A1DD1的体积.而B到面A1DD1的距离为BA=3，

点评：这是两个求几何体体积的基础题目，考查了学生对锥体体积公式的运用，特别是对三棱锥这个特殊的四面体的认识程度.对于三棱锥的体积问题，通常都需要变换顶点与底面的相对位置，以便于找到三棱锥的高，往往涉及转化思想的运用.

二、求点到平面的距离

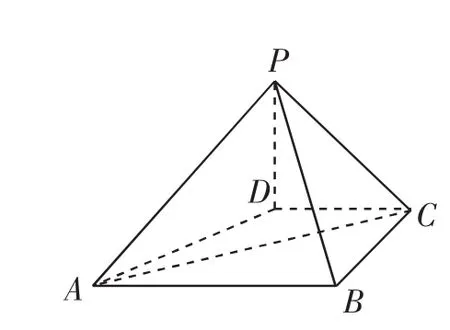
图3

例3 如图3，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°.

（1）求证：PC⊥BC；

（2）求点A到平面PBC的距离.

解析：（1）证明略.

（2）要求点A到平面PBC的距离，其实就是求三棱锥A-PBC的一条高，可以利用体积恒等法求解.设点A到平面PBC的距离为h，由VA-PBC=VP-ABC可知PD，即

图4

例4 如图4，在圆锥VO中，O为底面圆的圆心，点A，B在圆O上，且OA⊥OB，若OA=VO=1，则点O到平面VAB的距离为__________.

解析：本题是典型的运用体积恒等法求距离的题目.设点O到平面VAB的距离为h，由VV-AOB=VO-ABV可知，，即

点评：在立体几何中，求点到平面的距离问题，常常可以转化到三棱锥中，其实就是求某个特定的三棱锥的高的问题.再利用三棱锥的特殊的结构特点，运用体积恒等法，问题就迎刃而解了.

三、求线面所成角

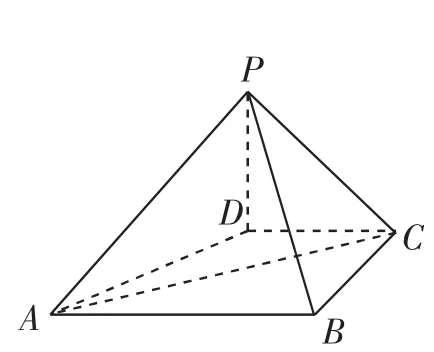
图5

例5 如图5，在四棱锥PABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°.求直线AB与平面PBC所成角的大小.

点评：在立体几何中，求直线与平面所成角问题时，关键要找准垂足（或求出点到面的距离），这样线面所成角的问题就转化成线线所成角的问题.

通过以上实例，不难发现，利用“体积恒等法”可以回避寻找垂足的具体位置，降低了思维难度，省去了许多烦琐的作图与论证过程.在解题过程中，遇到上述问题，若能恰当地运用“体积恒等法”，便能在很大程度上提高解题效率，达到事半功倍的效果.