一种改进的高精度频率源钟差仿真方法

徐 超，李 博，刘军良，吴华兵，胡永辉

(1.中国科学院国家授时中心，西安 710600；2.中国科学院时间频率基准重点实验室，西安 710600；3.中国科学院大学，北京 100190)

一种改进的高精度频率源钟差仿真方法

徐 超1,2,3，李 博1,2,3，刘军良1,2，吴华兵1,2，胡永辉1,2

(1.中国科学院国家授时中心，西安 710600；2.中国科学院时间频率基准重点实验室，西安 710600；3.中国科学院大学，北京 100190)

提出了一种适用于高精度频率源仿真的钟差仿真方法。从频率源的噪声特性及噪声幂率谱模型入手，利用[-1,1]范围内服从均匀分布的随机变量模拟各类噪声的特性，并给出了各类噪声模拟产生的数学表达式。在此基础上，提出了基于牛顿迭代法求解噪声参数的新方法，避免了噪声参数拟合过程中进行线性近似带来的误差，并进行了试验验证。试验结果表明，所提出的钟差模拟方法适用于不同类型的原子钟以及高稳晶振的钟差模拟仿真，模拟产生的钟差数据的阿伦偏差与实测值非常接近，能很好地反映各种噪声对钟差数据的影响，可以满足高精度频率源模拟仿真的需求。

原子钟；高稳晶振；钟差；幂率谱噪声；牛顿迭代

0 引 言

高精度频率源在时频实验室、导航、通信、深空探测等许多领域中应用越来越广泛[1-3]，其钟差仿真能够为系统设计方案的评估、算法的仿真和应用的开发等提供可靠的验证手段，因此也越来越受到系统设计者的重视。

对振荡器噪声的建模及仿真是钟差仿真的基础，文献[4]对闪烁噪声的特性进行了深入的研究，提出了使用白噪声模拟产生闪烁噪声的方法；文献[5-7]分别对几种常用的噪声仿真模型进行了讨论，并给出了仿真结果；文献[8]提出了一种仿真幂律谱噪声的新方法，其基本思路是将幂律谱噪声x(t)看成是白噪声w(t)通过一个线性系统的输出，并给出了在连续域和离散域求解系统冲击响应h(t)的方法；文献[9]提出了一种利用服从均匀分布的随机变量模拟幂律谱噪声的简便方法，并给出了时域表达式，文献[10]对该方法进行了改进，加入了归一化系数，使产生的各种噪声的阿伦方差保持不变，并给出了使用线性最小二乘法求解噪声参数的方法。

噪声参数的选取对于最后仿真结果有着较大影响，不准确的噪声参数会使得模拟产生的钟差数据的阿伦方差与实测的阿伦方差产生较大偏离。本文提出了一种基于牛顿迭代法计算噪声系数的方法，能准确的模拟频率源的噪声特性，与文献[10]的方法相比，该方法模拟产生的钟差数据的阿伦方差与实测值具有更好的符合度。

1 钟差仿真建模

1.1钟差信号的表示

钟差指的是由频率源瞬时相位变化引起的相对于参考系理想时间的相对时间偏差[11]。对于一个频率源，瞬时频率相对于标称频率的偏差y(t)定义为

(1)

式中：v0为标称频率，v(t)为输出信号的瞬时频率，y(t)表示输出信号的瞬时频率相对于标称频率的归一化瞬时频率偏差。相对频率偏差y(t)在时域上的积分定义为钟差x(t)：

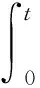
(2)

(3)

1.2频率源噪声模型

对于一个频率源而言，钟差信号的不稳定主要源于频率源的物理特性和外部环境所引起的各种随机噪声。幂率谱噪声模型是使用最广泛的频率源噪声模型，它的有效性已经被许多实验结果所证实，并为国际学术界所普遍接受[11]。

幂率谱噪声模型是用5种相互独立的随机噪声来描述振荡器的频率波动过程，并通过输出频率的功率谱密度函数在对数域的斜率来区分各种不同的噪声类型，功率谱密度函数表示为[12-13]

(4)

式中：hα为常数，α=-2,-1,0,1,2分别对应随机游走噪声、频率闪烁噪声、频率白噪声、相位闪烁噪声、相位白噪声5种不同的噪声类型。

对于高精度频率源钟差模拟仿真而言，往往更关注这些噪声在时间x(t)上的表现。由于时间是频率的积分，x(t)的功率谱密度函数表示为：

(5)

将式(4)代入式(5)，可得

(6)

式中:功率谱密度函数Sx(f)在对数域的表示如图1所示。

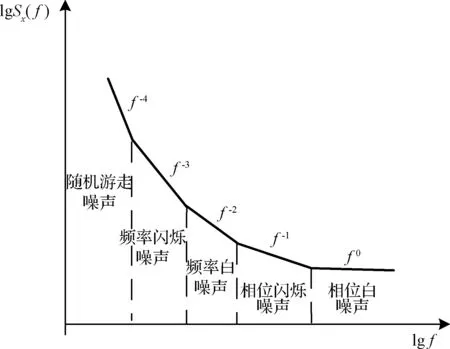
图1 不同噪声的功率谱密度Fig.1 Power spectral density of typical clock noise

如图1所示，不同的曲线斜率可以区分不同类型的随机噪声。随机游走噪声是最低频的噪声，其对长期频率稳定度的影响较大，而从短期来看，相位白噪声则对频率稳定度的影响最大。

阿伦方差是常用的频率稳定度的时域表征，定义为[13]

(7)

式中：τ表示采样时间，N表示以τ为采样间隔的样本数。在实际应用中，一般采用阿伦方差的平方根来表征，即阿伦偏差。

阿伦方差与谱密度Sy(f)之间存在转换关系，其表达式为

(8)

在实际测量过程中，系统输出一般需要经过一个低通滤波器，进入低通滤波器的频率超过滤波器的截止频率fh时便被抑制，此时表达式为

(9)

其中,低通滤波器的截止频率fh满足：

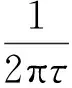
(10)

结合式(4)和式(9)可以得到幂率谱噪声的阿伦方差，结果如表1所示，对于钟差信号的仿真也是基于表1内容展开的。

表1 各种噪声功率谱密度与阿伦方差换算表Table 1 Conversion table of noise power spectral density and Allan variance

1.3频率源噪声模拟方法

一般情况，在进行钟差数据模拟产生时，可以忽略相位闪烁噪声[9-10]。本小节主要对其他四种噪声进行分析。

令

作为四种噪声的噪声参数，将上述噪声参数代入表1，各种噪声与阿伦方差之间的函数关系如表2所示。

使用服从均匀分布的随机变量能很好的模拟各种噪声的特性，各种噪声引起的相对频率偏差的表达式为[9]

表2 各种噪声与阿伦方差Table 2 Allan variance of types of clock noise

(11)

(12)

(13)

式中：D(i)为[-1,1]范围内的服从均匀分布的随机变量，i=1,2,…,N，N为仿真数据点数，τs为采样周期。

使用式(11)～(13)可以很容易的模拟产生相位白噪声、频率白噪声和随机游走噪声的相对频率偏差。然而，频率闪烁噪声的模拟产生则比较不容易，文献[14]中提出了模拟产生频率闪烁噪声的方法，取得了很好的效果。其表达式为

(14)

在使用上述方法产生各种噪声引起的相对频率偏差数据时，必须加入一个归一化常量k，如表3[10]所示，以使得产生的各种噪声数据的阿伦方差保持不变。

表3 归一化系数Table 3 Normalized coefficient

按照上述方法，能够模拟产生各类噪声的相对频率偏差，再将式(11)～(14)代入式(2)，便可得到钟差的模拟数据，钟差数据产生的表达式为：

x(i)=x(i-1)+[ywp(i)+

ywf(i)+yff(i)+yrw(i)]τs

(15)

2 基于牛顿迭代法的噪声参数拟合方法

文献[10]提出了一种确定噪声参数的方法。利用对频率源的实际测量得到的钟差数据，计算出多个阿伦偏差，再利用线性最小二乘方法及非负的约束条件，可以计算得到噪声参数，其表达式为：

(16)

式中：fh=1 Hz，σy为阿伦偏差。

采用上述方法进行噪声参数确定时，式(16)的各个等式是对阿伦偏差表达式(17)的线性近似，其阿伦偏差与理论值存在一定的偏差，如图2所示，这一偏差将对噪声参数的拟合造成较大的影响。

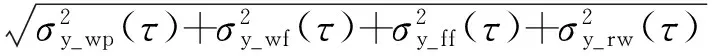
(17)

图2 某典型氢原子钟的阿伦偏差Fig.2 Allan standard deviation of a typical hydrogen atomic clock

在实际应用过程中，需要使得模拟产生的钟差数据符合某特定频率源的统计特性。因此，将该频率源的阿伦偏差作为输入，将式(16)按照式(17) 进行修正，得到如下超定非线性方程组。

(18)

牛顿迭代法是求解非线性方程组的常用有效方法之一，可以用于求解上述超定非线性方程组的最优解A=[Awp,Awf,Aff,Arw][15]。

(19)

超定非线性方程组的一般形式如式(19)所示，其中,fi(x1,x2,…,xn)是定义在区域D⊂Rn上的实值函数，m>n。按照牛顿迭代法求得方程组迭代k+1次后的解Xk+1为

(20)

(21)

在式(20)中，G(Xk)被加上了下标，是因为每一次更新Xk+1以后，F(X)的Jacobi矩阵都要重新计算。更新结束的条件是通过判断X是否收敛，即当修正量ΔXk满足

ΔXk<ΔXth

(22)

其中,ΔXth是预先设定的一个阈值，当ΔXk小于该阈值时，就认为可以停止更新了。X的收敛只是意味着我们已经找到了使最小二乘的代价函数最小的解，并不是说代价函数已经趋于0。

在使用牛顿迭代法解非线性方程组时，如果迭代矩阵G(Xk)出现奇异或病态情况，迭代式(20)往往无法进行或者很难奏效。因此，为了解决迭代过程中G(Xk)出现奇异或病态的问题，可以采用阻尼牛顿法对牛顿迭代法进行修正[15]。

阻尼牛顿法是在牛顿迭代法的基础上增加一个阻尼因子α∈(0,1]，使得

Xk+1=Xk+αp

(23)

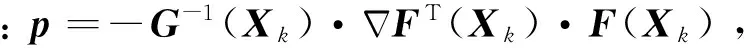
(24)

图3 阻尼牛顿法求解非线性方程组流程图Fig.3 The flow chart of solve nonliner equation using damped Newton iteration

3 试验结果

3.1氢原子钟试验结果

试验利用国家授时中心守时实验室的两台氢原子钟MHM2010，采用互比法[18]测量其频率稳定度。利用本文中的方法模拟产生钟差数据，计算其阿伦偏差，以MHM2010的实测阿伦偏差数据为参考，比较两种钟差仿真方法产生的钟差数据的阿伦偏差与参考值的偏差，试验结果见图4和表4。

从图4和表4可以看出，与文献[10]的采用最小二乘法确定噪声参数的钟差仿真方法相比，采用本文提出的基于牛顿迭代法的钟差仿真方法模拟产生的钟差数据的阿伦偏差与实测值之间的偏差更小，能更好地反映各种噪声对钟差数据的影响。

图4 某台氢钟MHM2010模拟钟差数据阿伦偏差与实测值Fig.4 Allan deviation of a MHM2010 hydrogen atomic clock

τ/s实测值最小二乘法牛顿迭代法12×10-131.64×10-132.00×10-13103×10-142.03×10-142.94×10-141006×10-154.44×10-157.65×10-1510003×10-151.81×10-153.00×10-15100002.5×10-151.38×10-152.17×10-15864002×10-151.50×10-152.65×10-15

3.2铯原子钟试验结果

试验采用以国家授时中心守时实验室的主钟信号为参考，利用高性能相噪与阿伦偏差分析仪5120A测得的某台HP5071A铯原子钟的频率稳定度实测数据。按照本文中的钟差仿真方法模拟产生钟差数据，计算其阿伦偏差，以HP5071A的实测阿伦偏差数据为参考，比较两种钟差仿真方法产生的钟差数据的阿伦偏差与参考值的偏差，试验结果见图5和表5。

图5 某台铯钟HP5071A模拟钟差数据阿伦偏差与实测值Fig.5 Allan deviation of a HP5071A cesium atomic clock

τ/s实测值最小二乘法牛顿迭代法103.00×10-122.53×10-123.01×10-12202.03×10-121.77×10-122.03×10-12401.38×10-121.25×10-121.39×10-121008.7×10-137.88×10-138.67×10-132005.99×10-135.59×10-136.10×10-134004.06×10-133.94×10-134.31×10-1310002.7×10-132.51×10-132.73×10-1320001.93×10-131.80×10-131.94×10-1340001.12×10-131.32×10-131.39×10-13100005.2×10-141.0×10-139.06×10-14

与图4氢原子钟的试验结果相比，两种方法仿真产生的钟差数据的阿伦偏差与实测值的偏差相差不大，本文提出的钟差仿真方法的拟合精度只略优于文献[10]的采用最小二乘法确定噪声参数的钟差仿真方法。这是由于τ≤10000 s区间内，铯原子钟主要受频率白噪声的影响[19]，此时其他类型的噪声对频率稳定度的影响较小，所以式(16)在对式(17)线性近似时引入的误差较小。

3.3铷原子钟试验结果

与第3.2节铯原子钟试验方法类似，以同样方法测得的某台PRS10铷原子钟的频率稳定度实测数据为参考，按照两种钟差仿真方法分别产生钟差数据，计算并比较其阿伦偏差与参考值的偏差，结果见图6和表6。

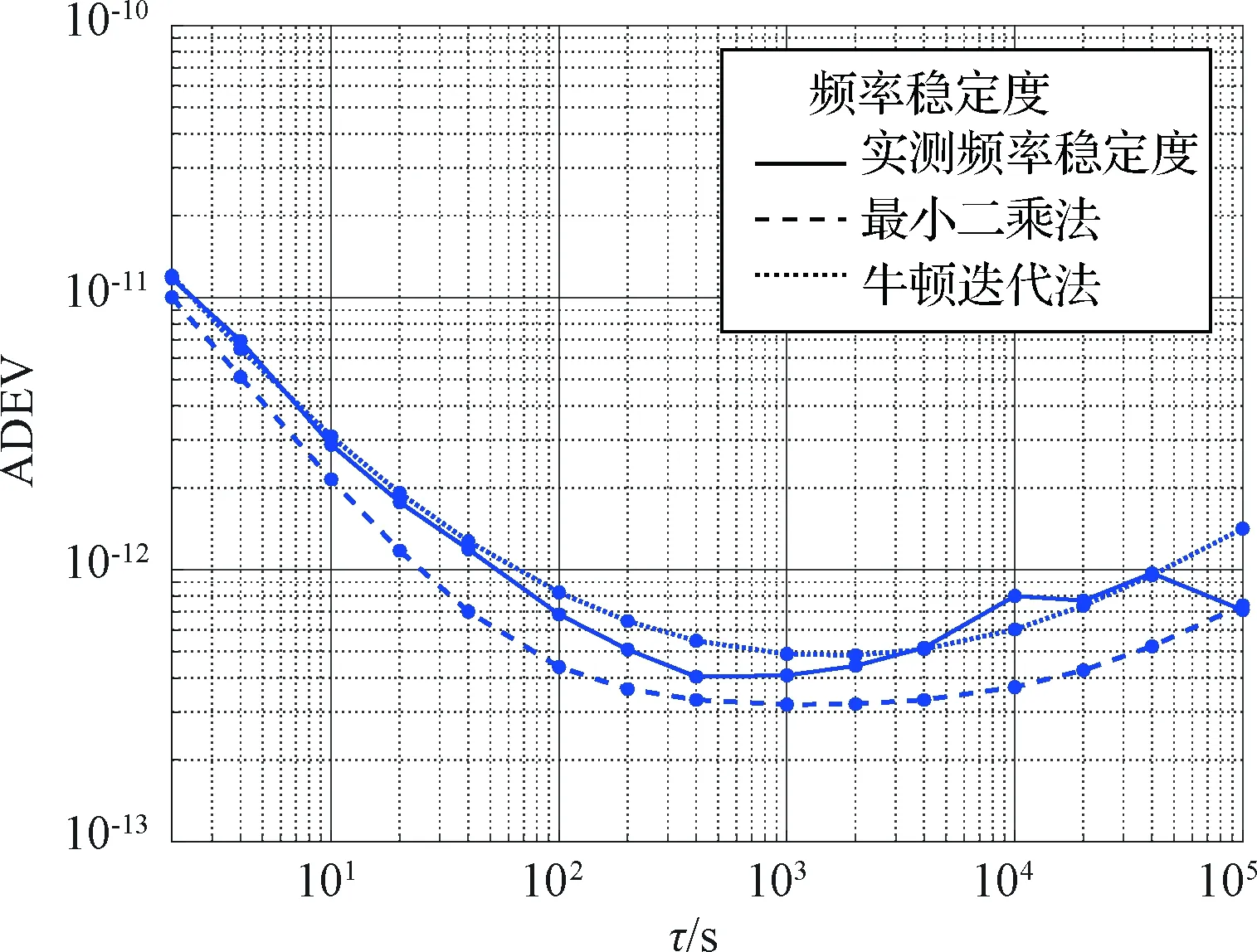
图6 某台铷钟PRS10模拟钟差数据阿伦偏差与实测值Fig.6 Allan deviation of a PRS10 rubidium atomic clock

图6和表6的试验结果表明，铷原子钟的试验结果与氢原子钟的试验结果类似。本文提出的钟差仿真方法较之文献[10]提出的采用最小二乘法确定噪声参数的钟差仿真方法有较为明显的改善，模拟产生的钟差数据的阿伦偏差与实测值更接近，能更好地体现各种噪声对钟差数据的影响。

表6 某台铷钟PRS10模拟钟差数据阿伦偏差与实测值Table 6 Allan deviation of a PRS10 rubidium atomic clock

3.4高稳晶振试验结果

高稳晶振OSA8607的频率稳定度数据来源与第3.2节、第3.3节相同，均为实际测量数据。采用与前文同样的试验方法，比较两种方法产生的钟差数据的阿伦偏差与实测值的偏差，结果见图7和表7。

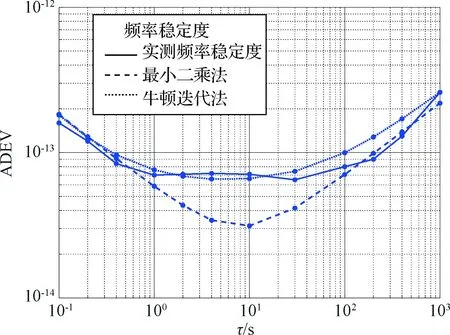
图7 某高稳晶振OSA8607模拟钟差数据阿伦偏差与实测值Fig.7 Allan deviation of a OSA8607 high stability OCXO

τ/s实测值最小二乘法牛顿迭代法0.11.6×10-131.83×10-131.87×10-1317×10-145.87×10-147.6×10-14107.1×10-143.14×10-146.62×10-141008×10-147.07×10-149.98×10-1410002.6×10-132.19×10-132.60×10-13

采用最小二乘法模拟产生的钟差数据的阿伦偏差与实测的频率源的阿伦偏差在τ=1～100 s区间存在较大偏差，已经不能反映高稳晶振实际的频率稳定度特性，而本文提出的原子钟钟差模拟方法模拟产生的钟差数据的阿伦偏差与实测值偏差较小，在统计学意义上能很好的反映各种噪声对钟差数据的影响。

综上所述，与文献[10]提出的采用最小二乘法确定噪声参数的钟差模拟方法相比，本文所提出的钟差仿真方法在对噪声参数的拟合建模过程中，避免了由于对式(17)进行线性近似而带来的误差，更加符合其频率稳定度的统计特性。模拟产生的钟差数据的阿伦偏差与实测值的更加接近，能更好的反映各种噪声对钟差数据的影响，适用于不同类型的原子钟和高稳晶振的钟差模拟仿真。

4 结 论

本文从频率源的噪声特性及噪声幂率谱模型入手，提出了一种准确且简便的模拟高精度频率源钟差信号的方法，模拟产生钟差数据的阿伦偏差与给定的频率源的阿伦偏差几乎一致。该方法允许在不失实际随机行为的情况下，对高精度频率源的噪声行为进行深度的分析，能够方便的应用于时频实验室、卫星导航系统、高精度通信系统、深空探测等许多领域的算法验证和应用开发。

[1] 唐升,刘娅,李孝辉. 星载原子钟自主完好性监测方法研究[J]. 宇航学报, 2013, 34(1):39-45.[Tang Sheng,Liu Ya,Li Xiao-hui. A study on onboard satellite atomic clock autonomous integrity monitoring[J]. Journal of Astronautics, 2013, 34(1):39-45.]

[2] 张小红,陈兴汉,郭斐. 高性能原子钟钟差建模及其在精密单点定位中的应用[J]. 测绘学报, 2015, 44(4):392-398. [Zhang Xiao-hong, Chen Xing-han, Guo Fei. High performance atomic clock modeling and its application in precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4):392-398.]

[3] Schäfer W, Devicente J. ESA′s frequency and timing systems for deep space operations and radio science investigations[C]. The 20th European Frequency and Time Forum, Braunschweig, Germany, March 27-30, 2006.

[4] Barnes J A, Jarvis S. Efficient numerical and analog modeling of flicker noise processes[R]. Washington DC: U.S. Government Printing Office, June 1971.

[5] Kartaschoff P. Computer simulation of the conventional clock model[J]. IEEE Transactions on Instrumentation and Measurement, 1979, 28(3): 193-197.

[6] Radeka V. 1/|f| noise in physical measurements[J]. IEEE Transactions on Nuclear Science, 1969, 16(5): 17-35.

[7] Riggs T L, Phillips C L. Modeling continuous noise sources in digital simulations[J]. Simulation, 1987, 48(1): 11-18.

[8] Kasdin N J, Walter T. Discrete simulation of power law noise[C]. The 46th Frequency Control Symposium, Hershey, PA, USA, May 27-29, 1992.

[9] Harting A. Considering clock errors in numerical simulations[J]. IEEE Transactions on Instrumentation and Measurement, 1996, 45(3): 715-720.

[10] Diez J, D′Angelo P, Fernández A. Clock errors simulation and characterisation[C]. ION GNSS 19th International Technical Meeting of Satellite Division,Fort Worth,TX Sep 26-29,2006.

[11] 漆贯荣. 时间科学基础[M]. 北京：高等教育出版社, 2006.

[12] 翟造成, 张为群, 蔡勇, 等. 原子钟基本原理与时频测量技术[M].上海: 上海科学技术文献出版社,2009.

[13] Barnes J A, Chi A R, Cutler L S, et al. Characterization of frequency stability[J]. IEEE Transactions on Instrumentation and Measurement, 1971, 20(2): 105-120.

[14] Barnes J A, Allan D W. A statistical model of flicker noise[J]. Proceedings of the IEEE, 1966, 54(2): 176-178.

[15] 陈淑铭,乔田田. 一个求解非线性最小二乘问题的新方法[J]. 烟台大学学报: 自然科学与工程版, 2004, 17(1): 14-22. [Chen Shu-ming, Qiao Tian-tian. A new method for solving problems of nonlinear least square [J]. Journal of Yantai University: Natural Science and Engineering Edition, 2004, 17(1): 14-22.]

[16] 张建军,李春泉,张烈辉. 影响阻尼牛顿法收敛性的两个重要参数[J]. 纯粹数学与应用数学, 2012, 28(4): 433-439. [Zhang Jian-jun, Li Chun-quan, Zhang Lei-hui. The effect of two important parameter upon the convergence in damped newton method[J]. Pure and Applied Mathematics, 2012,28(4):433-439.]

[17] 朱小飞. 迭代法解非线性方程组[D]. 合肥：合肥工业大学, 2014. [Zhu Xiao-fei. Some iterative methods for solving system of nonlinear equations[D]. Hefei: Hefei University of Technology, 2014.]

[18] JJG 1004—2005, 氢原子频率标准检定规程[S].

[19] 张敏. 原子钟噪声类型和频率稳定度估计的自由度分析与探讨[D]. 北京：中国科学院研究生院, 2008. [Zhang Ming. Analysis of the noise type of atomic clock and the degree of freedom of frequency stability[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2008.]

AModifiedMethodforClockErrorSimulationofHighPrecisionFrequencySource

XU Chao1,2,3, LI Bo1,2,3, LIU Jun-liang1,2, WU Hua-bing1,2, HU Yong-hui1,2

(1.National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2.Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3.University of the Chinese Academy of Sciences, Beijing 100190, China)

An advanced approach to generating clock errors is presented that fits a high precision frequency source. Starting from the noise characteristics and noise power spectrum model, a new method for solving the noise parameters based on the Newton iterative method is proposed. Using these results as input, a sequence of clock errors are then obtained using the random variable subject to the uniform distributionin the range of [-1,1].Then, an experiment is carried out to test the performance of this simulation method. The Allan deviation of the simulation data is close to the reference value, and can reflect the effect of all kinds of noise on clock errors. It refers that the proposed simulation method is applicable for the clock error simulation of different types of atomic clocks and high stability crystal oscillators.

Atomic clock; High stability OCXO; Clock error; Power law noise; Newton iterative

TH714.1+4

A

1000-1328(2017)09- 0998- 08

10.3873/j.issn.1000-1328.2017.09.013

2017- 05- 11;

2017- 07- 17

中国科学院西部青年学者项目(XAB2015B13); 中国科学院西部青年学者资助项目(XAB2015B16)

徐超(1989-)，男，博士生，主要从事高精度时间频率测量控制方法和技术研究。

通信地址：陕西省西安市临潼区书院东路3号中国科学院国家授时中心(710600)

电话：(029)83890244

E-mail:xuchao1226@126.com