低成本高超声速试验火箭姿态控制方法

吴东升，郑忠培，丁智坚

(1.中国空气动力研究与发展中心吸气式高超声速技术研究中心，绵阳 621000；

低成本高超声速试验火箭姿态控制方法

吴东升1，郑忠培2，丁智坚1

(1.中国空气动力研究与发展中心吸气式高超声速技术研究中心，绵阳 621000；

2.中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000)

针对我国低成本高超声速试验火箭的需求，提出一种基于简易反作用控制系统(RCS)的进动和章动同步控制方法，实现高空旋转火箭的大范围姿态调整和再入姿态控制。该方法采用单喷管且喷气冲量固定的RCS执行机构，通过对旋转火箭在RCS间歇作用下动力学演进过程分析，建立了体现进动、章动耦合效应的状态空间模型和系统稳定条件，设计了开关控制策略。利用姿态角和角速率构建反馈信号控制RCS喷管开启，使姿态角满足要求。理论仿真表明：在RCS喷气冲量矩相对误差为26.7%，自旋角速度变化范围为2.0～4.0 r/s的条件下，仍然可以实现大范围俯仰角调整(+10°～-60°)。该方法可以应用于我国低成本高超声速试验火箭，推动高超声速研究性飞行试验广泛开展。

高超声速；自旋火箭；姿态控制；反作用控制系统；进动；章动

0 引 言

为了深化对高超声速基础科学问题认知，国外大力发展低成本高超声速试验火箭技术，典型飞行试验包括HyShot、HIFiRE、SHEFEX等。这种经济、高效的飞行试验，被认为开拓了吸气式发动机飞行试验的新时代，是高超声速飞行试验的先驱[1-4]。这类火箭在大气层内利用斜置安定面稳定进行无控飞行，在大气层外通过自旋实现姿态稳定，利用简易反作用控制系统(Reaction control system，RCS)完成掉头和再入姿态调整，进入试验窗口后开展相关飞行试验[5-8]。尽管简易姿态控制系统已经成为这类火箭的标准配置，但国外相关文献只有仿真和飞行试验结果，没有提及具体控制方法。随着我国高超声速技术研究的深入，发展低成本高超声速飞行试验技术的重要性日益凸显[9]。

在自旋卫星利用RCS进行姿态控制方面，进动和章动并不同时控制。根据文献[10]：首先利用喷气机构产生横向控制力矩使卫星角动量进动至预定方向，再通过章动控制，使自旋轴与调整后的角动量方向重合。文献[10]以单脉冲控制为例阐明了章动控制基本原理，以双脉冲控制为例，阐明了进动控制基本原理，但没有针对实际工程问题中RCS多次作用下复杂的动力学演进过程进一步阐述。自旋卫星喷气控制对传感器和执行机构技术要求较高。根据文献[11]：自旋主动章动控制需要使用章动敏感器测量章动的相位和振幅。在固定推力喷气系统中，需要通过改变喷气时间的长度和两次喷气之间的间隔时间(也称喷气密度)，使系统处于脉冲调频调宽(PWPF[12])的工作状态。通过选择合适的喷气时刻(决定控制力矩的方向)和喷气持续时间(决定控制冲量的大小)，将角动量控制到任意方向。

在旋转导弹稳定和控制方面，国内外学者采用传统线性系统分析方法进行了大量研究[13-17]，由于本文RCS采用开关控制方式，旋转火箭是复杂的非线性控制系统，有关方法无法有效进行控制系统设计。文献[18]介绍了采用脉宽调制(PWM[19])技术设计RCS控制器对飞行器再入姿态控制的方法。该方法基于RCS的离散工作特性，首先把RCS当作连续力矩输出，在连续系统控制下进行姿态反馈律设计，然后再根据冲量矩等效原理，按照脉宽调制算法把连续的控制量调制成离散控制量，控制RCS产生不同脉冲宽度的离散力矩，以达到与连续力矩相同的控制效果，调制后的RCS冲量信号为一系列不同脉冲宽度信号。文献[20]介绍了利用RCS对高空旋转弹道导弹进行姿态控制的方法，RCS系统由6个喷管组成，产生俯仰、偏航、滚转3个方向控制力矩，通过自适应控制分配算法控制各个喷管开启时刻，采用PWM技术对控制冲量的大小进行调节。

综上所述，自旋卫星和自旋弹道导弹RCS控制具有以下特点：1)RCS系统技术要求高。通常由多个喷管组成，PWPF和PWM需要对脉冲宽度进行调节，对RCS频繁开启的可靠性和高速开关阀开关频率要求高。2)控制方法比较复杂。涉及多喷管开启策略，PWPF或PWM算法等。

本文针对高超声速试验火箭大气层外姿态控制问题，采用控制冲量不能调节的单个喷管作为执行机构，利用简单的开关控制实现高空旋转火箭掉头和再入姿态控制。通过旋转火箭在RCS间歇作用下的动力学过程分析，在“半联动”坐标系下推导了体现进动和章动综合效应的角速度状态变化递推公式，建立了横向角速度非线性控制模型；结合相平面内横向旋转角速度矢量运动和喷管控制规律，提出了系统稳定的必要条件；将“半联动”坐标系得到的俯仰、偏航运动规律应用于体轴系，构建了物理可实现系统进行了仿真校验。该方法可以满足我国低成本高超声速飞行试验火箭姿态控制。

1 旋转火箭的动力学特性分析

火箭熄火后在高空飞行，忽略气动力影响。自旋火箭在外力矩作用下呈现出复杂的陀螺效应，外力矩作用下自旋火箭的运动如图1所示。假定安装于尾部的喷管产生向上的推力，火箭一方面沿力矩方向进动，另一方面由于外力矩产生了俯仰角速度，火箭旋转角速度不再沿纵轴方向，导致火箭纵轴在空间做锥形摆动，该运动称为章动。定量描述旋转火箭在外力矩作用下的进动、章动效应是实现旋转火箭姿态控制的基础。

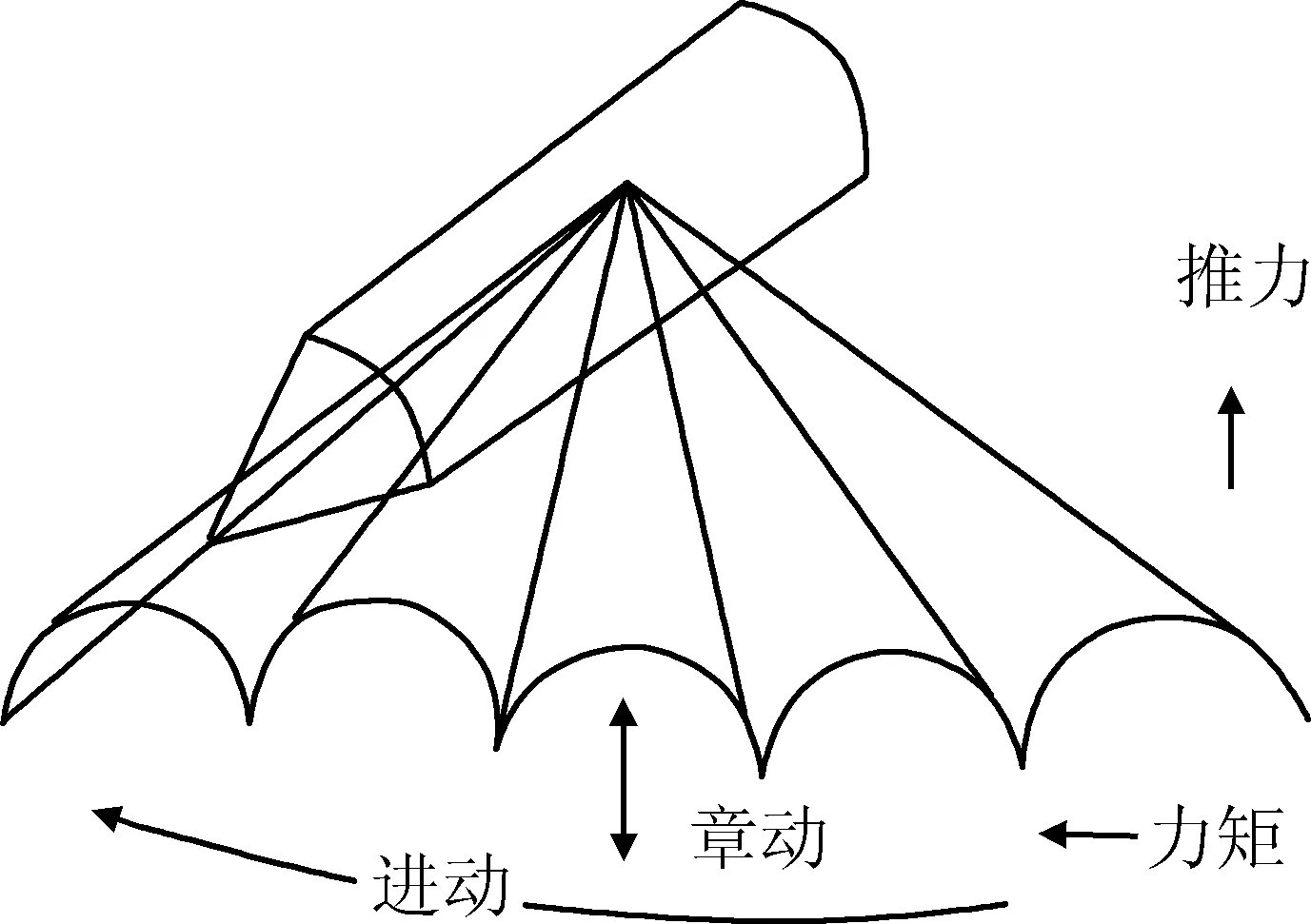
图1 在控制力矩作用下自旋火箭运动轨迹Fig. 1 Spinning rocket trajectory with control torque

1.1进动、章动效应分析

对于自旋火箭，我们并不关心其绕纵轴的旋转运动，只需要控制纵轴在空间的指向。刚体的姿态运动可以分解为绕三个体轴的旋转，如图2所示。刚体初始位置为o-x0y0z0，绕oz0轴旋转，沿箭头①到达o-x1y1z1位置；绕oy1轴旋转，沿箭头②到达o-x2y2z2位置；绕ox2轴自旋到达o-x3y3z3位置。由于不考虑对绕ox2的自旋，所以只考虑位置o-x2y2z2。这个位置仅随箭体纵轴的俯仰和偏航而变化，而自旋对其无影响。

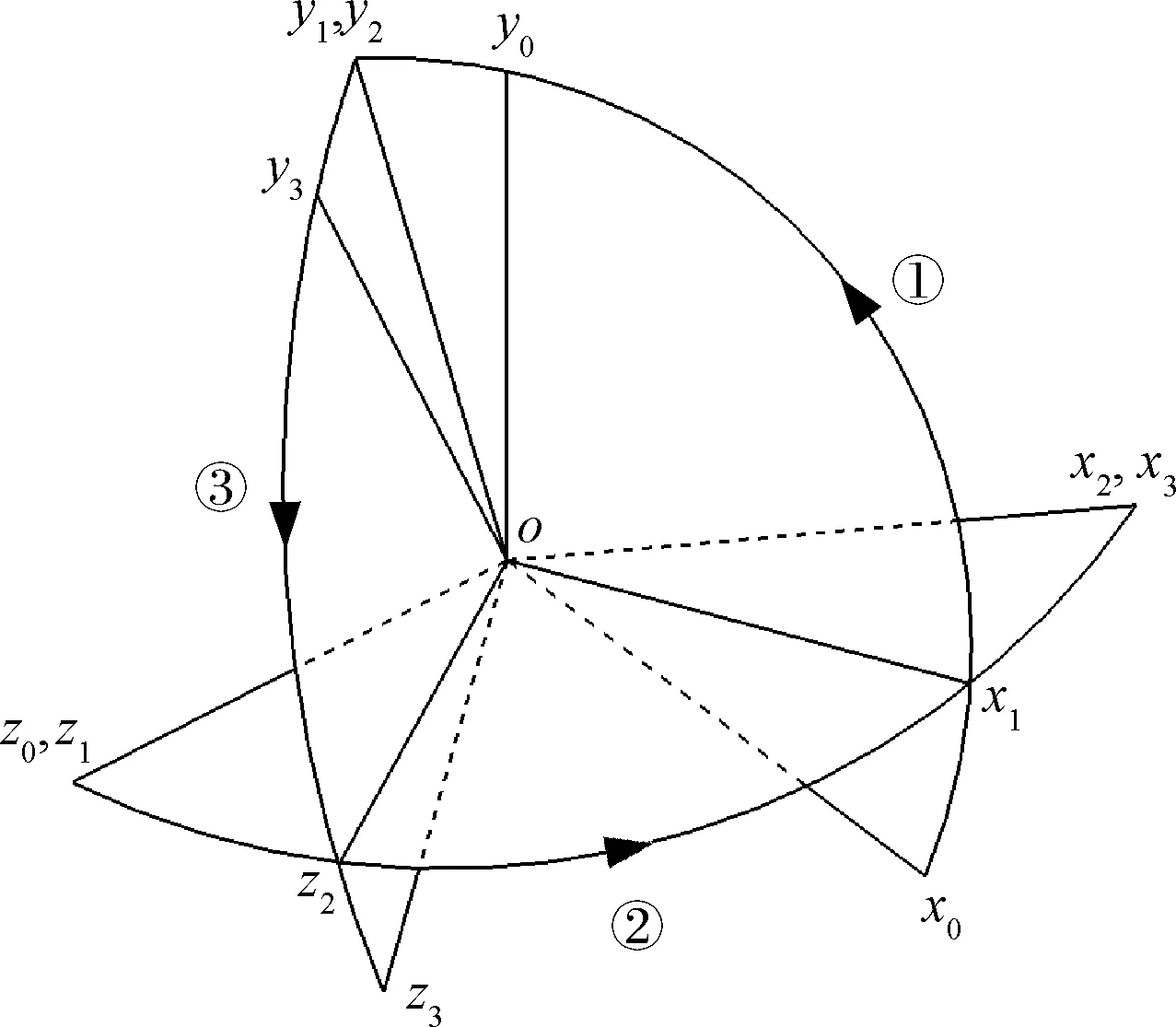
图2 坐标系相对关系Fig. 2 Rlative relationship of coordinate systems

建立质心为o的“半联动”坐标系o-xyz，始终追踪位置o-x2y2z2。在坐标系o-xyz中观察，箭体绕o-x轴自旋。但在惯性坐标系o-xyz并不随箭体自转。于是坐标系o-xyz旋转角速度矢量为：ω=[0,ωy,ωz]T。

由于火箭质量相对x轴对称分布，转动惯量张量可写为：

动量矩矢量在o-xyz中的表达：

H=[Ixωx,Iωy,Iωz]T

刚体绕质心转动的动量矩方程为：

(1)

将ω、H代入式(1)得：

(2)

[Mx,My,Mz]T是外力矩矢量在“半联动”坐标系中o-xyz的表达式。

假定ωx=const，则描述ωy和ωz的动力学方程为：

(3)

假定在t0时刻，箭体获得了横向角速度ωy 0、ωz 0，如图3所示。

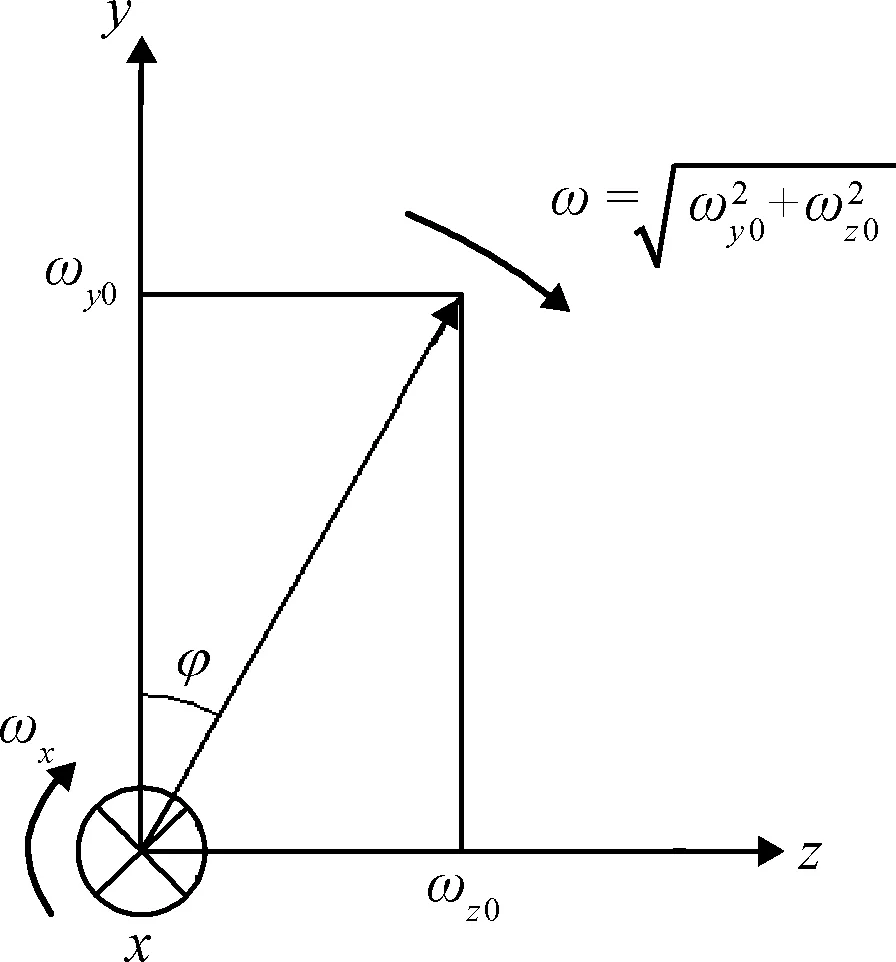
图3 箭体横向角速度矢量Fig. 3 Transverse angular rate vector of rocket

在随后的时间里，没有外力矩的作用，由方程(3)可得：

(4)

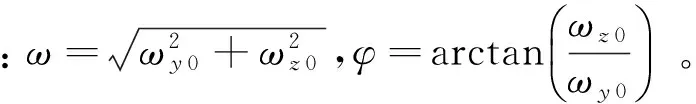
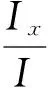
在箭体的底部安排一个喷管，如图4所示。喷管随箭体绕o-x轴旋转。当喷管在阴影区域Ⅰ开启时，产生的力矩位于阴影区域Ⅱ：以相角χ为中心，宽度为2α的扇形区域。

以喷管处于左边水平位置时刻作为计时起点，在τ时刻，喷管转到相角φ处：

φ(τ)=ωxτ,χ-α≤φ(τ)≤χ+α

此时刻推力产生的横向力矩位于阴影Ⅱ中的箭头处，设推力矩大小恒为T。经过一个微元时间dτ，刚体获得一个位于箭头处的横向角速度矢量增量：Tdτ/I,相角为φ(τ)=ωxτ。当时间推进到t时刻，该横向角速度矢量增量发展为：

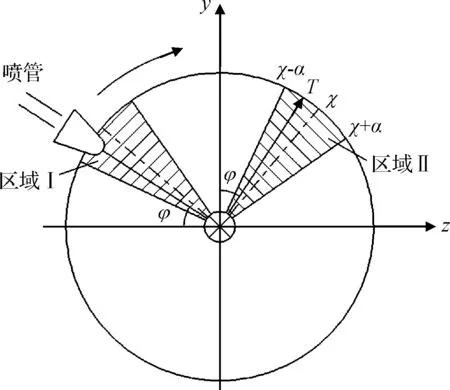
图4 喷管及力矩工作区间Fig. 4 Operation area of nozzle and torque

在t时刻，刚体受横向力矩产生的角速度是所有这些微元角速度增量演化的叠加：

(5)

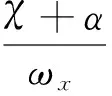
(6)

计算出式(6)的积分得：

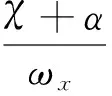
(7)

式(7)仅仅是箭体受到喷管推力横向力矩后产生的角速度。若在初始时刻t0，刚体具有初始横向角速度ωy 0、ωz 0,还需叠加上式(4)描述的角速度演进。可得：

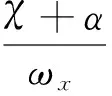
(8)

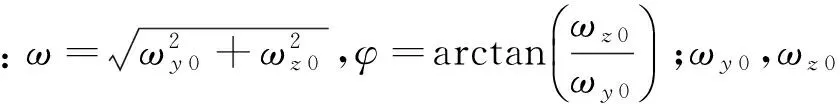
1.2喷管间歇开启动力学过程分析

对于旋转箭体，我们的目标是控制它达到目标俯仰角θT，同时偏航角ψT为零。

控制方式见图5。采用安装在箭体底部的喷管产生需要的控制力矩。

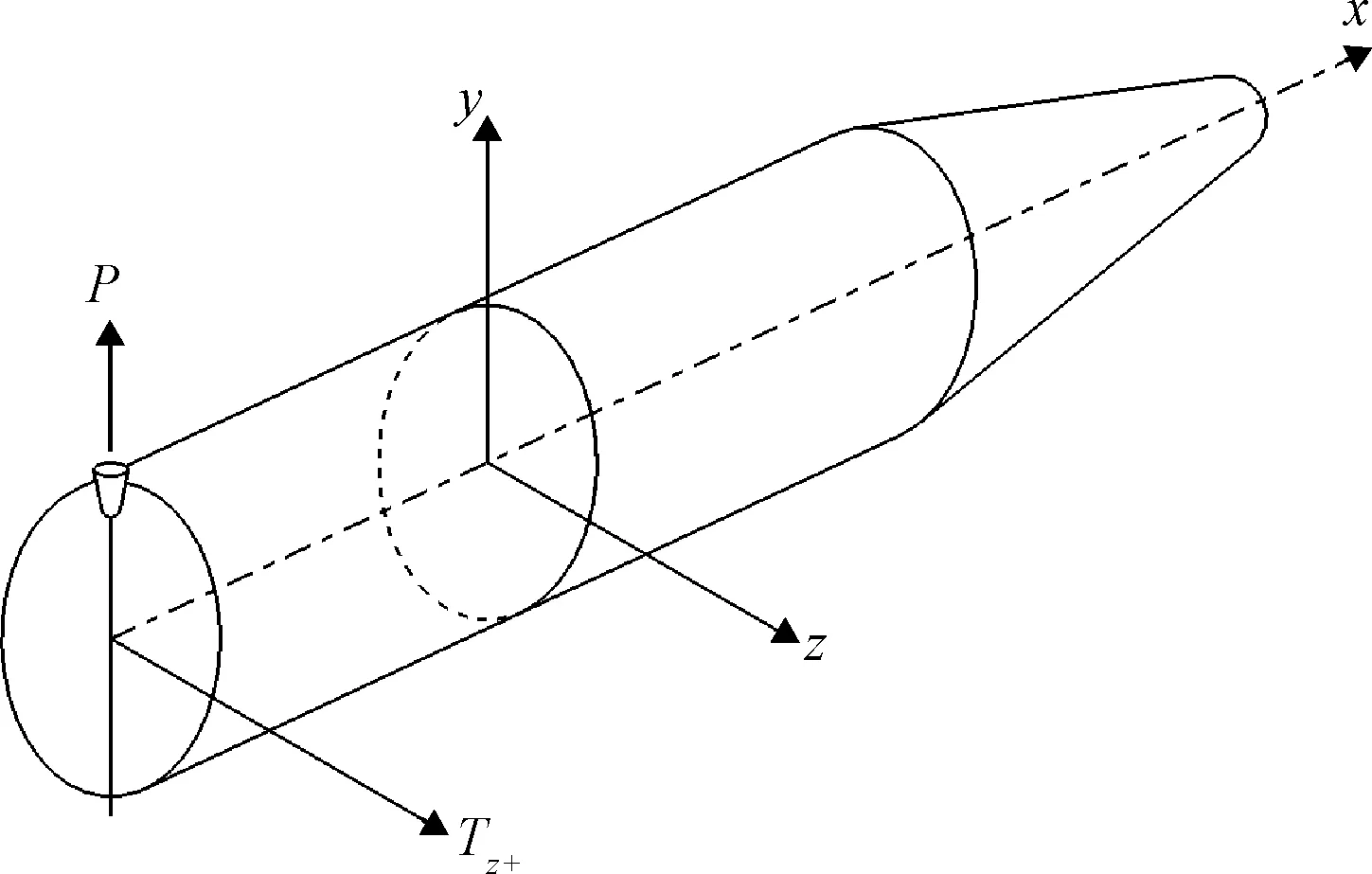
图5 喷管在箭体上的位置Fig. 5 Mounting position of the nozzle on the rocket

单个喷管随箭体旋转，可以产生任意方向的横向控制力矩。为简化控制逻辑，规定喷管只在俯仰、偏航方向开启。

如图6所示，当喷管转到位置P0时，若决定在其后的2α扇形区域内开启，那么产生的力矩位于图中阴影区域，主要产生抬头力矩，计为Tz+。

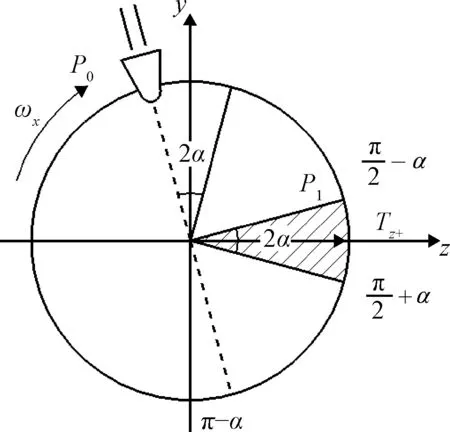
图6 喷管在y轴正向区域作用产生的力矩Fig.6 The generated torque of the nozzle toward the positive y-axis

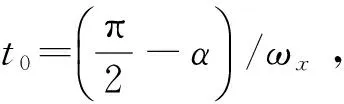
下一次决定喷管是否开启的位置为P1，对应时刻为t1=(π-α)/ωx。

假设喷管在位置P0时，偏航、俯仰角速度分别为ωy 0,ωz 0，则由式(8)，当喷管转到位置P1时偏航、俯仰角速度分别为：

(9)

式中：

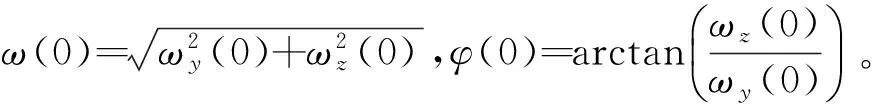
当喷管分别在位置P1、P2、P3，角度为2α的扇形区间开启，产生的力矩如图7～9所示。由式(8)推导可得喷管转至位置P2、P3、P0时的偏航、俯仰角速度如式(10)～(12)所示。

图7 喷管在z轴正向区域作用产生的力矩Fig. 7 The generated torque of the nozzle toward the positive z-axis

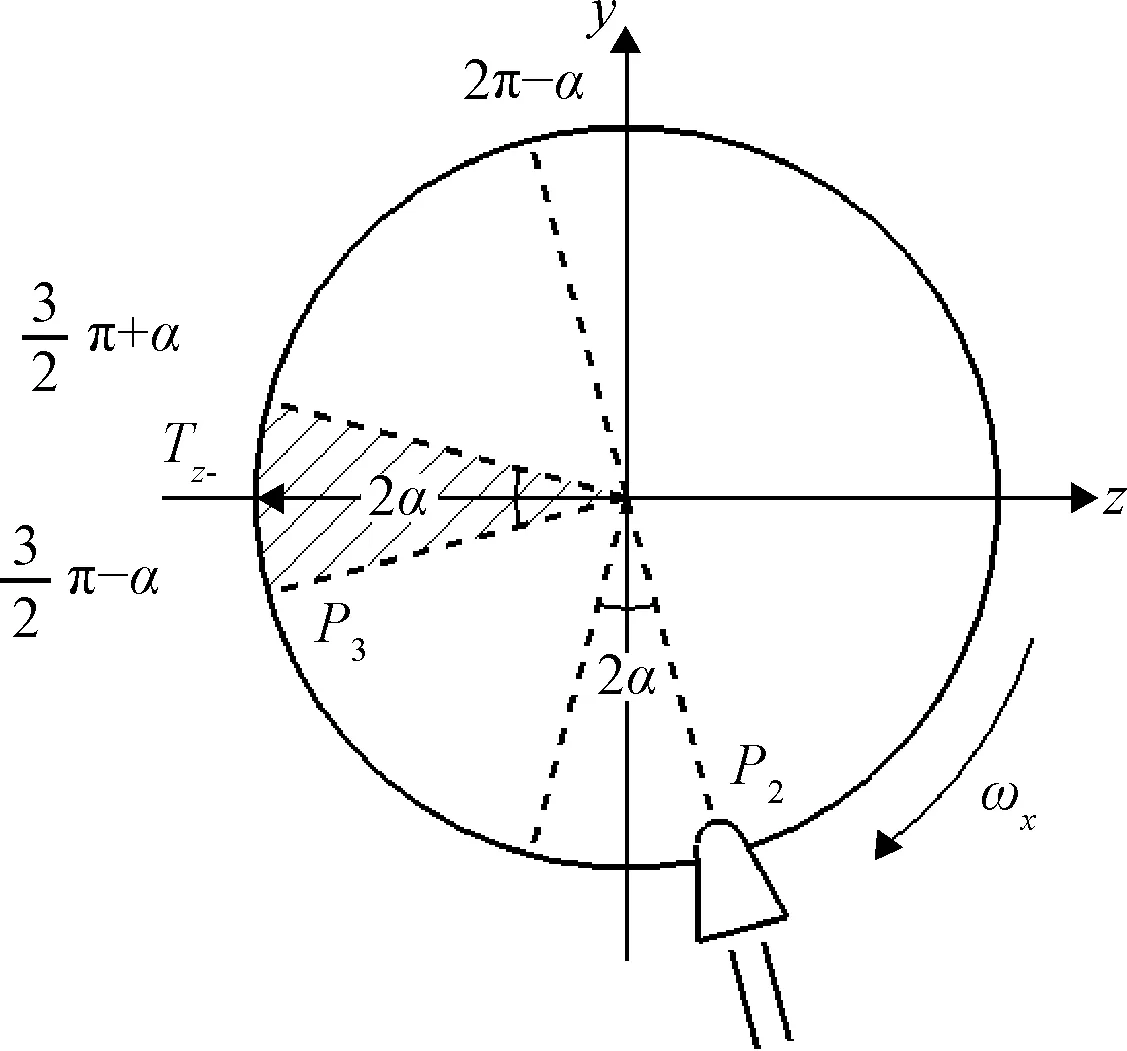
图8 喷管在y轴负向区域作用产生的力矩Fig. 8 The generated torque of the nozzle toward the negative y-axis

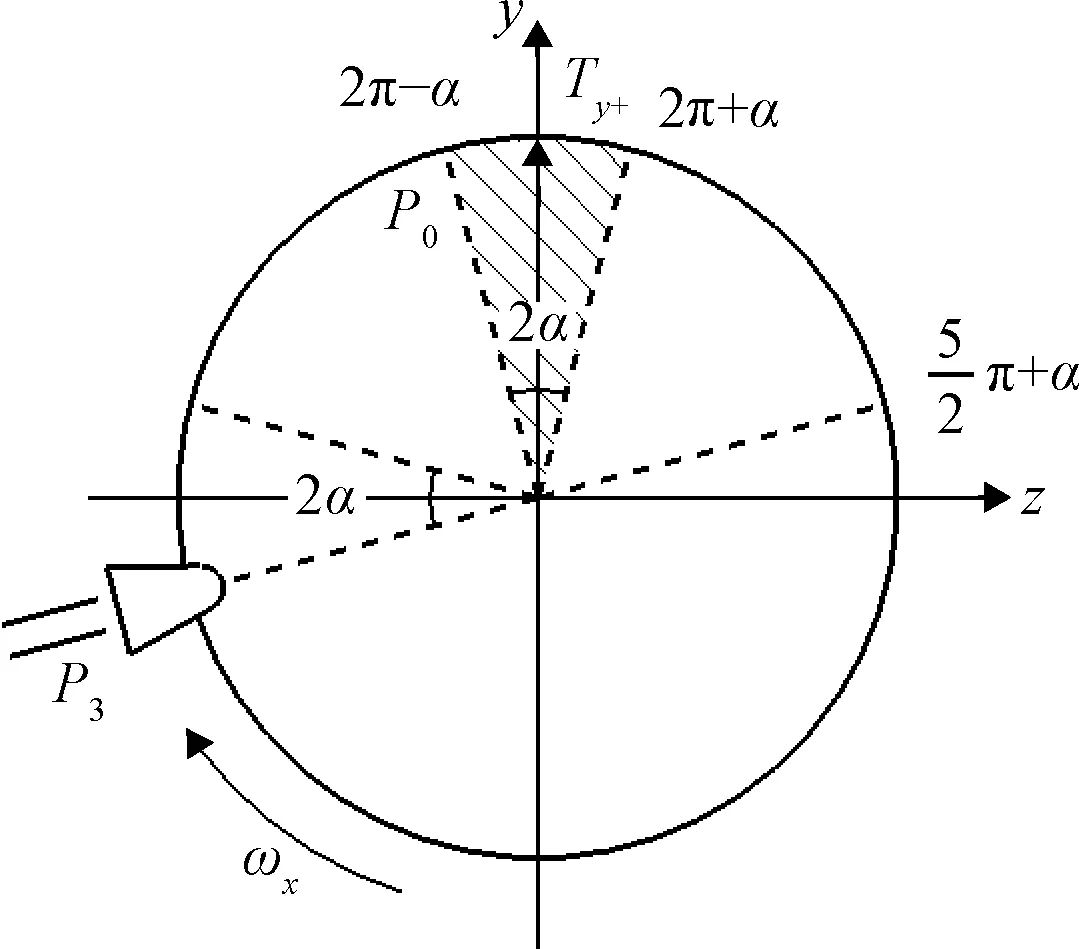
图9 喷管在z轴负向区域作用产生的力矩Fig. 9 The generated torque of the nozzle toward the negative z-axis

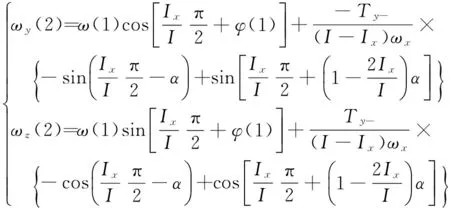
(10)

式中：

(11)

式中：

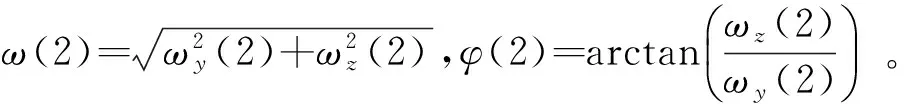
(12)

式中：

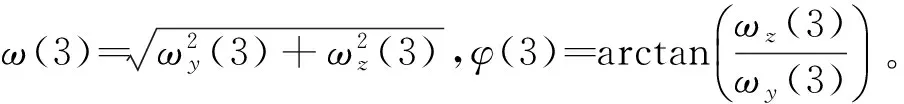
上述过程可用离散时间数学模型描述，状态变化的递推公式为：

王剑波先生：汽车新四化风起云涌，这给康宁带来了巨大的挑战与机遇。对于汽车玻璃而言，主机厂提出了更高的要求，比如更高的光学指标，更轻更坚固的物理指标。这些恰好是大猩猩玻璃的强项。我们参与汽车玻璃市场开始于2013年，目前已经和超过25家主机厂进行深度合作，服务的汽车品牌超过50个。我们的产品主要分为三类：“汽车内饰”，即仪表中控和娱乐系统的玻璃面板；“外饰”，即汽车风窗玻璃和车门玻璃；“未来”，即面向未来的产品研发。因为这些项目还没有量产，所以今天就不和大家分享了。

(13)

式中：

将式(13)展开，系统以状态方程形式描述为：

(14)

2 控制方案

2.1喷管开启逻辑

归纳第1.2节分析过程，得到在4个位置开启时偏航和俯仰角速度增量Δy、Δz。

1)当喷管从P0到P1时：

[Δy,Δz]=[-u,v]

(15a)

2)当喷管从P1到P2时：

[Δy,Δz]=[-v,-u]

(15b)

3)当喷管从P2到P3时：

[Δy,Δz]=[u,-v]

(15c)

[Δy,Δz]=[v,u]

(15d)

式中：

(16)

若喷管开启S=1；否则S=0。若α是个小量，则：

(17)

上述4种情况对应的角速度增量[Δy,Δz]的方向分别如图10～13所示。

由于喷管是在旋转状态下产生推力矩，因此每次喷管作用产生的角速度增量并不正好沿y轴、z轴，而是存在一个小的偏量u，由于u是小量，可以利用的控制输入量是v。喷管在P0、P2、P3、P1四个区域开启分别提供俯仰、偏航角速度正负方向4个维度的控制输入，这是实现控制所需的最小维度。

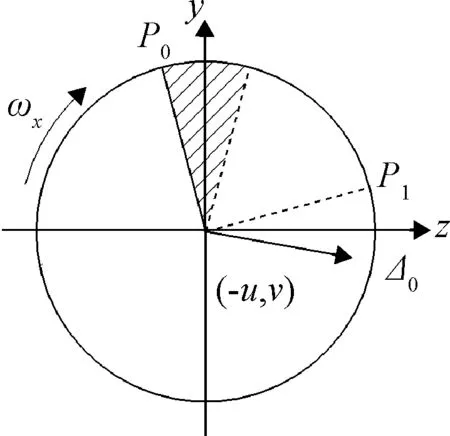
图10 P0处开启，P1处采样Fig. 10 Turn on at P0,sample at P1

图11 P1处开启，P2处采样Fig. 11 Turn on at P1,sample at P2

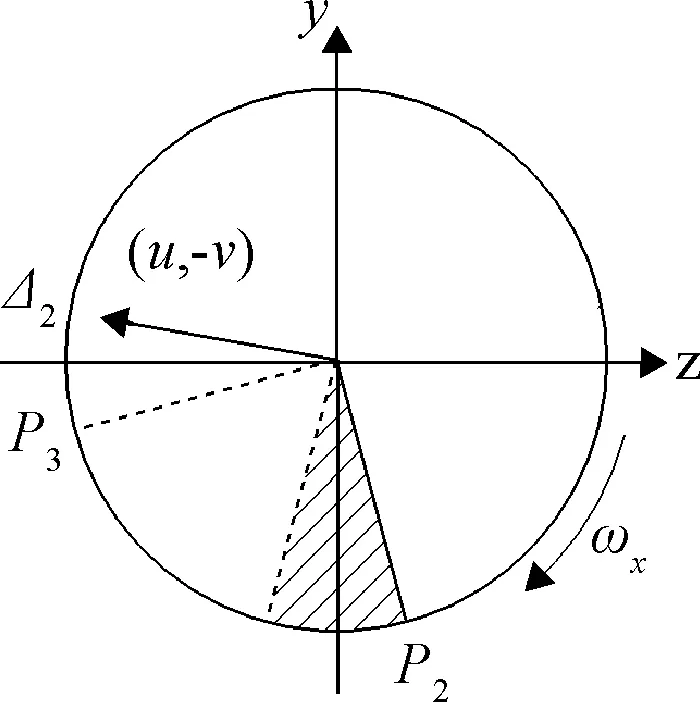
图12 P2处开启，P3处采样Fig. 12 Turn on at P2,sample at P3

如果给定一个目标角速度ωzT，希望箭体以ωzT做俯仰运动，同时保持偏航角速度为零。由图10～13所示喷管在4个位置开启时产生的角速度增量v的方向，得到喷管开启条件：

1)当喷管位于P0时系统采样，若ωzT-ωz>0，则喷管开启(S=1)，增大ωz。否则喷管不开启(S=0)。

图13 P3处开启，P0处采样Fig. 13 Turn on at P3,sample at P0

2)当喷管位于P1时系统采样，若0-ωy<0，则喷管开启(S=1)，减小ωy；否则喷管不开启(S=0)。

3)当喷管位于P2时系统采样，若ωzT-ωz<0，则喷管开启(S=1)，减小ωz；否则喷管不开启(S=0)。

4)当喷管位于P3时系统采样，若0-ωy>0，则喷管开启(S=1)，增大ωy；否则喷管不开启，(S=0)。

为了避免箭体的横向角速度在目标值处上下频繁跳动，引入一个死区宽度ε。初步设计时取ε=v/2,通过仿真确定ε，使系统达到好的动态特性。

横向角速度系统控制原理见图14。这是一个非线性控制系统，要用解析法分析并不容易。可用“相平面”法来分析。建立如图15所示的ωy-ωz平面，箭体的横向旋转角速度可在相平面用一个始于原点的向量来表示。

图14 横向角速度控制原理Fig. 14 The schematic diagram of transverse angular rate control

图15 在相平面表示的箭体横向旋转角速度矢量Fig. 15 The sketch of transverse angular rate on the phase plane

(18)

同理当喷管转到如图12所示位置P2,考察喷管旋转一周对应ωy在相平面内的变化,同样推导可得：

(19)

式(18)～(19)为系统稳定的必要条件。

2.2姿态控制方案

根据“半联动”坐标系和欧拉角θ、ψ(俯仰角、偏航角)的定义，在ψ较小时，可以得到如下关系：

(20)

因此在偏航角较小的条件下，“半联动”坐标系有关结论适用于体轴系。

前述讨论都是针对箭体横向角速度的控制，但最终追求的是对箭体姿态的控制。为此，需要在图14的基础上增加一个外回路，并将“半联动”坐标系推导的俯仰、偏航运动规律应用于体轴系O-x1y1z1。为此构建如图16所示的物理可实现系统，该系统通过对箭体姿态角和欧拉角角速率反馈实现俯仰角和偏航角控制。图中约定喷管安装于y1正方向，在体轴系中，喷管开启时只产生沿z1正方向的力矩Mz1，喷管随箭体旋转产生俯仰、偏航控制力矩。

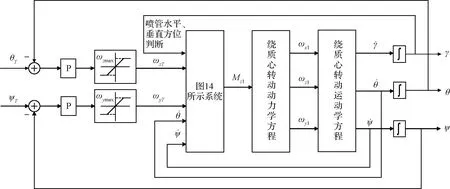
图16 姿态控制原理Fig. 16 The schematic diagram of attitude control

为了满足稳定条件(18)、(19)，在图16中对ωy,ωz限幅：

(21)

式中：0<ξ<1。

图16中外回路由俯仰角和偏航角误差得到目标角速度。俯仰、偏航通道的P采用比例控制算法：

(22)

内回路通过滚转角确定喷管转动位置，通过俯仰角速度、偏航角速度与目标角速度的误差控制喷管开启。

控制过程中RCS喷管一方面使自旋轴向目标方向进动，另一方面不断减小自旋轴在空间的圆锥运动,逐渐将自旋轴控制到目标方向。

3 仿真校验

为校验该方法的有效性，以俯仰角控制为例进行仿真。初始条件：ωy0=10°/s，ωz 0=10°/s，θ0=10°；控制目标：θT=-60°；转动惯量：Ix=7.55 kg·m2，I=110.65 kg·m2；喷管力矩T=1000.0 N·m，约定喷管作用区间2α=30°。

在控制参数(ξ,ε)固定的情况下，图17、图18分别提供了喷管在约定值(2α=30°)和偏离约定值(2α=22°)两种情况下，箭体以不同角速度(ωx=2.0、3.0、4.0 r/s)自旋的仿真结果。图19提供了ωx=3.0 r/s，α=15°情况下RCS喷管开启历程。

图17 俯仰角历程(2α=30°)Fig. 17 The curve of pitch vs. time(2α=30°)

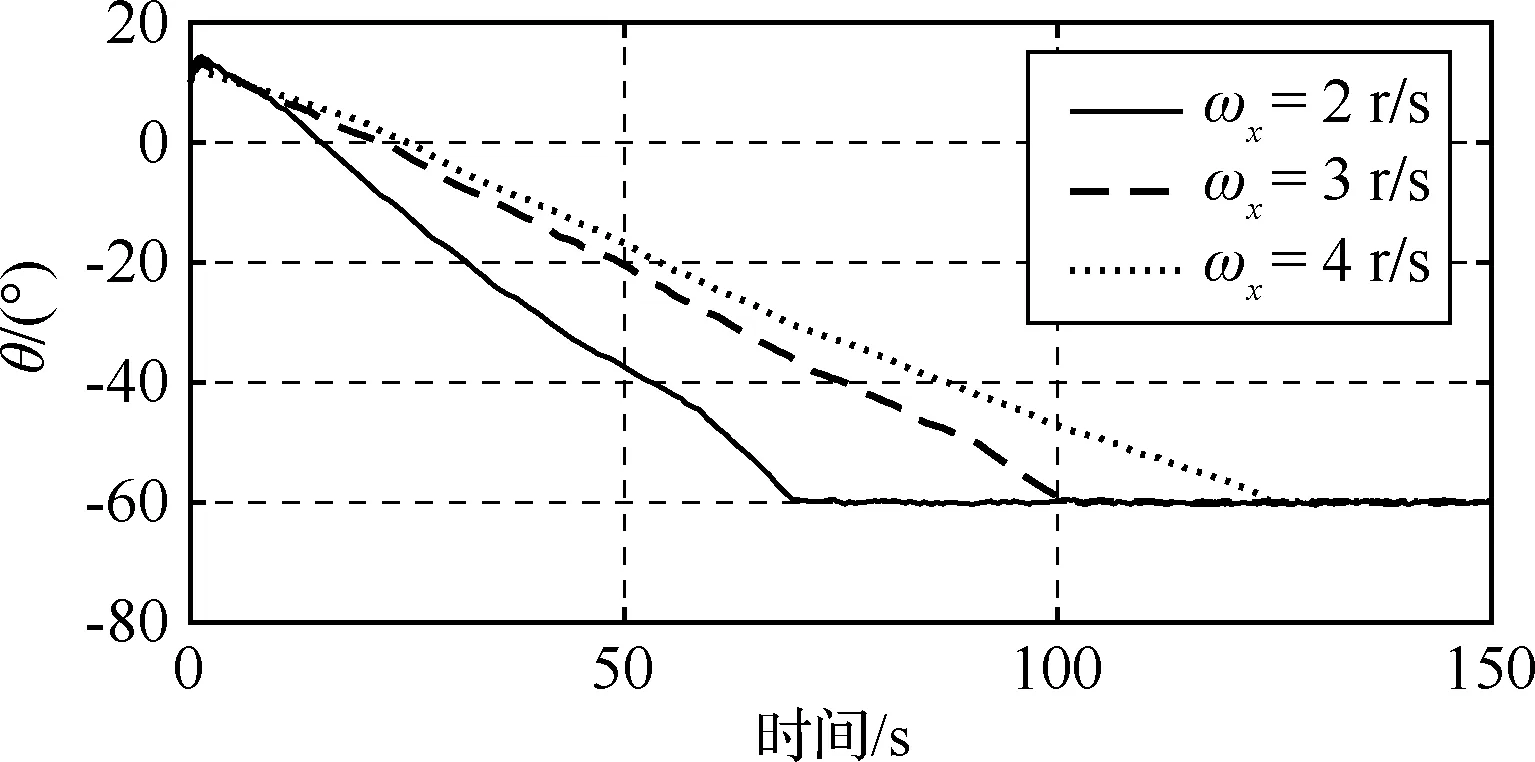
图18 俯仰角历程(2α=22°)Fig. 18 The curve of pitch vs. time (2α=22°)

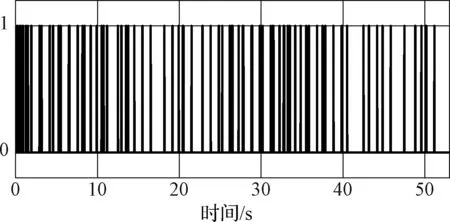
图19 RCS喷管开启历程(ωr=3 r/s,α=15°)Fig. 19 The on-off processes of RCS nozzle (ωr=3 r/s,α=15°)

仿真结果表明：仅仅依靠产生固定控制力矩的单个喷管进行开关控制，在RCS喷气冲量矩(转速一定)相对误差26.7%，并且自旋角动量差别较大的情况下(自转角速率2.0 r/s～4.0 r/s)，仍然可以有效控制。说明控制方法具有良好鲁棒性，对RCS喷管的精度要求较低。

4 结 论

1)控制方法简单、有效。通过对单个喷管的开关控制实现高空旋转火箭的掉头和姿态控制。控制方法鲁棒性较好，可以适应一定范围自转角速度变化。

2)对硬件系统的技术指标要求较低。RCS仅一个喷管，喷射冲量不需调节且允许误差较大，降低了喷管和高速开关阀的技术指标；传感器可采用捷联惯性导航系统提供所需的反馈信号；由于控制方法简单，计算机配置要求较低。

3)后续将进一步研究利用四元数来描述旋转火箭姿态，解决以-90°左右姿态再入时运动方程出现奇点的问题。

4)结合地面仿真调试，该方法可以应用于低成本高超声速试验火箭高空姿态控制。

[1] Dolvin D J. Hypersonic international flight research and experimentation (HIFiRE) fundamental sciences and technology development strategy[R]. AIAA 2008-2581.

[2] Bowcutt K, Paull A, Dolvin D J, et al. HIFiRE: an international collaboration to advance the science and technology of hypersonic flight[C]. The 28th International Congress of the Aeronautical Sciences, Brisbane, Australia,September 23-28,2012.

[3] Dolvin D J. Hypersonic international flight research and experimentation technology development and flight certification strategy [C]. The 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, October 19-22, 2009.

[4] Franze M. SHEFEX II-an aerodynamic and structural post-flight analysis[C]. AIAA Atmospheric Flight Mechanics Conference, Washington, USA, June 13-17,2016.

[5] José M A Longo. Present results and future challenges of the DLR SHEFEX program[R]. AIAA 2009-7226.

[6] Hass N E, Smart M K, Paull A. Flight data analysis of HyShot 2[R]. AIAA 2005-3354.

[7] Smith T R, Bowcutt K G. HIFiRE 4: a low-cost aerodynamics, stability, and control hypersonic flight experiment[C]. The 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, USA, April 11-14, 2011.

[8] Kimmel R L, Adamczak D, Berger K, et al. HIFiRE-5 flight vehicle design[C]. The 40th Fluid Dynamics Conference and Exhibit, Chicago, USA, June 28-July 1, 2010.

[9] 陈广强, 王贵东, 陈冰雁, 等. 低成本飞行试验平台的FADS技术研究[J]. 宇航学报, 2015, 36(10): 1195-1202. [Cheng Guang-qiang, Wang Gui-dong, Chen Bing-yan, et al. Study of flush air data sensing system technology for low cost flight test platform [J]. Journal of Astronautics, 2015, 36(10): 1195-1202.]

[10] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998: 234-237.

[11] 屠善澄. 卫星姿态动力学与控制[M]. 北京: 宇航出版社, 2001: 401-427.

[12] 王清, 杨宝庆, 马克茂. 一种优化PWPF 调节器在动能拦截器末制导中的应用研究[J]. 宇航学报, 2005, 26(5): 576-580. [Wang Qing, Yang Bao-qing, Ma Ke-mao. PWPF optimizing design and its application research to terminal guidance of kenetic killing vehicle [J]. Journal of Astronautics, 2005, 26(5): 576-580.]

[13] Morote J, Liano G. Analysis of control and guidance of rolling missiles with a single plane of control fins [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, American, August 14-17, 2000.

[14] 任天荣, 马建敏. 基于陀螺力学的旋转导弹锥形运动分析[J]. 宇航学报, 2010, 31(9): 2082-2087. [Ren Tian-rong, Ma Jian-min. Coning motion analysis of spinning missile based on gyrodynamics [J]. Journal of Astronautics, 2010, 31(9): 2082-2087.]

[15] 闫晓勇, 杨树兴, 张成. 基于章动运动理论的火箭弹锥形运动稳定性分析[J].兵工学报, 2009, 30(10): 1291-1296. [Yan Xiao-yong, Yang Shu-xing, Zhang Cheng. Analysis of stability for coning motion of rockets based on theory of nutation movement [J]. Acta Armamentii, 2009, 30(10): 1291-1296.]

[16] 周凤岐, 易彦, 周军. 克服旋转导弹螺旋运动的方法研究[J]. 宇航学报, 2001, 22(5):77-81. [Zhou Feng-qi, Yi Yan, Zhou Jun. Research on overcoming the coning of rotary missile [J]. Journal of Astronautics, 2001, 22(5): 77-81.]

[17] 王华毕, 吴甲生. 火箭弹锥形运动稳定性分析[J]. 兵工学报, 2008, 29(5): 562-566. [Wang Hua-bi, Wu Jia-sheng. The coning motion stability analysis of rocket [J]. Acta Armamentii, 2008, 29(5): 562-566.]

[18] 周宇，黄一敏，孙春贞. 基于脉宽调制的反作用控制系统技术[J]. 信息与电子工程, 2012, 10(4): 446-450. [Zhou Yu, Huang Yi-min, Sun Chun-zhen. Control technology based on pulse width modulation of RCS [J]. Information and Electronic Engineering, 2012, 10(4): 446-450.]

[19] 郭正雄, 张珩, 肖歆昕, 等. 地球大气边缘高超声速飞行再入点调整方法[J]. 宇航学报, 2013, 34(7): 946-954. [Gou Zheng-xiong, Zhang Heng, Xiao Xin-xin, et al. Adjustment method of re-entry position for hypersonic flight at edge of earth’s atmosphere [J]. Journal of Astronautics, 2013, 34(7): 946-954.]

[20] Ricardo E, Juan V N. Active nutation & precession control for exoatmospheric spinning ballistic missiles [C]. AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, USA, August 18-21, 2008.

AttitudeControlofLow-CostRocketsforHypersonicResearchFlightTests

WU Dong-sheng1, ZHENG Zhong-pei2, DING Zhi-jian1

(1.Airbreathing Hypersonic Technology Research Center, China Aerodynamics Research and Development Center, Mianyang 621000, China;2.Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China)

To meet the requirements of the low-cost rockets for hypersonic flight tests, a synchronized control scheme is proposed for controlling the procession and nutation of a rocket through a simple reaction control system (RCS), which can achieve the large-scale attitude adjustment and reentry control. The RCS consists of a single nozzle with nonadjustable duration of jet-flow. Firstly, the spinning rocket dynamic processes with the control of RCS are analyzed. Then the system models and the stability conditions, which show the coupled effects of precession and nutation, are established. Finally, the RCS control strategy is designed with the help of the attitudes and the angular rate information. Moreover, the control strategy can make the rocket attitudes meet the demands. The theoretical simulation results demonstrate that the large-scale adjustment of the pitch angle (+10°～-60°) can still be achieved under the condition that the relative error of RCS impulsive moment is 26.7% and the variation range of spin angular rate is 2.0～4.0 r/s. This method is applicable to the low-cost rockets for hypersonic flight experiments, and promotes the development of the extensive flight experiments for hypersonic research.

Hypersonic; Spinning rocket; Attitude control; Reaction control system (RCS); Precession; Nutation

V448

A

1000-1328(2017)09- 0946-10

10.3873/j.issn.1000-1328.2017.09.007

2017- 01-22;

2017- 06-29

吴东升(1964-)，男，硕士，高级工程师，主要从事高超声速模型飞行试验研究。

通信地址：四川省绵阳市二环路南段6号19信箱01分箱(621000)

电话: 13778019695

E-mail: hardwudongsheng@sina.com