面向任务约束的航天器姿控系统在轨重构算法

陈嘉文，程月华，姜 斌，陆宁云，杨天社

(1.南京航空航天大学自动化学院，南京 211106；2. 南京航空航天大学航天学院，南京 210016；3. 约克大学机械工程系，多伦多M3J 1P3；4. 航天器故障诊断与在轨维修重点实验室，西安 710043)

面向任务约束的航天器姿控系统在轨重构算法

陈嘉文1，程月华2,3，姜 斌1，陆宁云1，杨天社4

(1.南京航空航天大学自动化学院，南京 211106；2. 南京航空航天大学航天学院，南京 210016；3. 约克大学机械工程系，多伦多M3J 1P3；4. 航天器故障诊断与在轨维修重点实验室，西安 710043)

针对任务约束下的航天器姿态控制系统(ACS)在轨重构问题，提出了一种基于自适应动态规划(ADP)的在轨重构算法。首先，综合考虑航天器在轨任务约束条件设计效用函数和性能指标函数，获得离散Hamilton-Jacobian-Bellman(HJB)方程形式的最优重构策略。其次，采用执行依赖启发式动态规划(ADHDP)方法近似求解HJB方程，避免了直接求解HJB方程的“维数灾难”问题。通过简化设计ADHDP执行网络，提高了迭代训练速度；同时在训练中引入ε-greedy因子，避免了训练算法过早陷入局部最优解。仿真结果验证了所提方法的有效性。

姿态控制系统(ACS)；在轨重构；任务约束；自适应动态规划(ADP)

0 引 言

随着航天技术的进步以及在轨运行航天器数量的不断增加，及时发现故障，并采取合理措施，确保航天器的安全稳定运行，已成为航天器在轨管理的重点[1-3]。航天器地面可观测弧段有限，在轨卫星一旦发生故障，平台失稳，即使只有几分钟、十几分钟，都可能会导致整个飞行任务的失败[4]。为确保航天器在轨任务顺利实施，姿态控制系统应具备自主在轨重构能力。在轨重构控制不但可以增强航天器的故障应对能力，降低地面测控人力物力成本，还可以提高其任务完成能力，最大化利用平台资源。

目前，国内外已有许多针对航天器姿态重构控制技术的研究。文献[5]考虑系统资源、性能等多约束条件，建立了基于组合赋权法的卫星可重构性综合评价方法。文献[6]提出了一种基于交互式多模型(IMM)的卫星姿态控制系统故障检测与诊断(FDD)方法。文献[7]采用IMM算法获得故障位置和模型，同时利用特征结构配置进行重构控制，实现了卫星姿控系统FDD与控制重构的整合设计。文献[8]针对反作用飞轮故障提出了一种故障检测与恢复方案，先采用状态空间法和非线性参数神经网络(NLPNN)辨识未知故障，再将故障估计结果应用于重构控制器。

现有成果大多聚焦于容错控制器设计，利用系统的解析冗余关系，采用基于模型的方法重构控制器从而达到容错目的[9]。而基于任务约束的航天器故障系统重构控制鲜有研究。对于在轨航天器而言，故障情况下系统所处的工作状态及工作模式不同，其控制系统的重构决策应区别对待[10]。在系统按预定计划实施重要科学任务时，发生微小故障，若系统不顾当前任务约束，武断实施系统重构，则会因此改变系统状态，也许造成资源浪费，甚至带来负面影响。而在有些故障情形下，需要对故障进行危害评估，若不及时有效处理故障，则可能会因为故障在系统传播而导致系统控制性能恶化，甚至威胁平台的安全性。为此，系统在轨重构控制需要综合考虑任务约束和系统配置等因素，根据系统当前状态信息，实现自主最优决策，减小航天器与地面进行信息交互的代价，提高其任务完成能力和故障应对能力[11-12]。

本文将针对执行机构故障情况下的航天器姿态控制系统，采用自适应动态规划(Adaptive dynamic programming，ADP)算法，研究基于在轨任务约束下的重构控制技术，旨在为航天器在轨重构提供有效的实施手段和理论支持。自1977年Werbos[13]首次提出ADP方法以来，该方法获得了越来越广泛的关注，已成为计算智能领域的一大研究热点[14]。ADP基于增强学习的思想，采用迭代学习算法训练人工神经网络以近似求解Hamilton-Jacobian-Bellman(HJB)方程，避免了传统动态规划方法“维数灾难”的问题，是一种解决高维复杂系统最优控制问题的有效方法[14-17]。本文综合考虑航天器在轨任务约束条件设计效用函数和性能指标函数，评估比较故障情形下不同重构方案的优劣，获得离散 HJB方程形式的最优重构策略。针对HJB方程难以精确求解的问题，采用执行依赖启发式动态规划(Action-dependent heuristic dynamic programming, ADHDP)方法获得HJB方程的近似解，得到故障情况下基于系统当前状态和任务约束的最优在轨重构策略。

1 在轨重构约束条件

为了满足高可靠性的要求，航天器姿态控制系统在设计时通常了采用硬件功能冗余设计。功能冗余系统通过不同硬件组合，形成多种配置方案，不同配置方案的实施代价各有差异。故障情况下，需要根据故障情况和实际需求，实现姿态控制系统的最优重构。在轨重构系统结构如图1所示。

图1 在轨重构系统结构Fig.1 The on-orbit reconfiguration system structure

在轨重构模块主要包括两个部分：在轨重构决策模块和在轨重构执行模块。在故障发生后，在轨重构模块根据故障诊断结果和任务约束条件，确定一个系统重构指令序列，恢复航天器姿控系统的性能，从而继续执行既定任务；在无法继续执行任务的情况下，终止任务的执行并进入安全模式，等待地面测控人员介入处理。故障情形下，姿态重构控制与任务目标密切相关。姿控系统的重构以任务实施为设计目标，设计约束包括以下几个方面：

1)精度约束：空间科学任务的执行对航天器平台指向精度有特定要求。如对地成像任务，对航天器对地指向姿态、稳定度需在限定范围内。

2)控制能耗约束：星载能源有限，蓄电池充放电周期受轨道光照及地影影响，推进剂类消耗型能源星载携带亦十分有限。控制能耗是制约系统重构及任务实施的重要约束因素。

3)任务优先级约束：对于优先级高的任务，需以任务的实施为最高目标，适当放宽能耗约束；对于某些特殊任务，甚至可以不顾平台安全性坚持执行任务。而对于一些优先级低的任务，则应优先保障平台安全性，实施系统重构，选择放弃当前任务。

在轨重构系统旨在实现任务约束下的最优重构决策。当系统故障发生后，在轨重构模块利用故障诊断模块提供的故障信息，综合指向精度、控制能耗、任务优先级等约束条件做出最优重构决策，使系统恢复到可以执行任务的控制性能，并且满足任务约束条件；在无法继续执行任务的情况下，终止任务的执行并进入安全模式，等待地面测控人员介入处理。

2 自适应动态规划

本节将对系统状态进行定义，并设计在轨重构的效用函数和性能指标函数，获得最优重构策略的HJB方程；然后给出近似求解HJB方程的ADHDP方法。

2.1系统状态与性能指标函数

系统状态是在轨重构模块进行决策的依据。重构模块从故障发生时刻开始决策，设重构决策窗口长度为W，决策周期为T，则整个决策窗口可以划分为N=W/T个时间段。将系统状态sk∈S定义为

(1)

在轨重构决策模块的输出动作ak定义为

(2)

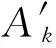
(3)

在第k时刻，在轨重构模块根据系统状态sk选择并执行最优重构策略ak，系统随之转移到状态sk+1，在轨重构模块再执行ak+1…重复此过程，便得到一个动作序列{ak,ak+1,…,aN}。在轨重构模块的任务便是贯序决策问题，确定一个策略π:S→A，它基于当前观察到的状态sk选择下一步动作ak，即π(sk)=ak。最优的重构策略应在任务约束下具有最优性能指标。性能指标函数定义为

(4)

式中：γ折扣因子，满足0<γ≤1；U(sk,ak)为ADP方法的效用函数，表示在sk状态下执行动作ak的代价。效用函数U(sk,ak)定义为

U(sk,ak)=αE(sk,ak)+βC(sk,ak)+λρG(sk,ak)

(5)

式中：E(sk,ak)为控制误差项；C(sk,ak)为控制能耗项；G(sk,ak)为任务执行项；α,β,λ为常数权值；ρ∈{1,2,3,4,5}为任务优先级，ρ越大，任务越重要。

控制误差项E(sk,ak)和控制能耗项C(sk,ak)分别定义为

(6)

式中：Q和R为正定矩阵；e(τ)=x(τ)-r(τ)为系统姿态x(τ)与期望姿态r(τ)之间的误差；u(τ)为控制输入。

任务执行项G(sk,ak)定义为

(7)

注2. 姿态信息xk并不直接用于计算效用函数U(sk,ak)。因为在系统状态sk中，姿态信息xk属于连续变量，而其它各项均为离散变量，它们之间不能直接混用。效用函数U(sk,ak)表示执行重构策略ak的代价，它关心的不是系统绝对姿态信息，而是姿态指向误差和能耗。通过式(6)计算一个决策周期内的控制误差和控制能耗，再代入式(5)计算重构代价。

定义最优性能指标J*(sk)为

(8)

根据Bellman最优性原理[18]，最优性能指标函数J*(sk)可以通过求解如下离散HJB方程获得

(9)

对应的最优重构策略π*(sk)为

(10)

2.2自适应动态规划方法

上述最优性能指标J*(sk)难以精确求解，本文使用ADHDP方法(也称Q-Learning方法[19])实现J*(sk)的近似求解。

首先，定义Q函数

Q(sk,ak)=U(sk,ak)+γJ*(sk+1)

(11)

该Q函数的含义为：从状态sk开始，首先执行动作ak，以后每步都遵循最优策略，得到性能指标函数的值。结合式(10)和式(11)，可以得到Q函数形式的最优重构策略

(12)

Q函数与最优性能指标J*之间存在着密切的联系。注意到

(13)

由式(11)和式(13)可得

(14)

式(14)是迭代法逼近Q函数的基础。

ADHDP结构如所图2所示，其主要包含三个部分：评价网络、执行网络和系统模型。评价网络用于近似Q函数，执行网络用于近似最优重构策略π*(sk)，系统模型用于对系统状态sk+1进行估计。

图2 ADHDP结构图Fig.2 The ADHDP structure

在图2中，执行网络的训练目标为最小化评价网络的输出Q(sk,ak)；评价网络的训练目标为最小化Q值近似误差Ed。Ed定义为

(15)

式中：

Ec(k)=U(sk,ak)+γQ(sk+1,ak+1)-Q(sk,ak)

(16)

ADHDP的策略迭代过程为：在故障情况下，系统状态为sk，通过采取重构策略执行动作ak，系统转移到状态sk+1。首先迭代更新评价网络的权值直至网络收敛；然后迭代更新执行网络的权值，使得评价网络输出Q(sk,ak)最小。当评价网络输出满足Ed<ζ(ζ为足够小的正常数)后，执行网络输出获得近似最优动作。

3 在轨重构算法

本节首先进行评价网络设计并给出其权值更新法则；然后针对执行网络进行简化设计；最后给出ADHDP的迭代训练算法实现在轨重构。

3.1评价网络与执行网络设计

1)评价网络

采用随机梯度下降法训练评价网络。输出层权值Wco(k)更新法则如下

(17)

(18)

定义隐藏层神经元j的误差项δj为

(19)

式中：δl为近似误差Ec(k)的第l项，n为输出层神经元个数。

隐藏层权值更新法则如下

Δwji=ηcδjxji

(20)

wji=wji+Δwji

(21)

式中：xji和wji分别为输入层神经元i到隐藏层神经元j的输入和权值。

2)执行网络

该简化设计避免了对执行网络的训练，因此仅需要训练评价网络，从而有效提高ADHDP的训练效率。

3.2改进的迭代学习算法

神经网络训练涉及大量的参数调整，容易陷入局部极值。当图2中的评价网络陷入局部极值，则会导致近似误差Ed(k)过大，决策模块无法获得最优重构策略。为此，本文参考文献[20]的方法，引入ε-greedy因子对神经网络进行训练。ε-greedy因子表示系统选择一个随机动作的概率。将ε从1退火到0。在迭代的初期，系统倾向选择随机动作，到了后期，系统倾向选用决策算法做出的决策。改进的迭代学习算法如下:

1) 使用随机权值初始化评价网络；

2) 初始化ε,d,N,V；

3) 令k=1,v=1；

4) 生成一个随机值r∈[0,1]，按照下式选择k时刻的动作ak

(22)

5) 按照式(5)计算效用函数U(sk,ak)；

6) 按照下式选择k+1时刻的动作ak+1并获得对应的Q(sk+1,ak+1)

(23)

7)按照式(17)～(21)更新评价网络权值直至网络收敛；

8)若ε>0，按照下式更新ε

(24)

9)令k←k+1。若k>N，则令k=1，v=v+1。若v>V，则结束训练；否则，返回步骤4。

4 仿真校验

本节将采用南京航空航天大学“TX-1”微小卫星[21]参数建立仿真模型，开展执行机构故障情况下的在轨重构算法验证。

4.1参数设置

卫星姿态控制系统配置了四个反作用飞轮，采用四斜装的安装方式，安装角ξ=45°，相对俯仰轴φ=54.74°，依次编号W1,W2,W3,W4，如图3所示。

图3 四斜装飞轮示意图Fig.3 The four wheels in a tetrahedral configuration

与之对应的故障因子Fk

(25)

可用配置方案集合A

A={A0,A1,A2,A3,A4}

(26)

配置方案描述见表1。

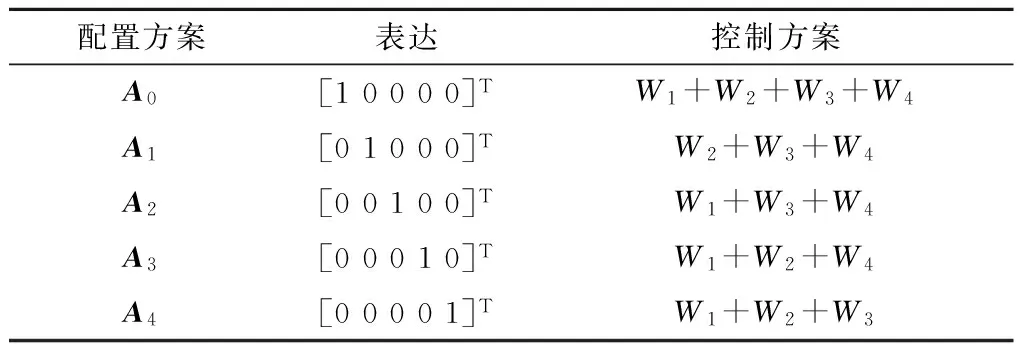
表1 配置方案描述Table 1 The description of reconfiguration policies

折扣因子γ和评价网络学习率ηc设置见表2。

表2 仿真参数设置Table 2 The simulation parameters

飞轮具有不同性能指标，故不同配置方案下指向精度有所差别。各配置方案指向精度见表3。

表3 指向精度Table 3 The control precisions

4.2结果分析

本节将通过4个案例来阐述所提出的在轨重构算法的有效性和合理性。4个案例的任务参数见表4。

表4 任务参数Table 4 The mission parameters

案例1.某任务时间窗口为H=[12,20)，即从t=12 min开始，到t=20 min结束；飞轮W2在t=9 min时发生30%的增益损失故障，即

(27)

图4和图5分别为在轨重构决策结果和评价网络输出曲线。在任意时刻，配置方案A0均具有更小的Q值。因此，在故障发生后，系统维持A0配置方案，无需进行重构。由于指向精度满足任务要求，可以继续执行任务。

图4 案例1在轨重构决策结果Fig.4 The on-orbit reconfiguration decision of case 1

图5 案例1评价网络输出曲线Fig.5 The critic network outputs of case 1

图6和图7的姿态曲线证实了图4所示决策结果的合理性。从图6可以看到，由于故障幅值较小，当前所用控制器足以克服故障影响，在t=12 min左右，系统姿态xk已经基本恢复稳定。若在此时采取重构，则其姿态曲线如图7所示，在t=12 min时姿态xk会出现明显振荡。此案例中故障发生时间距离任务窗口H只有3 min，重构过程的姿态振荡会影响任务的执行。因此，此时不进行重构是一个更合理的决策。

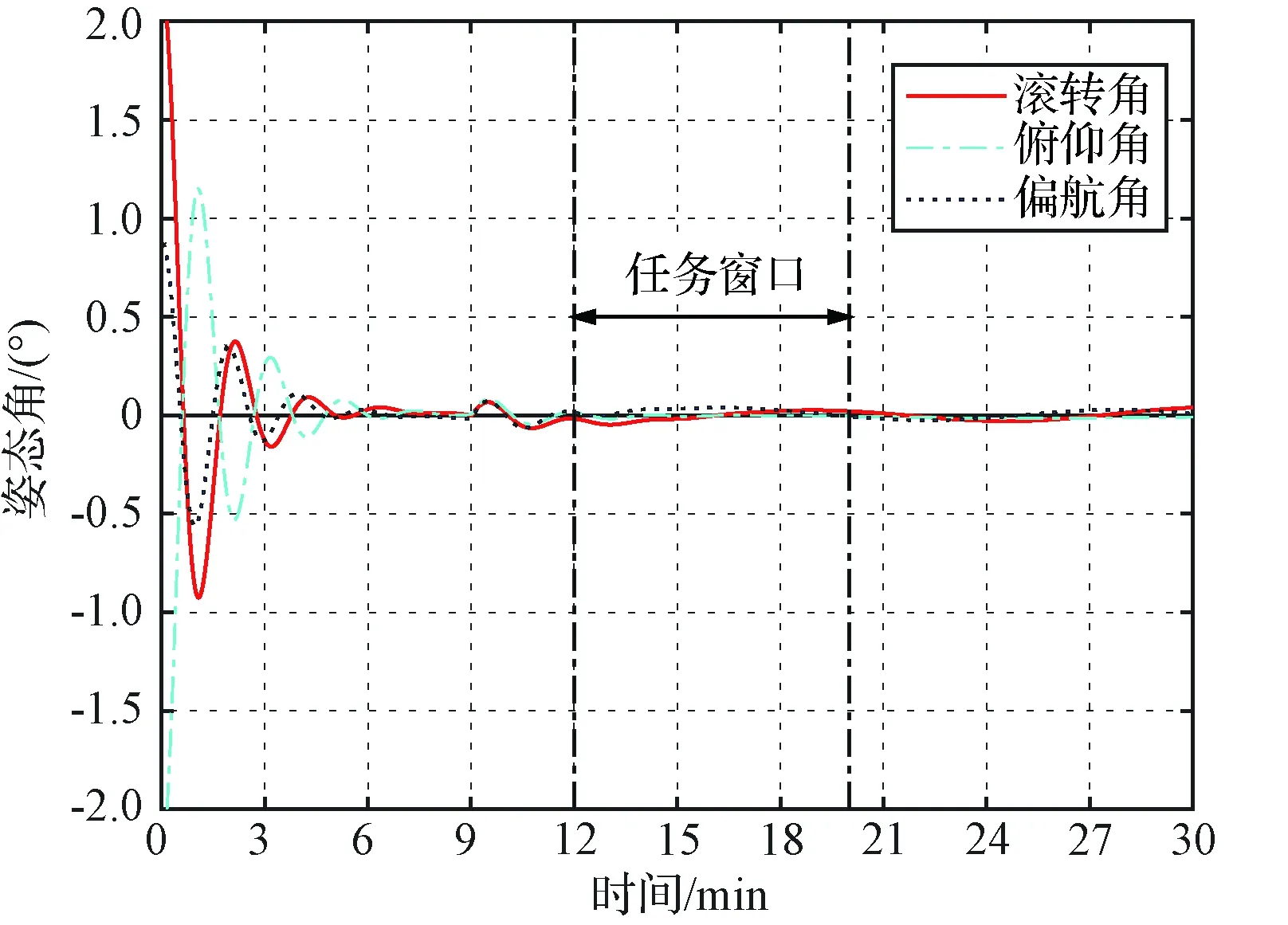
图6 故障后不实施重构系统姿态曲线Fig.6 The attitude curves without configuration

图7 故障后立即重构的姿态曲线Fig.7 The attitude curves with immediate reconfiguration

案例2.某任务时间窗口为H=[19,27)；飞轮W2在t=9 min时发生50%的增益损失故障，即

(28)

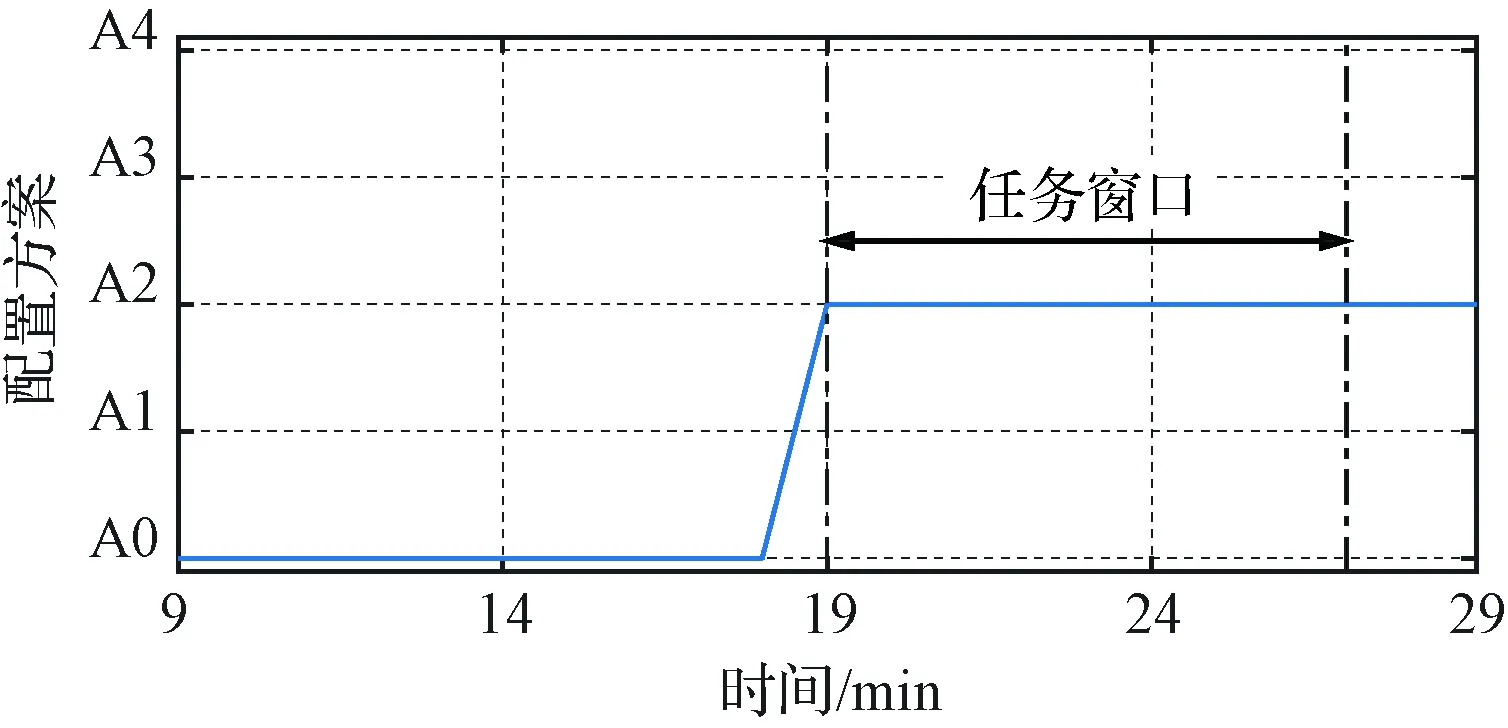
图8 案例2在轨重构决策结果Fig.8 The on-orbit reconfiguration decision of case 2

图9 案例2评价网络输出曲线Fig.9 The critic network outputs of case 2

案例3.某任务时间窗口为H=[19,27)；飞轮W2在t=9 min时发生50%的增益损失故障，故障描述如式(28)。

图10和图11分别为案例3的在轨重构决策结果和评价网络输出曲线。在此案例中，系统可以通过重构切换至配置方案A0，使得指向精度满足任务要求。但是，由于任务能耗需求大，而任务优先级低，若进行系统重构，会带来较大能耗上的代价。从图11可以看到，在满足任务约束时，配置方案A0具有更小的Q值，不进行系统重构。故障发生后，若不进行重构，则指向精度已不能满足任务要求，故任务取消，系统进入安全模式。

图10 案例3在轨重构决策结果Fig.10 The on-orbit reconfiguration decision of case 3

图11 案例3评价网络输出曲线Fig.11 The critic network outputs of case 3

案例4.某任务时间窗口为H=[19,27)；飞轮W2在t=9 min时发生50%的增益损失故障，故障描述如式(28)。

图12和图13分别为案例4系统在轨重构决策结果和评价网络输出曲线。在提高任务优先级约束之后，面对更加重要的任务，虽然系统重构仍然会带来较大的能耗代价，但配置方案A2具有更小的Q值，系统为完成重要任务，不惜消耗较大的能量进行系统重构。

图12 案例4在轨重构决策结果Fig.12 The on-orbit reconfiguration decision of case 4

图13 案例4评价网络输出曲线Fig.13 The critic network outputs of case 4

由以上仿真分析结果可知，本文提出的在轨重构算法能够综合考虑任务的精度约束、能耗约束和任务优先级约束，根据故障诊断信息，做出合理的在轨重构决策。面对幅值较小的故障，为避免系统重构导致的姿态振荡影响任务执行，系统不进行重构，继续完成任务；面对幅值较大的故障，系统通过重构切换至合适的配置方案，以恢复姿态指向精度，满足任务需求。面对优先级较低的任务，系统为减少能源消耗，合理地取消原定任务；面对优先级较高的任务，系统又不惜付出较大的能耗代价来完成任务。

5 结 论

本文针对任务约束下的航天器姿态控制系统在轨重构问题，提出了一种基于自适应动态规划的在轨重构优化决策算法，并且基于南京航空航天大学“TX-1”微小卫星仿真模型对所提方法进行仿真验证。仿真结果表明，本文所提出的在轨重构算法，能够在保障航天器安全性不受威胁的前提下，尽可能满足任务约束，完成原定任务，从而最大化利用航天器平台资源。在工程实际中，系统重构除了要考虑任务约束外，还需要考虑重构时间等约束，后续我们将针对此类课题开展进一步研究。

[1] Cheng Y H, Jiang B, Fu Y, et al. Robust observer based reliable control for satellite attitude control systems with sensor faults[J]. International Journal of Innovative Computing, Information and Control, 2011, 7(7): 4149-4160.

[2] 姜斌, 冒泽慧, 杨浩, 等. 控制系统的故障诊断与故障调节[M]. 北京: 国防工业出版社, 2009.

[3] 姜连祥, 李华旺, 杨根庆, 等. 航天器自主故障诊断技术研究进展[J]. 宇航学报, 2009, 30(4): 1320-1326. [Jiang Lian-xiang, Li Hua-wang, Yang Gen-qing, et al. A survey of spacecraft autonomous fault diagnosis research[J]. Journal of Astronautics, 2009, 30(4): 1320-1326.]

[4] 邢琰, 吴宏鑫, 王晓磊, 等. 航天器故障诊断与容错控制技术综述[J]. 宇航学报, 2003, 24(3): 221-226. [Xing Yan, Wu Hong-xin, Wang Xiao-lei, et al. Survey of fault diagnosis and fault-tolerance control technology for spacecraft[J]. Journal of Astronautics, 2003, 24(3): 221-226.]

[5] 胡宇桑, 王大轶, 刘成瑞. 卫星姿控系统可重构性综合评价方法研究[J]. 宇航学报, 2015, 36(5): 549-556. [Hu Yu-sang, Wang Da-yi, Liu Cheng-rui. Reconfigurability comprehensive evaluation for satellite attitude control system[J]. Journal of Astronautics, 2015, 36(5): 549-556.]

[6] Tudoroiu N, Khorasani K. Fault detection and diagnosis for satellite’s attitude control system (ACS) using an interactive multiple model (IMM) approach[C]. Proceedings of 2005 IEEE Conference on Control Applications, Toronto, Canada, August 28-31,2005.

[7] 陈雪芹, 张迎春, 耿云海, 等. 基于IMM/EA的卫星姿态控制系统重构容错控制[J]. 系统工程与电子技术, 2007, 29(5): 774-777. [Chen Xue-qin, Zhang Ying-chun, Geng Yun-hai, et al. IMM/EA-based on-orbit reconfigurable fault-tolerant control for satellite attitude control system[J]. Systems Engineering and Electronics, 2007, 29(5): 774-777.]

[8] Talebi H, Patel R. An intelligent fault detection and recovery scheme for reaction wheel actuator of satellite attitude control systems[C]. IEEE International Symposium on Intelligent Control, Munich, Germany, October 4-6,2006.

[9] 樊雯, 程月华, 姜斌, 等. 卫星姿态控制系统的可重构性分析[J]. 宇航学报, 2014, 35(2): 185-191. [Fan Wen, Cheng Yue-hua, Jiang Bin, et al. Reconfigurability analysis for satellite attitude control systems[J]. Journal of Astronautics, 2014, 35(2): 185-191.]

[10] Nasir A, Atkins E, Kolmanovsky I. A mission based fault reconfiguration framework for spacecraft applications[C]. Infotech @Aerospace 2012, Garden Grove, America, June 19-21,2012.

[11] 王晓晖, 李爽. 深空探测器约束简化与任务规划方法研究[J]. 宇航学报, 2016, 37(7): 768-774. [Wang Xiao-hui, Li Shuang. Research on constraint simplification and mission planning method for deep space explorer[J]. Journal of Astronautics, 2016, 37(7): 768-774.]

[12] 赵凡宇, 徐瑞, 崔平远. 启发式深空探测器任务规划方法[J]. 宇航学报, 2015, 36(5): 496-503. [Zhao Fan-yu, Xu Rui, Cui Ping-yuan. Heuristic mission planning approach for deep space explorer[J]. Journal of Astronautics, 2015, 36(5): 496-503.]

[13] Werbos P J. Advanced forecasting methods for global crisis warning and models of intelligence[J]. General Systems Yearbook, 1977, 22(12): 25-38.

[14] 刘德荣, 李宏亮, 王鼎. 基于数据的自学习优化控制: 研究进展与展望[J]. 自动化学报, 2013, 39(11): 1858-1870. [Liu De-rong, Li Hong-liang, Wang Ding. Data-based self-learning optimal control: research progress and prospects[J]. Acta Automatica Sinica, 2013, 39(11): 1858-1870.]

[15] 赵冬斌, 刘德荣, 易建强. 基于自适应动态规划的城市交通信号优化控制方法综述[J]. 自动化学报, 2009, 35(6): 676-681. [Zhao Dong-bin, Liu De-rong, Yi Jian-qiang. An overview on the adaptive dynamic programming based urban city traffic signal optimal control[J]. Acta Automatica Sinica, 2009, 35(6): 676-681.]

[16] Boaro M, Fuselli D, De Angelis F, et al. Adaptive dynamic programming algorithm for renewable energy scheduling and battery management[J]. Cognitive Computation, 2013, 5(2): 264-277.

[17] Fuselli D, De Angelis F, Boaro M, et al. Action dependent heuristic dynamic programming for home energy resource scheduling[J]. International Journal of Electrical Power & Energy Systems, 2013, 48: 148-160.

[18] Bellman R E, Dreyfus S E. Applied dynamic programming[M].Princeton: Princeton University Press, 2015.

[19] Wang F Y, Zhang H G, Liu D R. Adaptive dynamic programming: an introduction[J]. IEEE Computational Intelligence Magazine, 2009, 4(2): 39-47.

[20] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature,2015,518(7540):529-533.

[21] 刘海颖. 微小卫星姿态控制系统关键技术研究[D]. 南京: 南京航空航天大学, 2008. [Liu Hai-ying. Research on attitude control system key technologies for micro-satellite[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.]

Mission-ConstrainedSpacecraftAttitudeControlSystemOn-OrbitReconfigurationAlgorithm

CHEN Jia-wen1, CHENG Yue-hua2,3, JIANG Bin1, LU Ning-yun1, YANG Tian-she4

(1. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China；2.College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;3. Department of Mechanical Engineering，York University, Toronto M3J 1P3, Canada;4. Key Laboratory of Spacecraft In-Orbit Fault Diagnosis and Maintenance, Xi’an 710043, China)

An on-orbit reconfiguration algorithm based on adaptive dynamic programming (ADP) is proposed to reconfigurate the controller of a spacecraft attitude control system (ACS) in case of fault with the consideration of the ongoing missions. Firstly, a utility function and a performance index function regarding the scheduled spacecraft mission are designed, and the optimal reconfiguration policy is obtained as a solution of the Hamilton-Jacobian-Bellman(HJB) equation. Secondly, the action-dependent heuristic dynamic programming (ADHDP) approach is used to approximately solve the HJB equation, avoiding the curse of the dimensionality of directly solving HJB. Finally, simplifying the design of the ADHDP action network is conducted to make the iterative training process faster, and theε-greedy factor is introduced in the training process to avoid getting in local minimum too early. Simulation results show the effectiveness of the proposed method.

Attitude control system (ACS); On-orbit reconfiguration; Mission constraints; Adaptive dynamic programming (ADP)

V448

A

1000-1328(2017)09- 0989- 09

10.3873/j.issn.1000-1328.2017.09.012

2017- 04- 21;

2017- 06- 27

国家自然科学基金(61673206,61622304)；中央高校基本科研业务费专项资金(2016083)；南京航空航天大学研究生创新基地(实验室)开放基金(kfjj20160315)

陈嘉文(1993-)，男，硕士，主要从事航天器姿态控制系统故障诊断与容错控制研究。

通信地址：江苏省南京市将军大道29号(211106)

电话：(025)84892305-6041

E-mail: ivancjw.xy@gmail.com

姜斌(1966-)，男，博士，教授，主要从事复杂系统的故障诊断与容错控制研究。本文通信作者。

通信地址：江苏省南京市将军大道29号(211106)

电话：(025)84892305-6041

E-mail: binjiang@nuaa.edu.cn