基于立体视觉Tri-EKF算法的空间非合作目标运动与结构估计

王 珂，于占海，刘 宏，李瑞峰，郭本生

(哈尔滨工业大学机器人研究所，哈尔滨150080)

基于立体视觉Tri-EKF算法的空间非合作目标运动与结构估计

王 珂，于占海，刘 宏，李瑞峰，郭本生

(哈尔滨工业大学机器人研究所，哈尔滨150080)

针对空间非合作目标的运动状态及外形结构估计的双重扩展卡尔曼滤波(Dual EKF)算法存在运动状态变量耦合及收敛速度慢的问题。基于立体视觉观测模型，引入特征线作为新观测量分析了目标平移与旋转运动估计的解耦性，提出三重扩展卡尔曼滤波(Tri-EKF)算法，实现了对目标旋转、平移运动以及结构参数的串行估计。本文对两种算法进行仿真比较，通过试验校验Tri-EKF算法。结果表明：有限次观测下，Tri-EKF算法对目标运动估计收敛速度更快，平均估计误差更小。

非合作目标；Tri-EKF算法；运动及结构估计；立体视觉

0 引 言

空间航天器在故障、失效或完成任务后都可能在空间内自由漂浮成为太空垃圾[1]。这些不提供有效合作信息的空间非合作目标占用空间轨道资源，给正常运行的航天器造成极大威胁。而具备太空垃圾清除能力的空间机器人是捕获和回收非合作目标的有效手段。机器人对非合作目标自主操作，要求其有能力评估目标运动姿态和结构外形。因此，实现目标位置姿态及目标三维结构外形的估计，对机器人可靠作业具有重要意义。

针对非合作目标运动和结构估计，Terui等[2]采用迭代最近点(Iterative closest point, ICP)算法将测量数据与3D模型进行匹配得到目标相对姿态的估计结果，但该方法需要先验模型并且无法实时估计。斯坦福大学的Augenstein等[3]提出了基于粒子滤波的快速即时定位与地图构建(Fast simultaneous localization and mapping,Fast SLAM)递归估计6自由度姿态估计算法，该方法不需要目标先验知识，但粒子滤波计算量大，实时性较差。Segal等[4]采用扩展卡尔曼(Extended Kalman filter,EKF)估计目标运动状态和结构参数，其集中估计方式的状态向量会不断增广，可能产生 “维度灾难”问题。国内学者，蔡晗等[5]利用目标的几何特征，通过双目视觉测量算法解算出目标相对姿态信息，但该方法对目标几何特征要求较高，目标形状需是矩形。周军等[6]提出基于陀螺仪、扩展卡尔曼和加速度计的非合作目标的位姿估计方法，该方法鲁棒性较好，但收敛速度较慢。翟光等[7]在传统卡尔曼算法基础上提出了一种姿态指向跟瞄导航算法，避免了传统扩展卡尔曼算法近似线性化过程中的大量矩阵求导运算，因而提高了跟踪导航滤波的收敛速度。郝刚涛等[8]提出一种基于EKF的单目视觉图像序列的非合作目标相对姿态估计方法，该方法会引起“维度灾难”问题，同样降低收敛速度。上述方法多以联合扩展卡尔曼滤波(Joint EKF)[9]为基础，因此会引入增广状态向量。Ljung[10]指出，增广状态向量会引入运动状态和结构参数间的耦合。Liu等[11]还证明，若增广状态向量维数为n+m(n为运动状态参数维数，m为结构特征点数量)，Joint EKF将出现n+m维矩阵的三次相乘，会因状态向量未知量较多而使滤波估计不稳定乃至发散，造成数值病态问题并限制结构点数量。因此，Zhang等[12]提出双重扩展卡尔曼滤波(Dual EKF)，将运动状态参数和结构点估计进行串行分离，以解决两者耦合关系。Zhang[13]针对串/并行Dual EKF，证明了串行Dual EKF为无偏估计。虽然系统状态维数降低，但目标平移及旋转运动仍要同时估计。

本文针对空间机器人超近距离非合作目标外结构与运动参数在线估计，通过双目立体视觉观测和跟踪动态目标的图像特征。主要贡献在于建立了以特征线结构点为观测特征的观测模型，提出三重扩展卡尔曼滤波(Tri-EKF)算法对目标平移状态分量、旋转状态分量，以及表面三维结构点进行串行估计。相对于Dual EKF，Tri-EKF进一步降低系统状态向量维数，保持实时计算特性，并提高了运动参数的估计速度，同时实现了目标三维外形结构点的在线估计。本文通过仿真试验综合比较Dual EKF和Tri-EKF算法的收敛速度，收敛精度等，并基于试验平台校验Tri-EKF算法在目标特性估计和三维点云重构估计的有效性。

1 非合作目标运动及观测模型

自由悬浮状态的空间非合作目标具有平动、绕自旋轴旋转的运动特性，首先建立坐标系，运动模型，结构模型以及观测模型。

1.1坐标系定义

建立如图1所示的三个坐标系，分别为：

视觉坐标系OC，为立体视觉观测系统测量目标表面特征点的基准坐标系。

结构坐标系OS，位于刚体目标表面并随目标运动，结构特征点在该坐标系下坐标不随时间变化。

目标坐标系OT, 目标结构未知及旋转中心未知，旋转中心在OS中位置作为估计参量。

OS与OT的坐标轴平行，定义d=[dx,dy,dz]T为目标坐标系OT相对于视觉坐标系OC的位移矢量。目标围绕过OT的自旋轴旋转。

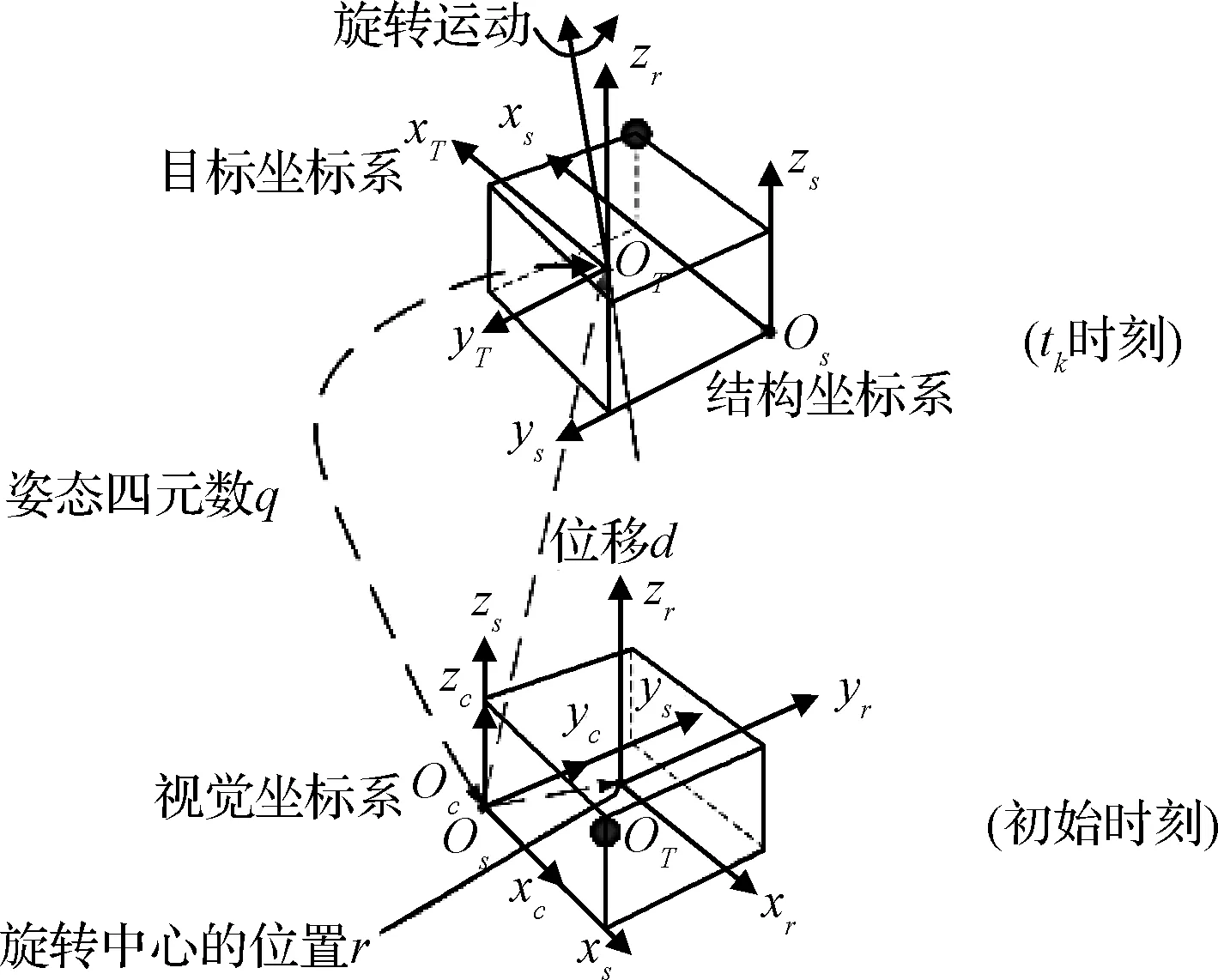
图1 坐标系Fig.1 Coordinate system

1.2运动模型

目标运动包括自旋转动及OT相对于OC平动，表述为位移、速度、旋转中心位置、姿态角和角速度为参数的目标运动状态模型。

1.2.1 平移运动

设OT相对于OC的速度矢量为v=[vx,vy,vz]T,矢量r=[rx,ry,rz]T为自旋中心OT在OS的位置，将其归结为平移运动参数，因此目标离散时间方程为

(1)

式中：tk-1、tk代表k-1和k两个连续离散采样时刻，τ表示采样时间间隔,ξk表示加速度项。

1.2.2 旋转运动

采用四元数q=[q0,q1,q2,q3]T描述目标与OC的相对旋转姿态[14]。设其相对OC的角速度矢量为ω=[ωx,ωy,ωz]T，建立目标姿态四元数与旋转角速度间的离散表达式为

(2)

式中：Φ(ωk-1)为关于ωk-1的4阶矩阵[15]。

1.2.3 运动学方程

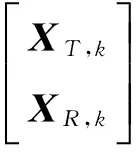
(3)

式中：FT和FR分别代表平移和旋转状态分量的状态转移矩阵，平移分量为XT=[dT,vT,rT]T，旋转分量为XR=[qT,ωT]T，wk为高斯白噪声。

1.3结构模型

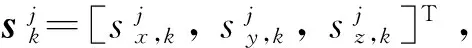
XS,k=XS,k-1

(4)

1.4立体视觉观测模型

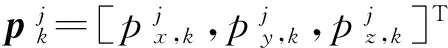
(5)

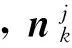
设tk时刻目标表面有m特征点被同时观测，定义三维坐标向量Zk，则观测量pk的三维结构坐标参数与目标运动参量间的变换关系

(6)

由此，可以得到目标观测量Zk与运动参数XM,k和结构参数XS,k间的观测方程

(7)

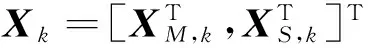
2 Tri-EKF目标运动与结构估计

Tri-EKF在Dual EKF结构及运动参数解耦基础上，将特征线作为旋转运动观测量，实现目标旋转与平移运动参数的解耦。

2.1特征线

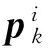
(8)

两式相减得

(9)

式(9)不含平移变量，整理得

(10)

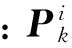
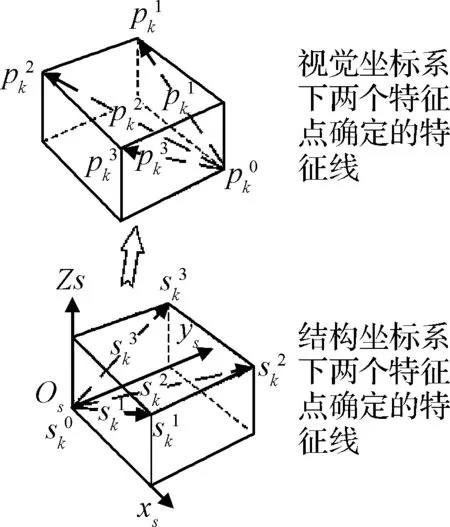
图2 OC坐标系与OS坐标系下的特征线Fig.2 The feature line under OC and OS coordinate

式(10)定义的新观测量建立了目标特征线与旋转向量q间的函数关系，不需要平移运动估计结果，仅通过特征线观测量便可实现对目标旋转运动的独立估计。

基于tk时刻m条特征线，建立目标观测方程

(11)

2.2Tri-EKF算法

图3为Tri-EKF结构框图，以目标特征线为观测量，采用旋转运动估计器、平移运动估计器和结构参数估计器对目标参数进行串行估计，从而实现状态向量降维。

旋转运动估计器先通过特征点构造特征线，然后将特征线组成的向量ZR,k作为观测量；平移运动估计器和结构参数估计器分别使用特征点三维坐标所组成的向量ZT,k和ZS,k作为观测量，随着各估计器间估计结果的传递，观测方程中未知量个数逐渐减少。

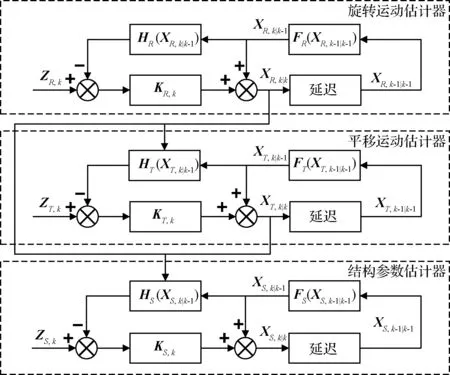
图3 Tri-EKF结构框图Fig.3 Structure diagram of Tri-EKF

旋转运动估计状态向量为XR，向量元素为四元数q和角速度ω，状态方程为

(12)

式(11)为旋转运动估计器观测方程，为特征线组成的向量ZR,k。

平移运动估计器状态向量为XT，向量元素为平移量d，平移速度v和r，状态方程为

(13)

旋转估计结果XR,k|k在该阶段为已知量，因此将其作为输入量会使平移估计器观测方程未知量个数减少，其观测方程为

ZT,k=HTXT,k|k-1+nk=

(14)

式中：HT为关于平移状态变量XT,k|k-1的观测雅可比矩阵。

目标结构参数估计器状态向量为XS，状态方程与Dual EKF结构参数估计器相同，即：

(15)

旋转和平移估计结果XR,k|k、XT,k|k作为已知量输入到结构参数估计器观测方程中，因此观测方程未知量个数在平移估计器的基础上再次减少，其观测方程为

ZS,k=HSXS,k|k-1+nk=

(16)

式中：HS为关于结构状态变量XS的观测雅可比矩阵。

Tri-EKF按顺序依次估计旋转参数、平移参数以及结构参数，前面滤波器的结果将作为后面滤波器观测方程的输入，由于估计结果为已知量，因此会减少后面滤波器观测方程的未知量个数。Tri-EKF算法主要步骤如下：

1)旋转、平移和结构滤波器的时间更新

(17)

式中：Xk-1|k-1为tk时刻滤波估计值，Xk|k-1为tk时刻滤波预测值，FS为结构状态分量的状态转移矩阵。

2)旋转运动估计器的观测更新

XR,k|k=XR,k|k-1+KR,k(ZR,k-HRXR,k|k-1)

(18)

式中：Xk|k为tk时刻滤波估计值，Kk为卡尔曼增益，HR为关于旋转状态变量XR,k|k-1的观测雅可比矩阵。

3)平移运动估计器观测更新

XT,k|k=XT,k|k-1+

(19)

4)结构参数估计器观测更新

XS,k|k=XS,k|k-1+

(20)

3 仿真

3.1仿真试验1

图4所示运动目标为底半径5 m，高10 m圆柱体，圆柱体上、中、下圆面对称分布4个点，共12个特征点。仿真假设特征点已经提取并正确匹配。

目标初始位置设在相机坐标系(50, 50, 50) m处，运动形式为平移和旋转复合运动。目标沿相机坐标系X、Y、Z轴的平移速度均为0.1 m/s，同时以π/50 (rad·s-1)的角速度绕过体心的方向向量(1, 1, 1)进行旋转。选择圆柱体上表面圆周上一点为结构坐标系原点，建立结构坐标系OS。计算目标特征点在相机坐标系下理论坐标值并引入高斯白噪声，将含有噪声的特征点三维坐标作为算法实际观测值。

图4 仿真圆柱体模型Fig.4 Simulation cylinder model

各状态向量初始值设定如表1所示。滤波开始阶段将状态协方差矩阵初始值P0设置较大。本仿真将方阵P0的对角元设为1，观测噪声协方差矩阵Sk对角元设为0.25，根据滤波器结构分别设置协方差矩阵维数。

表1 仿真试验1的状态向量初值Table 1 The initial value of the state vector in the first simulation experiment

为了校验Tri-EKF算法的有效性，定义状态变量估计误差并对Tri-EKF和Dual EKF两种算法的估计结果进行定量比较：

1)位移误差：

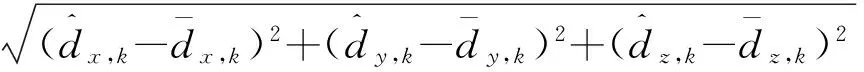
2)速度误差：

3)旋转中心位置误差：

4)角速度误差：

式中：上标“^”表示tk时刻状态变量滤波估计值，上标“-”表示tk时刻状态变量真实值。

图5为平移运动估计曲线。Tri-EKF对目标平移运动估计的收敛速度比Dual EKF快，Tri-EKF在50帧左右即可收敛，而Dual EKF至少需100帧。

图6为角速度估计曲线。角速度估计收敛速度相比于平移都有所提高。Tri-EKF收敛速度仍然比Dual EKF快，Tri-EKF在40帧左右即可收敛，Dual EKF在70帧左右收敛。

图7为估计误差，收敛后估计误差基本一致，但Tri-EKF收敛速度快，估计误差下降快，在有限次(无论是否稳定)观测下Tri-EKF的平均估计误差更小。

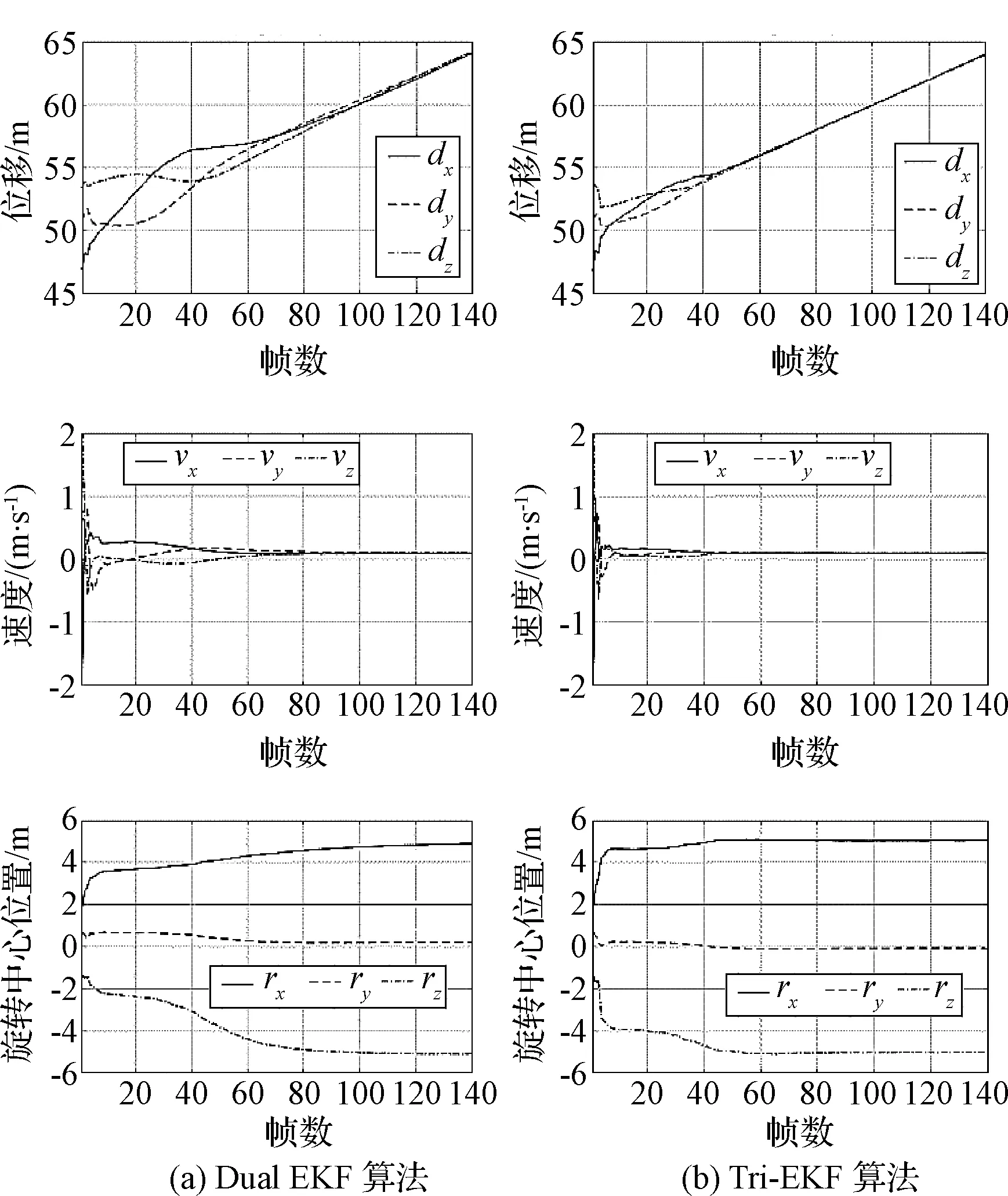
图5 平移运动估计曲线Fig.5 Estimation of translation motion

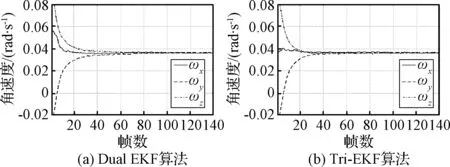
图6 角速度估计曲线Fig.6 Estimation of angular velocity

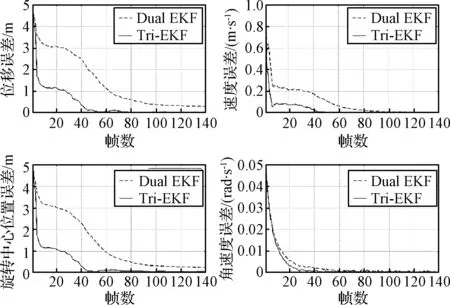
图7 估计误差曲线Fig.7 Estimation error

3.2仿真试验2

运动目标为棱长10 m的正方体，如图8所示，同样假设仿真过程中特征点已经提取并正确匹配。目标初始位置设在相机坐标系(50, 50, 50) m处，运动形式为平移和旋转的复合运动。目标沿相机坐标系X、Y、Z轴的平移速度均为0.1 m/s，同时以π/50(rad/s)的角速度分别绕相机坐标系的Z、X、Y旋转。在正方体上表面某一顶点处建立结构坐标系OS。同样将含有高斯噪声的特征点三维坐标作为算法观测值。

图8 仿真正方体模型Fig.8 Simulation cube model

ωk真实初值为(0.063, 0.063, 0.063)，本次仿真试验仍设定算法初值为(0.0, 0.0, 0.0)，其他参数与仿真试验1相同。状态协方差矩阵P0是对角元为3的方阵，观测噪声协方差矩阵Sk是对角元为0.5的方阵。

平移运动估计结果如图9所示，分析曲线可知，Tri-EKF在50帧左右收敛，Dual EKF在100帧左右收敛，说明Tri-EKF比 Dual EKF具有更快的平移估计收敛速度。

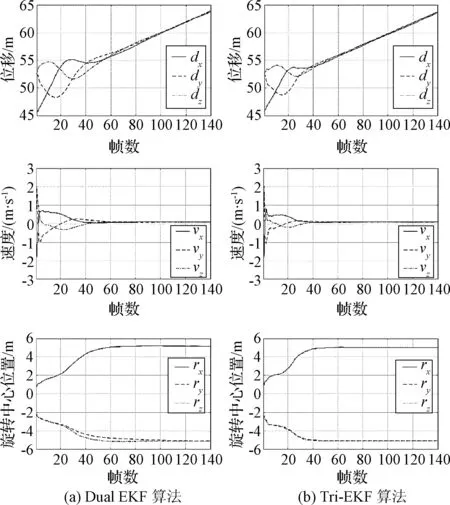
图9 平移运动估计结果Fig.9 Estimation of translation motion

图10为角速度估计曲线。Tri-EKF的收敛速度比Dual EKF快10帧左右，大约在50帧左右收敛，后者收敛至少需要60帧。算法旋转估计收敛速度比各自的平移估计收敛速度快。

图11为估计误差，相比于Dual EKF前50帧，Tri-EKF误差降低迅速，算法收敛后估计误差基本一致，但Tri-EKF收敛速度快，估计误差下降快，因此在有限次(无论是否稳定)观测下Tri-EKF平均估计误差更小。

图10 角速度估计曲线Fig.10 Estimation of angular velocity

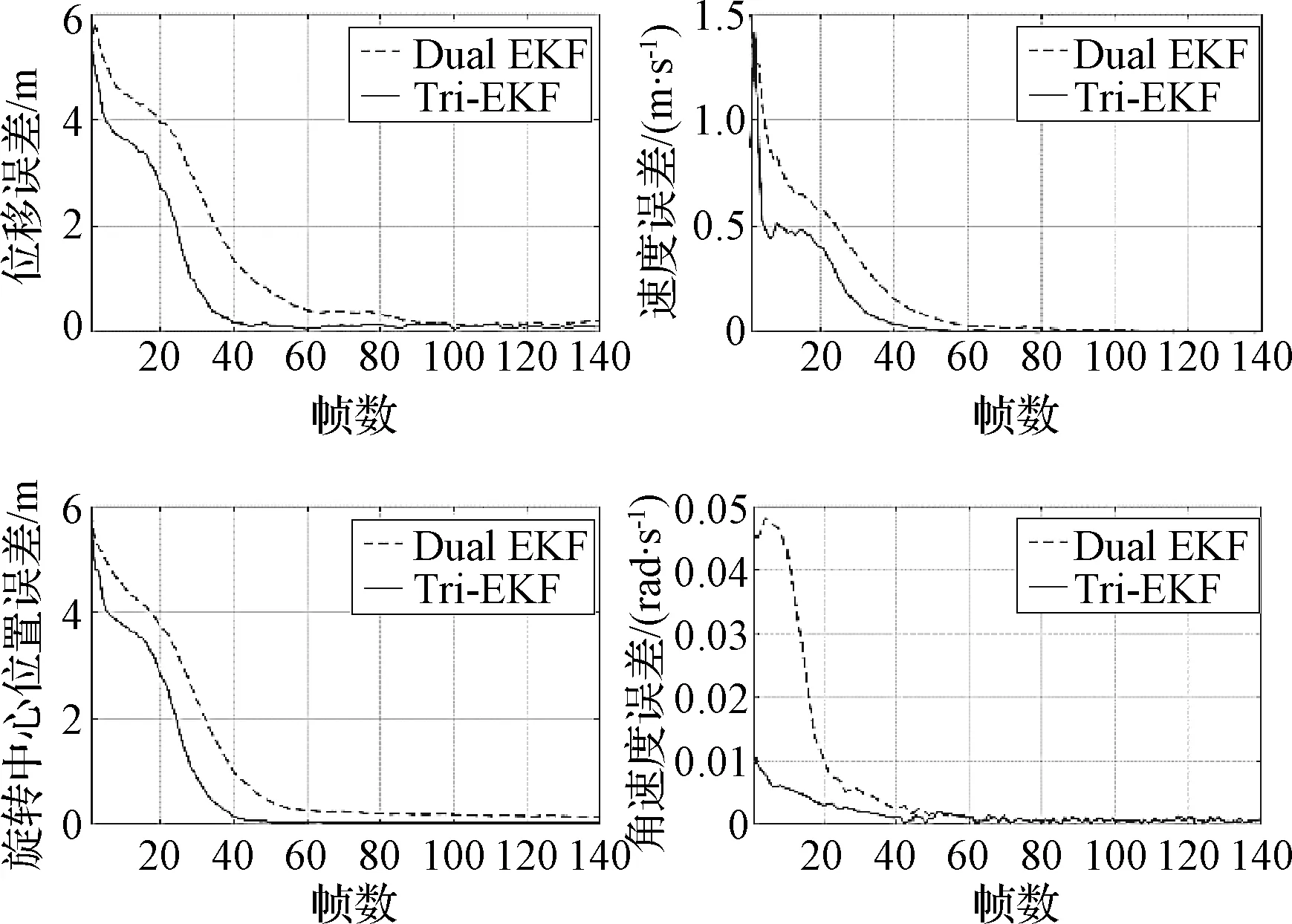
图11 估计误差Fig.11 Estimation error

3.3结果分析

综合分析以上两个仿真试验的估计结果可以得出以下结论：相比于Dual EKF算法，Tri-EKF算法优势主要体现在有限次平均估计误差和收敛速度上。Tri-EKF对旋转、平移、结构参数分别估计，降低了系统状态向量维数，当Tri-EKF旋转估计收敛并开始进行平移估计时，Dual EKF仍在进行旋转参数估计。旋转估计收敛速度要快于平移估计收敛速度，因此Tri-EKF收敛速度快的优势在平移运动中体现得更加明显。由于收敛速度快，使得Tri-EKF在有限次观测情况下的平均估计误差更小。

虽然Dual EKF实现了运动参数和结构参数的解耦，但其运动参数间存在耦合，导致收敛速度慢，Tri-EKF实现了旋转和平移参数的解耦，因此加速了各运动分量的估计速度。

Tri-EKF适应多种形式参数模型，由于基于EKF架构采用串行估计策略，运动状态向量维数不同，收敛速度有差异，但线性化过程相同，因此和Dual EKF收敛后的运动估计精度接近。

4 试验

4.1试验平台

图12所示试验平台主要由三部分组成，计算机处理系统所用CPU为酷睿i5- 4690 K，主频3.50 GHz；立体视觉系统采用Bumblebee2相机，分辨率设为640×480；两自由度运动平台与计算机间通讯方式为RS 485，并通过PMC-20MT-3三轴控制器控制K101DX60J电动旋转台和DTX1205- 600直线丝杠导轨来模拟目标的两种运动形式。所用目标模型为高20.5 cm，宽30 cm的“神舟九号”模型。采用ORB算法[17]提取左右图像特征点，然后通过PyrLK[18]算法跟踪前后两帧左右图像特征点，并筛选跟踪结果得到新时刻左右图像的特征匹配对。设置特征匹配对数量阈值，当匹配对数量小于阈值时则认为特征点对信息过少不足以实现对目标运动和结构参数的估计，需要对当前图像重新进行特征提取及匹配以补充新匹配对；若大于阈值，则用视差法计算特征点三维坐标，并作为Tri-EKF算法观测量用于目标运动状态和结构参数的递推估计。

图12 试验平台Fig.12 Experimental platform

4.2目标运动估计

4.2.1 平移运动

设定目标在相机坐标系x轴方向和z轴方向平移速度分别为9.7 mm/s和6.8 mm/s。试验得到的目标平移运动估计曲线与误差曲线如图13所示(仅绘制x轴和z轴方向估计数据)。

图13 平移运动估计结果Fig.13 Estimation results of translation motion

对于纯平移运动，Tri-EKF算法在10帧左右即可收敛，说明算法能够实现对纯平移运动的较快估计。10帧到150帧时估计结果相对稳定，这是因为在该阶段内目标与相机间距离较近，特征点测量精度较高，使得位移估计与速度估计误差较稳定。帧数为150到200帧时，随着目标与相机间距离的增大，测量噪声增大，位移估计与速度估计误差有小幅上扬趋势。将稳定阶段的平均误差作为算法估计精度的衡量标准，Tri-EKF算法在x轴和z轴方向上的速度估计平均误差分别为0.41 mm/s和0.31 mm/s，位移估计平均误差分别为6.24 mm和4.58 mm，估计误差较小，精度较高。

4.2.2 旋转运动

设定电动转台转动(相机y轴)速度为20°/s，将直线滑台移动速度设为零。试验得到目标旋转运动估计曲线与误差曲线(见图14)。图14(a)为四元数估计曲线，对应的欧拉角如图14(b)所示，其中偏航角，俯仰角和滚转角平均误差分别为3.07°,1.43°和1.40°。偏航角(取值范围(-180°,180°))在±180°处存在切换跳变现象。图14(c)为欧拉角误差曲线，偏航角估计误差平均在5°内，当角度为±180°时会产生较大误差，但最大误差不超过10°。这是因为通过四元数对欧拉角进行反三角函数求解时在±180°位置处存在奇异。试验中俯仰角和滚转角估计曲线在零值附近以±3°幅度振荡，这是因为相机y轴与旋转台轴线难以保证完全平行。图14(d)为目标角速度估计曲线，估计结果平均0.356 rad/s，与理论值0.349 rad/s相差0.007 rad/s，误差较小，并且曲线在20帧左右即可收敛，具有较快的估计速度。

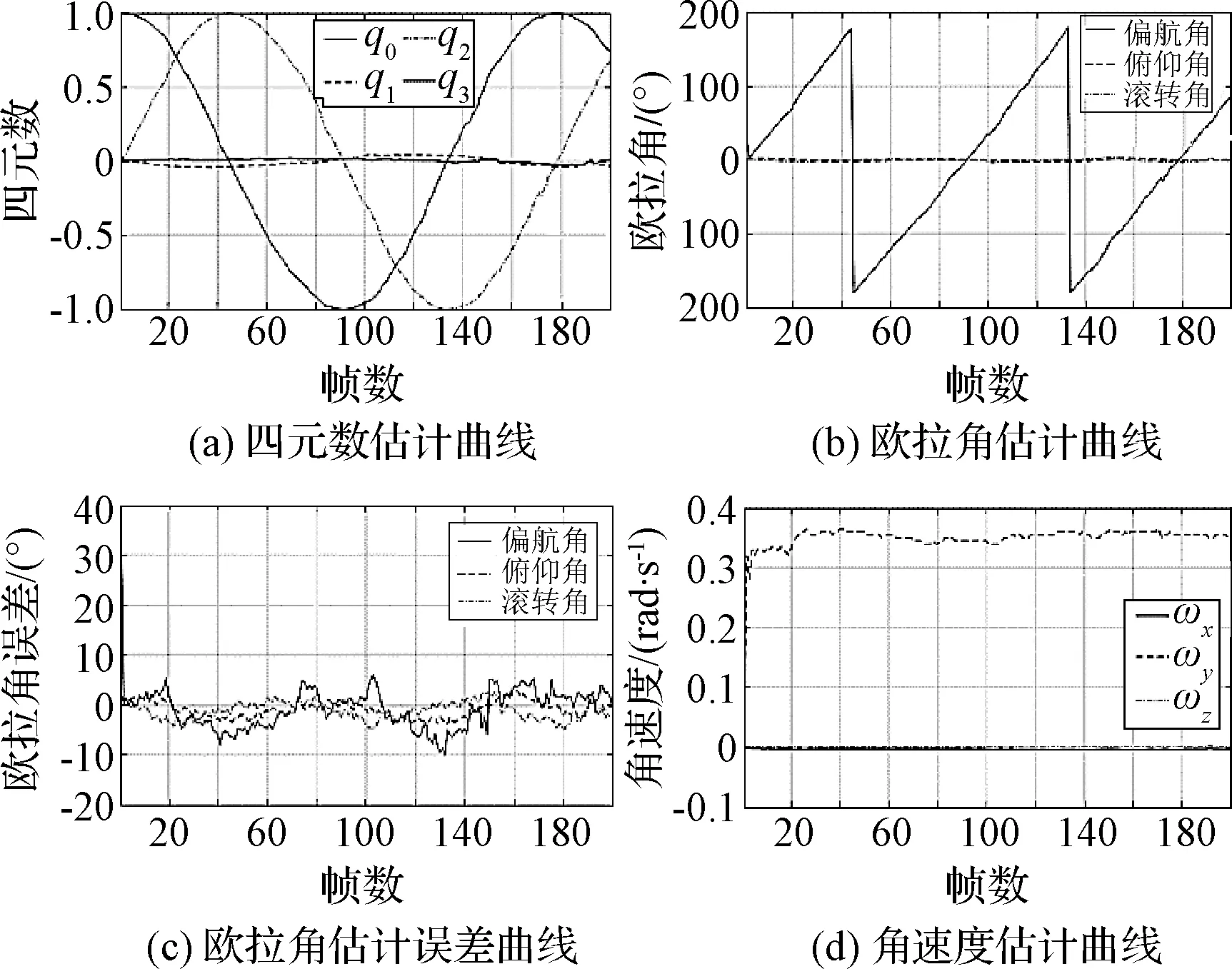
图14 旋转运动估计结果Fig.14 Estimation results of rotational motion

4.2.3 复合运动

设定目标在相机坐标系x轴方向和z轴方向平移速度分别为8 mm/s和6 mm/s，电动转台转动速度为20 °/s(0.349 rad/s)。试验得到的目标运动估计曲线与误差曲线如图15所示。开始时算法估计误差较大，曲线不平稳，随着不断迭代，约在50帧左右收敛。由收敛后曲线可知，z轴和x轴方向位移估计平均误差分别为5.9 mm和7.6 mm，平移速度平均估计误差为0.77 mm/s和0.14 mm/s，偏航角、俯仰角和滚转角平均估计误差分别为7.43°、4.62°和5.17°。角速度估计平均值为0.367 rad/s，误差为0.018 rad/s。相比于纯平移和纯旋转运动，复合运动具有更加复杂的形式，因此在对运动参数进行估计时，算法的收敛速度有所降低，误差也有所增大，但整体而言算法仍然能够得到较好的估计结果。

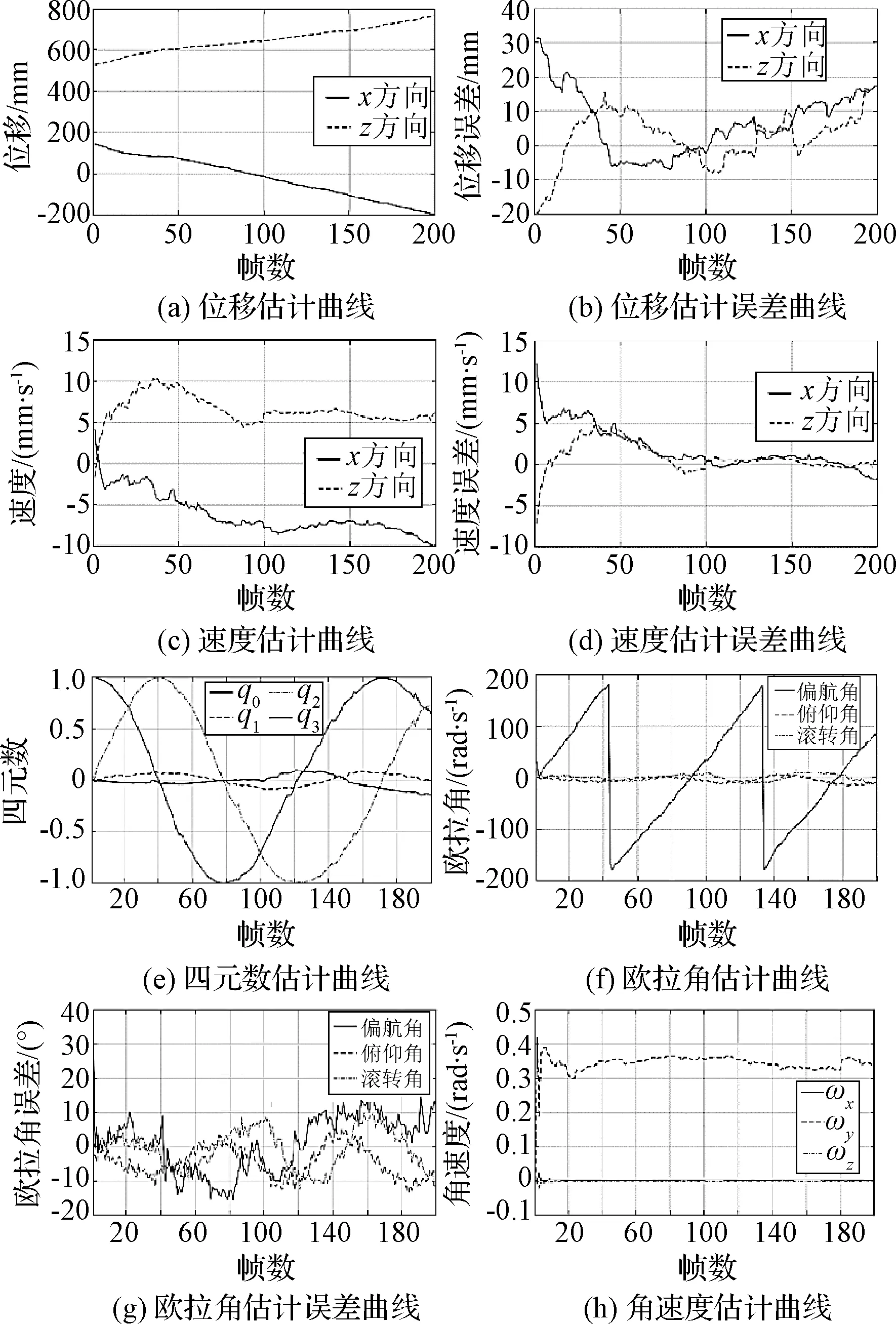
图15 复合运动估计结果Fig.15 Estimation results of compound motion

4.3目标结构点估计

试验中得到的目标点云含有少量背景特征点及观测次数较少的目标特征点，试验设定只在MATLAB中绘制观测次数大于5次的特征点。图16(a)～16(f)为复合运动下对目标进行三维稀疏点云重构的过程，最终得到的数据点个数为2870。图16(g)～16(i)分别为200帧时目标点云的x、y和z方向视图，根据最终点云结果，计算目标宽度为29 cm，与实际宽度30 cm相差1 cm；计算目标高度为18.5 cm，与实际高度20.5 cm相差2 cm。计算目标模型太阳能帆板长度和宽度分别为11.5 cm和4.5 cm，与实际长度12 cm和实际宽度3.9 cm接近。目标模型头部返回舱的计算高度和直径分别为4.2 cm和4.6 cm，实际高度和直径分别问6.5 cm和5 cm，主要是顶部特征不丰富，提取的特征点数量少。

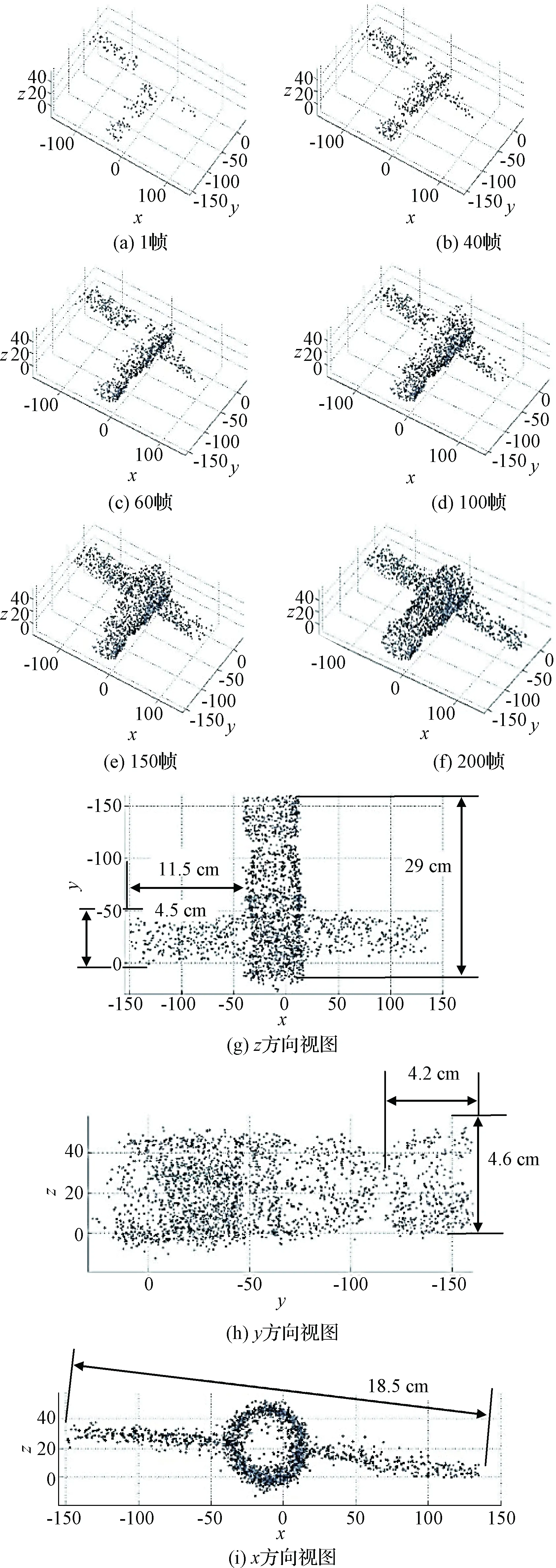
图16 目标结构估计结果Fig.16 Target structure estimation results

4.4结果分析

和仿真相比，参与Tri-EKF算法迭代的特征点数量远多于仿真试验，试验对目标运动估计收敛速度更快。此外，估计结果是所有特征点共同作用得出，少量特征点错误估计对最终估计影响较弱，系统估计稳定。但随着运动形式复杂度提高及特征点增多，收敛速度会降低。

试验估计曲线平滑度下降。仿真试验假设特征点匹配完全正确并能全部跟踪，噪声设定较理想。实际特征点会出现误匹配及跟踪丢失现象，还存在光照变化、设备测量及安装精度等因素，使得估计曲线平滑度下降。

估计变化曲线收敛后存在一段误差稳定阶段，该阶段内由于目标与相机间距离较近使得特征点三维坐标测量精度较高，因而算法能够对参数进行较稳定地估计。随着目标与相机间距离的增大，视觉系统测量噪声增大，估计误差出现小幅上扬趋势，算法估计精度随之降低。因此提高测量精度是提高估计精度的有效手段。

5 结 论

本文针对非合作目标运动和结构估计问题进行研究，建立了立体视觉系统数学模型，提出了Tri-EKF算法，该算法通过将特征线作为旋转观测量，实现了旋转与平移参数的解耦估计。通过仿真试验校验了Tri-EKF算法相比于传统的Dual EKF算法具有更快的收敛速度以及更小的有限次观测平均估计误差。在此基础上搭建了试验平台，并对本文算法进行校验。试验结果表明，Tri-EKF算法适用于不同目标运动形式，能够实现对目标的运动估计与结构估计。下一步研究方向将是在更多的运动自由度条件下进行运动估计以及结构稠密重建，深入开展运动参数及结构耦合程度的定性定量分析，使用GPU并行计算进行算法加速，提高算法实时性。

[1] 余江华. 非合作航天器相对位姿测量方法研究 [D]. 哈尔滨：哈尔滨工业大学, 2012. [Yu Jiang-hua. Research on relative position measurement of non-cooperative spacecraft [D]. Harbin: Harbin Institute of Technology, 2012.]

[2] Terui F,Kamimura H, Nishida S. Motion estimation to a failed satellite on orbit using stereo vision and 3D model matching [C]. The 9th International Conference on Control, Automation, Robotics and Vision, Singapore, December 5-8, 2006.

[3] Augenstein S, Rock S M.Improved frame-to-frame pose tracking during vision-only SLAM/SFM with a tumbling target [C]. IEEE International Conference on Robotics and Automation, Shanghai, China, May 9-13, 2011.

[4] Segal S, Carmi A, Gurfil P. Vision-based relative state estimation of non-cooperative spacecraft under modeling uncertainty [C]. 2011 IEEE Aerospace Conference, Mantana, USA, March 5-12, 2011.

[5] 蔡晗, 张景瑞, 翟光, 等. GEO非合作目标超近距相对位姿视觉测量 [J]. 宇航学报, 2015, 36(6):715-722. [Cai Han, Zhang Jing-rui, Zhai guang, et al. Relative pose determination for GEO non-cooperative spacecraft under the ultra-close distance [J]. Journal of Astronautics, 2015, 36(6):715-722.]

[6] 周军, 白博, 于晓洲. 一种非合作目标相对位置和姿态确定方法 [J]. 宇航学报, 2011, 32(3):516-521. [Zhou Jun, Bai Bo, Yu Xiao-zhou. A new method of relative position and attitude determination for non-cooperative target [J]. Journal of Astronautics, 2011, 32(3):516-521.]

[7] 翟光, 张景瑞. 空间非合作目标快速姿态跟踪导航方法研究 [J]. 宇航学报, 2013, 34(3):362-368. [Zhai Guang, Zhang Jing-rui. Research on rapid attitude tracking for space non-cooperative target [J]. Journal of Astronautics, 2013, 34(3):362-368.]

[8] 郝刚涛, 杜小平. 基于单目视觉图像序列的空间非合作目标相对姿态估计 [J]. 航天控制, 2014, 32(2):60-67. [Hao Gang-tao, Du Xiao-ping. Relative attitude estimation for space non-cooperative targets based on sequence of monocular images [J]. Aerospace control, 2014, 32(2):60-67.]

[9] Togneri R, Deng L. Joint state and parameter estimation for a target-directed nonlinear dynamic system model [J]. IEEE Transactions on Signal Processing, 2004, 51(12):3061-3070.

[10] Ljung L. Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems [J]. Automatic Control IEEE Transactions on, 1979, 24(1):36-50.

[11] Liu X, Escamilla-Ambrosio P J, Lieven N A J. Extended Kalman filtering for the detection of damage in linear mechanical structures [J]. Journal of Sound and Vibration, 2009, 325(4-5):1023-1046.

[12] Zhang H S, Negahdaripour S. EKF-based recursive dual estimation of structure and motion from stereo data [J]. IEEE Journal of Oceanic Engineering, 2010, 35(2): 424-437.

[13] Zhang H. Automatic sensor platform positioning and three-dimensional target modeling from underwater stereo sequences [D]. Miami:University of Miami, 2005.

[14] Diebel J. Representing attitude: euler angles, unit quaternions, and rotation vectors [J]. Matrix, 2006, 58(15-16): 1-35.

[15] 白渊杰. 基于加计阵列的飞行器姿态解算方法研究[D]. 西安：西安电子科技大学, 2014. [Bai Yuan-jie. Research on aircraft attitude algorithm based on the array of accelerometer[D]. Xi’an: Xidian University, 2014.]

[16] 郭本生. 基于立体视觉的非合作目标运动估计与结构估计方法研究[D]. 哈尔滨：哈尔滨工业大学, 2016. [Guo Ben-sheng. Research on motion and structure estimation methods of non-cooperative targets based on stereo vision[D]. Harbin: Harbin Institute of Technology, 2016.]

[17] Rublee E, Rabaud V, Konolige K, et al. ORB: an efficient alternative to SIFT or SURF [C]. IEEE International Conference on Computer Vision, Barcelona, Spain, November 6-11, 2011.

[18] Zhang D, Liang S, Zhang C, et al. 3D tree skeleton reconstruction based on enhanced PyrLK optical flow algorithm [J]. Journal of Computer-Aided Design and Computer Graphics, 2015, 27(7):1247-1254.

MotionandStructureEstimationofNon-CooperativeSpaceTargetBasedonTri-EKFAlgorithmandStereoVision

WANG Ke, YU Zhan-hai, LIU Hong, LI Rui-feng, GUO Ben-sheng

(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080，China)

For the motion state and structure estimation of a non-cooperative space target, the motion parameters are coupled, which leads to the slow convergence problem in the dual extended Kalman filter (Dual EKF) algorithm. In this paper, based on the stereo vision model, a feature line observation model is introduced for decoupling of the translational and rotational motion. Then the triple extended Kalman filter (Tri-EKF) algorithm is proposed to sequentially estimate the rotational, translational motion and structural parameters of the target. Compared with the Dual EKF algorithm, the simulation and experimental results prove that the Tri-EKF has a faster convergence speed on motion estimation and smaller average estimation error given limited observations.

Non-cooperative target; Tri-EKF algorithm; Motion and structure estimation; Stereo vision

V448

A

1000 -1328(2017)09- 0936- 10

10.3873/j.issn.1000-1328.2017.09.006

2016- 11- 02;

2017- 05- 24

国家自然科学基金创新群体基金(51521003)；黑龙江省自然科学基金(QC2014C072)；黑龙江省博士后基金(LBH-Z14108)

王珂(1979-)，男，讲师，主要从事机器人视觉技术，移动机器人SLAM，定位及导航等研究。

通信地址：哈尔滨市南岗区一匡街2号哈工大科学园C1栋305(150080)

电话：(0451)86418283

E-mail:wangke@hit.edu.cn

郭本生(1992-)，男，硕士，主要从事机器人视觉，运动目标检测等方面的研究。本文通信作者。

通信地址：哈尔滨市南岗区一匡街2号哈工大科学园C1栋501(150080)

电话：(0451)86418283

E-mail:gbs@hit.edu.cn