一种新的临空高超声速飞行器滑跃段跟踪算法

郭相科，付 强，范成礼, 韦 刚

(1. 北京航空航天大学电子信息工程学院，北京 100191;2. 空军工程大学防空反导学院，西安 710051)

一种新的临空高超声速飞行器滑跃段跟踪算法

郭相科1,2，付 强2，范成礼2, 韦 刚2

(1. 北京航空航天大学电子信息工程学院，北京 100191;2. 空军工程大学防空反导学院，西安 710051)

针对临空高超声速飞行器滑跃段跟踪中存在的跟踪不稳定问题，提出一种基于多传感器的多周期多模型估计的最大熵模糊数据关联滤波(MPMME-MEFPDAF)算法。首先，在临空高超声速飞行器滑跃段运动特性分析的基础上，采用多周期多模型估计方法实现模型集自适应。然后，采用最大熵模糊数据关联思想，解决杂波环境下多传感器航迹断续、点迹关联问题。最后，将多周期多模型估计与最大熵模糊概率数据关联相结合，实现临空高超声速机动目标的多传感器连续跟踪。通过仿真验证，该算法比传统算法对临近空间高超声速速飞行器滑跃段的跟踪具有更好的跟踪效果。

高超声速飞行器；机动目标跟踪；多周期多模型估计

0 引 言

以X-51A、HTV-2为代表的临空高速飞行器在整个飞行过程中，具有弹道导弹目标的高速特性，同时具有空气动力学目标的高机动特性，将成为未来空天角力中新一代战略威胁[1]，实现对其有效跟踪是拦截打击的基础与前提。

临近空间高超声速飞行器在滑跃阶段具有纵向大空域非线性不规则机动及横向机动的能力，且由于其高超声速飞行，RCS(Radar cross section)弱小，导致在目标的跟踪中存在跟踪不稳定。临空高速飞行器滑跃阶段具有纵向大空域机动、横向突变机动的特点，并且由于其高超声速飞行，RCS弱小，在单传感器跟踪中，存在断续航迹、点迹，容易淹没于噪声、杂波当中。临空高速飞行器滑跃段跟踪的主要难点在于如何实时准确的估计机动目标未知且快速变化的加速度，实现对非机动、弱机动跟踪精度和对强机动跟踪稳定性的统一，对运动模型及滤波算法均提出了很高的要求。文献[2]在高超声速目标助推-滑翔式运动特性分析的基础上，提出了一种LLA(Longitude-latitude-altitude)坐标系下基于目标特性分析的三维投影跟踪算法，通过仿真表明算法具有可靠的跟踪效果，但该方法具有一定的特殊性。文献[3]在高超声速目标滑跃式机动分析的基础上，建立了临空高速飞行器滑跃机动跟踪的Sine模型，并验证了该模型具有较好的跟踪效果，且该方法具有一定的普适性。文献[4-5]分析了高超声速目标的气动力模型，并分析了气动力模型的有效性。文献[4]在气动力学模型分析的基础上，推导了再入目标的Jerk动力学模型，建立了再入目标加速度递推模型，并根据随机模型近似思想给出了加速度过程噪声的两种定义。文献[6]将强跟踪算法与改进输入估计算法结合，提高了算法对目标强机动的反应能力。由于临空高速飞行器独特的机动样式，很难由一种模型完整覆盖其整个运动过程，且传统的交互多模型(Interactive multiple model, IMM)算法无法实时准确的选择匹配模型，导致无法稳定跟踪。多传感器协同是实现对其连续跟踪的可行思路，文献[7-8]分析了临空高超声速目标的多传感器跟踪方法的优越性。在考虑杂波环境下的数据关联问题时，文献[9]提出了杂波环境下混合模糊数据关联滤波算法，但计算量较大，难以应用于实际。因此，本文针对临空高速飞行器滑跃段机动的特点，采用多传感器协同跟踪，提出结合多周期多模型估计的最大熵模糊数据关联滤波算法(MPMME-MEFPDAF)，首先通过MPMME实现模型精选，再结合MEFPDAF思想，解决临空高速飞行器断续航迹、点迹关联问题，实现对其稳定跟踪。

1 滑跃段运动特性分析

临空高速飞行器的滑跃段是其主要运动阶段，其运动特征基本决定飞行器的射程，体现了这类目标的运动特点。在滑跃段，其飞行高度较高，机动过载不大，但气动参数变化复杂，导致其机动样式灵活，通常采用周期式或非周期式滑跃机动方式飞行[1-3]。针对滑跃段机动时跟踪，通常采用对气动参数进行建模的动力学模型和针对滑跃段机动特点建模的运动特性模型。但是由于机动不规则，不可能由某一种/几种模型完全覆盖，采用多模型构成模型集，并进行模型之间的实时切换的交互多模型是目前的主流方法。

因此，本文针对临空高速飞行器滑跃阶段的特点，考虑选取滑跃式机动Sine模型、Singer模型及分段Jerk自适应模型等构成模型集，进行滑跃段跟踪[3-4]。其中，Sine模型为加速度自相关函数为正弦波的零均值随机过程，可表述目标的规律跳跃的机动样式；Singer模型为加速度均值为零，且服从均匀分布的平稳时间相关函数，用于描述目标较为稳定滑翔阶段；分阶段Jerk自适应模型为加速度变化率为在采样间隔内均匀变化的随机过程，用于描述目标加速机动样式。

2 多模型多周期估计

由于临空高速飞行器滑跃段运动模式多变，很难对其运动参数进行实时精确估计，为覆盖其可能存在的各种机动状态，亟需采用多模型。同时，为了避免虚警导致跟踪错误，且满足目标机动与非机动状态的跟踪精度，考虑通过交互多模型理论及多模型自适应控制相结合，建立针对临空高速飞行器的多模型多周期自适应滤波算法。

通常，模型集中部分模型与当前目标运动状态不符时，会降低跟踪性能，并且模型太多使得模型间的竞争则会降低跟踪效果。多周期多模型滤波算法中，根据目标运动参数的变化范围，构建多个可能模型集合。利用获取的目标量测，根据模型切换准则对每个模型进行隶属判定，确定该目标量测对应的输出参考模型集。并依据每个时刻最优参数的变化，选取一个新的模型子集。在模型的切换中，为保障跟踪的实时性，并排除目标量测的随机误差和野值造成的跟踪错误，采用最近几周期的测量和自适应多模型滤波值分别求权，来确定选择模型集中的模型概率加权值[10]。

设目标状态方程与量测方程线性化为

(1)

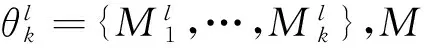
(2)

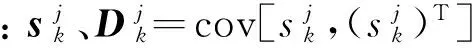
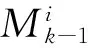
步骤 2.计算k时刻处于模型j，k-1时刻处于模型i的概率为

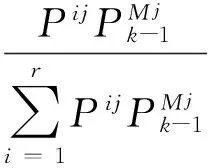
(3)

(4)

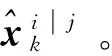
(5)

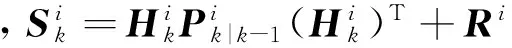
步骤 4.k时刻处于模型j的概率为

(6)

根据Bayes公式可得

(7)

将式(2)代入，得到

(8)

由式(2)与式(8)计算出目标k时刻多模型状态估计值：

(9)

3 基于最大熵模糊聚类的多传感器协同跟踪

模糊聚类是依据相似性将数据集分成子数据集的过程，在多传感器数据关联中，模糊聚类得到了广泛应用[13-15]。

3.1概率数据关联滤波器(PDAF)

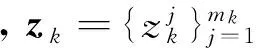
(10)

式中：Sk表示新息的协方差，小于g为有效观测。为估计关联概率，观测可由截止到前一时刻的累积观测集Zk-1及最新观测zk组成，关联概率为[13]

j=0,1,…,mk

(11)

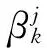
通过文献[14]的参数法，PDAF关联概率可通过以下计算

(12)

式中：

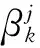
(13)

为改进PDAF性能，文献[15]提出适用于单目标跟踪的混合PDAF方法，在保持原框架不变的情况下，通过模糊c均值聚类(FCM)得到模糊隶属度替代关联概率，但是计算量较大，难以应用于实际，因此，本文通过最大模糊聚类原理实现目标的实时跟踪。

3.2概率最大熵模糊聚类原理

设N个观测数据为{xi,i=1,2,…,N},c类,{cj,j=1,2,…,c},可描述聚类过程为以下优化过程，代价函数为

(14)

式中：d(xi,cj)为xi与聚类中心cj的欧氏距离，ui|j为xi属于cj的概率，并且ui|j服从约束如下

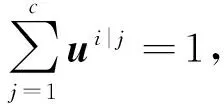
(15)

为最小无偏描述xi与cj的隶属度，可通过最大熵原理将熵最大化。依据香农熵准则，表达式为：

(16)

通过式(14)与式(15)的约束，使式(16)最大，通过拉格朗日乘子法，目标函数定义如下：

(17)

αi为拉格朗日乘子，λi为杂波密度。可通过变化αi改变观测数据xi与各类中心的隶属度值，可称αi为差异系数。使目标函数值最大化，则数据点与各类之间的隶属度可记为

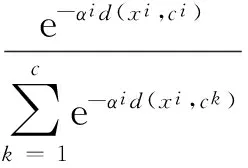
(18)

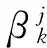
(19)

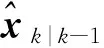
(20)

3.3系统模型及量测模型建立

1)系统模型

考虑离散系统模型如下：

(21)

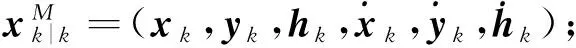
2)红外传感器量测模型

红外传感器可获得目标的高低角ek+1与方位角ak+1信息，其在UEN坐标系下的非线性量测方程表示为：

(22)

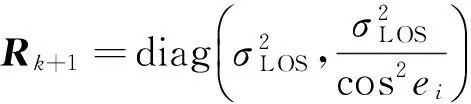
其中，以空基红外传感器作为坐标原点，以地心与传感器连线的延长线方向作为U轴，N轴位于U轴和地球自转轴组成的平面内，指向正北，与U轴正交，E轴指向正东，通过右手准则确定。

3)雷达传感器量测模型

非线性量测模型为：

式中：ak+1为方位角，ek+1为俯仰角，Vk+1表示方差矩阵为Rk+1的高斯量测噪声。

需要注意的是，在两种传感器维数不同时，将两种传感器对应的量测分量进行融合，缺失的分量无法融合，直接运用雷达量测。这样，不确定空气动力参数条件下的临空高速飞行器跟踪问题就转化为了一个非线性的滤波问题，需要使用非线性的滤波技术来解决此类问题。

3.4结合多周期多模型估计的最大熵模糊概率数据关联滤波算法

将MPMME与MEF-PDAF结合，提出一种在杂波环境下可行的目标机动跟踪滤波方法，即MPMME-MEFPDAF。根据MPMME的方法完成模型集更新，完整循环的算法处理步骤如下：

1)交互与初始化

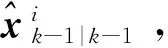
(24)

初始状态协方差为

(25)

2)预测

(26)

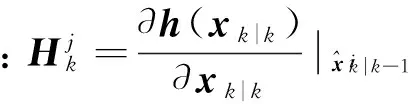
3)确认观测

(27)

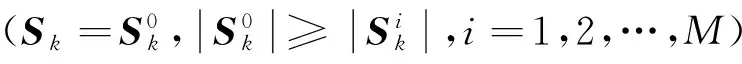
4)概率模型更新

由下式可得在k时刻模型i的正确概率

(28)

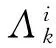
Vk-mkγ0[mk]+

(29)

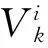
(30)

5)滤波与融合

通过MEF-PDAF，对模型i的进行状态更新

(31)

通过下列方程分别进行状态估计与状态协方差更新：

(32)

4 仿真校验与分析

在两个跟踪传感器条件下，验证临空高速飞行器滑跃段跟踪情况，目标运动轨迹的按照文献[17]中临近空间高超声速目标的动力学模型进行再入段的运运动仿真。为简化场景设置，假设雷达观测位置与飞行器运动轨迹均位于垂直于地平面的平面内，红外传感器(定点浮空观测)轨道高度60 km，测量误差为50 μrad。雷达传感器位于坐标原点，距离量测标准差σr=50 m和角度量测标准差为σE=0.01°，固定杂波密度λ=1，探测周期0.5 s。图1(a)～(c)分别为临空高速飞行器高度、速度和航迹角随时间变化情况。

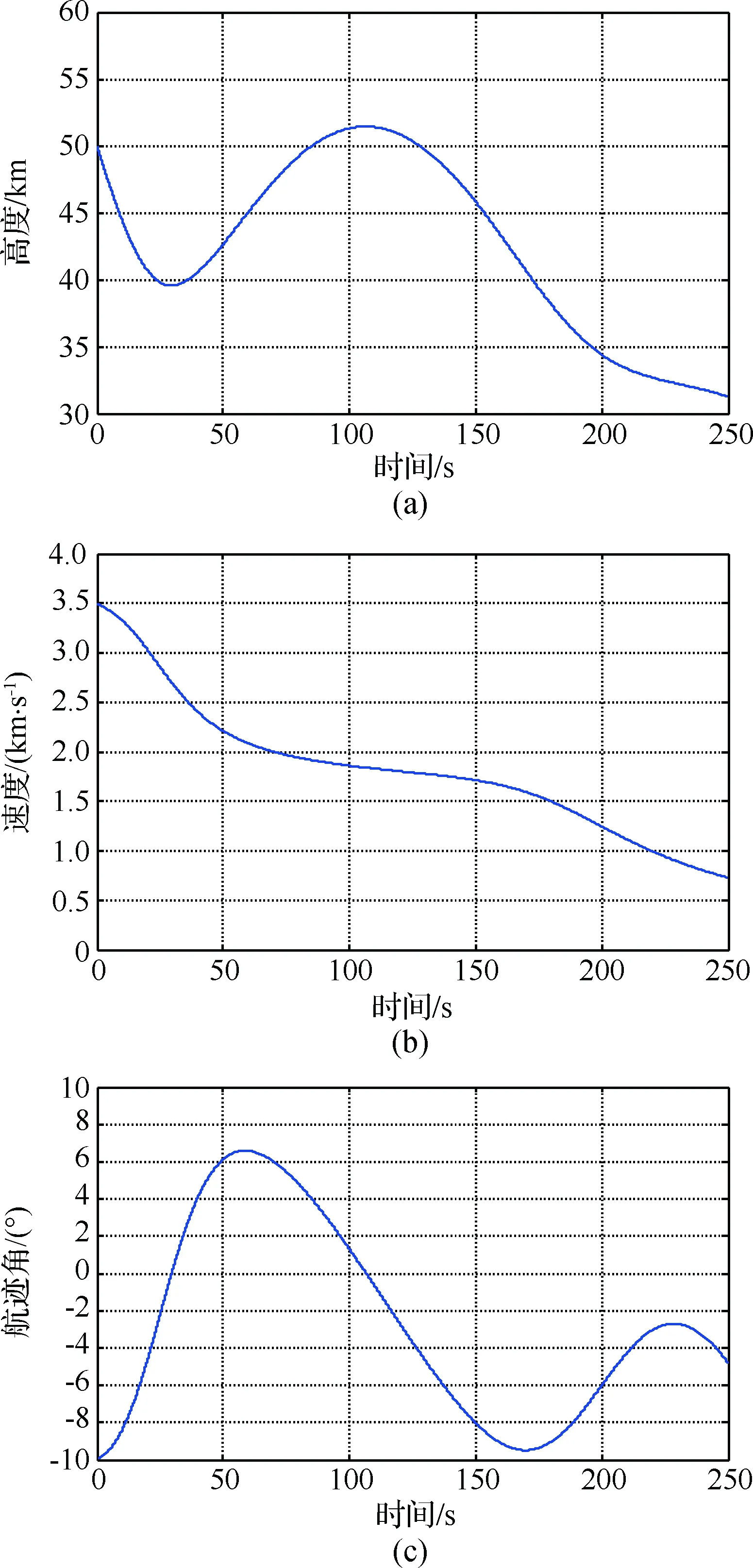
图1 目标状态随时间变化曲线Fig.1 The curve of target state change with time

为检验本文跟踪算法的有效性，本文算法分别与IMM-PDAF和最大熵模糊聚类IMM-MEFPDAF算法进行比较。

Di∈{0.2,0.55,0.9,1.3,1.6,2.1}×CLj∈{0.25,2,4,6,8,10}×C,C=3.734×10-5

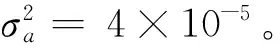
图2是三种算法的位置估计均方根误差，从图2可以看出，三种算法在目标发生滑跃机动时都存在跟踪误差，但本文提出的MPMME-MEFPDAF算法位置误差与IMM-MEFPDAF算法相比精度更高，两种算法都比IMM-PDAF算法性能优势明显。图3是三种算法的速度均方根误差，从图可知，在飞行器发生跳跃机动初始时误差较大，但逐渐收敛，本文提出的MPMME-MEFPDAF算法跟踪精度比IMM-MEFPDAF和IMM-PDAF有明显优势。

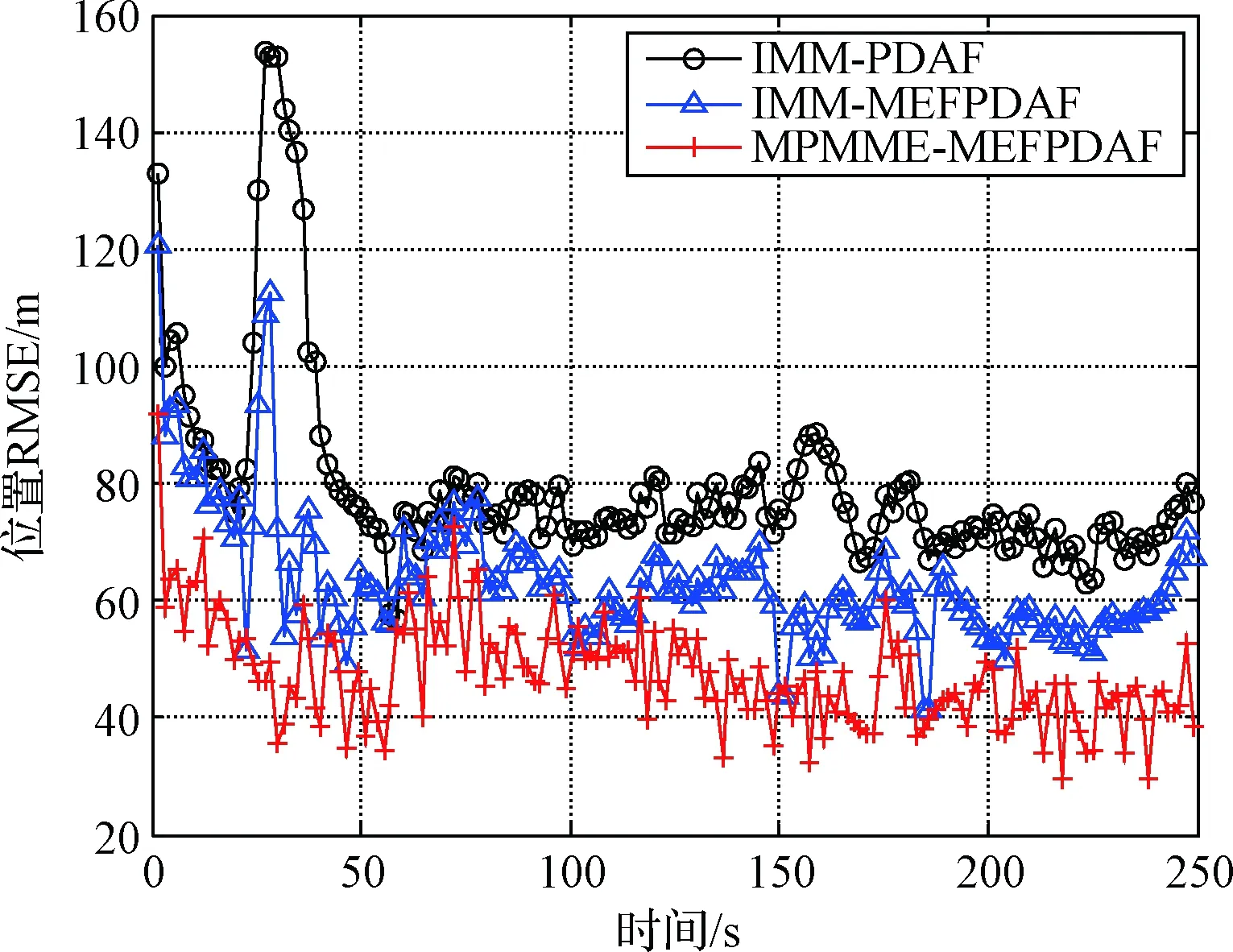
图2 位置估计均方根误差Fig.2 Position estimation root mean square error

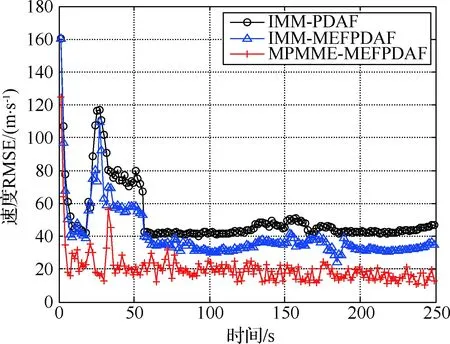
图3 速度估计均方根误差Fig.3 Vector estimation root mean square error

表1是本文算法与IMM-PDAF算法进行100次Monte Carlo仿真的计算性能对比，通过仿真结果可知，本文算法在精度上要高于IMM-MEFPDAF算法,后者的跟踪精度高于传统IMM-PDAF算法。并且本文算法耗时更少，主要原因是本算法能将一些无效观测信息有效的剔除，而这些信息在IMM-PDAF算法中通常被当成是有效观测。

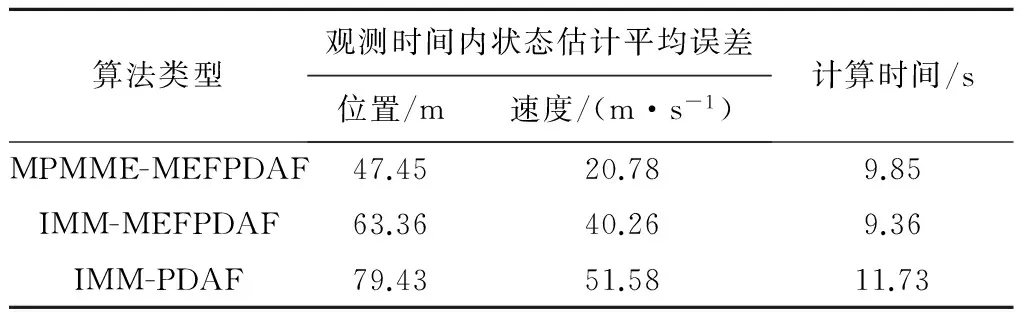
表1 算法性能对比

5 结 论

针对临空高速飞行器滑跃段模型集复杂，易受杂波影响的特点，提出了MPMME-MEFPDAF算法，可实现模型的有效精选，提高断续点迹的关联效果。通过仿真对比表明，本文所提算法能实现对临空高速飞行器滑跃阶段的稳定跟踪，并且时效性较好。为未来反临近空间高超声速目标探测跟踪提供了一种有效的理论方法。

[1] 李淑艳, 任利霞, 宋秋贵, 等.临近空间高超音速武器防御综述[J]. 现代雷达,2014, 36(6):13-18. [Li Shu-yan, Ren Li-xia, Song Qiu-gui, et al. Overview of anti-hypersonic weapon in near space [J]. Modern Radar, 2014, 36(6): 13-18.]

[2] 张翔宇, 王国宏, 张静, 等.临近空间高超声速助推-滑翔式轨迹目标跟踪[J]. 宇航学报, 2015, 36(10):1125-1132. [Zhang Xiang-yu, Wang Guo-hong, Zhang Jing, et al. Tracking of hypersonic boost-to-glide trajectory target in near-space [J]. Journal of Astronautics, 2015, 36(10): 1125-1132.]

[3] 王国宏, 李俊杰, 张翔宇. 临近空间高超声速飞行器滑跃式机动目标的跟踪模型[J]. 航空学报. 2015, 36(7):2400-2410. [Wang Guo-hong, Li Jun-jie, Zhang Xiang-yu. A tracking model for near space hypersonic slippage leap maneuvering target [J]. Ata Aeronautica et Astronautica Sinica, 2015, 36(7): 2400-2410.]

[4] Zhou Z, Liu J M, Gao Z C, et al. A variable structure multiple model algorithm with sojourn time conditions based on model augmentation [J]. ICIC Express Letters, Part B: Applications, 2013, 4(1): 141-148.

[5] 张凯, 熊家军, 韩春耀, 等. 一种基于气动力模型的高超声速滑翔目标跟踪算法[J].宇航学报, 2017, 38(2):123-130. [Zhang Kai, Xiong Jia-jun, Han Chun-yao, et al. A tracking algorithm of hypersonic glide reentry vehicle via aerodynamic model [J]. Journal of Astronautics, 2017, 38(2): 123-130.]

[6] Yang J L, Ji H B. High maneuvering target-tracking based on strong tracking modified input estimation [J]. Scientific Research and Essays, 2010,5(13): 1683-1689.

[7] 秦雷, 李君龙. 基于多站交互式多模型算法跟踪临近空间目标[J]. 系统仿真学报, 2014, 26(10): 2486-2496. [Qin Lei, Li Jun-long. Research on multi-station tracking for near space target based on IMM algorithm [J]. Journal of System Simulation, 2014, 26(10): 2486-2496.]

[8] 刘源, 张翔宇, 王国宏, 等. 基于雷达协同组网的高超声速目标跟踪算法[J]. 计算机仿真, 2016, 33(4): 36-40. [Liu Yuan, Zhang Xiang-yu, Wang Guo-hong, et al. A tracking algorithm of hypersonic target based on radar cooperative network [J]. Computer Simulation, 2016, 33(4): 36-40.]

[9] Li L Q, Ji H B. A novel maneuvering target tracking algorithm with two passive sensors[C]. The 8th International Conference on Signal Processing, Guilin, China, November 16-20, 2006.

[10] Dong L P, Yun F G. Fuzzy-logic adaptive variable structure multiple-model algorithm for tracking a high maneuvering target [J]. Journal of the Franklin Institute. 2013, 21(9): 11-21.

[11] Guo Z, Li S, Wang X. Distributed point-based gaussian approximation filtering for forecasting-aided state estimation in power systems [J]. IEEE Transactions on Power Systems, 2015, 69(9): 1-12.

[12] Li H N, Lei H M, Zhai D L, et al. Tracking oriented dynamics modeling of airbreathing hypersonic vehicles [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1651-1664.

[13] Yener U, Bilge G. Multiple model target tracking with variable rate particle filters [J]. Digital Signal Processing, 2012, 22(1):417-429.

[14] Li W L, Jia Y M. Distributed consensus filtering for discrete-time nonlinear systems with non-Gaussian noise [J]. Signal Processing, 2012, 92(10): 2464-2470.

[15] Shan M, Worrall S. Delayed-state nonparametric filtering in cooperative tracking [J]. Robotics IEEE Transaction on, 2015, 31:962-977.

[16] Li L, Xie W. Bearings-only maneuvering target tracking based on fuzzy clustering in a cluttered environment [J]. International Journal of Electronics and Communications, 2014, 68(2):130-137.

[17] Shen Z, Lu P. Dynamic lateral entry guidance logic [J]. Journal of Guidance Control & Dynamics, 2012, 27(6), 949-959.

ANewTrackingAlgorithmforNearSpaceHypersonicVehicleinGlidingJumpingPhase

GUO Xiang-ke1,2，FU Qiang2，FAN Cheng-li2，WEI Gang2

(1. School of Electronic and Information Engineering, Beihang University, Beijing 100191, China; 2. School of Air And Missile Defense, Air force Engineering University, Xi’an 710051, China)

To improve the tracking accuracy of a near space hypersonic vehicle, a multi-period and multi-model estimation maximum entropy fuzzy data association filter (MPMME-MEFPDAF) algorithm based on multiple sensors is proposed. Firstly, according to the characteristics of the hypersonic vehicle in the gliding jumping phase, the multi-period-multi-model estimation (MPMME) is adopted to realize the model adaptation. Secondly, the maximum entropy fuzzy data association filter (MEFPDAF) is considered to solve the problems of the discontinuous trajectory and point correlation in the clutter environment. Finally, the MPMME-MEFPDAF algorithm, combined with the MPMME and MEFPDAF, is used to complete the tracking of the near space hypersonic maneuvering target. The simulation results show that the proposed algorithm has better tracking effect than the traditional algorithm in the gliding jumping phase.

Hypersonic vehicle; Maneuvering target tracking; Multi-period-multi-model estimation

TP391

A

1000-1328(2017)09- 0971- 08

10.3873/j.issn.1000-1328.2017.09.010

2017- 03- 13;

2017- 07- 17

国家自然科学青年基金(61503408)

郭相科(1980-)，男，博士生，主要从事多源信息融合，机动目标跟踪方面研究。

通信地址：陕西省西安市长乐东路甲字1号(710051)

电话：(029)84789391

E-mail：guosyanyu@163.com

付强(1988-)，男，博士，主要从事非线性滤波算法研究。本文通信作者。

通信地址：陕西省西安市长乐东路甲字1号(710051)

电话：(029)84789289

E-mail：fuqiang_66688@163.com