仅测角导航多约束交会的闭环最优制导

罗建军，吕东升，龚柏春，殷泽阳

(1. 西北工业大学航天学院，西安 710072；2. 航天飞行动力学技术重点实验室，西安 710072；3. 南京航空航天大学航天学院，南京 210016)

仅测角导航多约束交会的闭环最优制导

罗建军1,2，吕东升1,2，龚柏春3，殷泽阳1,2

(1. 西北工业大学航天学院，西安 710072；2. 航天飞行动力学技术重点实验室，西安 710072；3. 南京航空航天大学航天学院，南京 210016)

针对多目标、多约束仅测角导航自主交会闭环最优制导问题，提出一种基于凸优化方法的最优制导算法。首先，考虑可观测性和鲁棒性要求，建立仅测角导航与制导多目标优化的性能指标，在此基础上，确立多目标、多约束最优交会问题的目标函数，以及基于凸优化的最优制导问题求解方法；然后，根据仅测角相对导航和制导之间存在的“耦合”关系提出了仅测角导航闭环制导的框架和解决方案；最后，仿真分析可观测性对导航和制导性能的影响，验证了所提出的仅测角导航多约束交会闭环凸优化制导方法的有效性。

可观测性；多约束；鲁棒性；凸优化；闭环制导

0 引 言

相对导航与制导是航天器在轨自主服务领域和航天器自主捕获与交会任务中的关键技术[1-2]。目前一些用来测量相对运动信息的主动有源式导航传感器，例如微波雷达、激光雷达等，由于体积大、功耗高、质量大和成本高等因素，在未来的非合作目标自主捕获与交会应用中会受到很大限制，而基于角度信息测量的光学相机等无源被动式传感器在这一方面却有很大的优势和应用前景[3-4]，瑞典的PRISMA计划[5]对基于测角信息的相对导航与制导技术进行了部分验证，美国的Raven计划也将在近期对这一技术进行验证。

仅基于角度信息的仅测角相对导航会存在状态不可完全观测的问题，目前主要采用相机偏置法、复杂动力学法和轨道机动法等方式来提高状态的可观测性，但是相机偏置法尽管实现方式简单却存在适用距离受限的缺点[6]，复杂动力学法尽管可以解决不可观测的问题，却存在易受噪声干扰、不适用于近程交会的缺点[7]。相互比较而言，尽管轨道机动法会增加燃料消耗并使得导航与制导性能直接受到交会轨迹的影响，但是其应用范围不受限，实现简单[8]。因此，国内外学者对仅测角导航情况下的最优交会导航与制导问题进行了研究。Oshman等[9]和Fosbury等[10]以费舍尔信息阵和估计协方差为优化指标，研究了交会过程中可观测性最优情况下的数值优化问题，但存在数值优化问题求解难度大的不足；Pi和Bang[11]研究了可观测性最优和可观测性限制条件下燃料最优两种情况下的仅测角相对导航机动轨迹设计问题，但存在可观测性指标和可观测性不一致的问题，且没有考虑到在线优化；Luo等[12]则研究了多脉冲滑移制导情况下，仅测角相对导航和制导之间的耦合关系，并通过仿真结果对其做了说明，但也没有考虑交会过程中存在的各种约束和制导优化问题。D’Amico等[13]研究了具备可观测性的交会轨迹，但是所有的机动都是离线设计的。Ponda等[14]研究了无人机仅测角导航可观测性最优的制导轨迹设计问题，最终的螺旋轨迹能够保证无人机在接近目标的过程中具备一定的可观测性，同时降低了不确定性，但是并没有考虑到过程中多种约束的存在。总的来说，目前的研究主要集中在提高仅测角导航可观测性的机动轨迹设计、可观测性最优下的制导轨迹设计，缺乏对同时满足可观测性和燃料消耗最小需求下的多约束仅测角最优制导，以及导航与制导一体化的闭环最优鲁棒制导的研究，不能满足实际交会过程的需要。

本文从综合考虑可观测性和燃料消耗，以及实现多约束闭环在线最优交会鲁棒制导的目的出发，研究了仅测角导航多约束闭环最优交会制导问题，首先给出了空间交会过程中的性能指标和各种约束，确立了多目标、多约束优化问题的表述形式，并引入凸优化算法[15]对多约束最优制导问题进行在线实时求解，然后根据仅测角相对导航和制导之间存在的“耦合”关系设计了导航与制导一体化的闭环制导方案，最后进行了数值仿真校验。

1 问题描述

在空间交会任务中，如果要通过仅测角的方式来为追踪星实现导航，就会存在相对状态不可观测的问题。若采用轨道机动的方式来解决不可观测问题，就会额外消耗燃料，因此可观测性大小和燃料消耗之间是相互冲突的。本文旨在研究多约束条件下，以可观测性大小和燃料消耗为优化目标的多目标优化问题，得到一条既满足一定可观测性又确保燃料消耗相对较小的最优轨迹。本文选用C-W方程为空间交会的相对动力学模型[16]，其可以表示为：

(1)

2 性能指标

本节将分别建立燃料性能指标、可观测性性能指标以及误差协方差性能指标。

2.1燃料性能指标

一般来说，燃料消耗的多少与控制量(即机动u的范数)成正比，因此可以用所有机动的范数和作为燃料性能指标来反映实际燃料消耗的大小。燃料性能指标可以写为：

(2)

Jf=FTY

(3)

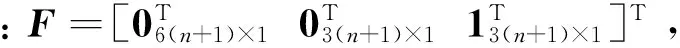
ui-si≤03×1

(4)

-ui-si≤03×1

(5)

2.2可观测性性能指标

可以根据轨道机动条件下的可观测性最优条件来建立交会优化过程中的可观测性性能指标[17]。采样时刻i的可观测性性能指标可以表示为：

(6)

式中：Φs=[ΦrrΦrv]是航天器交会相对运动状态转移矩阵Φ的一部分，Gr是推力驱动矩阵G中与位置状态相关的前三行向量所组成的矩阵。定义全局的可观测性为所有JOi的和，其在整个交会过程中可以写为如下的二次型形式：

(7)

式中：H是与Φs相关的矩阵。

2.3误差协方差性能指标

通过引入误差协方差来降低初始扰动对轨迹的影响，下面来构建误差协方差性能指标。

相对动力学方程的离散形式可以写为：

xk+1=Akxk+Bkuk+Γkωk

(8)

而标称轨迹可以表示为：

(9)

则离散的闭环误差协方差表示为：

(10)

给定初始误差协方差为

(11)

2.4优化目标函数

在建立了性能指标的基础上来讨论多目标优

化问题中的优化指标的组合形式[18]，采用最直观的加权求和形式，将多目标优化的目标函数表示为：

J′=w1Jo+w2Jf+w3Jp

(12)

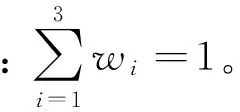
J=wJo+(1-w)Jf

(13)

并将误差协方差指标作为优化约束：

(14)

式中：Py是一个约束误差协方差大小的常数。

3 优化约束

在实际的空间交会过程中要综合考虑到各种约束的影响，尤其是对于交会过程中的优化问题来说，约束决定了优化问题的可行集。因此，有必要建立空间交会中存在的各种约束的模型。一般情况下，约束与具体的导航敏感器、目标以及交会场景有关。下面将建立空间交会任务中所涉及到的多种约束的凸化模型。

3.1相对动力学约束

根据式(1)可以得到离散的动力学方程：

xk+1-Φ(ΔT)xk-G(ΔT)uk=0

(15)

其中，ΔT表示的是采样时间间隔，令Y=[xTuTsT]T,则可以将式(15)表示为矩阵形式：

AEOMY=bEOM

(16)

式中：

(17)

同样可以得到边界约束条件为：

ABCsY=bBCs

(18)

式中：

(19)

(20)

3.2推力大小约束

推力大小约束是与航天器推力器相关的约束，可以表述为：

AuY≤bu

(21)

其中，

(22)

式中:umax和umin分别表示最大脉冲和最小脉冲。

3.3轨迹约束

在实际工程中，需要对追踪航天器的轨迹进行限制以使得追踪航天器不会越过目标的位置，这时就需要如下约束保证追踪航天器的轨迹满足要求：

AxY≤bx

(23)

其中,

(24)

式中:xmax和xmin分别表示轨迹约束的上、下界。

3.4视场约束

视场约束是一个顶点位于追踪航天器上的圆锥区域，以便保证目标处于追踪航天器的导航传感器视场范围之内。视场约束可以写为如下形式：

(25)

(26)

式中：

(27)

4 多约束闭环凸优化最优制导

4.1多约束凸优化最优交会制导问题描述

在建立了性能指标和约束并确定多目标优化问题目标函数的表示形式之后，基于凸优化方法的仅测角导航多约束交会最优制导问题最终可以写成：

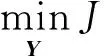
s.t.

本文采用凸优化的方法来求解多目标优化问题(28)，这是因为凸优化方法可以满足仅测角导航多约束交会最优制导中实时性的要求，同时所优化的目标函数固有的凸性可以确保有限次迭代后优化问题有解[15]。这样在整个交会过程中可以通过多次求解优化问题(28)来在线规划交会轨迹。

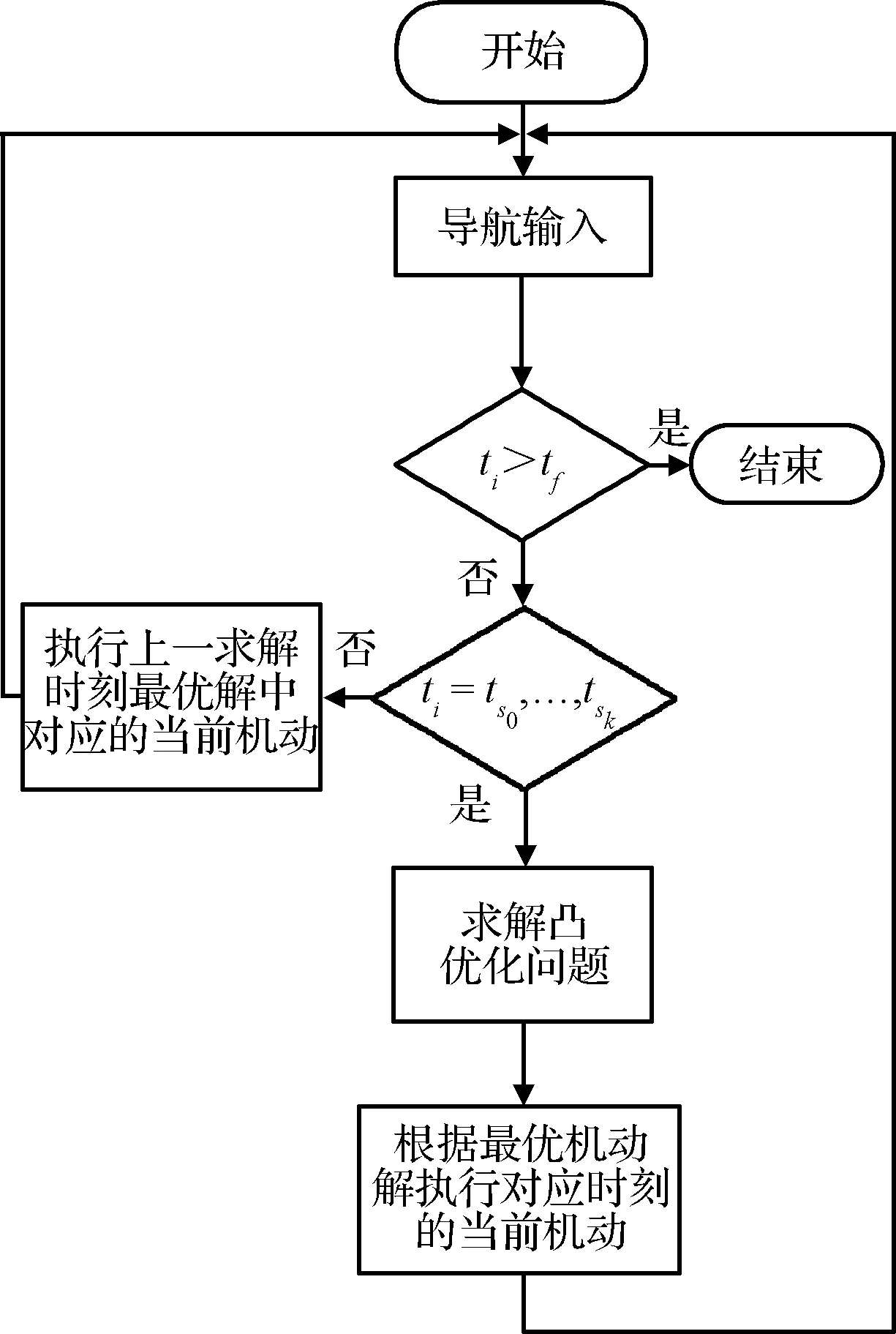
图1 凸优化最优制导流程图Fig.1 The flow chart of convex optimization optimal guidance

4.2仅测角导航闭环制导框架设计

注意到基于仅测角信息的自主交会导航和制导之间存在耦合的特点：一方面，导航信息是制导环节的输入，导航信息的误差影响着制导的精度；另一方面，对仅测角导航来说，机动的方式又可以提高导航的可观测性，使导航滤波结果更为精确，即制导影响着导航的精度。图2为闭环仅测角导航与制导的系统框图。

仅测角导航多约束交会的闭环最优制导的核心在于利用导航与制导的耦合属性来在线规划最优制导律。为此，本文设计了相对导航与闭环制导方案，其流程如图3所示。图中，ti和tf分别是当前采样时刻和终端时刻，P0是初始估计误差协方差矩阵，ΔV为制导速度脉冲，K表示滤波增益。从数据流上可以看出，“耦合”主要存在于导航系统估计相对运动状态并传递给制导系统；同时制导系统计算出速度脉冲ΔV并通过动力学方程来提高导航系统的可观测性。这里需要强调的是，由于多目标优化的问题存在可观测性性能指标，最优化解中的机动都是可观测的，并不需要做额外的可观测性判断。

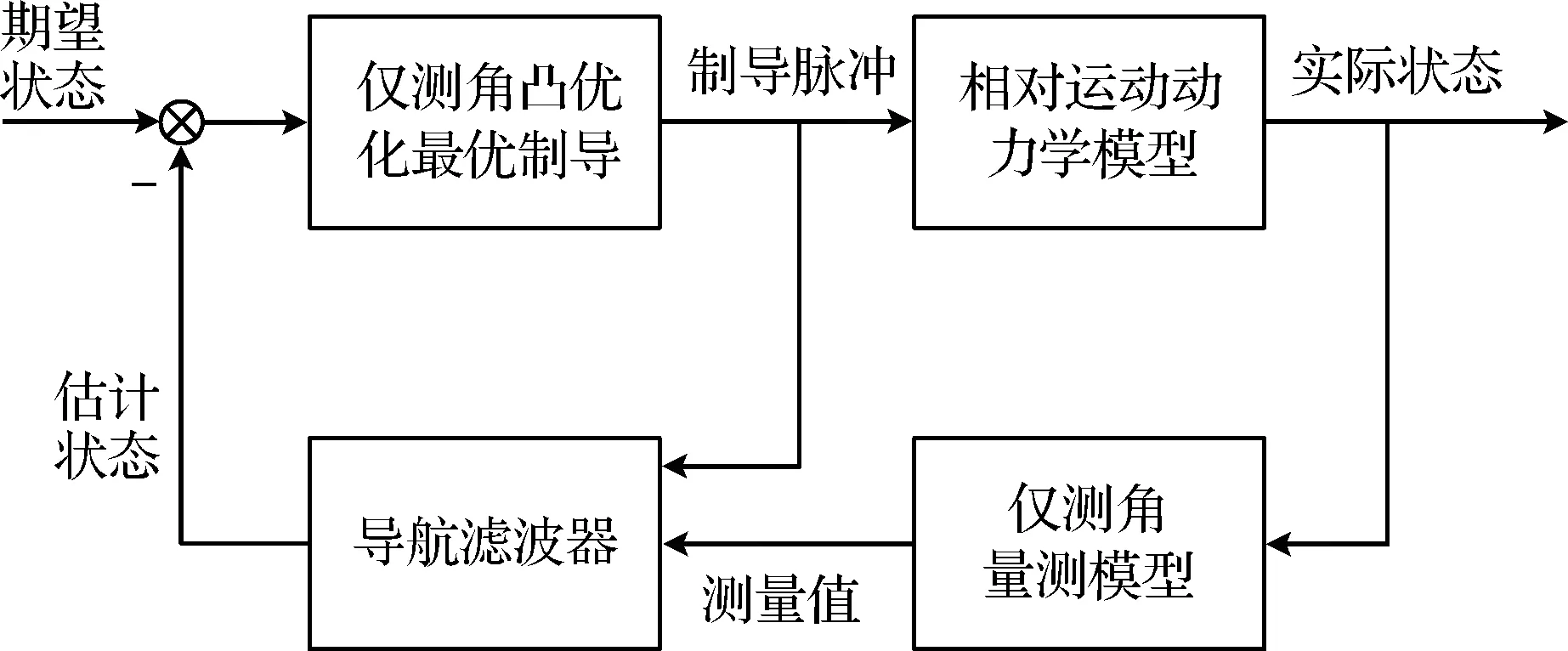
图2 闭环相对导航与制导系统框图Fig.2 The block diagram of closed-loop relative navigation and guidance system

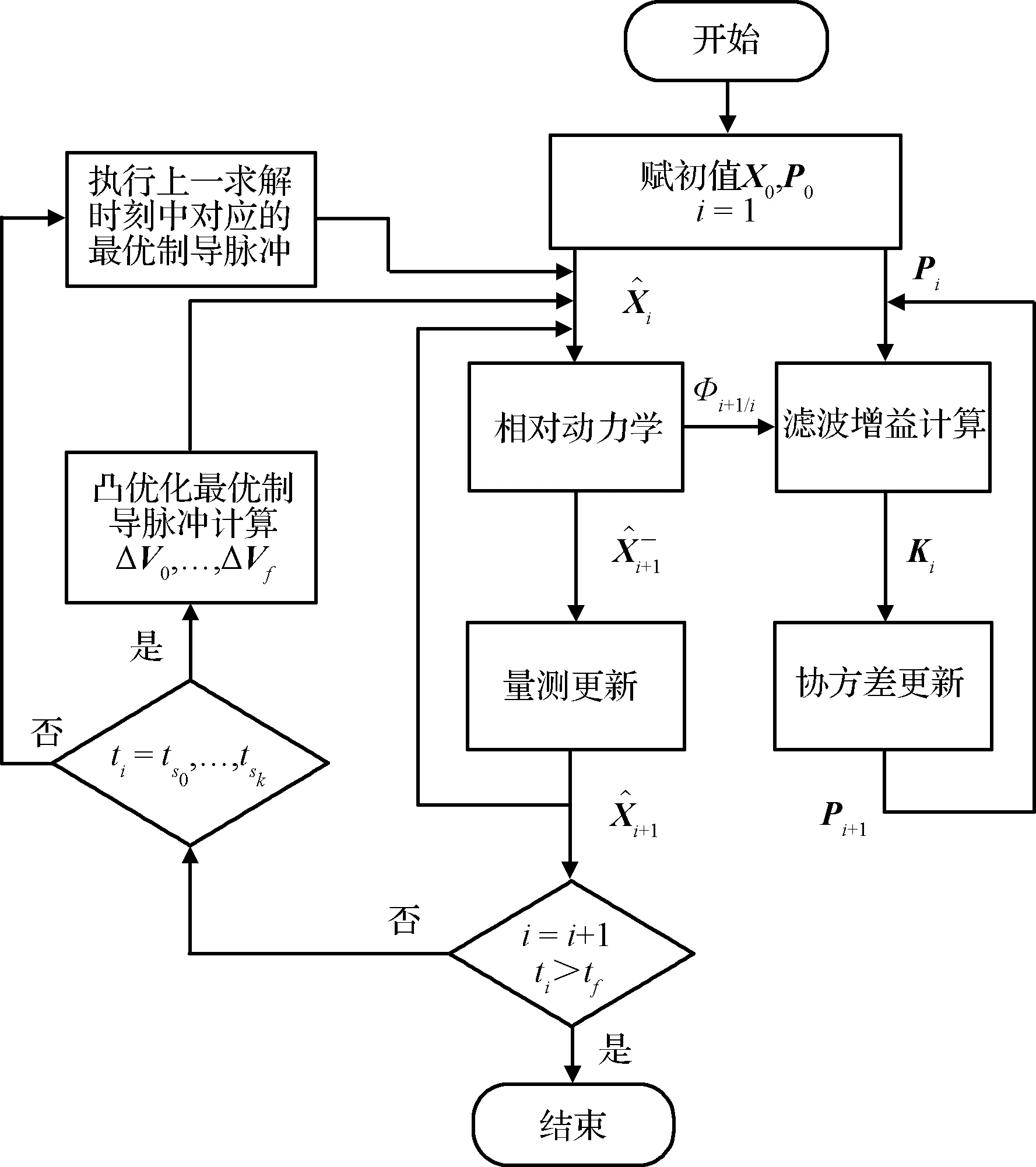
图3 闭环相对导航与制导算法流程图Fig.3 The flow chart of closed loop relative navigation and guidance algorithm

5 仿真分析

为了分析仅测角导航多约束闭环凸优化最优交会制导的特点和性能，本节分别从可观测性、燃料消耗以及鲁棒性三个方面进行了数值仿真。主要仿真参数设置如表1所示。

5.1可观测性仿真分析

图4表示采用不同大小的可观测性权重系数w针对优化问题(28)进行求解，得到的R-V平面和H-R平面内的不同制导轨迹。从图4可以看出，随着可观测性权重的提高，R-V平面内的轨迹在R-bar方向上的偏移距离越来越大。这是因为随着可观测性权重的提高，要求制导轨迹具备更高的可观测性，而根据向运动轨迹的垂直方向机动可观测性最大的原理，这意味着航天器要更多地向垂直于速度方向的R-bar运动以提高可观测性。

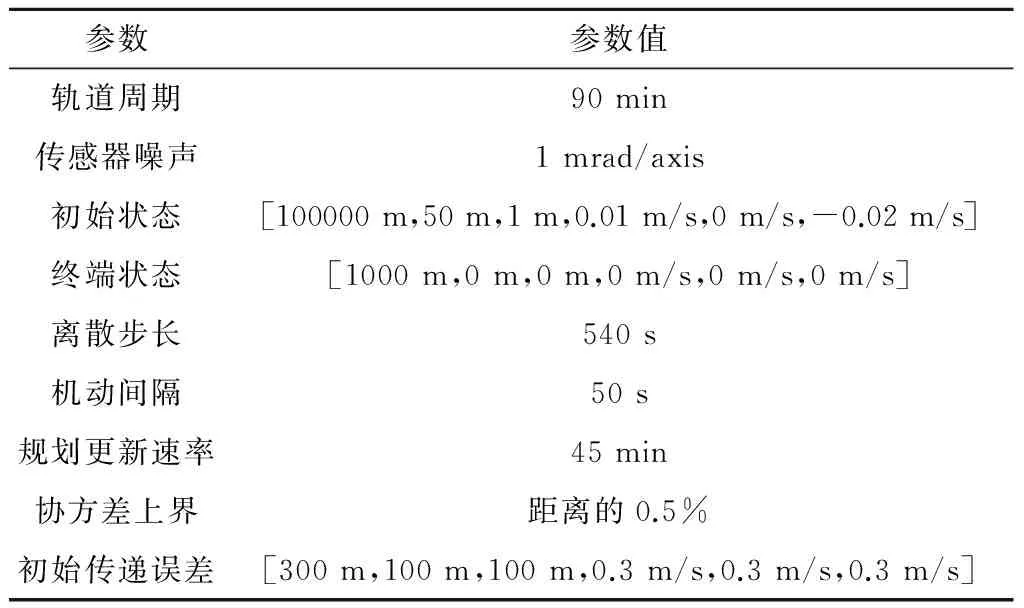
表1 主要仿真参数Table 1 The main simulation parameters

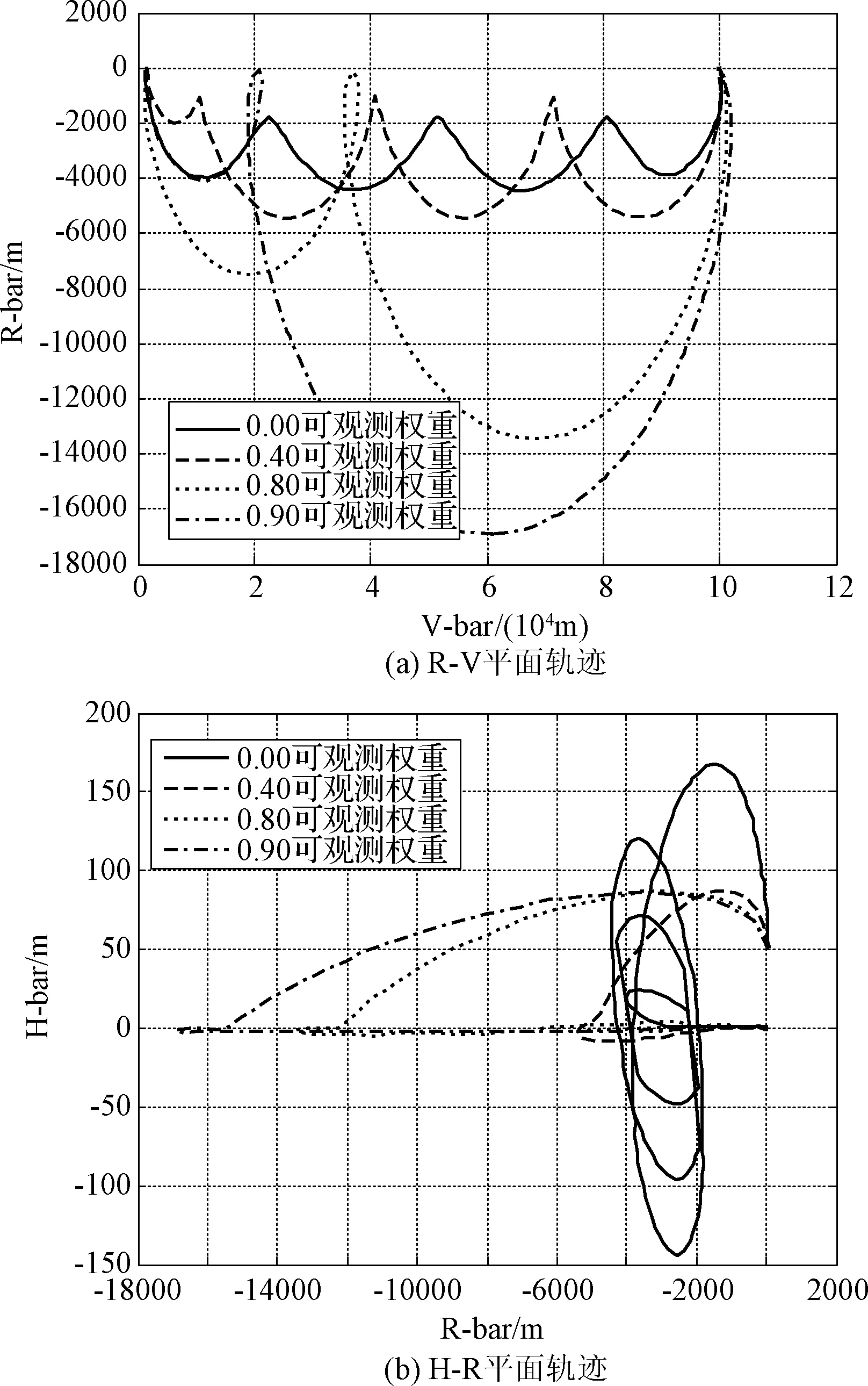
图4 可观测性对制导轨迹的影响Fig.4 Observability effect on guidance trajectory

图5和图6分别表示了100次蒙特卡洛仿真的燃料消耗统计与对应可观测性权重的关系以及导航误差统计与对应可观测性权重的关系。从图5可以看出，可观测性的权重系数和平均燃料消耗之间并不是线性关系，曲线的斜率是不断增大的，这意味着在可观测性权重增大到一定程度后，继续增加同样的可观测性要消耗更多的燃料。从图6可以看出，提高可观测性可以减小导航误差，改善导航性能，且当w大于0.6时，导航性能才会有明显的改善。

图5 可观测性与平均燃料消耗的关系Fig.5 The relationship between observability and average fuel consumption

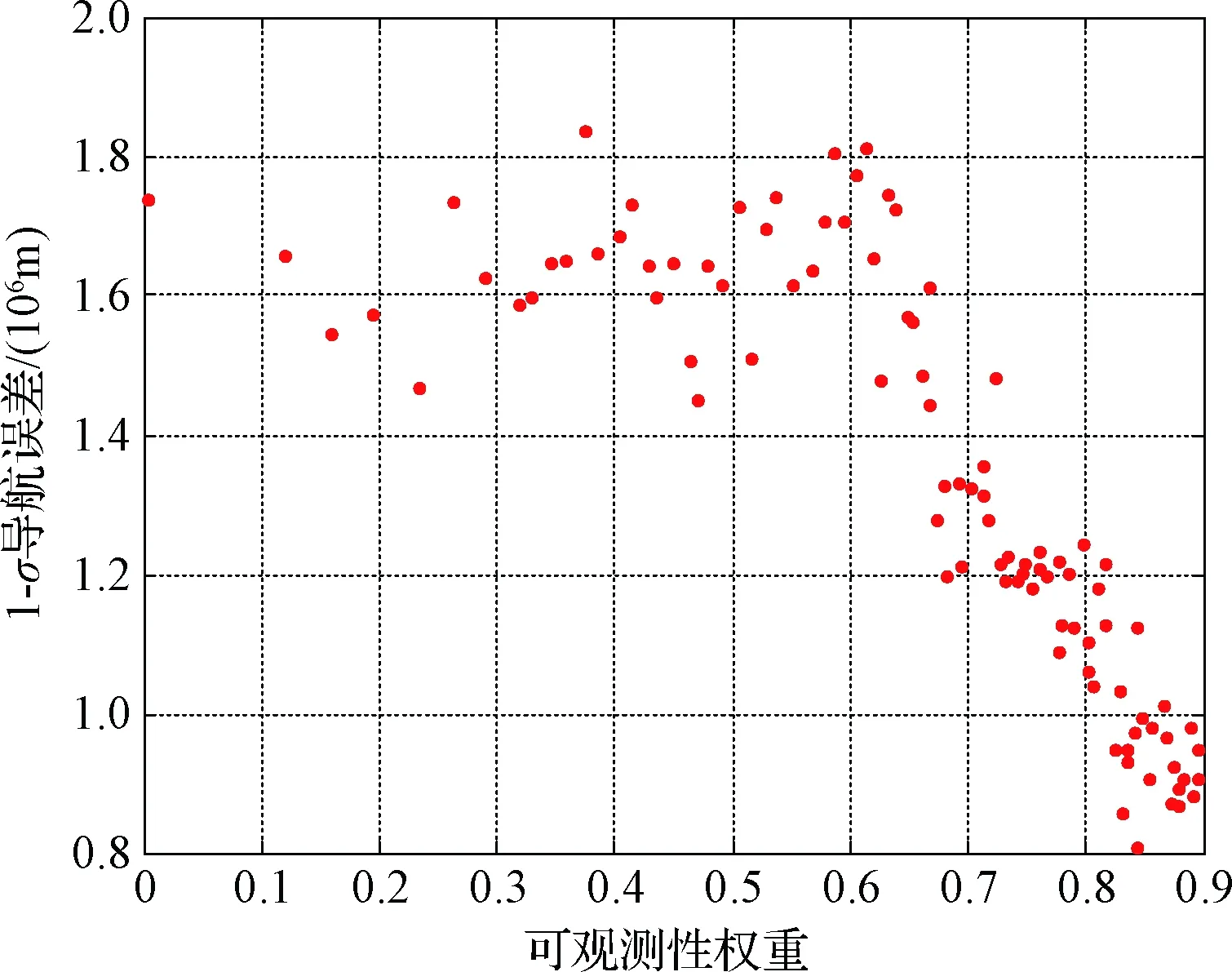
图6 可观测性与导航误差的关系Fig.6 The relationship between observability and navigation error

5.2燃料消耗仿真分析

从图7中总的趋势看，随着燃料消耗的增加，导航误差是降低的。从图8可以看出，随着平均消耗燃料的增加，终端导航误差呈现出先降后升的变化趋势。这是因为开始时随着可观测权重系数w的增加(导致平均燃料消耗也在增加)，导航性能是不断提高的，因此终端导航误差呈递减的趋势，但可观测性增加到一定程度后(即导航滤波器已经收敛时)，此时导航滤波器已经处于最优状态，大的脉冲机动反而会破坏当前状态，导致导航性能降低，因此终端导航误差会有上升的趋势。此外，终端制导误差和终端导航误差是成正比的(终端制导误差等于终端导航误差和控制误差之和)，因此考虑可观测性在一定范围内会提高终端制导精度。

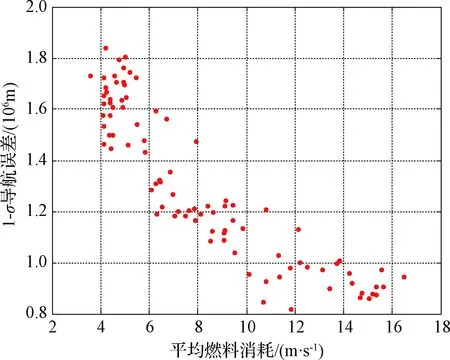
图7 平均燃料消耗与导航误差的关系Fig.7 The relationship between average fuel consumption and navigation error

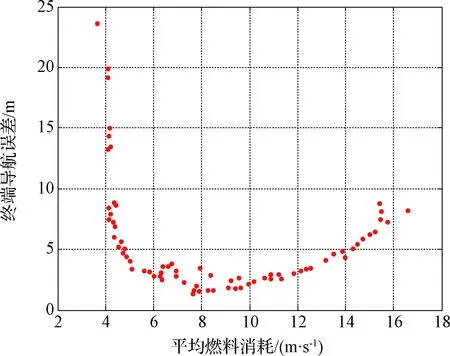
图8 平均燃料消耗与终端导航误差的关系Fig.8 The relationship between average fuel consumption and final navigation error

5.3鲁棒性仿真分析

本文引入了闭环误差协方差作为多目标优化问题(28)的一个约束来确保自主交会制导轨迹对初始扰动具备一定的鲁棒性，为分析和校验仅测角多约束闭环制导的鲁棒性，设计表2所示的工况进行仿真，并与不含误差协方差约束时的仿真结果做对比，其中工况2、3、4、5的初始位置和速度是分别相对于工况1而言的。

图9和图10分别表示含误差协方差约束情况下，初始条件在 5%左右变化时的R-V平面和H-R平面的轨迹。从图9～10可以看出，当存在初始扰动时，航天器的自主交会制导轨迹变化不大，基本上和未扰动情况下的轨迹重合。而从在不含误差协方差约束的图11～12中可以看出，在同等仿真工况下，R-V平面和H-R平面扰动轨迹与初始条件不存在扰动情况下的轨迹之间的分散程度要远大于含有误差协方差约束的情况，这一点在图12中尤为明显，说明引入误差协方差约束后可以增强自主交会制导轨迹的鲁棒性。

表2 w=0.9时的不同初始条件Table 2 Different initial conditions when w=0.9

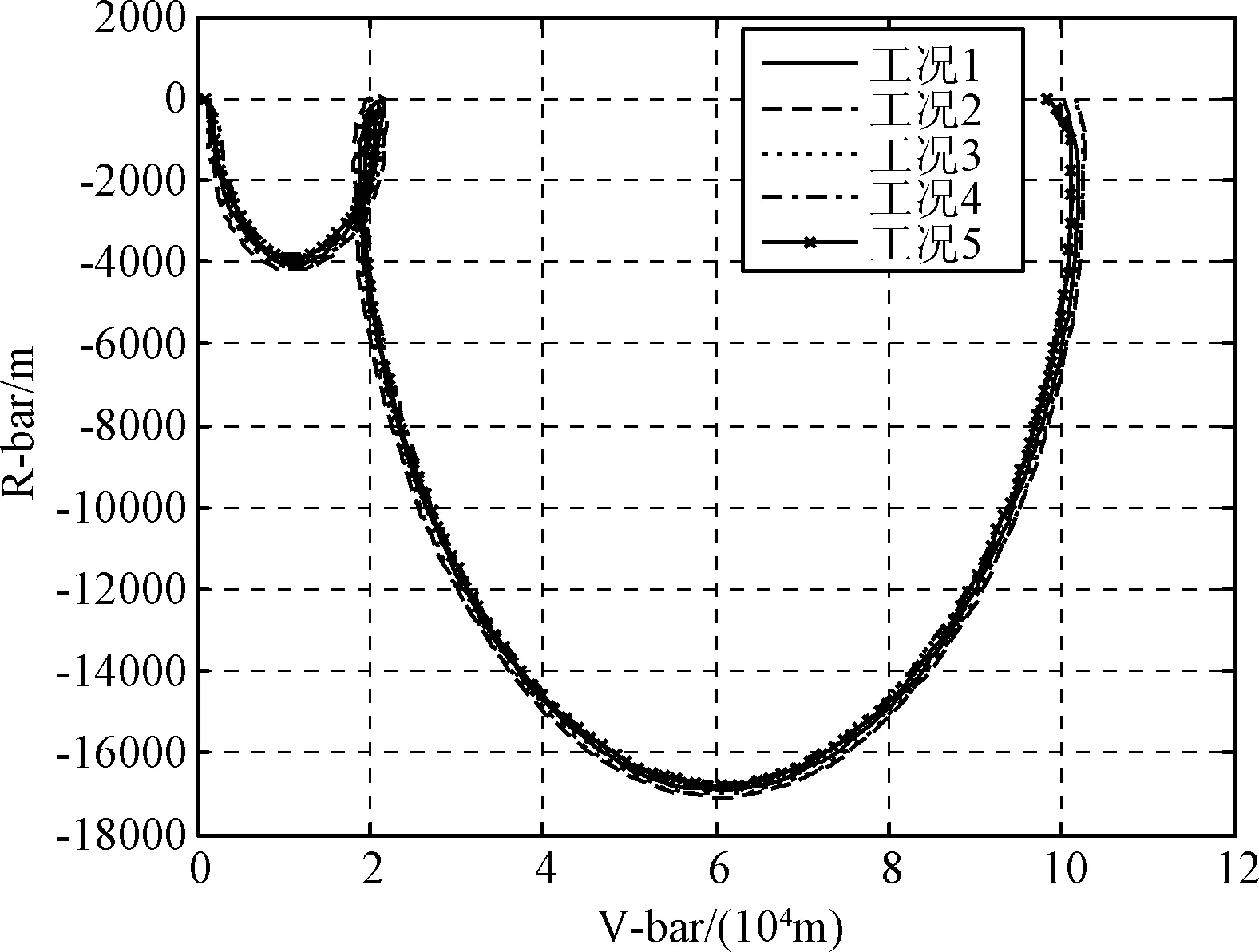
图9 w=0.9时不同初始扰动下的R-V平面轨迹(含误差协方差约束)Fig.9 R-V plane trajectories under different initial perturbations whenw=0.9(with error covariance constraints)

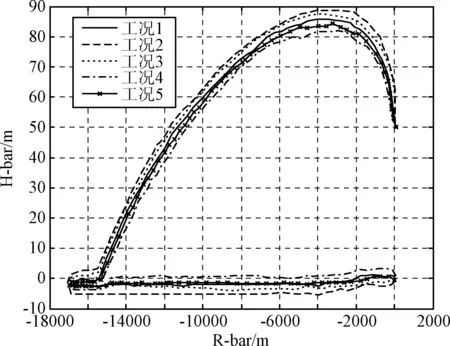
图10 w=0.9时不同初始扰动下的H-R平面轨迹(含误差协方差约束)Fig.10 H-R plane trajectories under different initial perturbations when w=0.9(with error covariance constraints)

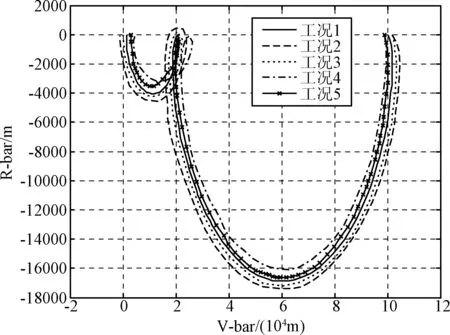
图11 w=0.9时不同初始扰动下的R-V平面轨迹(不含误差协方差约束)Fig.11 R-V plane trajectories under different initial perturbations when w=0.9(without error covariance constraints)

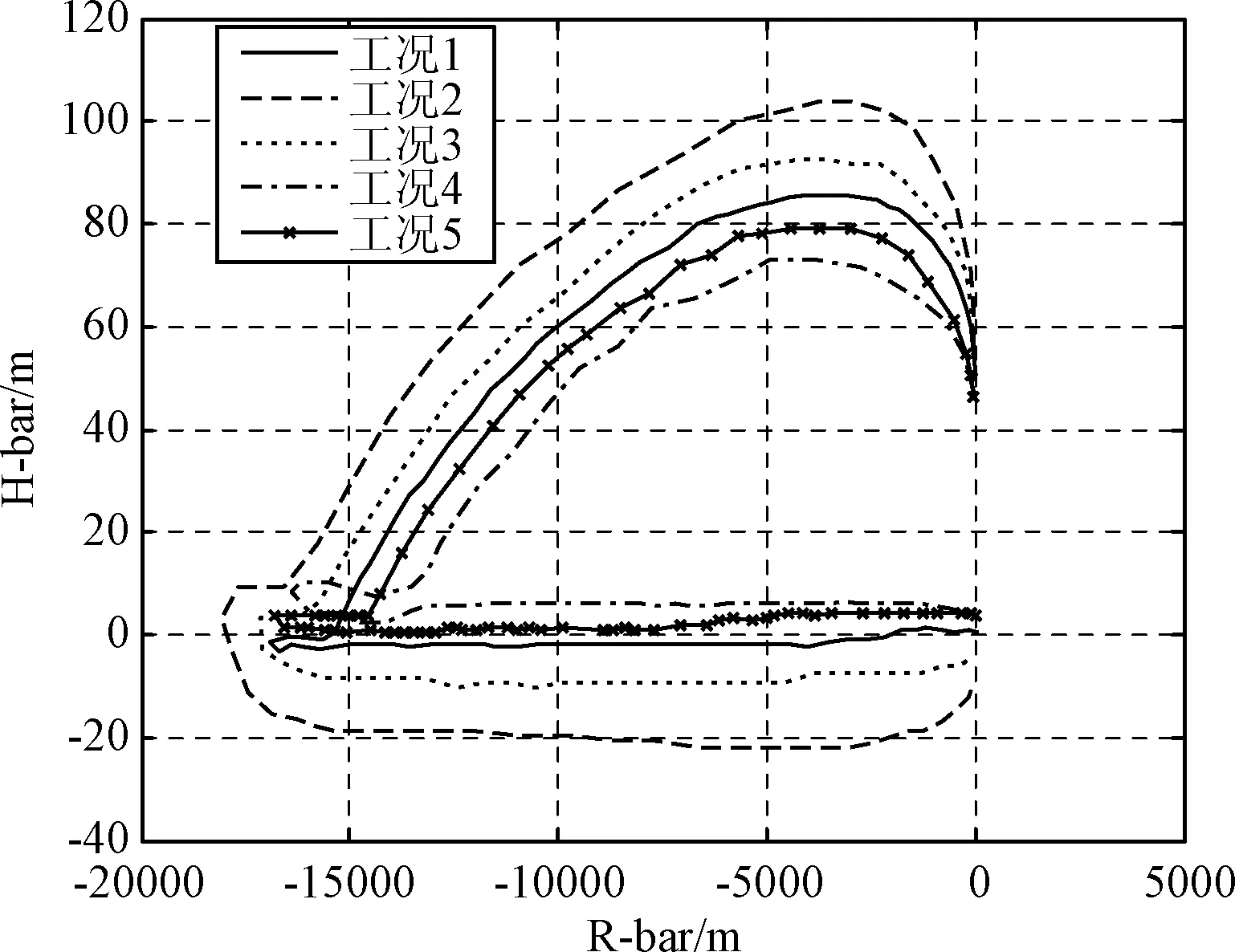
图12 w=0.9时不同初始扰动下的H-R平面轨迹(不含误差协方差约束)Fig.12 H-R plane trajectories under different initial perturbations when w=0.9(without error covariance constraints)

6 结 论

本文针对仅测角导航多约束闭环最优交会制导问题，提出了一种基于凸优化方法的最优制导算法，采用可观测性和燃料消耗作为优化指标，误差协方差作为约束，通过求解一个含多约束的多目标优化问题得到最优制导轨迹。数值仿真结果表明：

1)采用凸优化方法能够实时求解多约束下的多目标优化问题，并得到既能确保燃料消耗较小又能确保可观测性足够高的制导轨迹。

2)可观测性的提高可以有效地提升导航性能和终端制导精度。通过执行一系列可以提高观测性的机动就可以在只需要增加少量燃料消耗的情况下，加快导航误差协方差的收敛，并进一步降低导航误差和终端制导误差。

3)引入误差协方差约束能够确保制导轨迹相对于初始扰动具备一定的鲁棒性。

[1] 梁斌, 徐文福, 李成,等. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报, 2010, 31(1):1-13. [Liang Bin, Xu Wen-fu, Li Cheng, et al. The status and prospect of orbital servicing in the geostationary orbit [J]. Journal of Astronautics, 2010, 31(1): 1-13.]

[2] 崔乃刚, 王平, 郭继峰,等. 空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4):805-811. [Cui Nai-gang, Wang Ping, Guo Ji-feng, et al. A review of on-orbit servicing [J]. Journal of Astronautics, 2007, 28(4):805-811.]

[3] 梁斌, 何英, 邹瑜,等. ToF相机在空间非合作目标近距离测量中的应用[J]. 宇航学报, 2016, 37(9): 1080-1088. [Liang Bin, He Ying, Zou Yu, et al. Application of time-of-flight camera for relative measurement of non-cooperative target in close range [J]. Journal of Astronautics, 2016, 37(9): 1080-1088.]

[4] 李九人. 空间交会的仅测角相对导航与自主控制方法研究[D]. 长沙: 国防科学技术大学, 2011. [Li Jiu-ren. Research on angles-only relative navigation and autonomous control for space rendezvous [D]. Changsha: National University of Defense Technology, 2011.]

[5] Bodin P, Larsson R, Nilsson F, et al. PRISMA: an in-orbit test bed for guidance, navigation, and control experiments [J]. Journal of Spacecraft and Rockets, 2015, 46(3):615-623.

[6] Geller D K, Klein I. Angles-only navigation state observability during orbital proximity operations[J]. Journal of Guidance, Control and Dynamics, 2014, 37(6):1976-1983.

[7] Kaufman E, Lovell T A, Lee T. Nonlinear observability for relative orbit determination with angles-only measurements[J]. Journal of the Astronautical Sciences, 2016, 63(1):60-80.

[8] Grzymisch J, Fichier W. Observability criteria and unobservable maneuvers for in-orbit bearings-only navigation [J]. Journal of Guidance, Control and Dynamics, 2014, 37(4):1-10.

[9] Oshman Y, Davidson P. Optimization of observer trajectories for bearings-only target localization [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 892-902.

[10] Fosbury A M, Crassidis J L. Optimal trajectory determination for increased relative navigation observability of air vehicles[C]. AIAA Guidance, Navigation and Control Conference, Hawaii, USA, August 18-21, 2008.

[11] Pi J, Bang H. Trajectory design for improving observability of angles-only relative navigation between two satellites [J]. Journal of Astronautical Sciences, 2014, 61(4): 391-412.

[12] Luo J, Gong B, Yuan J, et al. Angles-only relative navigation and closed-loop guidance for spacecraft proximity operations [J]. Acta Astronautica, 2016, 128 (6): 91-106.

[13] D’Amico S, Ardaens J S, Gaias G, et al. Noncooperative rendezvous using angles-only optical navigation: system design and flight results [J]. Journal of Guidance, Control and Dynamics, 2013, 36(6): 375-389.

[14] Ponda S, Kolacinski R, Frazzoli E. Trajectory optimization for target localization using small unmanned aerial vehicles[C]. AIAA Guidance, Navigation, and Control Conference, Chicago, USA, August 10-13, 2009.

[15] Stephen B, Lieven V. Convex optimization[M]. London: Cambridge University Press, 2004.

[16] Clohessy W H, Wiltshire R S. Terminal guidance system for satellite proximity operations using Tschauner-Hempel equations [J]. Journal of Astronautical Sciences, 1960, 27(9):653-678.

[17] Grzymisch J, Fichter W. Analytic optimal observability maneuvers for in-orbit bearings-only rendezvous [J]. Journal of Guidance, Control and Dynamics, 2014, 37 (5): 1658-1664.

[18] Marler R T, Arora J S. Survey of multi-objective optimization methods for engineering [J]. Structural and Multidisciplinary Optimization, 2004, 26(6): 369-395.

Closed-LoopOptimalGuidanceforMulti-ConstrainedRendezvouswithAngles-OnlyNavigation

LUO Jian-jun1,2, LV Dong-sheng1,2, GONG Bai-chun3,YIN Ze-yang1,2

(1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. Science and Technology on Aerospace Flight Dynamics Laboratory, Xi’an 710072, China;3. School of Astronautics,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

The closed-loop optimal guidance problem of the multi-objective and multi-constrained autonomous rendezvous with angles-only navigation is investigated in this paper. Firstly, considering the observability and robustness requirements, the performance indexes of the multi-objective optimization of the angles-only navigation and rendezvous guidance are established. On this basis, the objective function of the multi-objective and multi-constrained optimal rendezvous problem, and the solution method of the optimal guidance problem based on convex optimization are presented. Secondly, the framework and solution of the closed-loop angles-only navigation and guidance are proposed according to the “coupling” relationship between the navigation and guidance. Finally, the effect of the observability on the navigation and guidance performance is analyzed by simulation, and the effectiveness of the proposed method is verified.

Observability; Multiple constraints; Robustness; Convex optimization; Closed-loop guidance

V448

A

1000-1328(2017)09- 0956- 08

10.3873/j.issn.1000-1328.2017.09.008

2017- 04- 05;

2017- 06- 26

国家自然科学基金(61690210,61960211)

罗建军(1965-)，男，教授，主要从事航天飞行动力学、导航、制导与控制等方面的研究。

通信地址：陕西省西安市友谊西路127号(710072)

电话：(029)88493685

E-mail: jjluo@nwpu.edu.cn