低温推进剂复合材料贮箱基体开裂预测方法

任明法，张笑闻，常 鑫，黄 诚，王 博

(1. 大连理工大学工程力学系，大连 116024；2. 大连理工大学工业装备结构分析国家重点实验室,大连 116024；3. 北京宇航系统工程研究所，北京 100076)

低温推进剂复合材料贮箱基体开裂预测方法

任明法1,2，张笑闻1,2，常 鑫1,2，黄 诚3，王 博1,2

(1. 大连理工大学工程力学系，大连 116024；2. 大连理工大学工业装备结构分析国家重点实验室,大连 116024；3. 北京宇航系统工程研究所，北京 100076)

基于六边形单胞模型，构建了宏细观结构力学响应场间的关联矩阵，建立了低温推进剂复合材料贮箱结构的宏细观一体化分析方法，采用工程常用的能够预测不同失效模式的宏细观强度准则，对机械和温度载荷下复合材料层合板的基体开裂进行预测。结果表明：在机械载荷下，与试验数据相比，宏观Hashin准则、改进的宏观Tsai-Wu准则、细观最大应力准则和细观Hashin准则均具有良好的预测精度。但在温度载荷下，由于考虑了组分材料间热力学性能的不匹配，使用细观强度准则与宏观强度准则预测的结果相比具有一定差异。通过对不同载荷情况下基体开裂预测结果的分析，提出了采用细观最大应力准则作为基体开裂判据，同时结合考虑组分材料热力学性能差异影响的宏细观一体化分析方法，可以有效地对低温推进剂复合材料贮箱结构的基体开裂进行预测。

复合材料贮箱；基体开裂；低温；单胞模型；强度准则；宏细观一体化分析方法

0 引 言

低温推进剂贮箱作为航天运载器的核心组件，在推进系统中所占重量和体积的比例最大，是运载器结构中最主要的部件[1]。目前，全复合材料贮箱由于去除内衬结构，可以减轻约25%的质量[2]，对航天运载器的轻量化发展具有深远的战略意义[3]。但由于缺少了防止液体燃料泄漏的金属或聚合物内衬，其复合材料缠绕层还需兼具防止液体燃料泄漏的功能。而复合材料基体开裂是引起全复合材料贮箱中缠绕层形成泄漏通道的主要因素之一[2]，因此如何准确地预测低温环境下复合材料贮箱中的基体开裂，成为全复合材料贮箱结构设计和制造的关键问题之一。

基于材料强度理论预测复合材料贮箱结构基体开裂可采用两种方法，一是采用宏观力学分析方法，即以单层复合材料的宏观均匀性质表征材料性能，采用层合理论对复合材料结构的力学行为进行分析，并依据单层宏观尺度上的复合材料强度理论[4]，对复合材料中的基体开裂进行预测。二是采用宏细观一体化分析方法，即通过基于细观力学模型构建宏细观结构力学响应的分析模型，基体开裂准则可采用组分相材料层次，即细观尺度下的细观强度准则。采用细观力学准则的宏细观一体化分析方法将纤维和基体分别看作均匀材料，可以考虑纤维的几何形状和布置形式、纤维和基体的力学性能、纤维和基体之间的相互作用等的影响并可分析在加载过程中组分材料的损伤演化过程。其中，宏细观一体化分析方法的关键问题在于如何构建跨尺度力学响应场。

在采用宏细观一体化分析方法进行复合材料结构分析时，使用宏观强度准则和细观强度准则均可以对基体开裂失效模式进行判断。工程应用中往往采用能够区分不同失效模式的单层板尺度宏观强度准则对复合材料基体开裂进行判定，如：宏观Hashin准则[5]、改进的宏观Tsai-Wu准则[6]等，吴义韬等[7]较为全面的对宏观强度准则进行了总结和评述。总体上说，针对常温复合材料结构的分析，宏观强度准则能够获得比较准确预测结果。

目前，常用的细观强度准则有最大应力准则[8]、细观Mises准则[9]和细观Hashin准则[10]等，这类准则均通过建立组分材料应力/应变分量的失效判别式对相应失效模式进行判断。Mayes等[10]基于三角形单胞模型，采用细观Hashin准则对层合板单双轴拉伸载荷下纤维断裂和基体开裂载荷进行预测，与试验结果较为吻合。Ha等[9]建立了矩形单胞模型，采用细观最大应力准则和细观Mises准则分别对双轴拉伸载荷下纤维和基体失效模式进行判断，其对应力失效包络曲线的预测结果与试验结果较为一致。

由于宏观强度准则需要在宏观单层板强度性能基础上进行基体开裂判断，其强度准则是经验性的、唯象的。在低温复合材料贮箱研发阶段，由于考虑到介质的相容性以及温度的影响，需要不断对基体材料进行改性[11]，即意味着重新测量相应单层板的强度性能参数，需要花费大量的试验时间和成本。相比之下，采用细观强度准则，在预测过程中仅需试验测定组分材料的强度性能，极大地减少了试验工作量，并可在失效判定过程中考虑各组分材料的损伤状态对整体贮箱结构承载性能的影响。

贮箱工作时处于极低温环境中[12-13]，巨大的温差能够导致热膨胀系数相互不匹配的组分材料间产生不可忽略的内应力[14]，在对复合材料贮箱结构基体开裂进行预测时需考虑此影响。另外，即使在纯机械载荷下对复合材料结构进行基体开裂分析时，目前研究工作[9-10,14]中使用的单胞模型具有不同构造形式，且采用的细观强度准则各异，缺少系统的比较和讨论。

本文针对低温推进剂复合材料贮箱结构，基于六边形单胞细观有限元模型[14]，建立了宏细观结构力学跨尺度响应场间的关联矩阵，实现了复合材料贮箱结构的宏细观跨尺度力学行为分析。同时，采用工程常用的复合材料的宏细观强度准则：宏观Hashin准则、改进的宏观Tsai-Wu准则以及细观最大应力准则、细观Mises准则和细观Hashin准则，对复合材料层合板结构的基体开裂载荷进行预测，并与相应的试验数据进行对比分析，通过讨论组分相材料热膨胀系数不匹配产生的内应力在分析中的差异以及对基体开裂的影响，提出采用细观最大应力准则的宏细观一体化分析方法可以有效地对低温推进剂复合材料贮箱结构的基体开裂进行预测。

1 基于单胞模型的宏细观一体化分析方法

基于单胞模型的复合材料宏细观一体化分析方法可以对具有周期性细观结构的复合材料力学性能进行分析。分析示意图如图1所示，白色箭头表示力学响应量从贮箱结构的宏观尺度向细观尺度传递，黑色箭头表示材料性能由单胞模型逐渐传递至结构的宏观尺度。针对碳纤维增强环氧树脂基复合材料，六边形单胞具有更好横观各向同性性能[14]，本研究选择六边形单胞建立有限元模型。单胞几何模型采用贮箱常见的纤维体分比60%。

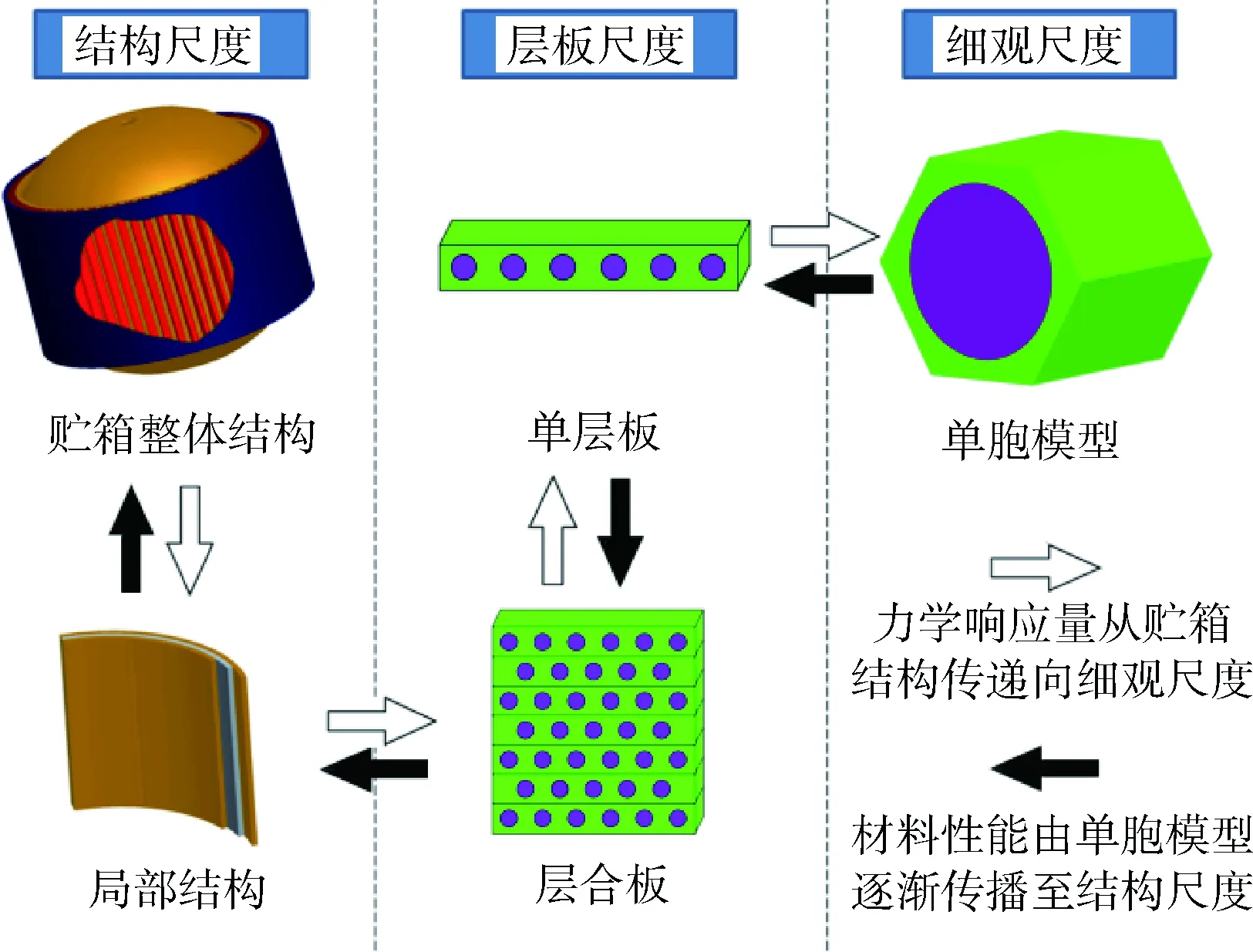
图1 碳纤维复合材料宏细观一体化分析示意图Fig.1 Illusion of integrated macro/micro analysis of graphite/epoxy composite structure

实施的流程：首先构建跨尺度响应场和尺度关联关系，再应用宏细观一体化分析流程实现求解，下面具体介绍宏细观一体化分析方法的实施过程。

1.1跨尺度响应场构建方法

假定复合材料为均匀的横观各向同性材料，其热力学本构方程可以表述为

(1)

首先，针对六边形单胞模型，不考虑温度变化，对模型边界施加单位宏观应变，同时施加相应的周期性位移边界条件并计算求得细观应力场，此时即可获取等效刚度矩阵C中的一列；重复上述步骤，即可获取完整的等效宏观刚度矩阵C，其中周期性位移边界条件见文献[14]。

其次，通过对单胞模型中的单元应力进行体积平均，可以获取等效宏观应力

(2)

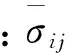
然后，对单胞模型整体施加温度载荷和周期性位移边界条件，结合式(1)即可获得下式

(3)

等效热膨胀系数矩阵α*

(4)

这样将材料性能由细观的单胞模型传递至宏观尺度，完成了宏观复合材料等效性能的获取。同时，在得到单位应变与单位温度载荷下的单胞细观应力场即单位细观应力场之后，通过宏观复合材料结构的有限元分析，得到单层板尺度的宏观应变，再结合之前所得的单位细观应力场，以宏观应变与温度载荷作为叠加系数对其进行叠加，得到单元或节点的细观应力场，并对细观应力场中基体单元的细观应力进行平均，进而完成了宏观结构响应向细观尺度的传递。叠加方法如下式所示

σ=Heε+SeΔT

(5)

式中：σ为单元或节点的细观应力；He为单胞受到各单位应变时的单位细观应力场；ε为单元或节点的宏观应变；Se为单胞受到单位温度载荷时的单位细观应力场。

最后，与Mayes的MCT方法类似[10]，对单胞模型中基体单元的细观应力进行平均，如式(6)所示

(6)

1.2宏细观一体化分析流程

使用宏细观一体化分析方法，获取单胞模型中基体单元中的平均细观应力，采用细观强度准则，实现复合材料贮箱结构基体开裂预测，分析流程如图2所示。

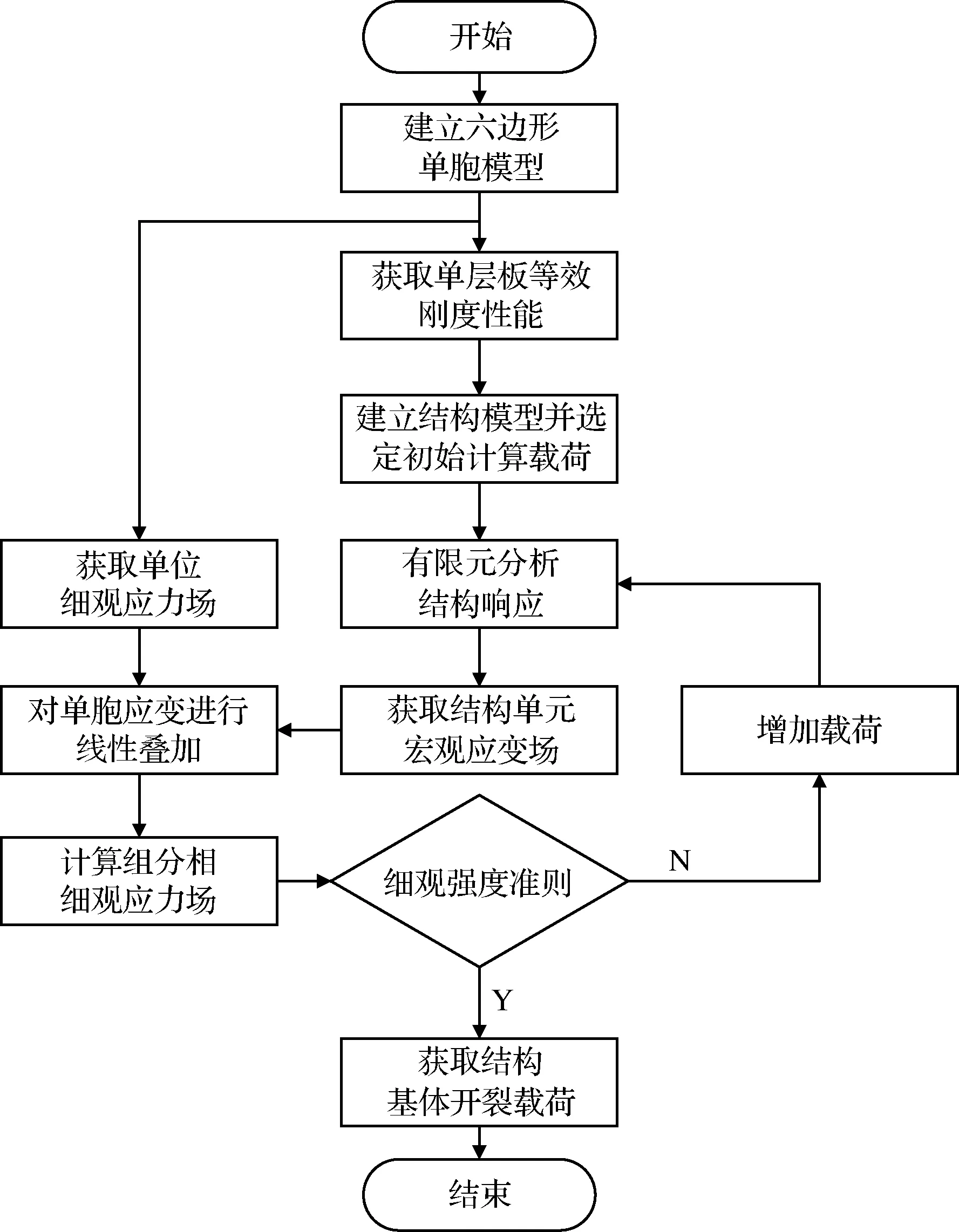
图2 复合材料贮箱结构的基体开裂预测分析流程图Fig.2 Flow chart of prediction and analysis for matrix cracking in composite tanks

首先，基于组分材料的热力学性能试验数据，选取六边形单胞模型并施加周期位移边界条件，通过细观有限元分析得到复合材料等效宏观热力学性能，以及各个单位应变及单位温度载荷下单胞模型的细观应力场。

然后，将得到的复合材料等效刚度性能作为输入数据，建立复合材料结构有限元模型，通过有限元分析得到宏观结构响应。

最后，以宏观结构中单元的宏观应变为线性叠加系数，叠加到第一步获得的细观应力场中，即可得到宏观单元在相应载荷下的细观应力场。获取组分材料的细观应力场后，在细观尺度下将基体单元的细观应力代入细观强度准则进行判定，从而判断基体是否发生破坏，不断重复这一过程直到某层中发生基体开裂，获取此时的载荷值作为复合材料贮箱结构基体开裂的预测值。

2 复合材料宏细观强度准则

2.1宏观强度准则

能区分失效模式的复合材料宏观强度准则中，宏观Hashin准则和改进的宏观Tsai-Wu准则表达形式简单且具有较高预测精度，其表达式如下：

1)宏观Hashin准则

当σ22+σ33>0时，基体拉伸开裂准则表达式为

(7)

当σ22+σ33≤0时，基体压缩开裂准则表达式为

(8)

式中：σij为单层板应力状态；+S22和-S22分别为单层板横向拉伸强度和横向压缩强度，S12和S23分别为单层板面内和出平面方向上的剪切强度。

2)改进的宏观Tsai-Wu准则

(9)

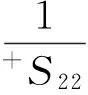
(10)式中：F2、F22、F12和F66为与复合材料单层板强度性能相关的强度参数。在基体开裂分析时，本文忽略纵横向正应力之间的耦合作用，即取的值为零。

2.2细观强度准则

常用的细观强度准则有细观最大应力准则、细观Mises准则以及细观Hashin准则，其表达式如下所示：

1)细观最大应力准则

(11)

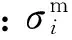
2)细观Mises准则

(12)

式中：I1m和σVM分别为基体材料的第一应力不变量与Von Mises应力。I1m和σVM表达形式为

(13)

σVM=

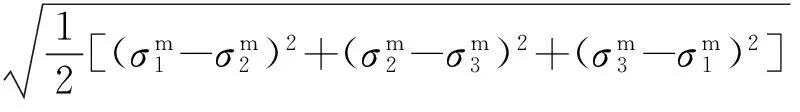
(14)

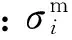
3)细观Hashin准则

(15)式中：Iim为基体材料的应力不变量；±K2m、K3m和K4m为与基体材料强度性能相关的强度参数，其表达式为

(16)

(17)

3 数值分析及讨论

3.1宏细观一体化分析方法验证

由于细观尺度下纤维和基体材料之间的应力场难以用试验测得，使用基于六边形单胞模型的复合材料宏细观一体化分析方法，针对AS4碳纤维材料和3501-6环氧树脂材料性能对单层复合材料刚度性能和横向强度进行预测，验证该方法的预测精度。

3.1.1 刚度性能

AS4/3501-6碳纤维增强复合材料组分材料性能如表1所示，通过细观力学有限元方法计算单胞模型中等效刚度矩阵C和等效热膨胀系数矩阵α*，获得复合材料单层板进行力学性能。

表1 AS4/3501-6复合材料组分材料刚度性能[10,15] Table 1 Stiffness properties of the constituent in AS4/3501-6 composite[10,15]

表2 AS4/3501-6复合材料刚度性能的本文预测结果与试验数据对比Table 2 Comparison of the stiffness properties in AS4/3501-6 composite obtained by micromechanics analysis and experiments

3.1.2 单层板横向拉伸强度

针对AS4/3501-6复合材料体系，结合宏细观一体化分析方法，采用3种细观强度准则对单层板横向拉伸强度进行预测，并与试验数据进行对比。其中，复合材料刚度性能如表2所示，树脂基体的强度参数如表3所示，对比结果如图3所示。

细观最大应力准则与细观Hashin准则预测结果相近，其误差分别为7.29%和9.79%，与试验结果[16]相比较为精确；而细观Mises准则具有-27.71%的误差，预测精度较低。因此，采用细观最大应力准则与细观Hashin准则的预测结果较为准确。

表3 3501-6树脂材料强度参数[10, 15] Table 3 Strength properties of 3501-6 resin[10, 15]

图3 不同细观强度准则对AS4/3501-6复合材料横向拉伸强度预测Fig.3 Predictions of transverse tension strength for AS4/3501-6 composites when using different microscopic criteria

3.2机械载荷下宏细观强度准则预测对比

贮箱结构仅承受均匀内压时，贮箱箱体中纵横向应力比为1∶2。因此，采用纵横载荷比为1∶2的双轴层合板拉伸模拟贮箱中复合材料典型受载情况。

复合材料双轴拉伸试验件的几何模型参考文献[17]建立，总长度为260 mm，宽度为30 mm，交叉部分倒角半径为5 mm；由双轴拉伸试验的ISO国际标准[18]可知，分析区域边长通常不多于宽度的0.8 倍，文中将分析区域的边长取值为24 mm。层合板铺设角度为[90/±45/0]s，每层厚度0.125 mm；材料体系采用AS4/3501-6碳纤维复合材料，纤维体分比为60%。

图4 双轴拉伸试验件示意图Fig.4 Illustration of biaxial tension coupon

建立有限元模型(如图4所示)，采用薄壳单元对几何模型进行整体划分，模型纵横方向从0 MPa开始分别逐渐施加1 MPa和2 MPa的载荷增量步，从而对模型整体进行有限元计算；并选取第2.1和第2.2节所述的2种宏观强度准则和3种细观强度准则，对分析区域中基体开裂载荷进行预测。其中，复合材料刚度性能如表2所示，强度参数如表3和表4所示。结合宏细观一体化分析方法，并采用不同的宏细观强度准则，基体开裂载荷预测结果如图5所示。

表4 AS4/3501-6复合材料强度参数[16]

由图5可以看出，在[90/±45/0]s层合板常温双轴拉伸载荷下，改进的宏观Tsai-Wu准则和宏观Hashin准则对基体开裂载荷的预测结果相同，均为125 MPa，与试验数据[15]相比误差为4.17%。细观最大应力准则和细观Hashin准则预测基体开裂载荷和试验数据结果相近，分别为125 MPa和127 MPa，误差为4.17%和5.83%；而细观Mises准则预测结果为78 MPa，表现为-35.00%的误差，精度较差。

图5 不同宏细观强度准则对AS4/3501-6复合材料[90/±45/0]s层合板双轴拉伸的基体开裂载荷预测Fig.5 Difference of matrix cracking loads in the [90/±45/0]s laminates of AS4/3501-6 composite under biaxial tension when using different macroscopic and microscopic criteria

3.3温度载荷下宏细观强度准则预测对比

选取双轴拉伸载荷下预测结果准确的4种宏细观强度准则，对AS4/3501-6碳纤维复合材料[90/±45/0]s层合板的基体开裂载荷进行预测。本文不考虑复合材料中组分相材料性能与温度变化的相关性，采用常温下的材料性能进行分析。基体开裂温差的预测结果如图6所示。

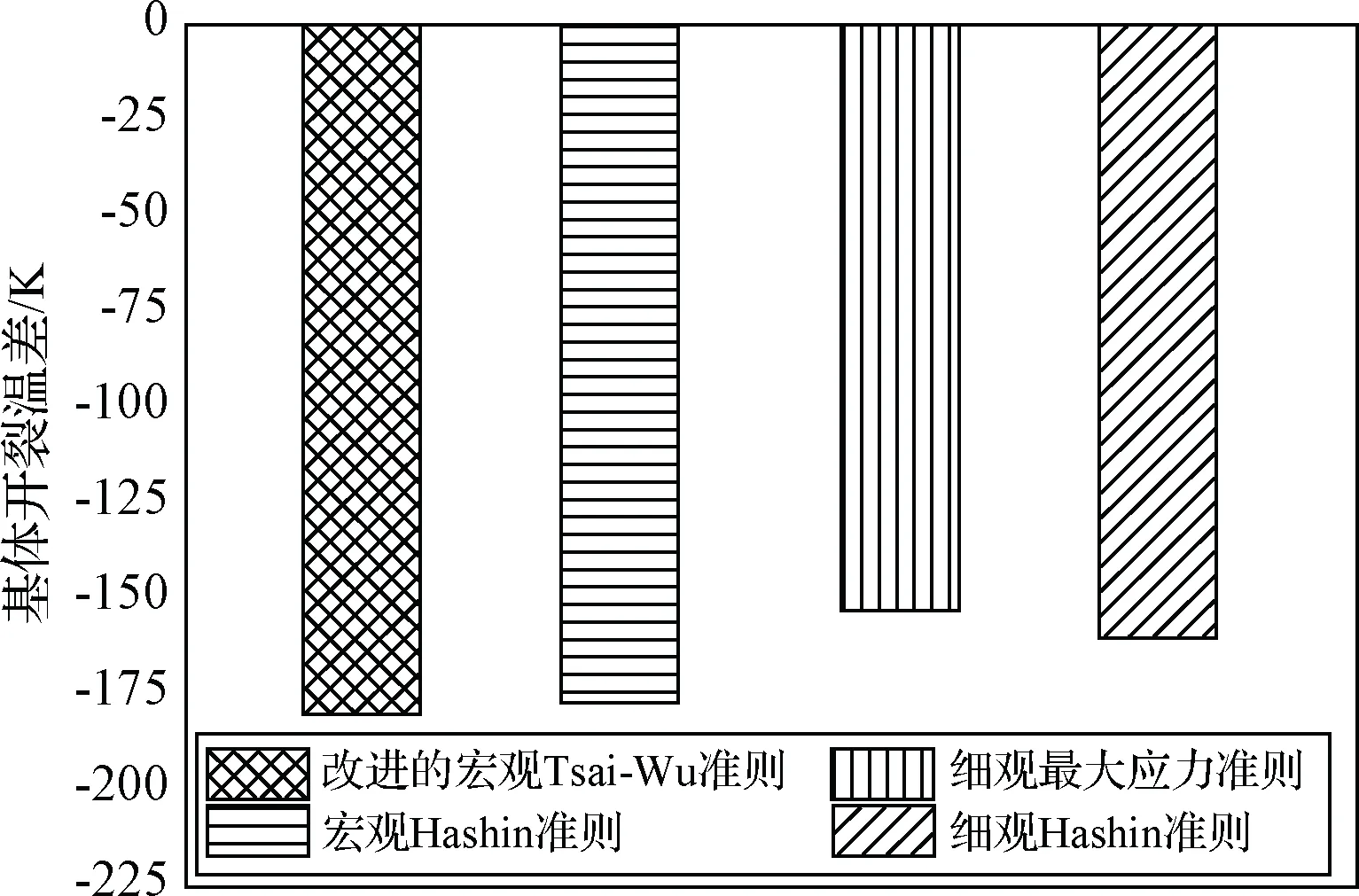
图6 不同宏细观强度准则对AS4/3501-6复合材料[90/±45/0]s层合板基体开裂温差的预测Fig.6 Temperature difference for initial matrix cracking of[90/±45/0]s laminates of AS4/3501-6 composite when using different macroscopic and microscopic criteria

由图6可知，在对层合板基体开裂温差的预测中，改进的宏观Tsai-Wu准则和宏观Hashin准则预测的层合板基体开裂温差分别为-180 K和-177 K；而细观最大应力准则预测结果为-153 K，细观Hashin准则预测结果为-160 K。

4种强度准则中，相同尺度的强度准则对基体开裂温差的预测结果差异不大，而宏细观强度准则的预测结果之间存在超过10%的差异。这是由于采用细观强度准则时，能够考虑复合材料中纤维材料与树脂基体之间的因热膨胀系数不同而产生的内应力对基体开裂的加剧作用。而采用宏观强度准则的宏观分析方法仅考虑了因复合材料层与层之间热膨胀系数不匹配所引起的宏观平均热应力，忽略了层内组分材料热膨胀系数之间不匹配性所引起的细观内应力。另外，相比于宏观强度准则，采用细观强度准则避免了单层板强度性能参数的测定，可节省试验成本。

细观最大应力准则和细观Hashin准则对基体开裂温差的预测结果相近，但最大应力准则的形式比细观Hashin准则简单，易于应用。同时，当复合材料在低温环境使用时，树脂材料由于内部分子链收缩而变脆，对于脆性且各向同性的树脂材料，使用最大应力准则对其拉伸破坏进行判断是合理的。

4 结 论

本文采用基于六边形单胞模型的宏细观一体化分析方法，通过单胞模型中细观应力场的线性叠加，建立了宏细观结构力学响应场间的关联矩阵，从而实现了宏观结构尺度与细观单胞尺度之间的跨尺度分析。同时，使用工程常用的宏细观强度准则，针对AS4/3501-6复合材料体系，对不同载荷下基体开裂载荷进行预测，并与试验数据进行对比，结果表明：

1)在单向拉伸载荷下，细观Mises准则预测误差为-27.7%，对基体开裂载荷预测精度较差，而使用细观最大应力准则和细观Hashin准则对基体开裂强度预测误差在10%以内，具有良好的预测精度。

2)在双轴拉伸载荷下，宏观Hashin准则、改进的宏观Tsai-Wu准则对层合板的基体开裂载荷预测误差在5%之内；细观最大应力准则、细观Hashin准则与试验数据相比误差在6%之内，均具有良好预测精度。

3)在温度载荷下，宏细观强度准则的预测结果之间存在超过10%的差异。采用复合材料的宏细观一体化分析方法和相应的细观最大应力准则作为基体开裂判据，可以有效地对低温推进剂复合材料贮箱结构的基体开裂进行预测。

[1] 黄诚, 雷勇军. 大型运载火箭低温复合材料贮箱设计研究进展[J]. 宇航材料工艺, 2015, 45(2):1-7. [Huang Cheng, Lei Yong-jun. Research progress on design of composite cryogenic [J]. Aerospace Materials & Technology, 2015, 45(2): 1-7.]

[2] Mallick K, Cronin J, Ryan K, et al. An integrated systematic approach to linerless composite tank development[C]. The 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Texas, USA, April 18-21, 2005.

[3] 梁辉, 孙雨果. 推进剂贮箱结构变厚度优化[J]. 宇航学报, 2007, 28(5):1349-1352. [Liang Hui, Sun Yu-guo. Variable thickness optimization of propellant tank structure [J]. Journal of Astronautics, 2007, 28(5):1349-1352.]

[4] Echaabi J, Trochu F, Gauvin R. Review of failure criteria of fibrous composite materials [J]. Polymer Composites, 1996, 17(6):786-798.

[5] Hashin Z. Failure criteria for unidirectional composites [J]. Journal of Applied Mechanics, 1980, 47(2): 329-334.

[6] Sun C T. Comparative evaluation of failure analysis methods for composite laminates [R]. Washington DC, USA: Office of Aviation Research, May 1996.

[7] 吴义韬, 姚卫星, 沈浩杰. 复合材料宏观强度准则预测能力分析[J]. 复合材料学报, 2015, 32(3): 864-873. [Wu Yi-tao, Yao Wei-xing, Shen Hao-jie. Prediction ability analysis of macroscopic strength criteria for composites [J]. Acta Materiae Compositae Sinica, 2015, 32(3): 864-873.]

[8] Boresi A P, Schmidt R J. Advanced mechanics of materials [M]. New York: John Wiley & Sons, 2005.

[9] Ha S K, Jin K K, Huang Y. Micro-mechanics of failure (MMF) for continuous fiber reinforced composites [J]. Journal of Composite Materials, 2008, 42(18): 1873-1895.

[10] Mayes J, Nickerson S, Welsh J. A multiscale approach to the effects of cryogenic environments on polymer matrix composites [C]. The 45th AIAA/ASME /ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, California, USA, April 19-22, 2004.

[11] 王君龙, 梁国正, 祝保林. 纳米SiO2对氰酸酯树脂的增韧改性研究[J]. 宇航学报, 2006, 27(4): 745-750. [Wang Jun-long, Liang Guo-zheng, Zhu Bao-lin. Research on modifying cyanate resin by nanometer silica[J]. Journal of Astronautics, 2006, 27(4): 745-750.]

[12] 马兴瑞, 于登云, 韩增尧, 等. 星箭力学环境分析与试验技术研究进展[J]. 宇航学报, 2006, 27(3): 323-331. [Ma Xing-rui, Yu Deng-yun, Han Zeng-yao, et al. Research evolution on the satellite-rocket mechanical environment analysis & test technology[J]. Journal of Astronautics, 2006, 27(3): 323-331.]

[13] 马兴瑞, 韩增尧, 邹元杰, 等. 航天器力学环境分析与条件设计研究进展[J]. 宇航学报, 2012, 33(1): 1-12. [Ma Xing-rui, Han Zeng-yao, Zou Yuan-jie, et al. Review and assessment of spacecraft mechanical environment analysis and specification determination [J]. Journal of Astronautics, 2012, 33(1): 1-12.]

[14] Huang C, Ren M F, Li T, et al. Trans-scale modeling framework for failure analysis of cryogenic composite tanks [J]. Composites Part B: Engineering, 2016, 85: 41-49.

[15] Mayes J S, Hansen A C. Composite laminate failure analysis using multi-continuum theory [J]. Composites Science & Technology, 2004, 64(3-4): 379-394.

[16] Soden P D, Hinton M J, Kaddour A S. Lamina properties, lay-up configurations and loading conditions for a range of fibre-reinforced composite laminates [J]. Composites Science & Technology, 1998, 58(7): 1011-1022.

[17] Mayes J S. Micromechanics based failure analysis of composite structural laminates [R]. West Bethesda, Maryland, USA: Survivability, Structures, and Materials Directorate Technical Report, September 1999.

[18] ISO-16842:2004(E), Metallic materials-sheet and strip-biaxial tensile testing method using a cruciform test piece [S].

AMethodforMatrixCrackingPredictioninCompositeCryogenicPropellantTanks

REN Ming-fa1,2, ZHANG Xiao-wen1,2, CHANG Xin1,2, HUANG Cheng3, WANG Bo1,2

(1. Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China; 2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China;3. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)

Based on the hexagon unit cell, the correlation matrices between the mechanical response fields of macro and micro structures are constructed, and an integrated macro/micro analysis method in composite cryogenic propellant tanks is established in this paper. With the commonly used engineering strength criteria capable of predicting the different damage modes, the matrix cracking in the composite laminate is predicted under the mechanical and temperature loads. Results show that the following criteria agree well with the test data under the mechanical loads, including the macroscopic Hashin criterion, modified macroscopic Tsai-Wu criterion, microscopic maximum stress criterion and microscopic Hashin criterion. However, considering the mismatching of the thermo-mechanical properties between the constituent materials, the predicted results using the microscopic strength criteria have imparities compared with the results using the macroscopic strength criteria under the thermal loads. Based on the comparison and analysis of the predicted results of the matrix cracking under different loads, the integrated macro/micro analysis method is proposed by utilizing the microscopic maximum stress criterion. Moreover, this method considers the effect of the imparities in the thermo-mechanical properties between the constituent materials, and is an effective way for the matrix cracking prediction of the composite tanks.

Composite tanks; Matrix cracking; Cryogenic; Unit cell; Strength criterion; Integrated Macro/Micro analysis method

TB33

A

1000 -1328(2017)09- 1005- 08

10.3873/j.issn.1000-1328.2017.09.014

2017- 05- 03;

2017- 06- 30

国家自然科学基金(11372058)；国家973计划(2014CB046506，2014CB049000)

任明法(1974-)，男，博士，副教授，主要从事复合材料结构力学方面的研究。

通信地址：辽宁省大连市大连理工大学工程力学系(116024)

电话：(0411)84709161

E-mail: renmf@dlut.edu.cn