基于非线性扰动观测器的四旋翼鲁棒编队控制

孙慧玉 宋光明 刘盛松 韦 中 张 勇 尤 剑

(1东南大学仪器科学与工程学院,南京210096)(2江苏电力公司电力调度控制中心,南京210029)

基于非线性扰动观测器的四旋翼鲁棒编队控制

孙慧玉1宋光明1刘盛松2韦 中1张 勇1尤 剑1

(1东南大学仪器科学与工程学院,南京210096)(2江苏电力公司电力调度控制中心,南京210029)

为了补偿四旋翼飞行器编队飞行过程中受到的模型不确定性和外部干扰,提出了一种分布式非线性扰动观测器(NDOB)．首先,考虑四旋翼模型不确定性和外部干扰,提出了一种新的四旋翼动力学模型．其次,在四旋翼飞行器的内部姿态回路中应用非线性扰动观测器,并且引入低通滤波器以滤除低频干扰．最后,引入风和不规则负载作为线性/非线性外部干扰,将NDOB控制器应用在领导-跟随的四旋翼编队中．仿真结果表明,在该观测器的作用下,扰动观测器能够完全抑制系统外部的线性风扰动,编队队形的整体偏移率在x和y轴上分别下降到0.01%和0.5%．对于非线性不规则负载运输实验,非线性扰动观测器对扰动的补偿率达到99.36%,能够有效地补偿四旋翼飞行器编队飞行过程中受到的模型不确定性和外部干扰．

四旋翼飞行器;非线性扰动观测器;编队飞行;鲁棒性分析

Abstract:A decentralized nonlinear disturbance observer (NDOB) was proposed for achieving a robust formation of UAVs subjected to the model uncertainties and external disturbances. Firstly, the dynamics model of the unmanned aerial vehicle (UAV), considering the model uncertainties and external disturbances was developed. Then, the NDOB controller was applied in the inner attitude loop of each UAV and a low pass filter was introduced to filter out the low frequency disturbances. Finally, the wind and the irregular loads were introduced as the linear and nonlinear external disturbances, applied to the leader-follower controlled formation of UAVs. The simulation results show that the disturbance observer can completely suppress the external linear wind disturbance and the overall offset of the formation can be reduced to 0.01% and 0.5% on the x and y axes, respectively. For the nonlinear irregular load transport experiment, the compensation rate of the disturbance is up to 99.36%, compensating for the model uncertainty and the external disturbance during the flight.

Keywords:unmanned aerial vehicle; nonlinear disturbance observer; formation flight; robustness analysis

近年来,多个无人机的协同编队飞行逐渐成为机器人领域的研究热点．多个结构简单的四旋翼组成的多机器人系统比单个结构功能复杂的四旋翼,具有成本低、鲁棒性和容错性好等优点．通过四旋翼的协作编队,可以完成大范围的侦测、大型或重型负载运输以及灾后搜救等任务[1-3]．

四旋翼协作编队任务中的关键问题是鲁棒编队飞行．在实际环境中,编队任务的成败主要取决于整个系统的鲁棒性．目前,编队飞行主要有多输入多输出法、领导-跟随法、虚拟结构法、基于行为法、无源控制法．但是,还没有文献直接表明这些编队方法本身可以抑制模型的不确定性和系统外部干扰．因此,许多学者致力于研究更加可靠和鲁棒的控制器以抑制模型不确定性和外部干扰．其代表性的研究成果为基于最优控制技术的Lyapunov鲁棒控制方法[4].文献[4]中使用状态反馈控制使得多个代理状态一致性成为可能．Wang等[5]提出了自适应鲁棒控制器,通过实验和模拟验证了自适应鲁棒控制器可以用来抑制系统外部干扰．Raffo等[6]提出的一种积分预测/非线性H∞控制器来解决四旋翼路径跟踪问题,在积分预测和非线性H∞两个控制器中,均考虑了位置误差的积分,当持续干扰作用于系统时,复合系统能够实现零稳态误差．上述控制器的主要特点是利用先进控制器来消除内部参数摄动和外部扰动对系统的影响．但是,先进控制器结构复杂,计算量大．近年来,扰动观测器引起了越来越多学者的关注和研究．扰动观测器是将外部力矩干扰及模型参数变化造成的实际对象与名义模型输出的差异等效到控制输入端，即在系统控制回路中引入等效补偿,从而实现对扰动的完全抑制的目的．而且,在引入扰动观测器的同时原来的系统控制结构不需要改变,传统的控制器可以按原来方案正常设计,从而降低了控制系统的复杂度．Xiong等[7]提出了基于非线性扰动观测器的控制器,用于在姿态控制中对单个四旋翼的外部干扰进行抑制．Dong等[8]提出了在单个四旋翼轨迹跟踪中采用基于扰动观测器的反演控制器,对系统负载变化、电机故障以及外部恒定风干扰进行观测和补偿．Lee等[9]提出了利用非线性扰动观测器补偿四旋翼系统姿态控制过程中的模型不确定性．

本文提出了一种分布式非线性扰动观测器,用于补偿四旋翼领导-跟随编队过程中受到的模型不确定和线性/非线性外部扰动的干扰．首先,考虑四旋翼模型的不确定性和外部干扰,提出新的四旋翼动力学模型．然后,根据新的四旋翼模型设计非线性扰动观测器模型，并且理论证明四旋翼编队拓扑结构的鲁棒性．最后,在仿真实验中,引入风和不规则负载作为线性/非线性外部扰动,将扰动观测器应用于四旋翼领导-跟随编队中，并验证其有效性．

1 四旋翼动力学模型

为了便于非线性扰动观测器的设计,首先建立包括模型不确定性和外部干扰的新四旋翼动力学模型．如图1所示,由欧拉-牛顿定理可得,原四旋翼的动力学模型为

(1)

式中,r=[x,y,z]T为四旋翼在惯性坐标系{E}中的位置;Θ=[φ,θ,ψ]T分别为横滚、俯仰以及偏航角;U1为四旋翼在机体坐标系{B}下所受的升力;U2,U3,U4分别为机体绕x，y，z轴的旋转力矩;Ix,Iy,Iz分别为x,y,z轴方向上的转动惯量;m为四旋翼的质量;g为重力加速度．

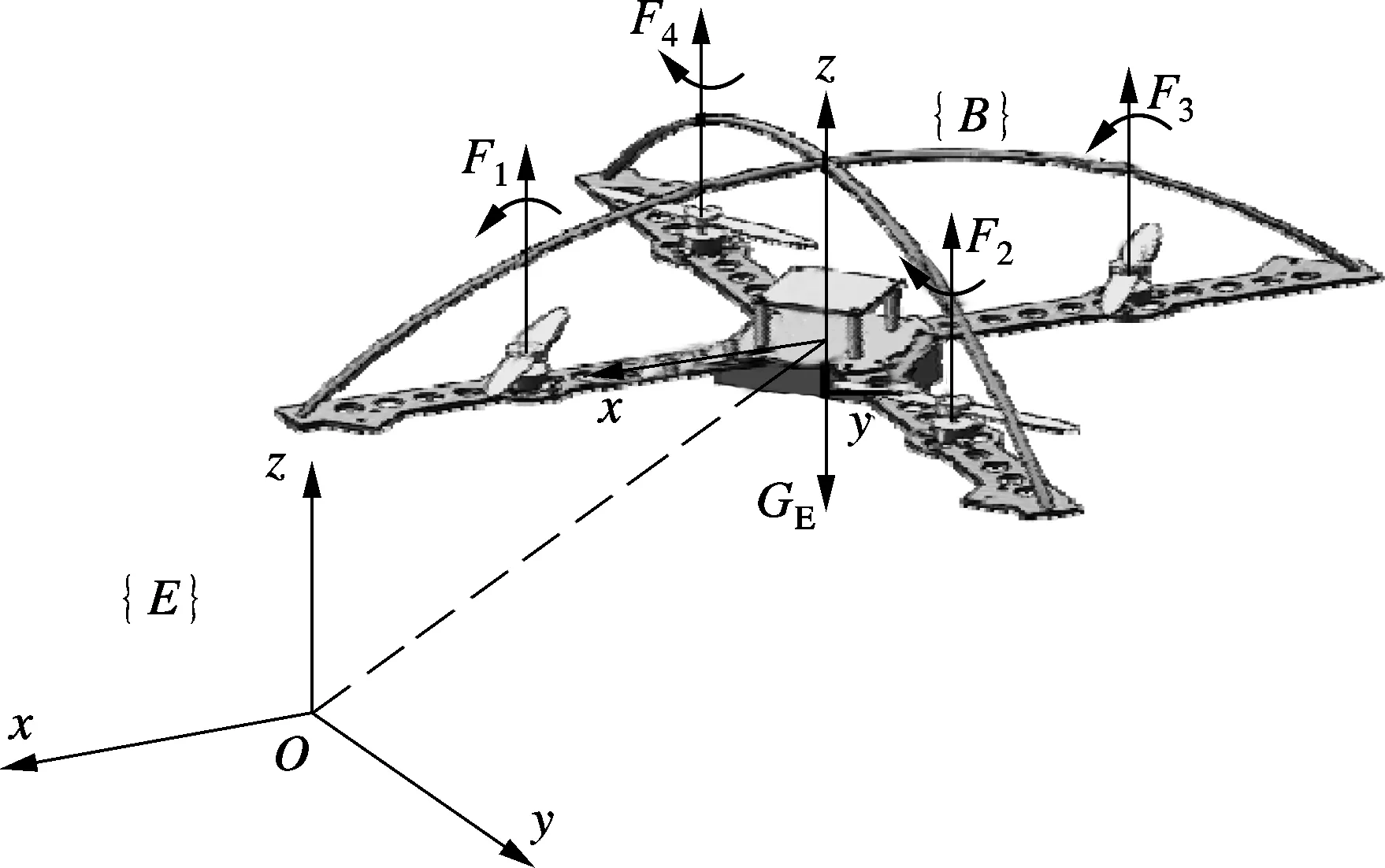
图1 四旋翼的动力学模型

四旋翼在机体坐标系{B}下的控制输入分别为

(2)

式中,Fi(i=1,2,3,4)为转子i产生的推力;Mi(i=1,2,3,4)为旋翼i的扭矩;l为旋翼中心到机体重心的距离．

考虑模型的不确定性和外部干扰,四旋翼的姿态子系统的动力学模型可重新建模为

(3)

式中,x=[x1,x2] 为状态变量,x1为四旋翼的位置或姿态角,x2为四旋翼的平移速度或角速度;u(t)为四旋翼姿态运动的控制输入;F(x),G(x),F0(x),G0(x)为可建模的非线性函数;ΔF(x),ΔG(x)为有界模型不确定性;d(x,t)为有界外部干扰的未知函数．

在动力学模型(1)中,姿态子系统重新建模为

(4)

根据式(3),姿态子系统中的状态变量x=[x1,x2]可设为

(5)

因此,非线性函数F0(x),G0(x)为

(6)

(7)

同时,四旋翼姿态运动的输入控制变量定义为

u=[U2,U3,U4]

(8)

2 非线性扰动观测器设计

2.1 控制器设计

如图2所示,在四旋翼内部环路中设计非线性扰动观测器,用于补偿模型的不确定性和外部干扰．非线性扰动观测器的设计如下．

图2 基于非线性扰动观测器的四旋翼串级控制框图

根据式(3),模型的不确定和外部干扰定义为总扰动,即

γ=d(x,t)+ΔF(x)+ΔG(x)u(t)=

(9)

结合式(9),非线性扰动观测器设计为

(10)

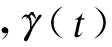
然而,在实际飞行测试中,四旋翼的角加速度信号难以获得．因此,只能利用四旋翼角速度信号,非线性扰动观测器重新设计为

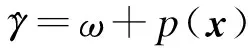
(11)

式中,ω2为中间变量;p(x)为关于变量x的非线性函数．

p(x)定义为

(12)

-JL(x)(ω+p(x)+F0(x)+G0(x)u(t))

(13)

JL(x)(ω+p(x)+F0(x)+G0(x)u(t))-JL(x)= JL(x)(ω+p(x))-JL(x)(-F0(x)+G0(x)u(t))=

(14)

故观测误差满足

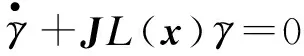
(15)

根据李雅谱诺夫稳定判据,非线性观测器的李雅谱诺夫函数可以定义为

(16)

非线性观测器全局渐进稳定,当L(x)满足

L(x)=J-1diag{a,a}a>0

(17)

同时,非线性函数p(x)为

p(x)=J-1ax

(18)

综上所述,非线性扰动观测器设计为

(19)

(20)

2.2 编队拓扑结构的鲁棒性分析

在有外部干扰的情况下,如果单个四旋翼能够通过干扰补偿无误差地跟踪指定轨迹,则四旋翼的编队拓扑在扰动环境下即可保持稳定．因此,受到外部干扰的编队拓扑结构的鲁棒性可以推导出单个四旋翼路径跟踪问题的稳定性．

首先,四旋翼位置控制如下:

(21)

(22)

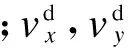
当四旋翼跌落撞击或翻转时,期望的俯仰和滚转角将无限地增加,此时外部干扰等效估计没有意义．为了避免这个缺陷,引入饱和边界函数

(23)

式中,φmax,θmax分别为最大俯仰角和横滚角．

根据式(21)路径跟踪的稳定性分析，可以得到四旋翼的速度有界性证明．四旋翼速度有界性分析如下:

Δv=v-vd

(24)

将式(22)代入式(24),可得

(25)

(26)

引理1[11]考虑状态空间中的线性时不变系统

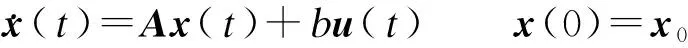
(27)

在有外部干扰的环境下,四旋翼编队拓扑结构的鲁棒性得到保证．

3 实验结果与讨论

在实验中,将风和不规则负载作为线性/非线性外部干扰．四旋翼领导-跟随编队飞行的模拟实验在MatlabR2010a/Simulink上进行．四旋翼模型的控制器参数如表1所示．头机 (简称L) 的初始位置为(xL(0),yL(0),zL(0))=(0,0,0) m,vL=0 m/s,wL=0 rad．从机1(简称F1) 的初始条件为(xF1(0),yF1(0),zF1(0))=(0,1,0) m,vF1=0 m/s,wF1=0 rad．从机2 (简称F2) 的初始条件为(xF2(0),yF2(0),zF2(0))=(0,-1,0) m,vF2=0 m/s,wF2=0 rad．领导-跟随编队的期望高度为3 m,相对距离为dLF1=dLF2=65 cm,相对方位为ΨLF1=0.75π,ΨLF2=±0.75π．

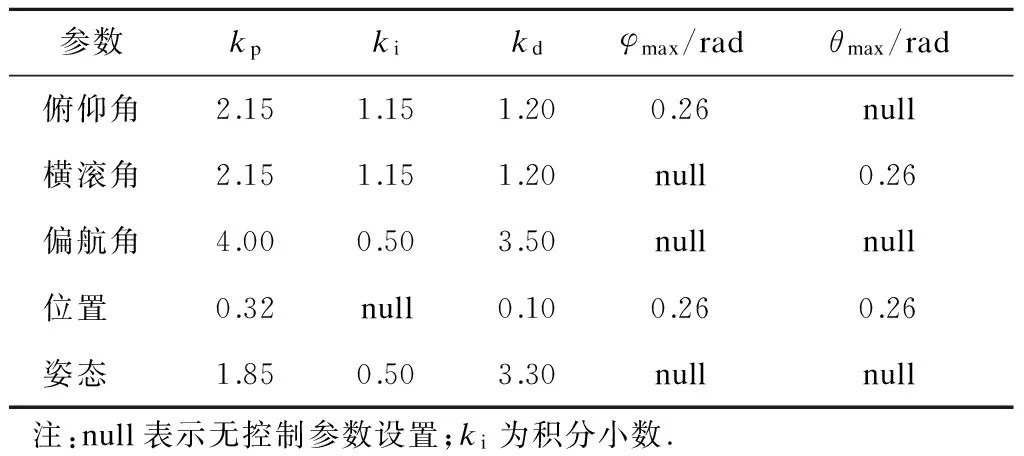
表1 四旋翼模型的控制参数

3.1 线性风扰动

在扰动测试前,首先进行风力测试．由电扇人为产生风,从而研究不同风速下风力的大小．风速由风速计(AR816)进行测量．风速/风力与四旋翼和电扇之间的距离关系如图3所示．

图3 风速/风力与四旋翼和电扇之间的距离关系图

在恒定风扰动实验中,施加到四旋翼编队上的风速为1.5 m/s,风力为Ux=Uy=0.86 N．首先,在没有非线性扰动观测器的补偿下,四旋翼在风中的领导-跟随编队如图4所示．在图中,编队每秒采样17次,编队总共持续90 s．在0～10 s期间,在没有风扰动的情况下,2个跟随四旋翼与领导者保持着期望的距离和方位．在第10秒时,风沿着x轴和y轴的斜对角线方向突然增加且一直持续到实验结束．由图4(a)看出,3个四旋翼沿着x，y对角线方向移动固定位移．编队的偏移率在x和y方向分别达到5.8%和10%．但是,编队仍保持着领导-跟随的编队队形,拓扑结构没有受到影响．

(a) 编队队形

(b) 编队队形偏移量

利用非线性扰动观测器补偿外部风扰动,四旋翼的编队队形如图5所示．由图5(a)可见,在非线性扰动观测器的作用下,控制器通过补偿外部风扰动使其编队队形得到校正．编队的偏移率在x和y方向分别降低到0.01%和0.5%．由图5(b)可见,力扰动的估计量仅有1 s的延迟且补偿率为100%．由图5(c)和(d)可见,在非线性扰动观测器的作用下,2个跟随四旋翼与领导者保持着期望的相对距离(dLF1=dLF2=65 cm)和相对方位(ψLF1=0.75π,ψLF2=-0.75π)．

(a) 编队队形

(b) 力信息

(c) 相对距离

(d) 相对角度

3.2 非线性不规则负载运输

在不规则重型或大型负载运输过程中,不均匀的负载分布将导致编队队形的破坏,进而直接导致负载运输失败．因此,每个四旋翼之间的高度不平衡需要补偿．不规则负载运输的示意图如6所示．图中,均匀分布但形状不规则的薄木板搭载在3个四旋翼上,用于负载运输．点A到点B或点C的距离即为编队期望的相对距离dLF1,dLF2．点A到点B或点C之间的相对角为编队期望的相对方位ψLF1,ψLF2．由于薄木板的形状不规则,通过悬挂法测量质量,重心从原来的点G1移动到点G2．实验中,0.724 kg的有效载荷完全附着于3个四旋翼上,不均匀负载分布分别为383,205和136 g,所受重力分别为3.753 4,2.009 0和1.332 8 N．非线性负载扰动应考虑空气动力学和噪声,即

Uz′=Uz+A′rands()

(28)

式中,Uz为z轴上编队所受的线性负载扰动量;A′为空气动力学扰动和噪声的总幅值;Uz′为z轴上编队受到的非线性负载扰动量．

图6 四旋翼编队中不规则负载运输示意图

不规则负载的编队飞行如图7所示．由图7(a)可见,在没有非线性扰动观测器的补偿下,载有不规则负荷的3个四旋翼飞行在不同的高度．由图7(b) 可见,当不规则的有效负载附着在四旋翼时,3个四旋翼的飞行高度出现不同的变化．领导-跟随编队队形被不均匀的载荷分布破坏,编队队形的破坏直接导致负载运输的失败．当直接将四旋翼姿态控制回路的积分项从0.5增加到5.1时,3个四旋翼的高度在10 s内显著上升到原始期望高度3 m．但是,从图7(c)可以看出,跟随四旋翼在高度上均有较大的振荡和超调,这也直接导致编队的失败．因而,直接调节四旋翼姿态子系统的控制参数不能抑制外部负载对编队的扰动．

利用非线性扰动观测器补偿非线性不规则负载的扰动,四旋翼的三维编队队形如图8(a)所示．在非线性扰动观测器的作用下,编队的刚性拓扑结构能够保持在相同的高度,如图8(b)所示．3个四旋翼能够迅速从0.4,1.6和2.2 m收敛至期望的编队高度3 m．非线性扰动观测器可以完全补偿由最大负载430 g产生的外力干扰,最大负载约为机体自身总重量360 g的1.2倍．在图8(c)中,由非线性扰动观测器预估的扰动力,包括非线性空气动力学干扰和噪声,其均值分别为3.729 3,1.996 1,1.324 3 N,其补偿率达到99.36%．由文献[5,8,12]可知,在工程实践中干扰观测器对外部风干扰和负载扰动的补偿率均达到90%．本文提出的分布式非线性扰动观测器在仿真实验中几乎能够完全补偿非线性不规则负载变化干扰,使得四旋翼编队系统能够满足运输不规则负载的要求,同时为工程验证提供了可能性．

(a) 编队队形

(b) 高度

(c) 提高姿态子系统积分系数后的高度 (ki=5.1)

(a) 编队队形

(b) 高度

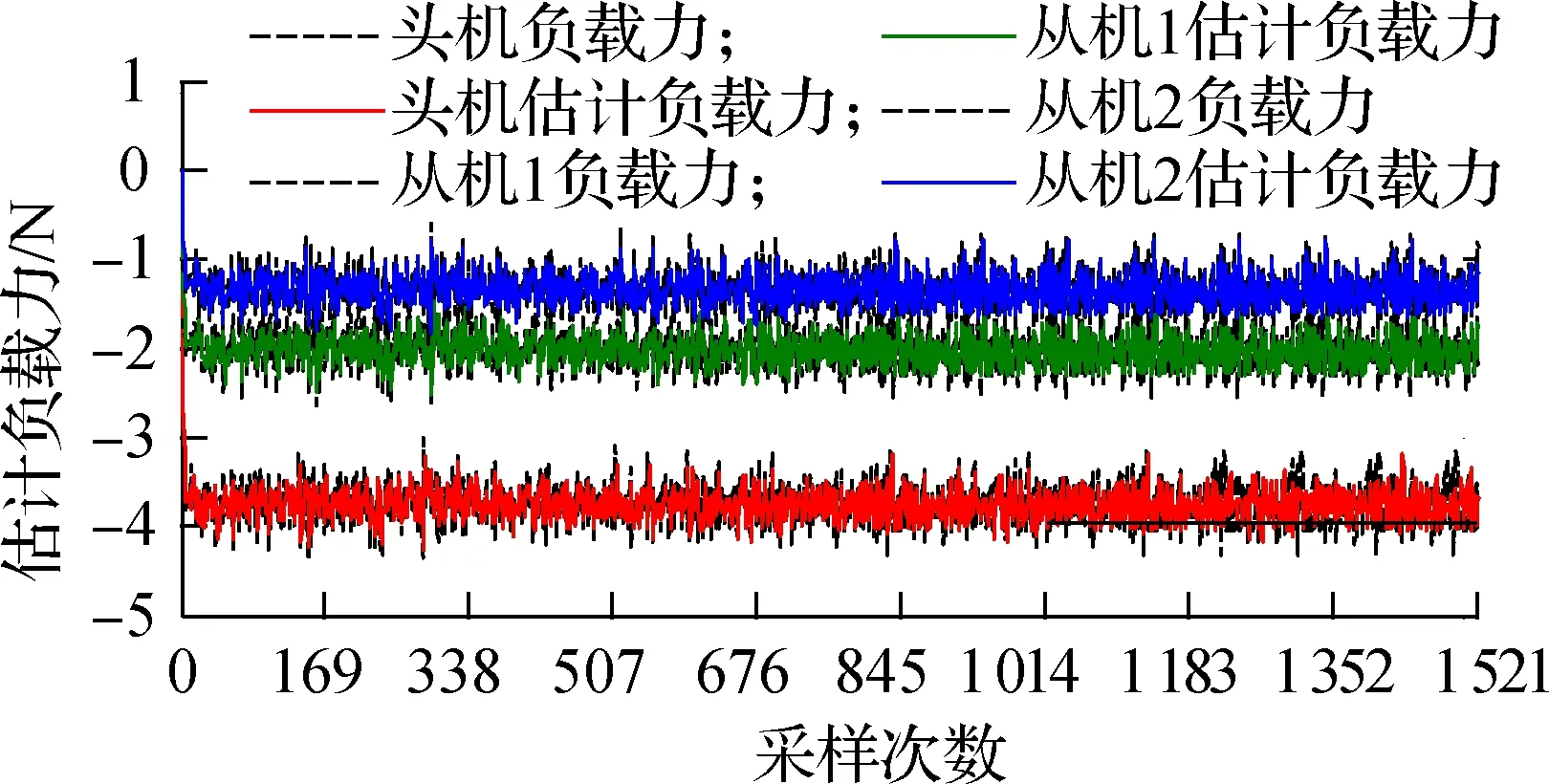
(c) 力信息

综上所述,本文提出的分布式非线性扰动观测器一方面能够独立于领导-跟随编队控制策略，并且不影响四旋翼的底层控制结构,观测器结构简单易实现,降低了系统的复杂度．另一方面,相比于其他控制器,观测器能够更加快速有效地抑制四旋翼编队系统的内部模型不确定性,同时补偿线性和非线性的外部扰动．分布式非线性扰动观测器与其他控制器的对比结果如表2所示．

表2 控制器效果对比

4 结论

1) 考虑四旋翼模型不确定性和外部干扰,提出了一种新的四旋翼动力学模型．

2) 在四旋翼内环姿态回路中,利用角速度信号设计非线性扰动观测器，且从理论上证明四旋翼编队拓扑结构的鲁棒性．

3) 仿真实验测试了包括风和非线性不规则负载2种不同的外部扰动．在风扰动实验中,采用非线性扰动观测器补偿恒定风扰动,编队队形的整体偏移率在x和y轴上分别降低到0.01%和0.5%．扰动观测器能够完全抑制系统外部的线性风扰动．对于非线性不规则负载运输实验,考虑非线性空气动力学干扰和噪声,非线性扰动观测器对扰动的补偿率达到99.36%,能够满足编队运输不规则负载的要求．

References)

[1] Crommelinck S, Bennett R, Gerke M, et al. Review of automatic feature extraction from high-resolution optical sensor data for UAV-based cadastral mapping[J].RemoteSensing, 2016,8(8): 689-717.

[2] Palunko I, Cruz P, Fierro R. Agile load transportation: Safe and efficient load manipulation with aerial robots [J].IEEERobotics&AutomationMagazine, 2012,19(3): 69-79. DOI:10.1109/mra.2012.2205617.

[3] Tomic T, Schmid K, Lutz P, et al. Toward a fully autonomous UAV: Research platform for indoor and outdoor urban search and rescue [J].IEEERobotics&AutomationMagazine, 2012,19(3): 46-56. DOI:10.1109/mra.2012.2206473.

[4] Cabecinhas D, Cunha R, Silvestre C. A nonlinear UAV trajectory tracking controller with disturbance rejection[J].ControlEngineeringPractice, 2014,26: 1-10. DOI:10.1109/acc.2014.6858615.

[5] Wang C, Song B, Huang P, et al. Trajectory tracking control for quadrotor robot subject to payload variation and wind gust disturbance[J].JournalofIntelligentandRoboticSystems, 2016,83(2): 315-333. DOI:10.1007/s10846-016-0333-4.

[6] Raffo G V, Ortega M G, Rubio F R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter[J].Automatica, 2010,46(1): 29-39.

[7] Xiong J J, Zheng E H. Position and attitude tracking control for a quadrotor UAV[J].ISATransactions, 2014,53(3): 725-731. DOI:10.1016/j.isatra.2014.01.004.

[8] Dong W, Gu G Y, Zhu X, et al. High-performance trajectory tracking control of a quadrotor with disturbance observer[J].SensorsandActuatorsA:Physical, 2014,211: 67-77. DOI:10.1016/j.sna.2014.03.011.

[9] Lee K, Back J, Choy I. Nonlinear disturbance observer based robust attitude tracking controller for quadrotor UAVs[J].InternationalJournalofControl,Automation,andSystems, 2014,12(6):1266-1275.DOI:10.1007/s12555-014-0145-x.

[10] Yang Z J, Tsubakihara H, Kanae S, et al. A novel robust nonlinear motion controller with disturbance observer[J].IEEETransactionsonControlSystemsTechnology, 2008,16(1): 137-147.

[11] Sun T, Liu F, Pei H, et al. Observer-based adaptive leader-following formation control for non-holonomic mobile robots[J].IETControlTheory&Applications, 2012,6(18):2835-2841. DOI:10.1049/iet-cta.2011.0492.

[12] Liu C, Chen W H, Andrews J. Tracking control of small-scale helicopters using explicit nonlinear MPC augmented with disturbance observers[J].ControlEngineeringPractice, 2012,20(3): 258-268. DOI:10.1016/j.conengprac.2011.10.015.

RobustformationcontrolofUAVsbasedonnonlineardisturbanceobserver

Sun Huiyu1Song Guangming1Liu Shengsong2Wei Zhong1Zhang Yong1You Jian1

(1School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China) (2Electric Power Dispatching and Control Center, Jiangsu Electric Power Company, Nanjing 210029, China)

TP249

A

1001-0505(2017)05-0926-07

2017-02-27.

孙慧玉(1989—), 女, 博士生; 宋光明(联系人), 男, 博士, 教授, 博士生导师, mikesong@seu.edu.cn.

国家自然科学基金资助项目(61375076)、江苏省普通高校研究生科研创新计划资助项目(KYLX16_0192).

孙慧玉，宋光明，刘盛松，等.基于非线性扰动观测器的四旋翼鲁棒编队控制[J].东南大学学报(自然科学版),2017,47(5):926-932.

10.3969/j.issn.1001-0505.2017.05.014.

10.3969/j.issn.1001-0505.2017.05.014