复杂分区域复合粗糙面的布儒斯特效应

邹高翔 童创明,2 孙华龙 彭 鹏,3 王 童

(1空军工程大学防空反导学院, 西安 710051)(2东南大学毫米波国家重点实验室, 南京 210096)(3西安电子科技大学物理与光电工程学院, 西安 710071)

复杂分区域复合粗糙面的布儒斯特效应

邹高翔1童创明1,2孙华龙1彭 鹏1,3王 童1

(1空军工程大学防空反导学院, 西安 710051)(2东南大学毫米波国家重点实验室, 南京 210096)(3西安电子科技大学物理与光电工程学院, 西安 710071)

为了研究复杂地表环境布儒斯特效应随环境参数的演变规律,通过分区域复合粗糙面建模方法,构建了多种复杂地表的粗糙面模型,并采用基于复杂分区域面元的自适应迭代物理光学法,研究了多种复杂分区域复合粗糙面的布儒斯特效应．结果表明,环境表面的介电常数和粗糙度是决定布儒斯特角位置的重要因素,不同介电常数所对应的布儒斯特角位置不同,均方根高度的增加会导致布儒斯特角的增大,而相关长度的增加会引起布儒斯特角的减小．在分区域复合粗糙面中,区域介电常数和区域粗糙度的改变均会引起布儒斯特角发生偏移的布儒斯特融合效应,且介电常数占优的区域粗糙度改变所引起的布儒斯特融合效应会更为显著．因此,对于复杂地表环境,在已知各区域表面介质常数与粗糙度的情况下,考虑布儒斯特融合效应即可确定该环境的布儒斯特角,为复杂环境下的超低空目标探测提供可靠的理论支撑．

分区域复合粗糙面;自适应迭代物理光学法;布儒斯特效应;介电常数;粗糙度

Abstract: To study the evolution rule of the Brewster effect with the parameters in complicated ground circumstance, the geometrical models of composite rough surfaces with diverse structures are established based on the composite rough surface modeling theory. And the Brewster effects of diverse composite rough surfaces are researched using an adaptive iterative physical optics based on facets of complicated composite rough surfaces. The results show that the dielectric constant and the roughness are significant factors which determine the position of the Brewster angle. The positions of the Brewter angles for different dielectric constants are distinct. The Brewster angle increases with the increase of the root mean square height while it decreases with the increase of the correlation length. Both the change of the regional dielectric constant and that of the regional roughness can lead to the deviation of the Brewster angle which is defined as the Brewster fusion effect, meanwhile the Brewster fusion effect is more remarkable induced by variance of roughness in rough surface region whose dielectric constant is dominant. Therefore, when the dielectric constant and the roughness of the complicated ground circumstance are known, the Brewster angle can be determined by considering the Brewster fusion effect, which can provide a reliable theoretical basis for the detection of super-low altitude targets in the complicated circumstances.

Keywords: composite rough surface; adaptive iterative physical optics; Brewster effect; dielectric constant; roughness

近年来,随机粗糙面的电磁散射研究备受关注[1-2]．在已有的粗糙面建模理论中,高斯谱[3]、指数谱[4]和PM谱[5]等谱函数常被学者们广泛应用于粗糙面的几何模型构建,它们能够反映出特有的统计规律,适合单一类型粗糙面的模拟．然而,自然环境表面通常具备复合性、多介质属性和多统计特性,这类复杂粗糙面的相关散射特性[6-9]成为近年来研究的热点之一．

国外学者已对布儒斯特效应进行了大量研究．文献[10-11]对一维、二维粗糙面的布儒斯特效应进行了详细分析;文献[12]研究了海面相关参数对海面布儒斯特效应的影响;文献[13]通过实验测量出布儒斯特角,并得到介质表面的介电常数．国内关于布儒斯特效应的研究较少．文献[14]结合四路径方法提出了广义布儒斯特效应,以对抗多径干扰;文献[9]对地海交界环境所存在的布儒斯特效应进行了探索．然而,目前关于多介质、多粗糙度环境布儒斯特效应的研究还比较少见．

区别于以往的随机表面建模理论,本课题组曾对分区域复合粗糙面的建模理论[6-9]进行了探索．在此基础上,本文提出了多种复杂分区域复合粗糙面建模方法,并采用自适应迭代物理光学法(AIPO)来分析其布儒斯特效应,探究了复杂分区域复合环境布儒斯特效应的内在规律．

1 理论分析

1.1 复杂分区域复合粗糙面建模

[6-9]中所提出的分区域复合粗糙面建模理论,对复杂分区域复合粗糙面进行建模．采用高斯谱函数作为生成粗糙面的基本函数,其统计特性可由均方根高度hrms和相关长度lx,ly来描述．

实现具备多重粗糙度的粗糙面,必须采用多种统计特性的谱函数进行线性滤波和逆傅里叶变换,然后采用反正切函数作为权函数,对其进行调制和区域间的平滑衔接．双重、三重和多重粗糙度分区域复合粗糙面的加权反正切函数表达式为

Fcom(x,y)=Fsur1(x,y)[π/2+arctan(y-y0)]/π+
Fsur2(x,y)[π/2-arctan(y-y0)]/π

(1)

Fcom(x,y)=Fsur1(x,y)[π/2+arctan(y-y1)]/π+

Fsur2(x,y)[π/2-arctan(y-y1)][π/2+arctan(y-

y2)]/π2+Fsur3(x,y)[π/2-arctan(y-y2)]/π

(2)

Fcom(x,y)=Fsur1(x,y)[π/2+arctan(y)][π/2+
arctan(x)]/π2+Fsur2(x,y)[π/2+arctan(y)][π/2-
arctan(x)]/π2+Fsur3(x,y)[π/2-arctan(y)][π/2+
arctan(x)]/π2+Fsur4(x,y)[π/2-arctan(y)][π/2-
arctan(x)]/π2

(3)

式中,Fcom(x,y)为分区域复合粗糙面在坐标(x,y)处的高度;Fsur1(x,y),Fsur2(x,y),Fsur3(x,y)和Fsur4(x,y)分别为单一粗糙面sur1,sur2,sur3,sur4在坐标(x,y)处的高度;y0为双重粗糙度分区域复合粗糙面的分界线(见图1(a));y1,y2为表示三重粗糙度分区域复合粗糙面的分界线(见图1(b)),可以根据实际需要进行调整,分界线也可以取x方向．通过设置各区域的hrms,lx,ly,经过加权反正切函数处理,得到3种多重粗糙度分区域复合粗糙面几何模型示意图(见图1)．

(a) 双重粗糙度

(c) 多重粗糙度

1.2 基于分区域面元的自适应迭代物理光学法

由复杂分区域复合粗糙面的建模可以得到,所分析的粗糙面模型可以包含多种介质以及粗糙度,这使得其介质成分变得更加复杂．某一区域表面介质的复折射率不一定满足阻抗边界条件,因此需要对原算法进行修正,同时采用电流、磁流进行迭代,对其散射进行求解．

迭代物理光学法以Stratton-Chu公式为基础,其表面电场积分方程和磁场积分方程主值形式为

(4)

(5)

(6)

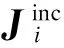
(7)

(8)

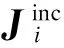
(9)

J=Jinc+CM(J,M)

(10)

M=Minc+CE(J,M)

(11)

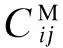
DJ(k+1)=Jinc+(UCM+LCM)J(k)k=0,1,2…

(12)

DM(k+1)=Minc+(UCE+LCE)M(k)k=0,1,2…

(13)

传统IPO算法通常设置一个固定的迭代次数,如果该迭代次数太小,则求解的精度可能不会满足要求[16]．因此,本文定义粗糙表面所有面元上的电流能量和磁流能量如下:

(14)

(15)

(16)

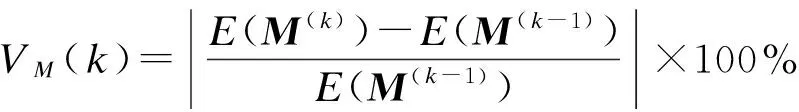
(17)

式中,J(k-1),M(k-1)分别为第k-1次的感应电流和感应磁流．通过上述定义,当改变速率VJ,VM小于设定值(通常取3%～5%[16])时停止迭代,即可得到最终的粗糙表面电磁流分布．将结果代入式(4)和(5),便可获得粗糙表面的电磁散射．为保证计算精度,本文算例中均建立50个几何模型样本,计算得到散射系数的集平均值,以此作为仿真结果．

1.3AIPO算法验证

工作频率f=1 GHz,粗糙面选取为高斯谱粗糙面,其电尺寸为30λ×30λ,其中λ为对应的波长;统计参数为均方根高度hrms=0.4λ,相关长度l=lx=ly=1.0λ,介电常数为εr=(30.0,-3.6j),该条件下表面曲率半径ρ=9 526λ,不满足基尔霍夫近似条件．在锥形波照射下,设置入射角θi和入射方位角φi分别为60°和0°;设置散射角θs为-90°～90°,散射方位角φs与φi相同．仿真计算机的配置如下:主频2.6 GHz,内存4 GB．将AIPO算法的双站散射系数[9]数值结果与基于矩量法的MLFMM算法以及PO算法的计算结果进行比较,结果见图2.

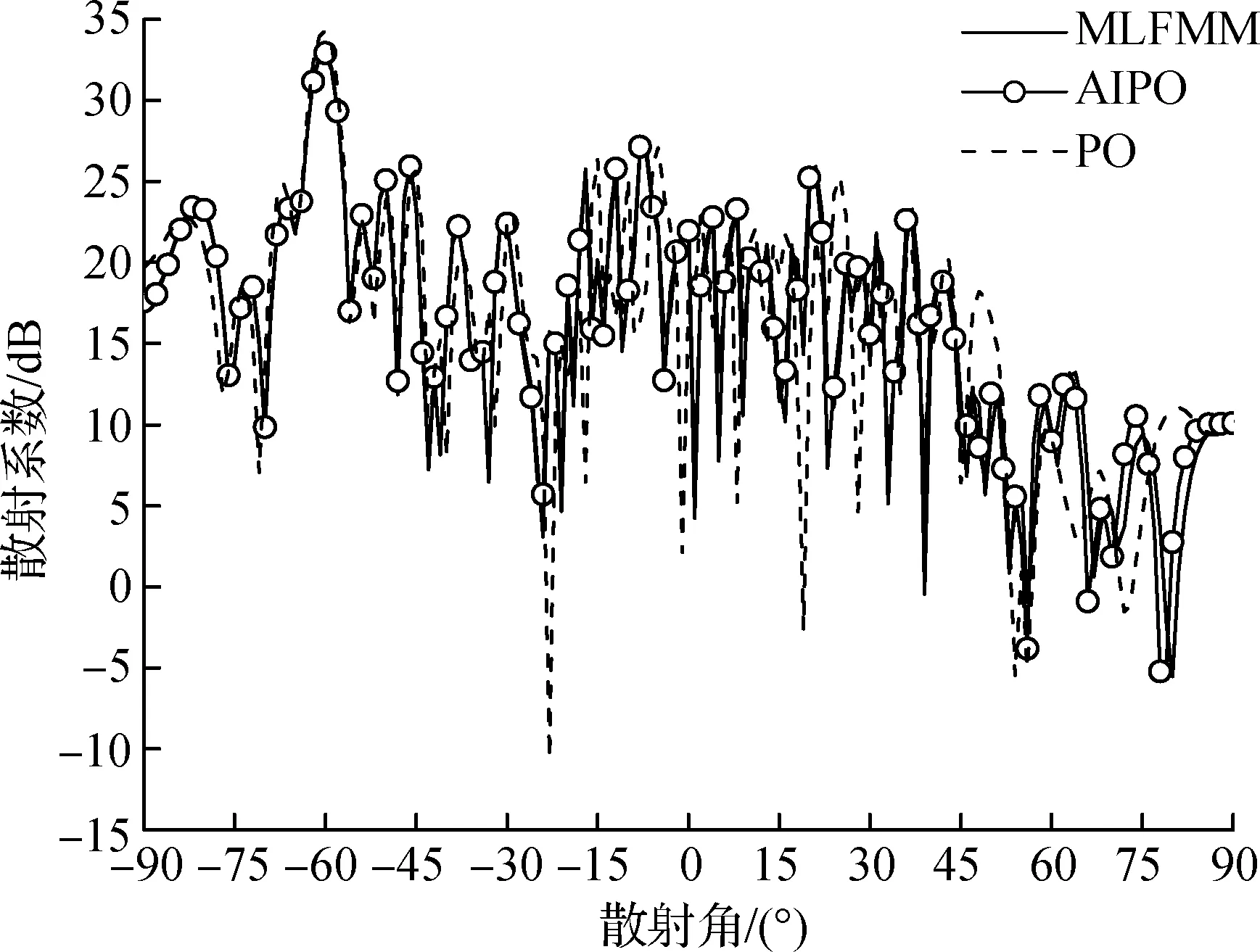
(a) HH极化

(b) VV极化

由图2可知,在HH极化和VV极化条件下,AIPO算法与MLFMM算法的计算结果吻合较好,而PO算法则在各个散射角度上存在差异,尤其是大散射角范围．平均偏差和最大偏差分别为

(18)

(19)

式中,γT(θs)为AIPO算法或PO算法计算得到的散射系数;γMLFMM(θs)为MLFMM算法计算得到的散射系数;Nθs为散射角个数．

计算结果见表1．由表可得,PO算法与MLFMM算法所得结果差异较大,AIPO算法与MLFMM算法所得结果差异较小,从而证明了AIPO算法的有效性．同时,在HH极化和VV极化条件下,对于单次样本AIPO算法耗时分别为127和132 s,而MLFMM算法分别耗时682和693 s,由此可见,AIPO算法的运算效率明显提高．

表1 误差分析

2 布儒斯特效应仿真分析

2.1 不同介质的单粗糙度粗糙面

电磁波以垂直极化形式在特定角度照射介质表面,出现镜向散射为极小值的现象,即为布儒斯特效应．本文考察粗糙面的布儒斯特效应问题,故所选算例仅考虑垂直极化的情况．为与复杂分区域复合粗糙面进行对比,对不同介质的单一粗糙度粗糙面的布儒斯特效应进行仿真．在本节的所有算例中,若不做特殊说明,工作频率均设置为f=1 GHz,粗糙面的电尺寸设置为30λ×30λ,计算对象均为入射角θi为0°～90°,入射方位角φi为0°所对应的镜向散射系数．参照国际无线电咨询委员会推荐的一套地面反射系数图表,获得不同反射面的复介电常数．

粗糙面统计参数设置为hrms=0.1λ,0.3λ,l=lx=ly=1.0λ,根据表2所示不同反射面的复介电常数,采用AIPO算法进行计算,结果见图3．

表2 不同反射面的复介电常数

由图3可知,不同介质的随机粗糙表面均存在布儒斯特效应．当粗糙面的hrms由0.1λ增加到0.3λ时,混凝土表面的布儒斯特角(即擦地角)φB由31.5°变为38°,干地面表面的φB由28°变为35°,半干地面表面的φB由22.5°变为30°,湿地表面的φB由13°变为21.5°．由此得到,均方根高度hrms的增加会导致粗糙面φB的增大．

粗糙面统计参数设置为hrms=0.1λ,l=lx=ly=1.0λ,3.0λ,根据表2所示不同反射面的复介电常数,采用AIPO算法计算得到的仿真结果见图4．

由图4可知,当粗糙面的相关长度l由1.0λ增加到3.0λ时,混凝土表面的φB由31.5°变为30°,干地面表面的φB由28°变为26.5°,半干地面表面的φB由22.5°变为20.5°,湿地表面的φB由13°变为10.5°．由此得到,相关长度l的增加会导致粗糙面φB的减小．

(a) 混凝土表面

(b) 干地表面

(c) 半干地面表面

(d) 湿地表面

2.2 双介质双重粗糙度分区域复合粗糙面

设置表面sur1,sur2的统计参数相同,考察双介质分区域复合粗糙面的布儒斯特效应,仿真结果如图5所示．

(a) 混凝土表面

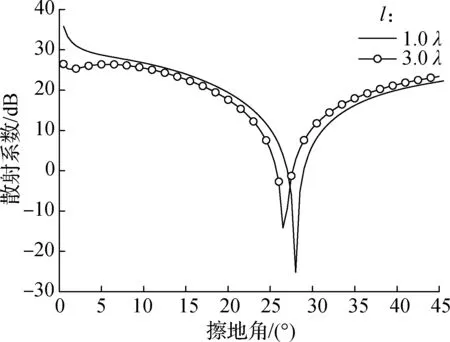
(b) 干地表面

(c) 半干地面表面

(d) 湿地表面

(a) hrms=0.1λ, lx=ly=1.0λ

(b) hrms=0.3λ, lx=ly=1.0λ

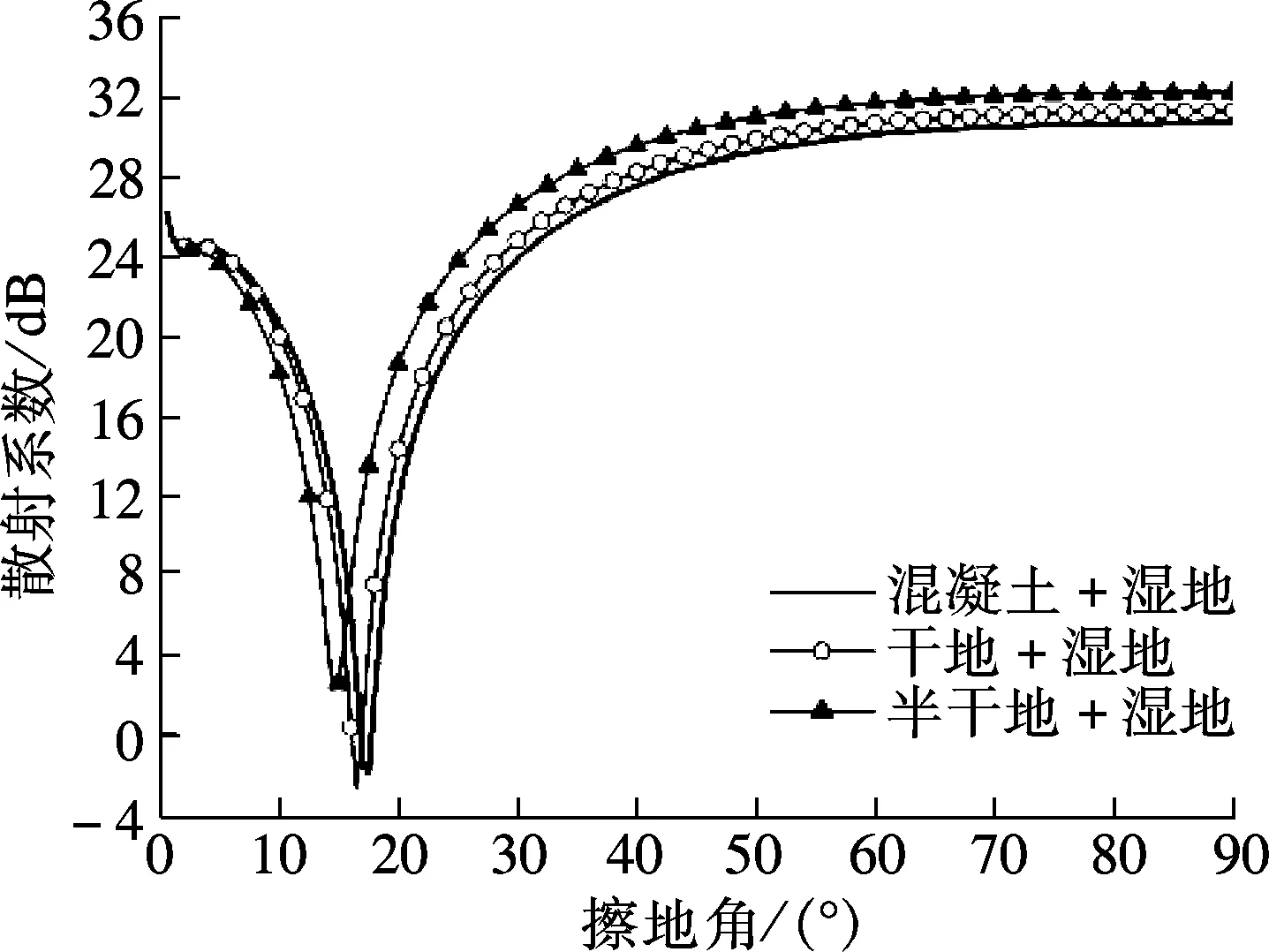
(c) hrms=0.1λ, lx=ly=3.0λ

由图5(a)可知,对于混凝土+湿地、干地+湿地、半干地+湿地表面,φB=19°,φB=18.5°,φB=16.5°．以混凝土+湿地表面为例,当统计参数hrms=0.1λ,lx=ly=1.0λ时,单一混凝土表面和单一湿地表面的φB分别为31.5°和13°,而混凝土+湿地双介质分区域复合粗糙面的φB为19°,该角度介于前两者之间,发生了布儒斯特角的融合现象,表明分区域复合粗糙面同时具备2种介质粗糙面的布儒斯特效应．观察半干地+湿地和半干地+湿地所对应的曲线,同样也发生了布儒斯特角的融合现象．

由图5(b)可知,对于混凝土+湿地、干地+湿地、半干地+湿地表面,其双介质分区域复合粗糙面的φB分别为27.5°，26.5°和25°．以混凝土+湿地表面为例,当统计参数hrms=0.3λ,lx=ly=1.0λ时,单一混凝土表面和单一湿地表面的φB分别为38°和21.5°,而混凝土+湿地双介质分区域复合粗糙面的φB为27.5°,该角度介于前两者之间,发生了布儒斯特角的融合现象,而在另外2组曲线中,也均发生了布儒斯特角的融合现象．比较图5(a)和(b)两组仿真结果发现,对于双介质分区域复合粗糙面,hrms的增加也会导致粗糙面布儒斯特角增大;且随着hrms的增加,其布儒斯特角逐渐展宽为布儒斯特角域,表明在双介质分区域复合粗糙面上也存在着布儒斯特展宽效应[11]．

由图5(b)可知,对于混凝土+湿地、干地+湿地、半干地+湿地表面,其双介质分区域复合粗糙面的φB分别为17.5°,16.5°和15°．以混凝土+湿地表面为例,当统计参数为hrms=0.1λ,lx=ly=3.0λ时,单一混凝土表面和单一湿地表面的φB分别为30°和10.5°,而混凝土+湿地双介质分区域复合粗糙面的φB为17.5°,该角度介于前两者之间,发生了布儒斯特角的融合现象,而在另2组曲线中,也均发生了布儒斯特角的融合现象．比较图5(a)和(c)两组仿真结果发现,对于双介质分区域复合粗糙面,l的增加也会导致粗糙面布儒斯特角的减小．

为考察表面sur1,sur2各自区域的hrms对整体分区域复合粗糙面布儒斯特效应的影响,令表面sur1,sur2分别为干地、湿地表面,用hsur1和hsur2分别表示其均方根高度,lsur1和lsur2分别表示其相关长度,且lsur1=l．仿真结果如图6(a)所示．

由图6(a)可知,对于干地+湿地双介质分区域复合粗糙面,当hsur1=hsur2=0.1λ时,φB=18.5°;当hsur1=hsur2=0.3λ时,φB=26.5°;当hsur1=0.1λ,hsur2=0.3λ时,φB=23°,该角度介于前两者之间．仿真结果表明,在双介质双重粗糙度分区域复合粗糙面上,不同均方根高度所对应的布儒斯特角存在着布儒斯特角的融合现象．

考察区域的相关长度l对整体表面布儒斯特效应的影响,固定sur1与sur2介质表面分别为干地与湿地表面,设置均方根高度hsur1=hsur2=0.1λ,仿真结果如图6(b)所示．由图可知,对于干地+湿地双介质分区域复合粗糙面,当lsur1=lsur2=1.0λ时,φB=18.5°;当lsur1=lsur2=3.0λ时,φB=16.5°;当lsur1=1.0λ,lsur2=3.0λ时,φB=17°,该角度介于前两者之间．仿真结果表明,在双介质双重粗糙度分区域复合粗糙面上,不同相关长度所对应的布儒斯特角存在着布儒斯特角的融合现象．

(a) 区域均方根高度改变

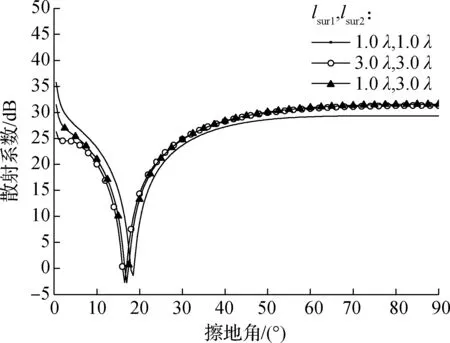
(b) 区域相关长度改变

综上可知,区域介电常数和区域粗糙度的改变均会引起布儒斯特角的融合现象,这是双介质双重粗糙度分区域复合粗糙面布儒斯特效应的新特性,即布儒斯特融合效应．这种融合效应是将各区域作为一个探测整体;若回归局部,各区域表面的布儒斯特角仍由各区域的粗糙程度、相对介电常数所确定．

2.3 三介质三重粗糙度分区域复合粗糙面

为考察各区域均方根高度hrms对三介质分区域复合粗糙面布儒斯特效应的影响,令表面sur1,sur2和sur3分别为干地表面、半干地面表面和湿地表面,用hsur3和lsur3分别表示表面sur3的均方根高度和相关长度,且lsur1=lsur2=lsur3=1.0λ,各粗糙面电尺寸相同．仿真结果如图7(a)所示．由图可知,对于干地+半干地+湿地三介质分区域复合粗糙面,当hsur1=hsur2=hsur3=0.1λ时,φB=19.5°;当hsur1=hsur2=hsur3=0.3λ时,φB=28°．由此表明,在三介质分区域复合粗糙面中,hrms的增加会导致粗糙面布儒斯特角增大．对于表面sur1,hsur1=0.3λ时,φB=20°;对于表面sur2,hsur2=0.3λ时,φB=20.5°;对于表面sur3,hsur3=0.3λ时,φB=23.5°．干地表面和半干地区域的hrms改变时,布儒斯特角的变化量分别为0.5°,1°;而湿地区域的hrms改变时,变化量为4°．导致变化量不相同的原因是各区域粗糙面的介质属性不同,湿地由于其复杂的介质构成和较高的含水量,相对介电常数和电导率均远大于干地和半干地,因此在各区域依次改变hrms时,布儒斯特角的变化在湿地区域最为明显．仿真结果表明,在三介质三重粗糙度分区域复合粗糙面中,介电常数占优的粗糙面区粗糙度改变所引起的布儒斯特融合效应最为显著．

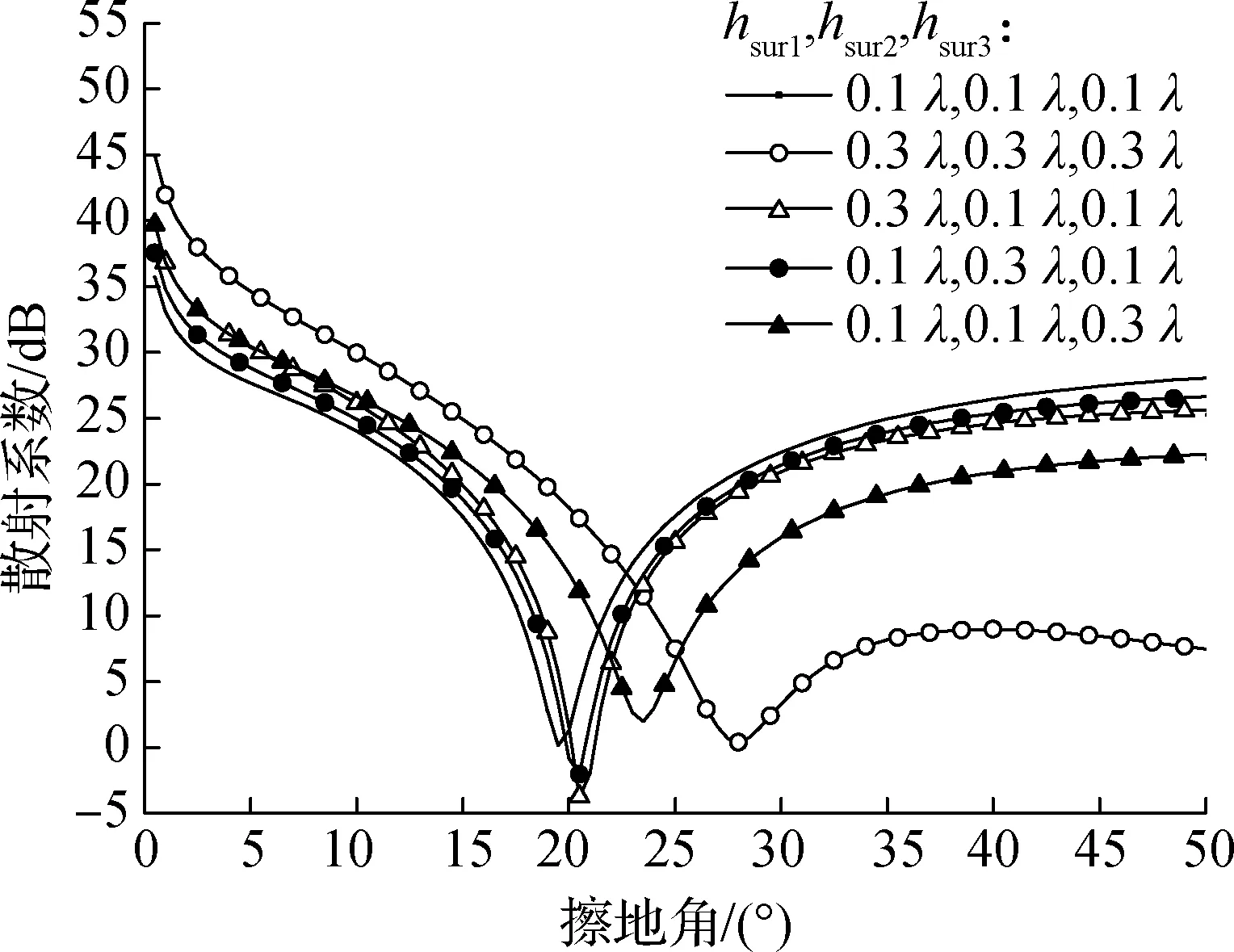
(a) 区域均方根高度改变

(b) 区域相关长度改变

考察各区域相关长度l对三介质分区域复合粗糙面布儒斯特效应的影响,固定表面sur1,sur2和sur3分别为干地表面、半干地面表面和湿地表面,设置粗糙面均方根高度hsur1=hsur2=hsur3=0.1λ,各粗糙面电尺寸相同．仿真结果如图7(b)所示．由图可知,对于干地+半干地+湿地三介质分区域复合粗糙面,当lsur1=lsur2=lsur3=1.0λ时,φB=19.5°;当lsur1=lsur2=lsur3=3.0λ时,φB=18°．由此表明,在三介质分区域复合粗糙面中,相关长度l的增加会导致粗糙面的布儒斯特角减小．对于表面sur1,lsur1=3.0λ时,φB=19.2°;对于表面sur2,lsur2=3.0λ时,φB=18.8°;对于表面sur3,lsur3=3.0λ时,φB=18.4°．干地表面和半干地区域相关长度改变时,布儒斯特角的变化量分别为0.3°,0.7°;湿地区域相关长度改变时,变化量为1.1°．受相对介电常数和电导率的影响,在各区域依次改变相关长度时,布儒斯特角的变化在湿地区域最为明显．仿真结果表明,在三介质三重粗糙度分区域复合粗糙面中,介电常数占优的粗糙面区域粗糙度改变所引起的布儒斯特融合效应最为显著．

综上可知,相关长度l变化所带来的布儒斯特角变化量小于均方根高度hrms所带来的变化量,并且随着分块区域数量的增加,相关长度l变化所引起的变化量越小．这是因为相关长度l描述的是粗糙面上相邻点的相关程度,而均方根高度hrms描述的是整个粗糙面的高低起伏．后文将着重讨论均方根高度hrms对多介质多重粗糙度分区域复合粗糙面布儒斯特效应的影响．

2.4 多介质多重粗糙度分区域复合粗糙面

为考察各区域均方根高度hrms对多介质分区域复合粗糙面布儒斯特效应的影响,令表面sur1,sur2,sur3和sur4分别为混凝土表面、干地表面、半干地面表面和湿地表面,用hsur4和lsur4分别表示表面sur4的均方根高度和相关长度,且lsur1=lsur2=lsur3=lsur4=1.0λ,各粗糙面电尺寸相同．仿真结果如图8所示．将图例中所示的6种表面结构编号为Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ．

由图8可知,当混凝土+干地+半干地+湿地多介质分区域复合粗糙面在表面结构分别为Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ时,布儒斯特角分别为21.5°,30°,22°,23.5°,24.5°,28°．比较结构Ⅰ和Ⅱ的布儒斯特角可知,在多介质分区域复合粗糙面中,均方根高度的增加会导致粗糙面布儒斯特角增大．比较结构Ⅰ和Ⅲ的布儒斯特角可知,即使某一介质区域所占比例较小,hrms的改变也会引起相应的布儒斯特融合效应．比较结构Ⅲ,Ⅳ,Ⅴ的布儒斯特角可知,随着均方根高度hrms=0.3λ的区域数量增加,所引起的布儒斯特融合效应更为显著．比较结构Ⅲ和Ⅳ可知,当表面sur3的hrms由0.1λ变为0.3λ,所引起的布儒斯特角变化量为1.5°;比较结构Ⅳ和Ⅴ可知,当表面sur2的hrms由0.1λ变为0.3λ,所引起的布儒斯特角变化量为1°,该变化量小于表面sur3中hrms改变所引起的变化量,这是由于表面sur3的含水量略高于表面sur2,导致相对介电常数和电导率大于表面sur2．由此可知,介电常数占优的粗糙面区域粗糙度改变所引起的布儒斯特融合效应更为显著．比较结构Ⅳ,Ⅴ和Ⅵ,以Ⅳ为参照,表面sur2和sur4的粗糙度改变所引起的布儒斯特角变化量分别为1°和4.5°,这是由湿地区域的相对介电常数和电导率均远大于干地所引起的,再次验证了2.3节中的结论,即在多介质多重粗糙度分区域复合粗糙面中,介电常数占优的粗糙面区域粗糙度改变所引起的布儒斯特融合效应更为显著．

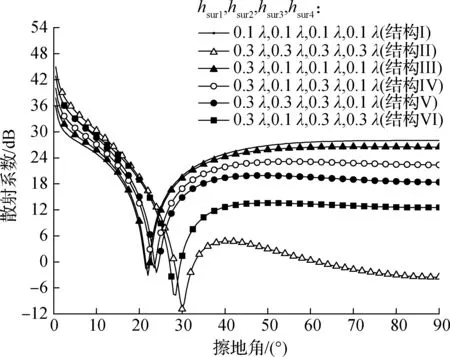
图8 多介质多重粗糙度分区域复合粗糙面布儒斯特效应

针对多介质、多粗糙度分区域复合粗糙面这一特殊表面结构,本文考察了入射方位角φin=45°,135°,225°,315°时表面结构Ⅲ的布儒斯特效应,发现所得的仿真曲线基本一致,布儒斯特角度均在同一位置．究其原因在于,布儒斯特效应是随机表面一种整体的电磁散射特性,不随探测方位角变化而变化,这与文献[9]中的散射系数定义相符．因此,在多介质、多粗糙度的真实环境下,在防空武器及预警机雷达探测超低空目标时,不论其所处方位如何,均能够通过布儒斯特角以垂直极化波下视探测,从而在最大程度上减少由于环境作用所引起的多径干扰,以增强雷达在复杂环境下的超低空目标探测能力．

3 结论

1) 针对真实自然环境的复合性、复杂性和分区域性,基于分区域复合粗糙面建模理论,实现了多介质、多粗糙度环境的模拟．

2) 在计算方法方面,考虑到面元间的相互耦合以及表面介质不一定满足阻抗边界条件,提出了一种适用于该类复杂分区域复合粗糙面的自适应迭代物理光学法．

3) 分别对双介质双重粗糙度、三介质三重粗糙度以及多介质多重粗糙度分区域复合粗糙面的布儒斯特效应进行了分析．仿真结果表明,区域介电常数和区域粗糙度的改变会引起布儒斯特融合效应,介电常数占优的区域粗糙度改变所引起的布儒斯特融合效应更为显著．

参考文献(References)

[1] Zilman G, Zapolski A, Marom M. On detectability of a ship’s kelvin wake in simulated SAR images of rough sea surface[J].IEEETransactionsonGeoscienceandRemoteSensing, 2015,53(2):609-619. DOI:10.1109/tgrs.2014.2326519.

[2] Voronovich A G, Zavorotny V U. Full-polarization modeling of monostatic and bistatic radar scattering from a rough sea surface[J].IEEETransactionsonAntennasandPropagation, 2014,62(3):1362-1371. DOI:10.1109/tap.2013.2295235.

[3] El-Bah S, Dusseaux R, Afifi S. Some statistical and spatial properties of signal scattering by 2-D slightly rough random surfaces[J].IEEETransactionsonAntennasandPropagation, 2016,64(2):721-729. DOI:10.1109/tap.2015.2511803.

[4] Wei P B, Zhang M, Sun R Q, et al. Scattering studies for two-dimensional exponential correlation textured rough surfaces using small-slope approximation method[J].IEEETransactionsonGeoscienceandRemoteSensing, 2014,52(9):5364-5373. DOI:10.1109/TGRS.2013.2288278.

[5] Johnson J T, Burkholder R J, Toporkov J V, et al. A numerical study of the retrieval of sea surface height profiles from low grazing angle radar data[J].IEEETransactionsonGeoscienceandRemoteSensing, 2009,47(6): 1641-1650. DOI:10.1109/tgrs.2008.2006833.

[6] 李昌泽, 童创明, 齐立辉, 等. 三类新型随机粗糙面模型的快速散射特性分析[J]. 电波科学学报, 2015, 30(6): 1093-1101. DOI:10.13443/j.cjors.2015012901. Li Changze, Tong Chuangming, Qi Lihui, et al. Analysis on fast electromagnetic scattering characteristics for three novel randomly rough surface models[J].ChineseJournalofRadioScience, 2015,30(6): 1093-1101. DOI:10.13443/j.cjors.2015012901.(in Chinese)

[7] Sun H L, Tong C M, Zou G X. High efficiency iterative solver for modeling composite rough surface electromagnetic scattering[J].Electromagnetics, 2017,37(2):113-126. DOI:10.1080/02726343.2017.1279113.

[8] 邹高翔, 童创明, 王童, 等. 地海交界分区域复合粗糙面建模及电磁散射特性研究[J]. 系统工程与电子技术, 2017, 39(7):43-56.

Zou Gaoxiang, Tong Chuangming, Wang Tong, et al. Study on modeling and electromagnetic scattering characteristics of composite rough surface of ground and ocean in adjacent region[J].SystemsEngineeringandElectronics, 2017,39(7):43-56. (in Chinese)

[9] 邹高翔, 童创明, 孙华龙,等. 地海交界分区域复合粗糙面的布儒斯特效应研究[J]. 电波科学学报, 2016, 31(6):1036-1045. Zou Gaoxiang, Tong Chuangming, Sun Hualong, et al. Brewster effect from composite rough surface of ground and sea in adjacent region[J].ChineseJournalofRadioScience, 2016,31(6):1036-1045. (in Chinese)

[10] Saillard M, Maystre D. Scattering from metallic and dielectric rough surfaces[J].JournaloftheOpticalSocietyofAmericaA, 1990,7(6):982-990. DOI:10.1364/josaa.7.000982.

[11] Baylard C, Maradudin A A, Greffet J J. Coherent reflection factor of a random rough surface: applications[J].JournaloftheOpticalSocietyofAmericaA, 1993,10(12):2637-2647. DOI:10.1364/josaa.10.002637.

[12] Trizna D B. A model for Brewster angle damping and multipath effects on the microwave radar sea echo at low grazing angles[J].IEEETransactionsonGeoscienceandRemoteSensing, 1997,35(5): 1232-1244. DOI:10.1109/36.628790.

[13] Thomson L I, Osinski G R, Pollard W H. Application of the Brewster angle to quantify the dielectric properties of ground ice formations[J].JournalofAppliedGeophysics, 2013,99: 12-17. DOI:10.1016/j.jappgeo.2013.08.015.

[14] 隋栋训, 童创明, 彭鹏, 等. 超低空目标的广义布儒斯特效应[J]. 空军工程大学学报(自然科学版), 2015, 16(4): 29-32. DOI:10.3969/j.issn.1009-3516.2015.04.007. Sui Dongxun, Tong Chuangming, Peng Peng, et al. A study of g brewster of super low altitude target[J].JournalofAirForceEngineeringUniversity(NaturalScienceEdition), 2015,16(4): 29-32. DOI:10.3969/j.issn.1009-3516.2015.04.007.(in Chinese)

[15] Ye H, Jin Y Q. Parameterization of the tapered incident wave for numerical simulation of electromagnetic scattering from rough surface[J].IEEETransactionsonAntennasandPropagation, 2005,53(3):1234-1237. DOI: 10.1109/TAP.2004.842586

[16] Chin H, Yeom J H, Kim H T, et al. Improvement of iterative physical optics using previous information to guide initial guess[J].ProgressinElectromagneticsResearch, 2012,124: 473-486. DOI:10.2528/pier12011103.

Brewstereffectofcomplicatedcompositeroughsurface

Zou Gaoxiang1Tong Chuangming1,2Sun Hualong1Peng Peng1,3Wang Tong1

(1Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China) (2State Key Laboratory of Millimeter Waves, Southeast University, Nanjing 210096, China) (3School of Physics and Optoelectronic Engineering, Xidian University, Xi’an 710071, China)

TN011

A

1001-0505(2017)05-0897-09

2016-12-28.

邹高翔(1993—)，男，博士生；童创明(联系人)，男，博士，教授，博士生导师，cmtong156@126.com.

国家自然科学基金资助项目(61372033).

邹高翔,童创明,孙华龙,等.复杂分区域复合粗糙面的布儒斯特效应[J].东南大学学报(自然科学版),2017,47(5):897-905.

10.3969/j.issn.1001-0505.2017.05.010.

10.3969/j.issn.1001-0505.2017.05.010