W波段低旁瓣波导缝隙行波阵天线

檀 雷 张 剑 王文博 徐金平

(东南大学毫米波国家重点实验室, 南京 210096)

W波段低旁瓣波导缝隙行波阵天线

檀 雷 张 剑 王文博 徐金平

(东南大学毫米波国家重点实验室, 南京 210096)

针对W波段波导缝隙天线加工难度高、加工后缝隙尺寸不易修改的问题,提出了一种改进型缝隙电导函数提取方法．首先,根据工艺可实现性,设定合理的波导辐射面壁厚和缝隙宽度;然后,应用HFSS软件计算出不同缝隙切入深度和缝隙倾斜角度的缝隙电导值;最后,利用Matlab软件拟合出电导函数曲线,并进行阶梯状的分段近似,以简化加工工艺复杂度．基于优化设计结果,加工出4套天线样品,采用紧缩场测试方法对天线进行辐射方向图测量．结果表明,在75～79 GHz的频带内,天线增益均大于23.5 dBi,E面3 dB波束宽度为1.2°,旁瓣电平低于-20 dB．当频率从75 GHz扫描至79 GHz时,E面3 dB波束覆盖范围为5.5°．4套天线的性能测试结果展现出较好的一致性,从而验证了设计方法的正确性和有效性．

波导缝隙天线;行波阵;低旁瓣;波束扫描;紧缩场

Abstract: To solve the problem of the high processing difficulty of W-band slotted-waveguide antennas and the difficulty of modifying the gap size after processing, an improved method for extracting the conductance function of the slot is proposed.First,according to the process feasibility, the wall thickness of the waveguide and the width of the slot are reasonably pre-determined. Then,the HFSS software is employed to calculate the conductances of the slots with different cutting depths and inclination angles.Finally,the conductance function curve is drawn by the Matlab soft, and the piecewise approximation is performed to simplify machining complexity. Based on the optimized design results, four sets of antennas are fabricated and tested by the compact range measurement method in an anechoic chamber.The results show that in the frequency coverage from 75 to 79 GHz, the gain of the slotted waveguide antenna is higher than 23.5 dBi, and in E-plane the 3 dB beam width and the side lobe level are 1.2° and -20 dB, respectively. The 3 dB beam scanning range in E-plane is 5.5° when the frequency sweeps from 75 to 79 GHz. The measured performances of the four sets of antennas agree well with each other, which verifies the correctness and the effectiveness of the proposed method.

Keywords: slotted-waveguide antenna; traveling-wave array;low side lobe; beam scanning; compact range

波导缝隙天线因其馈电简单、损耗小、效率高、易实现低旁瓣等特点,广泛应用于雷达和通信系统中[1-4]．该类天线可分为谐振式(驻波阵)和非谐振式(行波阵)2种形式．在非谐振式波导缝隙阵列中,电磁波近似行波传播,天线能在较宽的频带上保持良好的匹配,并且波束指向随频率变化．因此,带宽较宽且具有波束扫描功能的波导缝隙行波阵天线特别适合于FMCW雷达的相关应用．

毫米波波长短,在相同的物理口径下,毫米波天线具有比微波天线窄得多的波束,从而为毫米波目标探测和成像系统提供更高的精度和分辨力．然而,毫米波波导缝隙天线存在加工难度高、加工成形后缝隙尺寸不易修改的固有缺点,限制了其在实际工程中的推广应用．若要成功设计出毫米波波导缝隙天线,必须综合考虑各种影响因素,正确选择设计方法,以国内现有精密加工水平为前提,精确计算各缝隙参数．

本文针对毫米波FMCW雷达目标探测系统,研制了一款W波段76个缝隙单元的波导缝隙行波阵馈源天线．考虑到毫米波波导缝隙天线加工精度要求高,且加工完成后各缝隙尺寸不易修改的特点,本文改进了缝隙电导函数的提取过程,在使用计算机辅助提取电导函数之前,先根据工艺可实现性确定合适的波导辐射面壁厚和缝隙宽度．此外,对最终获得的电导函数曲线进行阶梯状的分段近似,以便于实际加工．所设计的天线在E面具有窄波束和低旁瓣,使得探测系统具有较高的角分辨率,而该类天线固有的波束扫描功能,又能增加系统扫描方式的灵活性．

1 分析与设计

本文设计的W波段波导缝隙行波阵天线采用窄边开缝的形式,其结构示意图及关键尺寸如图1所示．图中,a和b分别为矩形波导宽边和窄边尺寸;φ为缝隙倾斜角度;w为缝隙宽度;d为缝隙间距;h为缝隙切入深度;t为辐射面波导壁厚．

天线工作时,电磁波由馈电端口输入,大部分能量经缝隙辐射出去,剩余小部分能量被匹配负载吸收．电磁波在整个波导内近似行波传播,使得天线能在较宽的频带范围内保持良好的匹配．由于各缝隙均处于行波激励状态,缝隙间具有线性相差,使得最大波束指向偏离阵列法线方向,且随频率变化,从而实现波束扫描的功能．

设计时,首先根据扫描角度与频率的对应关系,计算出缝隙间距;其次根据副瓣电平的要求,选取合适的分布函数对天线阵元进行综合,并计算出各个缝隙的激励电流幅度分布;然后根据功率传输法,确定每个缝隙的理论电导值;最后借助仿真软件,建立参数提取模型,确定缝隙电导值与缝隙尺寸的关系,即确定缝隙电导函数,并由此计算出每个缝隙的具体尺寸．

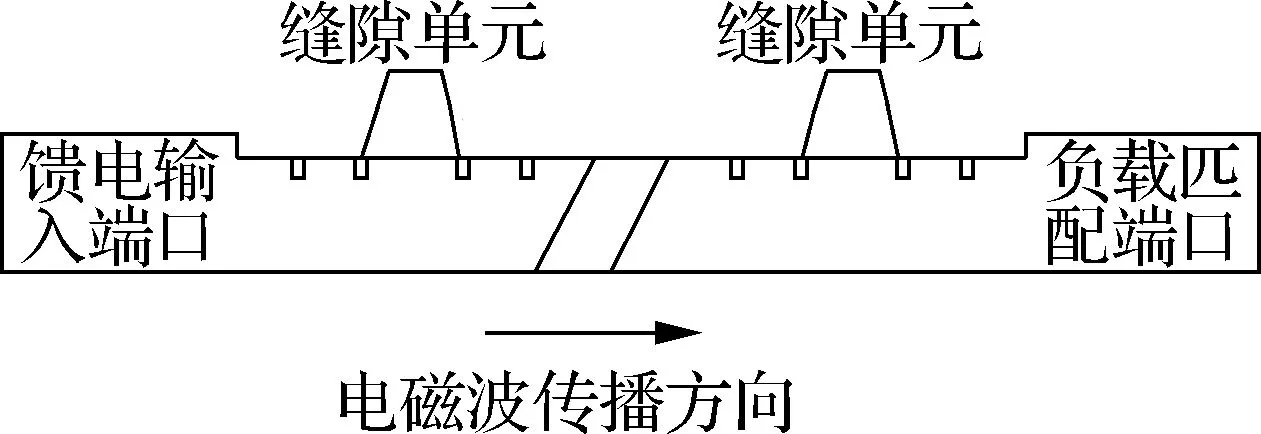
(a) 侧视图

(b) 俯视图

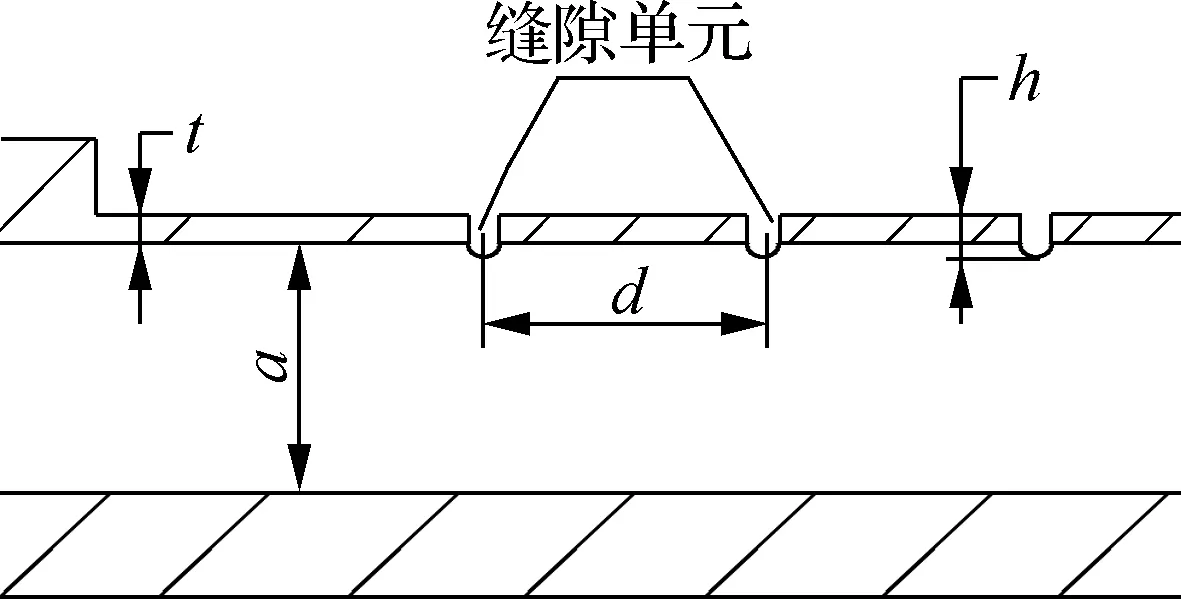
(c) 剖视图

1.1 缝隙间距的确定

设θ为波束指向角,其定义为天线最大辐射方向与天线法向的夹角．则缝隙间距与波束指向角的关系为

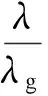
(1)

式中,λ和λg分别为对应于中心频率77 GHz处的工作波长和波导波长．根据式(1)以及所要求的波束指向与频率的对应关系,可以计算出缝隙间距．

1.2 旁瓣电平的优化

为了降低旁瓣电平,本文采用泰勒综合法对天线方向图进行综合．根据阵列天线相关理论,泰勒线阵各单元的激励电流幅度可表示为[5]

(2)

式中,L为线阵长度;n表示缝隙单元序号;Sn(m)为泰勒分布的方向图函数,且

(3)

(4)

参数σ为波瓣展宽因子,且

(5)

式中,R0为主副瓣电平比．考虑到旁瓣电平的最终设计要求为小于-20 dB,此处将理想的泰勒分布旁瓣电平按小于-30 dB进行设计．由此便可计算得到,主副瓣电平之比为31.62,等副瓣个数为5,波瓣展宽因子等于1.07．

当线阵长度L远大于工作波长λ时,泰勒分布方向图的半功率波束宽度可表示为[5]

(6)

式中,N为缝隙总数.

根据半功率波束宽度设计要求,并考虑到终端负载、馈电端波导法兰、天线长度等尺寸的影响,最终确定缝隙总数N=76．应用数学软件Matlab对泰勒综合法中的理论公式进行编程,便可计算得到各缝隙单元的归一化激励电流幅度(见图2)．

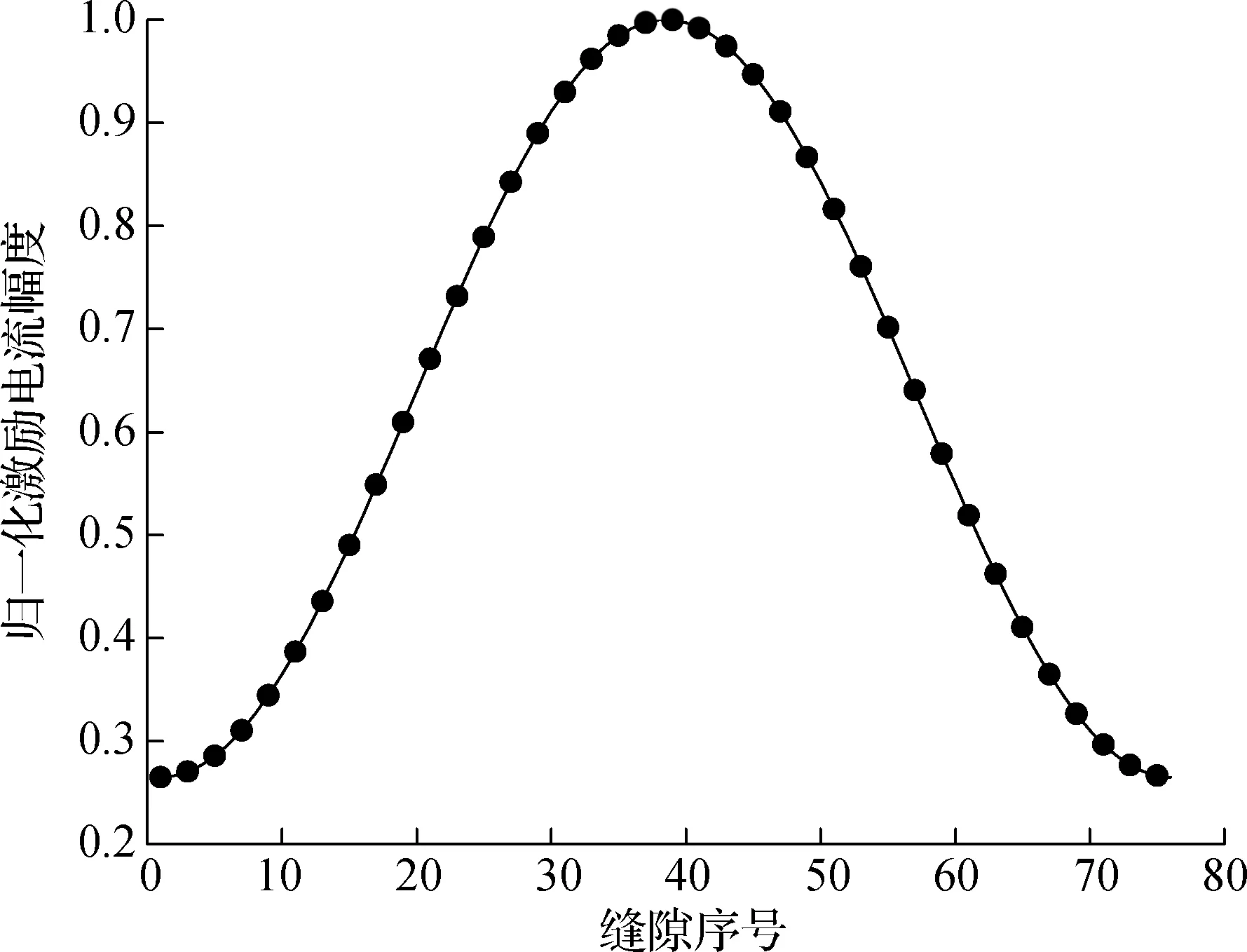
图2 归一化激励电流幅度分布

1.3 各缝隙电导值的确定

设波导衰减常数为α,则波导内传输的行波功率经过一段距离z后,功率能量减小为原来的q倍,即

q=e-2αz

(7)

根据功率传输法[6],以及图2中每个缝隙的激励电流幅度,可计算出每个缝隙的归一化电导值为

(8)

式中,gn为第n个缝隙单元的缝隙电导值;η为天线效率．

需要注意的是,计算得到的gn有一上限值gmax,其主要原因在于:① 较小的gn才能保证缝隙对波导为弱耦合,从而使得波导内近似行波传输;② 对于窄边开缝的波导缝隙天线,其缝隙的倾斜角度直接关系到谐振电导值．在W波段,窄边波导缝隙天线的最大缝隙倾角不宜超过17°,即过大的gn在工程上难以实现．当计算出的gn最大值超过gmax时,应适当降低天线效率,重新进行计算．根据1.2节中计算出的归一化激励电流幅度分布,并考虑最大缝隙倾角的工艺限制,根据式(8)可计算出76个缝隙的归一化电导值(见图3)．此时天线辐射效率为91%,对应的gmax为0.082．

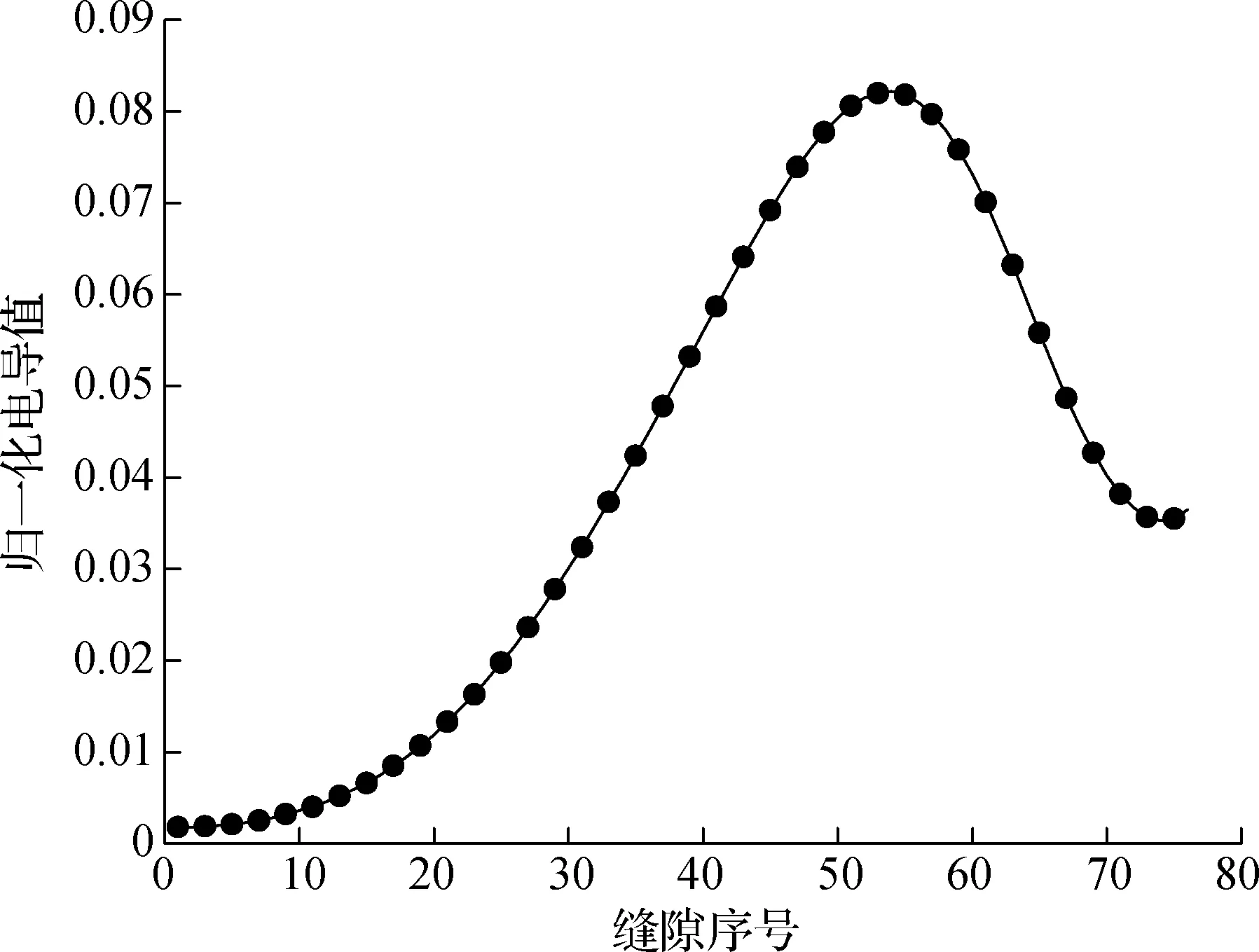
图3 归一化电导值分布

1.4 缝隙电导函数的确定

缝隙电导函数计算精确与否是设计这类天线的主要难点．获取缝隙电导函数的传统方法主要分为数值计算法和实验测量法．数值计算法对缝隙之间的互耦考虑不充分[7-8],而实验方法的设计工作量和误差又太大．随着电磁仿真软件的不断发展,利用计算机辅助设计来求取缝隙电导函数的方法,不仅减少了实验法所需的工作量,而且还充分考虑了缝隙间的互耦．

在低频段,利用电磁仿真软件进行电导函数辅助提取时,诸如缝隙宽度和辐射面波导壁厚这类参数通常不需要单独考虑,只要在后续软件优化计算电导函数时综合考虑即可．但随着频率提升至W波段,设计中必须考虑到加工工艺的影响,因此在提取电导函数之前,需要确定合理的、工艺上可实现的缝隙宽度和辐射面波导壁厚．

缝隙宽度的确定首先要满足功率容量的要求[9],一般在W波段,缝隙宽度大于工作波长的1/20即可．其次,缝隙宽度的大小还会影响给定缝隙倾斜角度下谐振电导值．图4给出了缝隙宽度w对归一化缝隙电导值的影响．

图4 缝隙宽度对归一化缝隙电导值影响

由4可以看出,对于相同的缝隙倾斜角度,缝隙宽度越小,对应的谐振电导值越大．能加工的缝隙倾斜角度最大值是有限的,故而窄的缝隙宽度能获得更大的谐振电导值,相应的辐射效率也更高．同时还必须考虑到工艺水平的限制,在W波段,综合考虑加工难度与成本,设计过程中选定缝隙宽度的初始尺寸为0.3 mm．

对于辐射面波导壁厚的选取,在低频段(如C波段、X波段),通常取为1 mm;而在W波段,1 mm 的波导壁厚已经和波导波长处于同一量级,必须考虑其影响．图5给出了辐射面波导壁厚t对归一化缝隙电导值的影响．从图中可以看出,随着壁厚的增加,缝隙处于谐振状态下的最大电导值逐渐变小．由于加工工艺限制了缝隙的最大倾斜角度,若要保证天线效率,则辐射面壁厚不能太厚．此外,从图中还可以看出,随着壁厚的增加,缝隙处于谐振状态时的切入深度逐渐减小,这意味着当壁厚增加至一定值后,该缝隙倾斜角度下的谐振电导值将不易提取．

图5 辐射面壁厚对归一化缝隙电导值影响

随着辐射面壁厚的增加,天线效率逐渐降低,且还会对电导函数的提取带来困难．对辐射面壁厚的选择既要考虑到其对电性能的影响和电导函数提取的难度,又要考虑到结构强度和加工难度．设计中选定辐射面壁厚的初始尺寸为0.3 mm．

在确定了缝隙数目、缝隙间距、缝隙宽度和辐射面波导壁厚这些参数之后,可以进行缝隙电导函数的提取工作．利用行波近似法和微波网络相关理论,得到缝隙电导值和S参数之间的关系为

(9)

式中,r为匹配负载相对吸收功率,可由参数S表示为

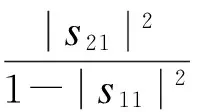
(10)

式中,s11和s21分别为该天线的输入端反射系数和正向传输系数．

使用HFSS提取电导函数,先在波导窄边上开76个切入深度相同、倾斜角度相同且交替反向排列的缝隙;其次,固定缝隙倾角,对切入深度进行参数扫描,根据式(9)得到不同切入深度所对应的电导值,其中最大电导值对应的切入深度即为缝隙处于谐振状态下的最优值;然后,改变倾斜角度并重复以上步骤,得到不同倾斜角度所对应的最优切入深度和最大电导值;最后,应用Matlab软件对曲线进行拟合,即可得到需要的缝隙电导函数曲线．

1.5 优化设计

通过前面的分析,已经获得了所要设计的波导缝隙天线的缝隙间距、开缝数目、缝隙宽度、辐射面波导壁厚以及缝隙电导函数．在图6和图7中,离散点是通过电磁仿真软件提取出来的,而连续线则是后期通过Matlab软件拟合出来的．在拟合曲线时,对于图6,选取缝隙倾斜角度的精度为0.1°,即可较好地匹配拟合曲线．而在图7中,若要较好匹配拟合曲线,切入深度至少要精确到小数点后3位甚至4位,这样高的加工精度在W波段很难实现．因此,考虑到切入深度的加工精度最高为0.01 mm量级,本文将切入深度与倾斜角度的对应关系按照阶梯分布的形式进行处理,并且通过HFSS软件仿真验证了2种取值形式在最终的仿真结果上的差别.阶梯分布形式的具体取值见表1．

此外,在机械加工过程中,鉴于热变形、受力变形、刀具磨损、装夹误差等一系列原因,使得加工的天线尺寸与设计值不能完全吻合,总会出现一定的误差[10]．这种加工误差会导致天线的增益、旁瓣电平等电性能的变化,尤其是在W波段．因此,还需要在仿真优化中对缝隙间距、缝隙倾角和切入深度等关键参数进行容差分析,最终优化后的W波段波导缝隙行波阵天线E面方向图仿真结果如图8所示．

图6 不同缝隙倾角对应的归一化谐振电导值

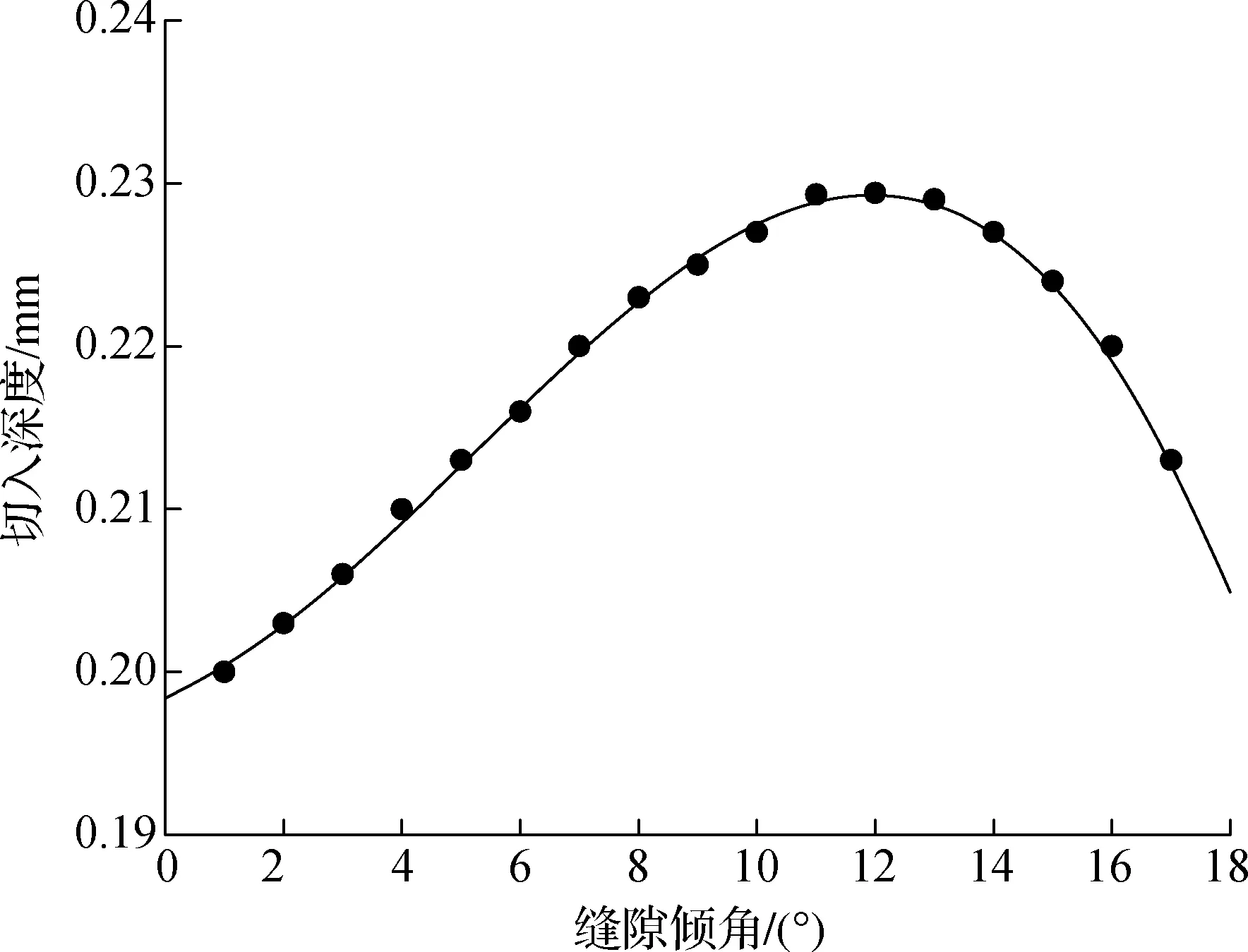
图7 不同缝隙倾角对应的最佳切入深度

缝隙倾角/(°)切入深度/mm0～2.80.202.8～5.80.215.8～9.00.229.0～14.60.2314.6～16.00.22

从仿真结果中可以看出,该波导缝隙行波阵天线在工作频率75～79 GHz的范围内,增益大于25 dBi,E面3 dB波束宽度为1.2°,副瓣电平低于-23 dB,半功率波束扫描覆盖范围约为5.5°．

值得注意的是,上述仿真结果中75 GHz时的副瓣电平在-23 dB以下,77和79 GHz的副瓣电平小于-25 dB．这与-30 dB的理想泰勒分布副瓣电平值存在一定差距,究其原因在于:① 1.2节中理想的泰勒分布是针对中心频率77 GHz进行设计的,这会导致高频和低频处的副瓣电平发生恶化,因此在仿真优化时调整了天线的口径分布,使得整个工作频段内的副瓣电平都能达到一个较为合理的值;② 天线两端的缝隙和中间缝隙的耦合环境不同,需要在仿真优化时,对天线口径分布进行局部调整,以便同时兼顾辐射效率和副瓣电平,即最终的天线口径分布并非完全按照之前理论计算的结果来设计,从而产生了副瓣电平的仿真结果与理论计算值之间的偏差．

图8 天线E面方向图仿真结果

2 天线测试与结果分析

基于第1节中的设计优化工作,本文加工了4套W波段波导缝隙行波阵天线样品,实物图见图9．

图9 W波段波导缝隙行波阵天线实物照片

根据天线辐射远场条件可知

(11)

式中,R为实际远场测试时接收天线距待测天线的距离;D为天线物理口径的最大尺寸．

由式(11)可计算出该天线的远场测试条件为R≥46 m,故普通的微波暗室无法完成远场测量．然而,室外远场测试受到周围环境电磁干扰、地面反射、气候条件等因素的影响,难以保证较高的测量精度．因此,采用W波段紧缩场对天线进行远场辐射方向图测量．

实测得到的天线E面方向图见图10,驻波比及增益测试结果见图11．从测试结果可以看出,在75～79 GHz的工作频率范围内,天线增益大于23.5 dBi,驻波比小于1.2∶1,E面的3 dB波束宽度为1.2°,旁瓣电平低于-20 dB,3 dB波束扫描覆盖范围约为5.5°．

图10 天线E面方向图测试结果

图11 天线增益及输入驻波比测试结果

通过比较图8和图10可见,天线的E面3 dB波束宽度及波束扫描覆盖范围的仿真结果和实测结果基本一致．从图11中可以看出,实测的增益比仿真值低1.5 dB左右,驻波比典型值为1.1∶1．考虑到加工、装配、波导损耗及测试的误差,实测结果和仿真结果一致性良好,且4套天线的性能差异较小．

3 结论

1) 提出了一种改进型缝隙电导函数提取方法．

2) 基于该方法设计加工了4套W波段波导缝隙行波阵天线，实测结果和仿真结果具有很好的一致性,从而验证了整个波导缝隙天线设计与仿真过程的可靠性和准确性．

3) 所研制的W波段波导缝隙行波阵天线具有窄波束、低副瓣、波束指向随频率变化的特点,适于毫米波FMCW雷达的相关应用．

References)

[1] Kumar P, Kedar A, Singh A K. Design and development of low-cost low sidelobe level slotted waveguide antenna array in X-Band[J].IEEETransactionsonAntennasandPropagation, 2015,63(11): 4723-4731. DOI:10.1109/tap.2015.2475632.

[2] Park S, Tsunemitsu Y, Hirokawa J, et al. Center feed single layer slotted waveguide array[J].IEEETransactionsonAntennasandPropagation, 2006,54(5): 1474-1480. DOI:10.1109/tap.2006.874310.

[3] Coetzee J C, Joubert J, McNamara D A. Off-center-frequency analysis of a complete planar slotted-waveguide array consisting of subarrays[J].IEEETransactionsonAntennasandPropagation, 2000,48(11): 1746-1755. DOI:10.1109/8.900233.

[4] 任宇辉, 高宝建, 伍捍东, 等. 基于CST的波导窄边缝隙天线的分析与设计[J]. 西北大学学报(自然科学版), 2010, 40(5): 798-801. Ren Yuhui, Gao Baojian, Wu Handong, et al. Analysis and design of the slotted antenna in the narrow wall of a rectangular waveguide based cst[J].JournalofNorthwestUniversity(NaturalScienceEdition), 2010,40(5): 798-801.(in Chinese)

[5] 汪茂光,吕善伟,刘瑞祥.阵列天线分析与综合[M].成都:西安电子科技大学出版社,1989:87-89.

[6] 林昌禄.天线工程手册[M]. 北京:电子工业出版社，2002:295-296.

[7] Elliott R, Kurtz L. The design of small slot arrays[J].IEEETransactionsonAntennasandPropagation, 1978,26(2): 214-219. DOI:10.1109/tap.1978.1141814.

[8] Stevenson A F. Theory of slots in rectangular wave-guides[J].JournalofAppliedPhysics, 1948,19(1): 24-38. DOI:10.1063/1.1697868.

[9] 沈铁汉.天线雷达设备[M].西安:通信兵雷达工程学院，1963:105-109.

[10] 周琴. 加工误差产生的原因及分析[J]. 现代机械, 2011(2): 8-10,13. DOI:10.3969/j.issn.1002-6886.2011.02.003. Zhou Qin. Reasons and analysis of machining deviation[J].ModernMachinery, 2011(2): 8-10,13. DOI:10.3969/j.issn.1002-6886.2011.02.003.(in Chinese)

W-bandslotted-waveguidetravellingarrayantennawithlowsidelobe

Tan Lei Zhang Jian Wang Wenbo Xu Jinping

(State Key Laboratory of Millimeter Waves, Southeast University, Nanjing210096, China)

TN823.24

A

1001-0505(2017)05-0850-06

2017-04-01.

檀雷(1986—),男,博士生;徐金平(联系人),男,博士，教授,博士生导师,jpxu@seu.edu.cn.

檀雷,张剑,王文博,等.W波段低旁瓣波导缝隙行波阵天线[J].东南大学学报(自然科学版),2017,47(5):850-855.

10.3969/j.issn.1001-0505.2017.05.002.

10.3969/j.issn.1001-0505.2017.05.002