广义可能性计算树逻辑和计算树逻辑的关系*
李 丹,李永明
陕西师范大学 计算机科学学院,西安 710119
广义可能性计算树逻辑和计算树逻辑的关系*
李 丹,李永明+
陕西师范大学 计算机科学学院,西安 710119
Abstract:Generalized possibilistic computation tree logic(GPoCTL)plays an important role in model checking with uncertainty,there is still further research in its expressiveness.In order to study the expressiveness of GPoCTL,this paper discusses the relationship between GPoCTL and computation tree logic(CTL)with respect to their expressiveness.Firstly,this paper defines interval generalized possibilistic computation tree logic(IGPoCTL),and gives the definition of the equivalence between IGPoCTL formulae and CTL formulae,and proves that CTL is a proper subclass of IGPoCTL.Because IGPoCTL is obviously a simple crispness of GPoCTL,CTL can be regarded as a proper subclass of GPoCTL.Besides,this paper gives the definition ofα-equivalence between IGPoCTL formulae and CTL formulae and gets some more general results.
Key words:computation tree logic;generalized possibilistic computation tree logic;interval generalized possibilistic computation tree logic;expressiveness
广义可能性计算树逻辑(generalized possibilistic computation tree logic,GPoCTL)在不确定性模型检测中扮演着非常重要的角色,但其表达能力还尚未研究全面。为此,讨论了GPoCTL与计算树逻辑(computation tree logic,CTL)表达能力之间的关系。首先定义了区间广义可能性计算树逻辑(interval generalized pos-sibilistic computation tree logic,IGPoCTL),并给出了IGPoCTL公式和CTL公式等价的定义。然后证明了CTL是IGPoCTL的一个真子类,因为IGPoCTL是GPoCTL的一种简单分明化形式,则CTL可看作GPoCTL的一个真子类。此外,还给出了IGPoCTL公式和CTL公式α-等价的定义,并得出了一些更一般的结果。
计算树逻辑;广义可能性计算树逻辑;区间广义可能性计算树逻辑;表达能力
1 引言
模型检测[1-4]是一种形式化的自动验证技术,它主要由以下3步组成:(1)抽象出系统的数学模型;(2)对需要验证的属性进行形式化描述;(3)通过模型检测算法来验证系统是否满足该属性,若满足,则返回“是”;若不满足,将会给出一个反例。模型检测现已被广泛地应用于计算机系统的设计和分析中[5-6]。
1986年Hart和Sharir[7]提出了将概率理论应用到系统的模型检测中;Baier和Katoen[2]在此基础上,介绍了以马尔科夫链为模型的基于概率测度的模型检测。随后,一些学者提出在状态模型中引入更多的量化信息,如在模型中引入统计信息[8]或者多值信息[9-10],以及在状态中引入时间信息[2]。1965年Zadeh提出了模糊集理论[11-13],并引入可能性测度的概念。李永明等人率先将可能性测度与模型检测结合,提出了基于可能性测度的模型检测[14-17];但它具有极大的局限性,为了解决更一般的不确定性问题,又进一步提出了基于广义可能性测度的模型检测[18-19],目前该理论还在不断完善中。
模型检测需要将系统属性形式化地描述为不同的逻辑公式。对于这些逻辑公式,它们的表达能力不同,采用表达能力强的逻辑公式能够拓广模型检测的适用范围。然而,对于广义可能性计算树逻辑(generalized possibilistic computation tree logic,GPoCTL)的表达能力的研究尚不全面,文献[19]比较了GPoCTL和可能性计算树逻辑(possibilistic computation tree logic,PoCTL)的表达能力,并得出GPoCTL的表达能力强于PoCTL。本文定义了IGPoCTL,并比较了IGPoCTL和CTL的表达能力。
本文组织结构如下:第2章介绍了一些基本概念;第3章比较了IGPoCTL和CTL的表达能力;第4章总结全文。
2 预备知识
本章给出经典计算树逻辑和基于广义可能性测度下计算树逻辑的概念,包括Kripke结构、CTL的语构和语义、广义可能性Kripke结构和GPoCTL的语构和语义等。
定义1[2]一个Kripke结构(Kripke structure,KS)M=(S,→,I,AP,L)是一个五元组,其中:
(1)S是一个可数非空的状态集合;
(2)→⊆S×S是状态转移关系,并且要求→是全关系,即对任意s∈S,存在t∈S,使得(s,t)∈→;
(3)I⊆S是初始状态的集合;
(4)AP是原子命题的集合;
(5)L:S→2AP是状态的标签函数,表明每个状态s所满足的原子命题的集合。
定义2[2](CTL的语构)CTL状态公式按照如下规则定义:
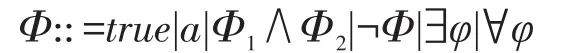
其中,φ是CTL路径公式,a∈AP。
CTL路径公式按照如下规则定义:

其中,Φ、Φ1和Φ2是CTL状态公式。
定义3[2](CTL的语义)设M=(S,→,I,AP,L)是一个KS,a∈AP,s∈S,Φ1和Φ2是CTL状态公式,φ是CTL路径公式,π=s0s1s2…是M中的任意一条路径,对任意的i≥0,记π[i]=si。则状态公式的满足关系定义为:

路径公式的满足关系定义为:
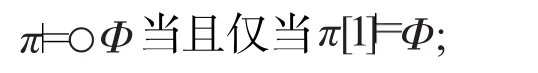

定义4[2]对于a∈AP,存在范式(existential normal form,ENF)的CTL状态公式定义如下:

定义5[19]一个广义可能性Kripke结构(generalized possibilistic Kripke structure,GPKS)M=(S,P,I,AP,L)是一个五元组,其中:
(1)S是一个可数非空的状态集合;
(2)P:S×S→[0,1]是可能性转移分布函数;
(3)I:S→[0,1]是可能性初始分布函数;
(4)AP是原子命题的集合;
(5)L:S×AP→[0,1]是可能性标签函数,若a∈AP,s∈S,则L(s,a)表示状态s满足原子命题a的可能程度。
若S和AP都是有限的,则M是有限的GPKS。
进一步,对任意的E⊆Paths(M),定义PoM(E)=∨{PoM(π)|π∈E},则可得扩张映射PoM:2Paths(M)→[0,1],并明的,即L:S×AP→{0,1},则M为GPKS[15-16],并称M是正规的。这里,∨和∧分别表示实数的上下确界。
(2)对于GPKSM,从状态s出发的一条路径可以用一组无限的状态序列来表示,即s0s1s2…,其中s0=s,以及∀i≥0,都有P(si,si+1)>0;从状态s出发的一条有限路径可以用一组有限的状态序列来表示,即s0s1s2…sn,其中s0=s,n≥0,以及对任意的0≤i≤n-1,有P(si,si+1)>0。Paths(s)是从状态s出发的所有路径所组成的集合;而Pathsfin(s)是从状态s出发的所有有限路径所组成的集合。Paths(M)是M中所有路径所组成的集合;而Pathsfin(M)是M中所有有限路径所组成的集合。
定义6[19]设M是一个GPKS,定义映射PoM:Paths(M)→[0,1],对任意的π=s0s1s2…∈Paths(M),有称PoM是Ω=2Paths(M)上的广义可能性测度。若M是明确的,则PoM可简记为Po。
注2可能性测度[15]除了满足以上条件外,还需满足Po(Paths(M))=1。
定义7[19](GPoCTL的语构)GPoCTL状态公式按如下规则定义:
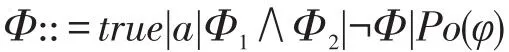
其中,a∈AP,φ是GPoCTL路径公式。
GPoCTL路径公式按如下规则定义:

其中,Φ、Φ1和Φ2是GPoCTL状态公式,且n∈N。
定义8[19](GPoCTL的语义)设M=(S,P,I,AP,L)是一个GPKS,a∈AP,s∈S,Φ和Ψ是GPoCTL状态公式,φ是GPoCTL路径公式。状态公式Φ的语义是一个模糊集||Φ||:S→[0,1],递归定义如下:

对于π∈Paths(M),路径公式φ的语义是一个模糊集||φ||:Paths(M)→[0,1],递归定义如下:

路径公式⋄Φ(“最终”)定义为⋄Φ=true⋃Φ,其语义为:

3 IGPoCTL与CTL表达能力的比较
首先定义了IGPoCTL,并给出IGPoCTL公式和CTL公式等价的定义,然后比较了IGPoCTL和CTL的表达能力。此外,还给出了IGPoCTL公式和CTL公式等价的另一种定义。
定义9(IGPoCTL的语构)IGPoCTL状态公式按照如下规则定义:
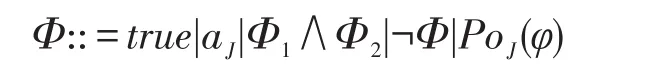
其中,a∈AP,φ是IGPoCTL路径公式,J⊆[0,1]是一个区间。
IGPoCTL路径公式按照如下规则定义:

其中,Φ、Φ1和Φ2是IGPoCTL状态公式,且n∈N。
定义10(IGPoCTL的语义)假设M=(S,P,I,AP,L)是一个GPKS,a∈AP,J⊆[0,1]是一个区间,s∈S,Φ1和Φ2是IGPoCTL状态公式,φ是IGPoCTL路径公式,π=s0s1s2…是M中的任意一条路径,对任意的i≥0,记π[i]=si,则状态公式的满足关系定义为:

路径公式的满足关系定义为:

3.1 IGPoCTL公式和CTL公式等价的定义
定义11设M是一个有限的GPKS,S是状态空间,Φ是IGPoCTL状态公式,则状态公式Φ的满足集为。若M是明确的,则SatM(Φ)也可以简记为Sat(Φ)。
定义12设Φ1和Φ2是两个IGPoCTL状态公式,如果对任意的有限GPKSM,都有Sat(Φ1)=Sat(Φ2),则称Φ1和Φ2是等价的,记作Φ1≡Φ2。
定义13设Φ是IGPoCTL状态公式,Ψ是CTL状态公式,如果对任意的有限GPKSM=(S,P,I,AP,L),都有SatM(Φ)=SatTS(M)(Ψ),则称Φ和Ψ是等价的,记作Φ≡Ψ。其中,TS(M)=(S,→,I′,AP,L′),∀s,s′∈S,s→s′当且仅当P(s,s′)>0;s∈I′当且仅当I(s)>0;∀a∈AP,a∈L′(s)当且仅当L(s,a)>0。明显地,PathsM(s)=PathsTS(M)(s),下面都会记作Paths(s)。
定义14 ENF形式的CTL状态公式Φ的长度记为[Φ],表示Φ中子公式的个数,定义如下:
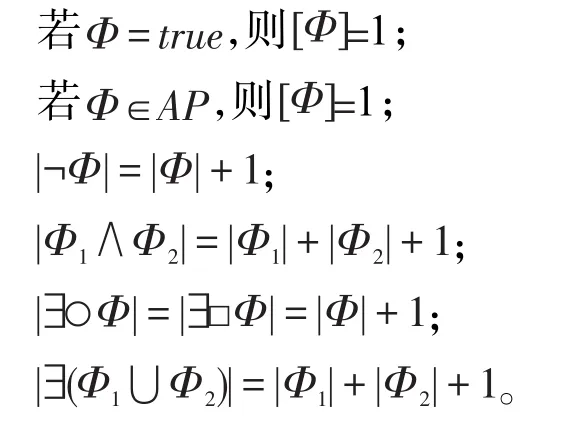
定理1设p∈[0,1],φ是任意的IGPoCTL路径公式,则Po<p(φ)≡¬Po≥p(φ)。
证明 设p∈[0,1],对任意的有限GPKSM=(S,P,I,AP,L),有:

3.2 CTL是IGPoCTL的子类
定理2[2]对任意的CTL公式,都存在一个ENF形式的CTL公式与其等价。
定理3对任意ENF形式的CTL公式Φ,都存在一个IGPoCTL公式Φ′与其等价,即Φ≡Φ′。
证明 设M是任意一个有限的GPKS,通过对公式Φ的长度进行归纳来证明:
(1)Φ=true,取Φ′=true。
(2)Φ=a,取Φ′=a>0。下证a≡a>0。因为sTS(M)a当且仅当a∈L′(s),当且仅当L(s,a)>0,当且仅当sMa>0,所以a≡a>0。
(3)Φ=∃φ,其中φ=○Φ|⋄Φ|□Φ|Φ1⋃Φ2,由归纳假设,存在IGPoCTL状态公式Φ1′和Φ2′,使得Φ1≡Φ1′,Φ2≡Φ2′。取Φ′=Po>0(φ′),其中,φ′=○Φ′|⋄Φ′|□Φ′|Φ1′⋃Φ2′。下证∃φ≡Po>0(φ′)。即需要证明SatTS(M)(∃φ)=SatM(Po>0(φ′))。其中,SatTS(M)(∃φ)={s|∃π∈Paths(s),πφ},SatM(Po>0(φ′))={s|Po(sφ′)>0},而Po(sφ′)=∨{PoMs(π)|π∈Paths(s),πφ′}。
假设s∈SatTS(M)(∃φ),则在TS(M)中,存在路径π,使得π∈Paths(s)且πφ。因为M是有限的,相应地,在M中有PoMs(π)>0和πφ′,从而∨{PoMs(π)|π∈Paths(s),πφ′}>0,即Po(sφ′)>0,则s∈SatM(Po>0(φ′)),所以SatTS(M)(∃φ)⊆SatM(Po>0(φ′))。
假设s∈SatM(Po>0(φ′)),则s满足Po(sφ′)>0,即∨{PoMs(π)|π∈Paths(s),πφ′}>0.因为M是有限的,则存在路径π,使得π∈Paths(s),PoMs(π)>0和πφ′。相应地,在TS(M)中,有π∈Paths(s)和πφ,则s∈SatTS(M)(∃φ),所以SatM(Po>0(φ′))⊆SatTS(M)(∃φ)。
综上所述,SatTS(M)(∃φ)=SatM(Po>0(φ′)),则∃φ≡Po>0(φ′)。
(4)Φ=Φ1∧Φ2。由归纳假设,存在IGPoCTL状态公式Φ1′和Φ2′,使得Φ1≡Φ1′,Φ2≡Φ2′。取Φ′=Φ1′∧Φ2′。下证Φ1∧Φ2≡Φ1′∧Φ2′。因为sTS(M)Φ1∧Φ2当且仅当sTS(M)Φ1且sTS(M)Φ2,当且仅当sMΦ1′且sMΦ2′,当且仅当sMΦ1′∧Φ2′,所以Φ1∧Φ2≡Φ1′∧Φ2′。
(5)Φ=¬Φ1。由归纳假设,存在IGPoCTL状态公式Φ1′,使得Φ1≡Φ1′,取Φ′=¬Φ1′。下证¬Φ1≡¬Φ1′。因为sTS(M)¬Φ1当且仅当sTS(M)Φ1,当且仅当sMΦ1′,当且仅当sM¬Φ1′,所以¬Φ1≡¬Φ1′。
综上所述,对任意ENF形式的CTL公式Φ,都存在一个IGPoCTL公式Φ′与其等价。
注3若CTL路径公式φ中还含有存在量词∃,则与其等价的IGPoCTL公式都需将其变为Po>0的形式。
例1如下ENF形式的CTL公式:¬(∃○(∃(a⋃∃○b))∧∃⋄a∧¬a),其中a,b∈AP,存在与其等价的IGPoCTL公式,具体如下:

由定理3,可得如下等价式(若CTL状态公式是Φ,则与其等价的IGPoCTL状态公式记作Φ′)。
命题1如下具有存在量词∃的CTL状态公式等价于相应的IGPoCTL状态公式:

命题2如下具有任意量词∀的CTL状态公式等价于相应的IGPoCTL状态公式:

注4在上述推论中,有的式子在无限的GPKS中不成立。下面举出命题2(1)的一个反例。假设命题2(1)对任意的无限GPKSM=(S,P,I,AP,L)都满足,即∀s∈S,要么s满足∀○Φ和Po=0(○¬Φ′),要么都不满足。取Φ=a∈AP。如图1,通过计算可得Po(s0○¬a>0)=∨{PoMs0(π)|π∈Paths(s0),π○¬a>0}=0,则s0∈SatM(Po=0(○¬a>0))。但是s0ts1s2…○¬a>0,则s0∉SatTS(M)(∀○a)。从而可得SatM(Po=0(○¬a>0))≠SatTS(M)(∀○a),即∀○a≢Po=0(○¬a>0)。
结合定理2和定理3,可得如下定理。
定理4对任意的CTL公式,都存在一个IGPoCTL公式与其等价。
定理4说明:CTL是IGPoCTL的子类。
3.3 CTL是IGPoCTL的一个真子类
定理5不存在CTL公式与IGPoCTL公式Po=1(○a>0)等价。
证明 假设存在CTL公式Φ,使得Φ≡Po=1(○a>0)。图2和图3是两个有限的GPKSM1和M2。对M1而言,Po(s0○a>0)=∨{Po
M1s0(π)|π○a>0}=Po(s0s1s3ω)=1;对M2而言,Po(s0○a>0)=Po(s0s1s3ω)=0.8。因此,s0∈SatM1(Po=1(○a>0)),而s0∉SatM2(Po=1(○a>0)),则可得:

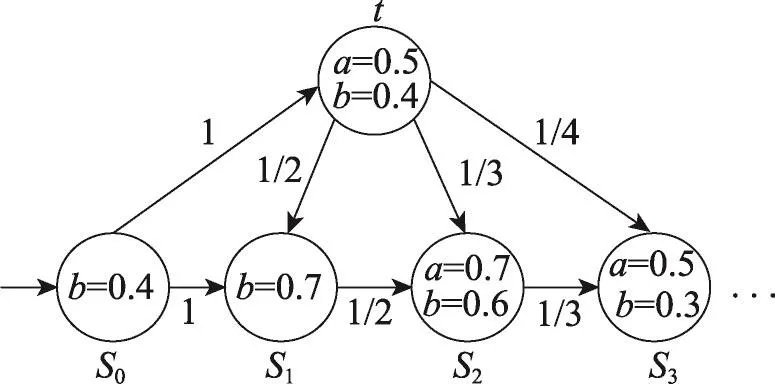
Fig.1 An infinite GPKSM图1 无限的GPKSM
因为Φ是一个CTL公式,且TS(M1)=TS(M2),则

但假设Φ≡Po=1(○a>0),即对任意的有限 GPKSM,都有SatTS(M)(Φ)=SatM(Po=1(○a>0))成立。则对M1,有SatTS(M1)(Φ)=SatM1(Po=1(○a>0));对M2,有SatTS(M2)(Φ)=SatM2(Po=1(○a>0))。结合等式(2),则有:
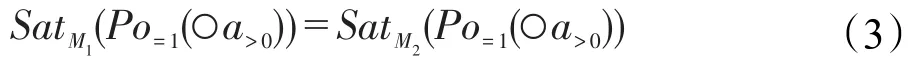

Fig.2 Afinite GPKSM1图2 有限的GPKSM1

Fig.3 Afinite GPKSM2图3 有限的GPKSM2
由上可知,等式(1)和等式(3)存在矛盾,故假设不成立,即不存在CTL公式与IGPoCTL公式Po=1(○a>0)等价。
由定理4和定理5可得:CTL是IGPoCTL的一个真子类,因为IGPoCTL是GPoCTL的一种简单分明化形式,则CTL可看作GPoCTL的一个真子类。
采用和定理5类似的证明方法可以得到如下定理。
定理6不存在CTL公式与IGPoCTL公式Po<1(○a>0)等价。
定理7不存在CTL公式与IGPoCTL公式Po=1(⋄a>0)等价。
定理8不存在CTL公式与IGPoCTL公式Po=1(□a>0)等价。
定理9不存在CTL公式与IGPoCTL公式Po<1(a>0⋃b>0)等价。
定理10不存在CTL公式与IGPoCTL公式a=1和a<1等价。
3.4 IGPoCTL公式和CTL公式等价的另一种定义
定义15设Φ是IGPoCTL状态公式,Ψ是CTL状态公式,α∈(0,1],如果对任意的有限GPKSM=(S,P,I,AP,L),都有SatM(Φ)=SatTSα(M)(Ψ),则称Φ和Ψ是α-等价的,记作Φ≡αΨ。其中,TSα(M)=(S,→α,Iα,AP,Lα),∀s,s′∈S,s→αs′当且仅当P(s,s′)≥α;s∈Iα当且仅当I(s)≥α;∀a∈AP,a∈Lα(s)当且仅当L(s,a)≥α。明显地,PathsM(s)=PathsTSα(M)(s),下面都会记作Paths(s)。
命题3设α∈(0,1],对任意的CTL公式都存在一个IGPoCTL公式与其α-等价。
例2对于例1中的CTL公式,存在与其α-等价的IGPoCTL公式,具体如下:

命题4设α∈(0,1],如下具有存在量词∃的CTL状态公式α-等价于相应的IGPoCTL状态公式:
命题6设α∈(0,1],不存在CTL公式与IGPoCTL公式a=0.5α-等价。
由命题3和命题6可得:设α∈(0,1],在α-等价的情况下,CTL是IGPoCTL的一个真子类。
注5若采用3.2节中的等价定义,根据定理3有∃φ≡Po>0(φ′)。可知:当某一事件的可能性大于0时,则与该事件相对应的事件存在。若采用1-等价,则会出现这种情况:当某一事件的可能性大于0时,并不意味着与该事件相对应的事件存在。例如:对于图3,有Po(s0○a=1)=0<1,则s0Po=1(○a=1)。根据命题 4(1),若取α=1(即采用1-等价),则能推出s0∃○a。但显然有s0∃○a。

命题5设α∈(0,1],如下具有任意量词∀的CTL状态公式α-等价于相应的IGPoCTL状态公式:

4 总结
本文定义了IGPoCTL,给出了IGPoCTL公式和CTL公式等价的定义,证明了对任意的CTL公式都存在与其等价的IGPoCTL公式,但对任意的IGPoCTL公式不一定都存在与其等价的CTL公式,即CTL是IGPoCTL的一个真子类。最后给出了IGPoCTL公式和CTL公式α-等价的定义,并得出了更一般的结果。本文结论进一步揭示了GPoCTL的表达能力。
[1]Clark E M,Grumberg O,Peled D.Model checking[M].Cambridge,USA:MIT Press,1999.
[2]Baier C,Katoen J P.Principles of model checking[M].Cambridge,USA:MIT Press,2008.
[3]Clark E M,Grumberg O,Long D E.Model checking and abstraction[J].ACM Transactions on Programming Languages and Systems,1994,16(5):1512-1542.
[4]Lin Huimin,Zhang Wenhui.Model checking:theories,techniques and applications[J].Acta Electronica Sinica,2002,30(12A):1907-1912.
[5]Cao Yongzhi,Ying Mingsheng.Observability and decentralized control of fuzzy discrete event systems[J].IEEE Transactions on Fuzzy Systems,2006,14(2):202-216.
[6]Clarke E M,Emerson E A,Sistla A P.Automatic verification of finite state concurrent systems using temporal logic specifications[J].ACM Transactions on Programming Languages and Systems,1986,8(2):244-263.
[7]Hart S,Sharir M.Probabilistic propositional temporal logics[J].Information and Control,1986,70(2/3):97-155.
[8]Fischer D,Grädel E,Kaiser Ł.Model checking games for the quantitativeµ-calculus[J].Theory of Computing Systems,2010,47(3):696-719.
[9]Chechik M,Devereux B,Easterbrook S,et al.Multi-valued symbolic model-checking[J].ACM Transactions on Software Engineering and Methodology,2003,12(4):371-408.
[10]Lei Lihui,Duan Zhenhua.An extended deterministic finite automata based on possibility measure[J].Journal of Software,2007,18(12):2980-2990.
[11]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[12]Klir G J,Folger T A.Fuzzy sets,uncertainty and information[M].Englewood Cliffs,USA:Prentice Hall,1988.
[13]Dubois D J.Fuzzy sets and systems:theory and application[M].New York:Academic Press,1980.
[14]Li Yongming.Analysis of fuzzy systems[M].Beijing:Science Press,2005.
[15]Li Yongming,Li Lijun.Model checking of linear-time properties based on possibility measure[J].IEEE Transactions on Fuzzy Systems,2013,21(5):842-854.
[16]Li Yongming,Li Yali,Ma Zhanyou.Computation tree logic model checking based on possibility measures[J].Fuzzy Sets and Systems,2015,262:44-59.
[17]Xue Yan,Lei Hongxuan,Li Yongming.Computation tree logic based on possibility measures[J].Computer Engineering and Science,2011,33(9):70-75.
[18]Li Yongming.Two methods for possibilistic linear temporal logic model checking[J].Journal of Shaanxi Normal Uni-versity:Natural Science Edition,2014,42(6):21-25.
[19]Li Yongming,Ma Zhanyou.Quantitative computation tree logic model checking based on generalized possibility measures[J].IEEE Transactions on Fuzzy Systems,2015,23(6):2034-2047.
附中文参考文献:
[4]林惠民,张文辉.模型检测:理论,方法与应用[J].电子学报,2002,30(12A):1907-1912.
[10]雷丽晖,段振华.一种基于扩展有限自动机验证组合Web服务的方法[J].软件学报,2007,18(12):2980-2990.
[14]李永明.模糊系统分析[M].北京:科学出版社,2005.
[17]薛艳,雷红轩,李永明.基于可能性测度的计算树逻辑[J].计算机工程与科学,2011,33(9):70-75.
[18]李永明.可能LTL模型检测的两种方法[J].陕西师范大学学报:自然科学版,2014,42(6):21-25.
Relationship Between Generalized Possibilistic Computation Tree Logic and Computation Tree Logic*
LI Dan,LI Yongming+
College of Computer Science,Shaanxi Normal University,Xi'an 710119,China


A
TP301.2
+Corresponding author:E-mail:liyongm@snnu.edu.cn
LI Dan,LI Yongming.Relationship between generalized possibilistic computation tree logic and computation tree logic.Journal of Frontiers of Computer Science and Technology,2017,11(10):1681-1688.
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2017/11(10)-1681-08
10.3778/j.issn.1673-9418.1607030
E-mail:fcst@vip.163.com
http://www.ceaj.org
Tel:+86-10-89056056
*The National Natural Science Foundation of China under Grant Nos.11271237,61228305(国家自然科学基金).
Received 2016-06,Accepted 2016-08.
CNKI网络优先出版:2016-08-19,http://www.cnki.net/kcms/detail/11.5602.TP.20160819.0932.004.html
LI Dan was born in 1991.She is an M.S.candidate at Shaanxi Normal University.Her research interest is model checking.
李丹(1991—),女,山西平陆人,陕西师范大学硕士研究生,主要研究领域为模型检测。
LI Yongming was born in 1966.He received the Ph.D.degree from Sichuan University in 1996.Now he is a professor and Ph.D.supervisor at Shaanxi Normal University,and the senior member of CCF.His research interests include intelligent computing,fuzzy system analysis,quantum logic and quantum computing,etc.
李永明(1966—),男,陕西大荔人,1996年于四川大学获得博士学位,1999年于西北工业大学博士后流动站出站,现为陕西师范大学教授、博士生导师,CCF高级会员,主要研究领域为计算智能,模糊系统分析,量子计算与量子逻辑等。

