高维相关性缺失数据的分块填补算法研究*

杨 杰，杨 虎，王鲁滨，金 鑫，郭 华，于亮亮

1.中央财经大学 信息学院，北京 100081

2.国网荆州供电公司 信通分公司，湖北 荆州 434000

3.国网辽宁省电力有限公司 信息通信分公司，沈阳 110000

高维相关性缺失数据的分块填补算法研究*

杨 杰1+，杨 虎1，王鲁滨1，金 鑫1，郭 华2，于亮亮3

1.中央财经大学 信息学院，北京 100081

2.国网荆州供电公司 信通分公司，湖北 荆州 434000

3.国网辽宁省电力有限公司 信息通信分公司，沈阳 110000

Abstract:This paper studies the method of filling the high dimensional correlation missing data,and proposes a new imputation algorithm based on data block.The key idea of the algorithm is to consider the correlation between variables when filling missing data,and only use the data correlated with the missing data to fill,thereby reducing imputation effects of the missing data caused by the irrelevant data,and improving the accuracy of data imputation.At the same time,the proposed imputation algorithm can be implemented in a parallel way,so that it performs efficiently to fill the high dimensional missing data.In order to divide the missing data with unknown information about blocks into several blocks,this paper proposes a block algorithm based onk-means clustering.Simulation research and application show that the proposed imputation algorithm is more effective and accurate to handle themissing for the correlation high dimensional data with considering variables'block relationship than others with not.

Key words:high dimensional correlation data;missing data;block imputation algorithm

研究了高维相关性缺失数据的填补方法，提出了分块填补算法。该算法核心思想是：在填补数据的过程中会考虑变量之间的相互关系，仅利用与待填补数据有相关性的数据进行填补，从而降低不相关数据对缺失数据填补的影响，提高数据填补的准确度。同时，该算法能够并行处理缺失数据，从而提高数据填补效率，对于高维缺失数据的填补有重要意义。为了对分块情况未知的缺失数据进行分块，提出了基于k-means聚类的分块算法。大量的仿真实验和基于真实数据集的实验表明，对于相关性数据，分块填补算法能够有效地利用相关信息进行填补，从而提高数据填补准确度。

高维相关性数据；缺失数据；分块填补算法

1 引言

随着大数据相关理论和技术的发展，大数据在电力、医疗、金融、交通、电信等方面有了广泛应用。由于大数据的数据量非常巨大，在采集和存储过程中，不可避免地出现数据缺失的现象。缺失数据往往含有重要的信息和价值，对缺失数据处理不当，会对数据分析结果产生巨大影响，甚至会严重影响数据的客观性和研究结论的正确性[1]。因此，如何对大数据中的缺失数据进行填补是一个重要的研究内容。

传统的数据填补方法包括多重插补[2]、基于回归的填补算法[3]、基于关联规则的填补算法[4]、基于决策树的填补算法[5]、基于K近邻的填补算法[6]、基于贝叶斯的填补算法[7]、基于聚类的填补算法[8]。更进一步，可以结合两种或两种以上的算法对缺失数据进行填补，如基于关联规则和K近邻算法的填补算法[9]、基于关联规则和聚类的填补算法[10]、基于聚类和最近邻算法的填补算法[11]。

研究表明，传统的数据填补算法对于小数据集填补的确有一定的准确性，但面对大数据集，往往填补效果不佳。针对这一问题，相关学者已经进行了一些缺失大数据填补方法的研究。陈肇强等人[12]运用互联网中海量信息对缺失大数据进行填补，提出了基于上下文感知实体排序的缺失数据修复方法；金连等人[13]结合Map-Reduce的并行化特点，提出来了基于Map-Reduce的大数据缺失值填补算法，提高了大数据的填补效率；冷泳林等人[14]同时结合聚类算法和并行处理对缺失大数据进行填补；赵飞等人[15]针对高速流数据中的缺失值，提出了基于最小计数/频率概要的缺失值填补方法。

传统的针对一般缺失数据的填补方法和现有的针对缺失大数据的填补方法只考虑了观测样本之间的关系，而忽略了变量之间的关系，而变量之间的相关性往往会影响数据的填补效果。例如，身高与体重之间有相关关系，而与智力没有直接关系，如果将智力这个变量的信息用于填补身高数据的缺失，则会对数据填补结果造成一定的影响。在高维大数据情形下，不相关变量会越来越多，对数据填补准确性的影响也会越来越大。

一些研究已经注意到了这些问题，它们主要通过变量约简的方法，剔除掉不相关的变量，来提高数据填补的效果。例如，陈志奎等人[16]通过变量约简，将变量分成重要变量和非重要变量，分别采用不同的填补算法进行填补。刘春英[17]通过考虑变量之间的依赖关系而对变量进行区分，分别进行填补。

为了处理缺失高维大数据，本文创新性地提出了一种针对高维相关性缺失数据的分块填补算法。本文算法首先通过变量之间的相关性，将原始数据集进行纵向分割，形成众多的低维子数据集；然后利用数据填补算法，分别对每个分块进行填补。本文算法最大的优点在于降低了不相关变量对填补结果的影响，从而能够提高填补准确度；同时本文算法能够以并行的方式对高维缺失大数据进行填补，不仅能提高缺失填补的精度，还能降低数据填补的计算时间。

本文组织结构如下：第2章给出了分块填补算法及其相关定义，从理论上证明了分块填补能够提高准确性，并提出了基于k-means的数据分块算法；第3章给出分块填补算法的具体步骤；第4章通过模拟仿真说明本文填补算法处理高维缺失大数据的准确度和效率；第5章将分块填补算法应用于基因测序数据，说明处理真实数据的能力；第6章总结全文。

2 相关理论

2.1 相关定义

定义1（缺失数据集）含缺失数据的数据集称为缺失数据集。为了方便描述，本文利用粗糙集理论中信息系统的概念来进行描述。一个信息系统由一个四元组来表示：

其中，U={x(1),x(2),…,x(n)}表示对象集，n为对象的个数；A={a1,a2,…,ap}表示变量集，p表示变量的个数；V表示每个变量的值域；f是U×A到V的一个映射，即：

当信息系统S至少存在一组(i,j)使得，其中i=1,2,…,|U|,j=1,2,…,|A|,则称该信息系统为不完备信息系统，即缺失数据集。

定义2（遗失数据集）遗失数据集是对缺失数据的描述，缺失数据集S的遗失数据集MI定义为：

其中，i=1,2,…,|U|,j=1,2,…,|A|。

定义3（变量相关性）变量相关性表示变量之间的相关程度或者依赖程度。本文用r(ai,aj)来表示变量ai和aj之间的相关性，其中ai,aj∈A,0≤r(ai,aj)≤ 1,r(ai,aj)越大，表示ai和aj相关性越高。r(ai,aj)=0,表示ai和aj完全无关；r(ai,aj)=1,表示ai和aj完全相关。

关于不同变量之间相关性的定义，在不同的领域都有不同的定义。由于相关性不是本文重点讨论的内容，本文仅采用归纳的研究方法对相关性进行归纳描述，不做深入的讨论和研究。在实际应用中，相关系数、关联规则、依赖度等均可以用来表示变量之间的相关性。

（1）相关系数

相关系数可以刻画两个变量之间的变动关系，常用于数学、统计等领域。相关系数一般用ρ表示，值域为[-1,1]。ρ的绝对值越大，表示相关性越高，反之越低。

（2）关联规则

关联规则在数据挖掘领域中用来表示不同事务之间的相关性，其最大的特点就是能够找出表面上不易发现，内在却存在的相关性。例如一个人购物篮里面物品之间的相关性就可以用关联规则来描述。

（3）依赖度

依赖度是粗糙集理论中的一个概念，用来表示一个变量对另外一个变量的依赖程度，依赖度越高，意味着其相关性也越高。

定义4（相关变量集）相关变量集RA是A的一个子集，设0≤∂≤1为变量相关性阈值，则RA定义如下：

其中，ai,aj∈RA,i≠j。

定理1变量集A与相关变量集RA的关系为为变量集分块个数。

证明 由定义4可知，RA是A的子集，且RAi⋂RAj=∅ ,i≠j。因此，对任意的i∈[1,K]，RAi是A的真子集，从而

定义5（分块数据集）根据RA可以将S分成多个子数据集，每个子数据集称为一个分块数据集，分块数据集RS定义为:

RS=(U,RA,V,f)

定理2数据集S与分块数据集RS的关系为，K为数据集分块个数。

定义6（分块填补算法）数据填补算法可以统一定义为一种映射函数h:S→S′。其中S为缺失数据集，S′=(U′,A,V,f′)为经过填补后的完备数据集。

根据填补算法依赖的变量的不同，可以将填补算法分成3类：单变量依赖填补算法、全变量依赖填补算法和分块填补算法。

设(i,j)∈MI(S)，为的填补值。

（1）单变量依赖填补算法是指对缺失值的填补只与当前的缺失变量有关，而与其他变量值无关，如均值填补、众数填补等，定义如下：

（2）全变量依赖填补算法是指对缺失值的填补与所有的变量都有关，如KNN填补算法、回归填补算法等，其定义如下：

（3）分块填补算法是指对缺失值的填补只与部分变量相关，定义如下：

其中，RAj为变量aj所在的相关变量集。

2.2 分块填补的性质

假设存在一个高维数据集A∈Rn×p，n≪p，假定A满足以下的假设。

（1）可分性。A可以按列分成K个分块，即：

（2）独立性。各块之间相互独立，即有：

（3）线性关系。各变量之间有近似的线性相关关系，即有：

其中，ui为白噪声，i∈[1,p]；A*=Aai,表示不包含第i个变量。

（4）数据随机缺失。

同时，本文用均方根误差（root mean square error，RMSE）来评价数据填补的准确程度，RMSE定义如下：

其中，N为缺失数据的个数；为缺失数据xi的填补估计值；ei2表示残差的平方。RMSE越小，表示填补准确度越高，反之越低。

根据上述假设，可得到定理3。

定理3在满足4个假设条件的前提下，分块填补的精度高于不分块填补的准确性。

证明（1）由假设（3），各变量之间存在近似的线性相关关系，因此可以采用最小二乘的方法来对缺失数据的填补值进行估计，用表示ai的最小二乘估计值。对ai的估计有两种情况：一种是利用全部的信息进行估计，即不分块填补；另一种是仅利用最相关信息进行估计，即分块填补。

情形1ai的不分块估计值：

由假设（1）可知，A是按列可分的，因此式（2）可以变换为：

则ai不分块估计的残差平方和为：

情形2ai的分块估计值为：

则ai的分块估计的残差平方和为：

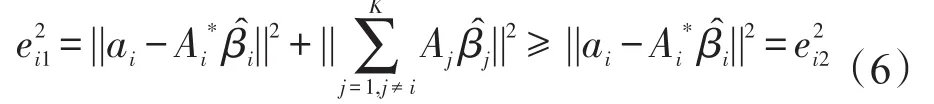
用aim表示变量ai上由缺失数据组成的向量，由假设（4）可知，由于缺失方式为随机缺失，aim也满足假设（2）的独立性条件。因此，变量ai上缺失数据在不分块估计和分块估计上的残差平方和（分别用和表示）也满足:

（3）根据RMSE的定义，不分块填补和分块填补两种方式下的填补精度（用RMSEnb和RMSEb来表示）分别为：

结合式（7）可得，RMSEnb≥RMSEb,即分块填补的精度高于不分块填补的精度。

2.3 分块方法

根据对数据集的理解情况，可以分为分块已知和分块未知两种情况进行讨论。

2.3.1 分块已知的情况

对于一个分块信息已知的情况，直接根据已知分块信息进行分块即可。分块已知的情况一般出现在变量较少，且对变量的含义有明确认识的情况。

2.3.2 分块未知的情况

实际中，大多数数据集都是未知分块的。特别是对于高维数据或者对变量含义不了解的数据，难以识别其中的分块信息。针对分块未知的情况，本文基于k-means算法，通过改进数据缺失情况下的距离度量方式，从而实现了对缺失数据进行分块，本文称之为KMB算法（k-means block algorithm）。

（1）k-means算法

k-means是一种经典的聚类算法。给定数据集A∈Rn×p。k-means算法步骤如下所示。

算法1k-means算法

输入：数据集A，聚类个数K。

输出：每个对象a(i)所在的聚类。

步骤1随机选取K个聚类中心为u1,u2,…,uK∈Rp。

步骤2迭代直至收敛。

对A中的每一个对象a(i)，计算其所属的聚类：

对于每一个类j，更新类的中心：

（2）基于k-means的分块算法

结合k-means算法的思想，本文提出了对变量进行分块的KMB算法。在描述算法之前，需要解决以下几个问题。

第一，聚类算法可以分为Q型聚类和R型聚类。Q型聚类是指对数据对象进行聚类，k-means算法就是一种Q型聚类算法。R型聚类是指对变量进行聚类。为了能够使用k-means算法对变量进行聚类，首先需要对数据集进行转置得到AT∈Rp×n，然后对A′进行聚类。

第二，k-means算法对高维数据的处理效果不佳，存在一定的局限性。本文中，当样本量n较小时，转置后的AT是一个低维的数据集，则使用k-means算法进行聚类不存在局限性问题。当n比较大时，转置后的AT仍然是一个高维的数据集，此时使用k-means算法进行聚类存在一定的局限性。为了解决这一问题，本文采用Witten等人[18]提出的稀疏性k-means算法（sparsek-means clustering）进行变量选择。其核心思想是约束目标函数中变量的权重，使得权重较小的变量不参与聚类，而保留权重较大的变量，从而实现变量选择，其目标函数定义如下所示：

其中，w为变量的权重向量；wv表示第v个变量的权重系数；s为调整参数。

这样，通过变量选择解决了数据量很大时kmeans算法的局限性问题。

第三，经典k-means算法一般采用欧式距离来计算距离，在数据缺失的条件下，难以计算欧式距离。本文采用Hathaway等人[19]提出的计算缺失数据的距离的方法。包含缺失对象a(i)和a(j)之间的距离定义为：

第四，经典k-means算法一般采用算数平均的方法来更新聚类的中心，但在数据缺失的情况下，此方法不再可行。同样借鉴Hathaway等人的思想，本文提出了在缺失情况下更新聚类中心的方法。设第j个聚类中有s个对象{a(1),a(2),…,a(s)}，且包含缺失，则类中心uj在第i个变量上的取值定义为：

解决了以上问题，下面给出具体的KMB算法步骤，如下所示。

算法2KMB算法

输入：数据集A，聚类个数K。

输出：分块数据集。

步骤1对A进行转置，得到AT。

步骤2随机选取K个聚类中心点为u1,u2,…,uK∈Rn。

步骤3迭代直至收敛。

对AT中的每一个对象a(i),计算其所属的聚类：

对于每一个类j，按照本文定义的方法更新聚类的中心：

步骤4转置聚类完成的数据集，得到A1。

步骤5根据聚类结果分割数据集A1,得到多个分块数据集。

3 分块填补算法

分块填补算法是根据数据集的特征，通过对数据集进行分块而形成的一种缺失数据填补算法。其最大的特征是适用的填补算法范围广，凡是依赖于其他变量的数据填补算法均适用于分块填补的方案，统称此类算法为宿主算法。分块填补算法步骤见算法3。

算法3分块填补算法

输入：缺失数据集S=(U,A,V,f)。

输出：完备数据集S′=(U′,A,V,f′)。

步骤1确定分块。如果分块已知，则直接进行分块；否则应用KMB算法（算法2）进行分块，得到分块信息。

步骤2根据分块信息，对缺失数据集S进行分割，得到K个子缺失数据集RSi=(U,Ai,V,f),i=1,2,…,K。

步骤3对于每一个子缺失数据集，使用宿主填补算法进行填补，得到完备的子数据集Si=(U′,Ai,V,f′),i=1,2,…,K。

步骤4合并完备的子数据集Si，得到完备数据集S′=(U′,A,V,f′)。

由算法3可知，分块填补算法具有以下特点：

（1）缺失数据集是可分的，即可以分成多个块内相关性高，块间相关性低的数据分块。一方面，如果缺失数据集的所有变量之间都具有很高的相关性，那么对数据集进行分割，反而会破坏这种强的相关性，不利于数据填补。另一方面，如果数据集的变量之间均存在较弱的相关性，划分之后，变量之间的相关性仍然很低，也不利于数据填补。

（2）适用的宿主填补算法广，即大部分传统的填补算法均可作为本文提出的分块填补算法的宿主算法，适用范围广。具体来讲，除均值填补和众数填补等少数不依赖变量的填补算法外，都适合分块填补算法。

（3）并行填补，提高填补效率。通过对原始数据集进行分块，对每个分块可以采用并行的方式进行填补，总的填补计算时间降为max(t1,t2,…,tK)，其中K为分块个数，tK表示第K个分块的填补时间。当数据集的维度和数据量很大时，分块填补能够明显降低填补计算时间。

4 仿真实验

4.1 实验环境

（1）实验数据生成

为了评价分块填补算法对存在分块的高维相关性缺失数据在分块已知和分块未知两种情况下的填补效果，本文仿真生成了样本量固定为n=100,变量个数分别为p=100,p=200和p=400的3个仿真数据集，来检验对于不同变量个数的数据集，分块填补算法的效果。每个数据集的生成方式如下：首先确定数据集的分块数为K块；然后对于每个分块Ki，它有pi个变量，数据由多元正态分布N(ui,Σi)产生，其中ui是pi维期望向量，Σi是pi×pi的协方差矩阵。为了保证不同块之间有一定的差异，使不同分块的期望向量之间存在一定的差异；最后将各个分块合并形成仿真数据集，并重复100次。

（2）实验平台

本实验采用Matlab 2011B作为实验平台，操作系统是Windows8.1专业版，Intel®Pentium®CPU P6200 2.13 GHz，2 GB 内存，320 GB硬盘。

4.2 实验设置

（1）实验方法

采用随机缺失的方法，根据设定的缺失率，随机地置空仿真数据集，得到包含缺失的数据集。分别使用宿主填补算法KNN（K近邻）填补算法和REGRESS（线性回归）填补算法对缺失数据进行分块填补，并与不分块的填补算法进行对比，比较它们的填补准确度和填补计算时间。每种算法均用于分析100个模拟生成的数据，并计算平均填补准确度和平均填补计算时间。

（2）评价指标

根据数据类型的不同，对填补准确度的衡量方法也不同。对于数值型数据，使用均方根误差（RMSE）来衡量填补准确度，其定义见式（1）。

对于离散性数据，采用填补准确率（Precise）来衡量，即填补正确的数据记录数占整个缺失数据的比例。Precise越大，填补精度越高。其定义为：

（3）实验设计

根据实验目的不同，本文总共设计了两个实验。

实验1假定分块已知，即按照仿真数据产生时设定的分块对各数据集进行分块，然后使用K近邻（KNN）填补算法和回归（REGRESS）填补算法分别进行填补，将结果与不分块的情况进行比较，以验证在数据存在分块的情况下，本文提出的分块填补算法是否优于不分块填补算法。

实验2假定分块未知，即实验前只知道数据存在分块，但并不知道具体的分块情况。首先使用本文提出的分块算法KMB（算法2）对数据进行分块，然后用KNN填补算法和REGRESS填补算法分别进行填补；最后比较和验证在数据存在分块但分块未知的情况下，本文提出的分块填补算法是否优于不分块填补算法，并对KMB算法进行评价。

4.3 实验结果

（1）实验1结果分析

按10%、20%、30%、40%和50%缺失比例随机缺失3个变量个数不同的数据集，然后在分块和不分块的情形下，分别采用KNN填补算法和REGRESS填补算法进行填补。各算法填补的均方根误差和平均填补时间分别由表1和表2给出。

表1表明，已知分块的情况下，在相同的缺失率水平下，同一宿主算法的分块填补算法的均方根误差均大于其不分块填补算法，即分块填补算法的填补准确度高于不分块填补算法，这在3个变量个数不同的数据集中均成立；对于任意的填补算法，填补的准确度均随缺失率的上升而下降。以上结果表明，在数据存在分块的情况下，本文提出的分块填补算法能够提高填补准确度。

表2是各算法对不同数据集在不同缺失率情况下进行填补的平均时间比较。可以得到，对于相同的数据集，各算法的平均填补时间均随缺失率的上升而上升；对于相同数据集和相同缺失率，同一宿主算法分块填补的平均填补时间小于不分块填补；同一算法在相同缺失率水平下，平均填补时间随变量个数的增加而增加。以上表明，本文提出的分块填补算法能够有效降低数据填补时间。

Table 1 RMSE of different imputation algorithms in different simulation datasets表1 不同模拟数据集上各个填补算法的均方根误差

Table 2 Average imputation time of different imputation algorithms in different simulation datasets表2 不同模拟数据集上各个填补算法的平均填补时间

（2）实验2结果分析

实验2采用仿真生成的(n=100,p=100)和(n=100,p=1 000)两个数据集进行实验，分别代表变量个数较小和变量个数较大的两种情况。与实验1不同的是，实验前假定并不知道具体分块情况，而是通过KMB算法（算法2）来自动进行分块，然后使用KNN填补算法和REGRESS填补算法进行填补。由于并不知道具体的分块数，因而无法确定KMB算法中的K值。本文通过设定一个较大的K值(MAXK),然后从K=1到K=MAXK循环调用KMB算法进行分块，同时对每个分块使用KNN填补算法和REGRESS填补算法进行填补，然后观察比较在K的不同取值下，填补结果的RMSE与K的关系。

情形1变量较少的情况

在仿真数据集(n=100,p=100)下，设定MAXK=25，相关结果如图1所示。

Fig.1 Results of case 1(n=100,p=100)图1 情形1(n=100,p=100)的实验结果

图1（a）描述了在不同缺失率下，KNN填补算法的RMSE与K的关系。由图1（a）可以看出，随着K的增加，RMSE先减小，后增加，整个图形呈“U”型，在K=5左右达到最小值。从图1（a）中可以得到以下结论：

（1）在分块数K相同时，RMSE随缺失率的增加而增加，意味着在分块未知的情况下，填补准确度仍随着缺失率的上升而下降。

（2）关于“U”型形状的解释。当K=1时，为不分块填补，填补结果有较大的均方根误差，因为缺失数据中含有较多的不相关信息参与了缺失值的填补；随着K的逐渐增加，同一分块中的不相关变量被分割出去，相关变量的比例上升，即同一分块的相关性相对上升，从而使得填补的准确性上升；当K增加到一定程度之后，同一分块的变量之间已经具有较多的相关变量，同时具有较低的不相关变量；当K进一步增加，同一分块的变量个数必然下降，致使部分相关性高的变量被分割出去，即分块内本身存在的强相关性此时也被破坏，从而导致了填补准确度下降；当K很大时，分块填补的准确度甚至会超过不分块填补的准确度，因为此时产生了大量相关性弱的分块。

（3）分块未知的情况下，以及在K较小的情况下，KMB算法能够找到合适的分块来提高填补准确度，说明KMB算法能够很好地对分块未知的数据进行分块。

图1（b）描述了在不同缺失率下，KNN算法平均填补时间随K的变动情况。可以看出，随K的增加，各缺失率下，平均填补时间呈下降趋势，当K增加到一定程度时，平均填补时间保持平稳。这是因为此时每个分块都很小，不再是影响填补时间的主要因素。同时，对于相同的K，平均填补时间随着缺失率的上升而上升。

图1（c）和（d）分别是REGRESS填补算法在数据集1上填补的均方根误差和平均填补时间随分块数K的变动情况。与KNN算法相比，有类似的结论，这里不再赘述。

情形2变量较多的情况

在仿真数据集(n=100,p=1 000)下，设定MAXK=100,相关结果如图2所示。

从图2（a）中可以看出，基于KNN的分块填补算法在变量个数较多的情况下RMSE与K仍具有明 显的“U”型特征，填补的均方根误差随缺失率上升而上升。

从图2（b）中可以看出，填补时间随K的增加而减少，随缺失率的上升而上升。说明KNN填补算法对不同的样本量具有良好的稳定性。

Fig.2 Results of case 2(n=100,p=1 000)图2 情形2(n=100,p=1 000)的实验结果

从图2（c）中可以看出，在变量很多的情况下，REGRESS算法的均方根误差与分块数的“U”型特征不是十分明显，均方根误差先随着分块数的增加逐步下降，然后逐步保持在较低的水平，当K=40左右才有微弱的上升趋势。主要是因为K值还不够大，总的变量个数又很多，所以各个分块还有足够的相关变量用于缺失数据的填补。

从图2（d）中可以看出，平均填补时间随K的增加仍然有逐步减少，然后保持在较低水平的规律。

综上，仿真实验的结果表明了对于相关性数据，在已知分块的情况下，分块填补的准确度高于不分块填补，同时可以降低填补时间；在分块未知的情况下，也可以通过KMB算法（算法2）找到分块，从而提高数据填补的准确度。仿真实验还揭示了分块填补的准确度随分块个数的增加，先增加后降低的规律；当分块数足够大时，会因为不正确的分块导致分块填补的准确度低于不分块填补的情况出现。

5 真实数据分析

为了评价分块填补算法在电力、医疗等真实数据上的填补效果，本文将分块填补算法应用到白血病的基因表达数据集leukemia上。该数据集来源于麻省理工学院和哈佛大学的生物医学和基因组研究中心Broad Institute，含有461个变量，1 394个样本。因为数据分块未知，先用KMB算法（算法2）进行分块，然后采用KNN填补算法进行填补，实验结果如图3和图4所示。

Fig.3 Relationship betweenRMSEandK图3 均方根误差与分块数K的关系

Fig.4 Relationship between average imputation time andK图4 平均填补时间与分块数K的关系

从图3中可以看出，采用不分块的方式进行填补(K=1)有较高的均方根误差，随着分块数的增加，均方根误差逐步减小，在K=10左右达到最低，然后波动上升，整个图形呈“U”型。同时，在分块数K相同时，RMSE随着缺失率的提高而上升，即填补准确度随缺失率上升而下降。综上可知，使用分块填补算法在真实数据集中也能够提高填补准确度。

由图4可知，相同缺失率下，平均填补时间随着分块数的增加而减少；相同分块数下，平均填补时间随缺失率上升而下降。

综上可知，真实数据中的结果与仿真实验得到的结论一致，进一步说明了分块填补算法能够提高填补准确度和降低填补时间。

6 结束语

本文针对高维相关性数据提出了基于变量分块的分块填补算法，有助于解决现实中电力、医疗等行业的大数据缺失填补问题。在分块已知的情况下，仿真实验表明分块填补能够提高数据填补的准确度和降低数据填补的计算时间。在分块未知的情况下，本文首先利用改进的k-means算法进行分块，然后再分别对各分块进行填补。仿真实验和真实数据分析结果表明，分块未知情况下分块填补同样可以提高填补准确度和降低数据填补的计算时间。同时实验表明，填补准确度随分块数的增加有先增加再减少的规律，即不同的分块数对填补准确度的提高程度不同。如何确定最优的分块数使得能够最大程度地提高分块填补算法的填补准确度是进一步研究的方向。

[1]Nakagawa S,Freckleton R P.Missing inaction:the dangers of ignoring missing data[J].Trends in Ecology and Evolution,2008,23(11):592-596.

[2]Rubin D B.Multiple imputation in sample surveys—a phenomenological Byesian approach to nonresponse[M]//Survey Research Methodology Section.Washington:American StatisticalAssociation,1978:20-34.

[3]Bello A L.Imputation techniques in regression analysis:looking closely at their implementation[J].Computational Statistics and DataAnalysis,1995,20(1):45-57.

[4]Shen J J,Chang C C,Li Y C.Combined association rules for dealing with missing values[J].Journal of Information Science,2007,33(4):468-480.

[5]Vateekul P,Sarinnapakorn K.Tree-based approach to missing data imputation[C]//Proceedings of the 2009 International Conference on Data Mining Workshops,Miami,USA,Dec 6,2009.Washington:IEEE Computer Society,2009:70-75.

[6]Zhang Sunli,Yang Huizhong.Missing data completion based on an improvedK-neighbor algorithm[J].Computers and Applied Chemistry,2015,32(12):1499-1502.

[7]Zou Wei,Wang Huijin.EM algorithm to implement missing values based on naive Bayesian[J].Microcomputer&Its Applications,2011,30(16):75-77.

[8]Wu Sen,Feng Xiaodong,Shan Zhiguang.Missing data imputation approach based on incomplete data clustering[J].Chinese Journal of Computers,2012,35(8):1726-1738.

[9]Wang Fengmei,Hu Lixia.A missing data imputation method based on neighbor rules[J].Computer Engineering,2012,38(21):53-55.

[10]Fang Kuangnan,Xie Bangchang.Research on dealing with missing data based on clustering and association rule[J].Statistical Research,2011,28(2):87-92.

[11]Zhang Chi,Feng Hongcai,Jin Kai,et al.Nearest neighbor filling algorithm for missing data based on cluster analysis[J].ComputerApplications and Software,2014,31(5):282-284.

[12]Chen Zhaoqiang,Li Jiajun,Jiang Chuan,et al.A contextaware entity ranking method for Web-based data imputation[J].Chinese Journal of Computers,2015,38(9):1755-1766.

[13]Jin Lian,Wang Hongzhi,Huang Shenbing,et al.Missing value imputation in big data based on Map-Reduce[J].Journal of Computer Research and Development,2013,50(S1):312-321.

[14]Leng Yonglin,Chen Zhikui,Zhang Qingchen,et al.Distributed clustering and filling algorithm of incomplete big data[J].Computer Engineering,2015,41(5):19-25.

[15]Zhao Fei,Liu Qizhi,Zhang Yan,et al.Fill absent values in massive domain data stream[J].Journal of Nanjing University:Natural Sciences,2011,47(1):32-39.

[16]Chen Zhikui,Yang Yingda,Zhang Qingchen,et al.Novel algorithm for filling incomplete data of Internet of things based on attribute reduction[J].Computer Engineering and Design,2013,34(2):418-422.

[17]Liu Chunying.A sequential filling algorithm for missing values based on attribute dependency[J].Computer Applications and Software,2013,30(9):215-218.

[18]Witten D M,Tibshirani R.A framework for feature selection in clustering[J].Journal of theAmerican StatisticalAssociation,2012,105(490):713-726.

[19]Hathaway R J,Bezdek J C.Fuzzy C-means clustering of incomplete data[J].IEEE Transactions on Systems,Man and Cybernetics:Part B Cybernetics,2001,31(5):735-744.

附中文参考文献：

[6]张孙力,杨惠中.基于改进的K近邻缺失数据补全[J].计算机应用与化学,2015,32(12):1499-1502.

[7]邹微,王会进.基于朴素贝叶斯的EM缺失数据填充算法[J].微型机与应用,2011,30(16):75-77.

[8]武森,冯小东,单志广.基于不完备数据聚类的缺失数据填补方法[J].计算机学报，2012,35(8):1726-1738.

[9]王凤梅,胡丽霞.一种基于近邻规则的缺失数据填补方法[J].计算机工程,2012,38(21):53-55.

[10]方匡南,谢邦昌.基于聚类关联规则的缺失数据处理研究[J].统计研究,2011,28(2):87-92.

[11]张赤,丰洪才,金凯,等.基于聚类分析的缺失数据最近邻填补算法[J].计算机应用与软件,2014,31(5):282-284.

[12]陈肇强,李佳俊,蒋川,等.基于上下文感知实体排序的缺失数据修复方法[J].计算机学报,2015,38(9):1755-1766.

[13]金连,王宏志,黄沈冰,等.基于Map-Reduce的大数据缺失值填充算法[J].计算机研究与发展,2013,50(S1):312-321.

[14]冷泳林,陈志奎,张清辰,等.不完整大数据的分布式聚类填充算法[J].计算机工程,2015,41(5):19-25.

[15]赵飞,刘奇志,张剡,等.一种大域数据流中缺失值的填充方法[J].南京大学学报:自然科学,2011,47(1):32-39.

[16]陈志奎,杨英达,张清辰,等.基于变量约简的物联网不完全数据填充算法[J].计算机工程与设计,2013,34(2):418-422.

[17]刘春英.基于变量依赖度的缺失值顺序填充算法[J].计算机应用与软件,2013,30(9):215-218.

Research on Block Imputation Algorithm for High Dimensional Correlation Missing Data*

YANG Jie1+,YANG Hu1,WANG Lubin1,JIN Xin1,GUO Hua2,YU Liangliang3
1.School of Information,Central University of Finance and Economics,Beijing 100081,China
2.Jingzhou Power Supply Company ICT Branch of State Grid Corporation,Jingzhou,Hubei 434000,China
3.Liaoning Power Supply Company ICT Branch of State Grid Corporation,Shenyang 110000,China

A

TP311

+Corresponding author:E-mail:yangjiecufe@163.com

YANG Jie,YANG Hu,WANG Lubin,et al.Research on block imputation algorithm for high dimensional correlation missing data.Journal of Frontiers of Computer Science and Technology,2017,11(10)：1557-1569.

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2017/11(10)-1557-13

10.3778/j.issn.1673-9418.1609010

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

*The Young Teachers Development Foundation of Central University of Finance and Economics under Grant No.QJJ1510(中央财经大学青年教师发展基金);the Technology Project of State Grid Corporation of China under Grant No.SGTYHT/14-JS-188(国家电网科技部项目).

Received 2016-09,Accepted 2016-11.

CNKI网络优先出版:2016-11-07,http://www.cnki.net/kcms/detail/11.5602.TP.20161107.1703.002.html

YANG Jie was born in 1992.He is an M.S.candidate at Central University of Finance and Economics.His research interest is data analysis.

杨杰（1992—），男，四川广元人，中央财经大学硕士研究生，主要研究领域为数据分析。

YANG Hu was born in 1983.He received the Ph.D.degree in statistics from Renmin University of China in 2014.Now he is a lecturer at Central University of Finance and Economics,and the member of CCF.His research interests include E-business,data analysis and computational statistics,etc.

杨虎（1983—），男，贵州贵阳人，2014年于中国人民大学统计学专业获得博士学位，现为中央财经大学信息学院讲师，CCF会员，主要研究领域为电子商务，数据分析与统计计算等。主持中央财经大学青年发展基金等项目。

WANG Lubin was born in 1960.He is a professor at Central University of Finance and Economics.His research interests include information management and financial informatization,etc.

王鲁滨（1960—），男，黑龙江哈尔滨人，中央财经大学继续教育学院院长、教授，主要研究领域为信息管理，金融信息化等。主持国家自然科学基金等项目。

JIN Xin was born in 1974.He received the Ph.D.degree in control theory and engineering from Donghua University in 2004.Now he is a professor at Central University of Finance and Economics,and the member of CCF.His research interests include big data analysis and business intelligence,etc.

金鑫（1974—），男，内蒙古乌海人，2004年于东华大学控制工程专业获得博士学位，现为中央财经大学信息学院教授，CCF会员，主要研究领域为大数据分析，商务智能等。

GUO Hua was born in 1972.He is an engineer at Jingzhou Power Supply Company ICT Branch of State Grid Corporation.His research interest is information system and management.

郭华（1972—），男，湖北荆州人，荆州供电公司信通分公司工程师，主要研究领域为信息系统运维及安全管理。

YU Liangliang was born in 1986.He is an engineer at Liaoning Power Supply Company ICT Branch of State Grid Corporation.His research interest is power system communication.

于亮亮（1986—），男，内蒙赤峰人，华北电力大学通信与信息系统专业硕士，国网辽宁省电力有限公司信息通信分公司工程师，主要研究领域为电力系统通信。