真实气体效应对MSL火星进入气动特性的影响研究
梁杰 李志辉 杜波强 方明
真实气体效应对MSL火星进入气动特性的影响研究
梁杰 李志辉 杜波强 方明
(中国空气动力研究与发展中心超高速所,绵阳 621000)
探测器超高速进入火星过程的高温真实气体效应对飞行稳定性和防热系统影响极大,需要在初步设计阶段对探测器的气动力热特性进行精确预测。文章构建了采用流场直角与表面非结构混合网格以及网格自适应的直接模拟蒙特卡洛方法,模拟稀薄环境高温真实气体效应的依赖于温度的多原子分子振动激发和8组份54化学反应模型。通过计算“火星探路者”外形气动力系数随攻角的变化,并与文献提供的计算结果对比,有较好的一致性,验证了该文算法的可靠性。文章模拟了“火星科学实验室”在火星大气环境70km高度、进入速度为5.85km/s下的高温真实气体效应对气动力、气动热和流场特征的影响。通过与完全气体计算结果对比,表明高温真实气体效应影响下的激波脱体距离减小,表面热流降低,轴向力系数增加、配平攻角减小、压心位置随攻角变化显著。
深空探测 火星进入 直接模拟蒙特卡洛方法 真实气体效应 气动特性
0 引言
在人类的深空探测活动中,火星是最热门的被探测行星。火星探测器的进入、减速和着陆(Entry,Descent and Landing,EDL)过程涉及穿越整个火星大气层,虽然历时很短,但由于探测器进入的速度很高,因此产生的气动力和气动热对探测器的飞行稳定性、着陆精度和热防护系统的影响极大,并经受严酷的气动加热和过载,是整个火星探测任务最危险、最重要的环节[1-3]。2011年11月,美国NASA成功发射了“火星科学实验室”(Mars Science Laboratory,MSL)探测器。MSL探测器采用升力式进入,与以往的火星探测任务相比,MSL探测器在质量和体积、防热罩直径、升阻比、降落伞直径、着陆点高度、着陆精度要求等参数设计方面都是最高的[4-5]。对MSL探测器进入火星大气的气动特性开展研究,对我国正在进行的火星探测任务应该具有较好的借鉴作用。
与返回地球的再入飞行不同,火星大气环境陌生且没有足够的基础数据作支撑,这对进入段探测器气动特性的精确预测带来很大的困难。与地球大气显著不同,火星大气主要由95.7%的CO2、2.7%的N2和1.6%的Ar组成,其大气压力和密度都比地球大气低约2个数量级,稀薄气体效应对探测器进入段气动特性的影响区域也更广。另外,火星大气温度比地球低,火星环境下的高超声速流动呈现雷诺数低、马赫数高的特点。探测器在高超声速绕流时将产生弓形激波,波后气体被加热并发生离解甚至可能电离,流动伴随复杂的化学反应。火星大气中CO2气体的分子振动特征温度低,高温气体的原子和分子能量通过碰撞在平动、转动、振动和电子模态之间相互转换,各个能量模态被激发,火星大气流动的高温真实气体效应相对更加明显。由于火星探测器的飞行数据稀缺,地面风洞实验难度也很大,因此计算模拟成为火星探测器进入段气动和防热问题研究的重要工具。国内开展火星大气高温真实气体影响研究采用的是求解连续流Navier-Stokes方程,化学反应模型采用的是5组份8反应[6]。而在进入段较广的区域内稀薄气体效应与高温真实气体效应耦合存在,需要采用模拟稀薄气体流动的直接模拟蒙特卡洛方法(Direct Simulation Monte Carlo,DSMC)以及更加精细的化学反应模型[7]。
为了建立火星大气环境下能够模拟复杂流动现象和气动力热特性的数值研究工具,深刻了解高温真实气体效应对火星探测器进入段稀薄过渡流区气动力、气动热以及流场特征的影响规律,本文在模拟探月返回器地球大气环境热化学非平衡流动DSMC方法[8]的基础上,构建了模拟火星大气环境下8组份54化学反应的热化学非平衡流动DSMC方法。在对本文数值算法进行对比验证的基础上,计算分析了完全气体模型和真实气体模型、进入速度5.85km/s和高度70km条件下MSL外形的气动特性和流场特征。
1 DSMC方法
1.1 计算网格及网格自适应
在DSMC方法中,流场中的网格是用来选取可能的碰撞分子对以及对宏观流动参数取样。流场采用均匀的直角坐标网格,追踪分子的效率非常高,计算区域内的模拟分子可以直接根据分子的位置坐标来确定分子所属的网格,而不必跟踪分子从一个网格运动到另一个网格,其缺点是无法精确地描述物面边界。本文结合直角网格计算的高效率以及表面非结构网格对飞行器几何外形的精细描述,建立了混合网格结构的DSMC数值模拟方法。在描述物面几何形状的非结构网格建立以后,直接将其嵌入到直角网格的流场中,使DSMC计算对流场网格的依赖程度大大降低。通过联合求解分子运动轨迹方程和物面三角形面元上任一点的位置方程,可以唯一确定出分子与物面的碰撞点坐标,从而解决了这种混合网格流场分子运动与物面碰撞的难题[9]。另外,对分子在物体三角形面元上碰撞、反射前后的流场参数进行统计取样就可以获得飞行器的整体气动力特性、表面力以及热载荷分布。
为了解决流场中因激波压缩以及气体膨胀后引起的密度急剧变化的流动特征,计算中采用了网格自适应的策略。即在背景网格的基础上,根据流场中密度梯度的变化分别对碰撞网格和取样网格进行细 化[10]。由于流场的梯度沿各个方向的变化是不同的,梯度变化大的方向网格细分的更密一些,因此沿三个坐标方向是各自独立地进行自适应,碰撞分子则是在自适应后最小的亚网格内选取,从而保证了计算的空间精度。
1.2 分子振动激发的模拟
CO2为直线型三原子分子,常温条件下具有3个平动自由度和2个转动自由度,在高温条件下振动会被部分或完全激发。根据分子光谱测定实验[11],高温CO2分子具有3个振动模态,分别为弯曲模态(特征温度为960K)、对称拉伸模态(特征温度为1 919K)和反对称拉伸模态(特征温度为3 382K)。文献[12]证实了CO2的3个振动模式具有相同的松弛速率,因为弯曲模态的振动特征温度最低,而大部分的振动能量都以这种模态存在,因此本文在计算中仅考虑弯曲模态的振动特征温度。
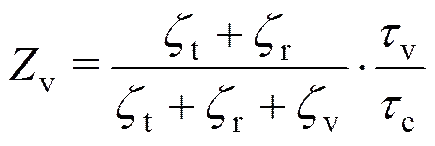
(2)
式中和分别是当地的气体压力和温度;是拟合参数。Millikan和White在高温激波管内通过干涉仪观测了气体分子振动松驰过程[13],在1×104K的温度范围内,给出了拟合参数:
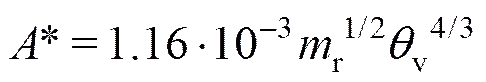
式中r是碰撞分子的折合质量;v是振动特征温度。
随着温度升高,式(2)将偏离实验结果。Park[14]给出了高温修正的为
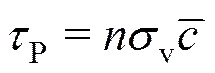
式中是数密度(m–3);是分子振动碰撞截面(=1×10–20m2);是分子平均热速度。
1.3 化学反应模拟
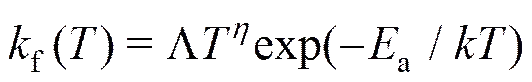
式中a是反应中需要的活化能;和是常数,由实验定出;是Boltzmann常数。
根据上式可推导出化学反应几率r的表达式为[15]:
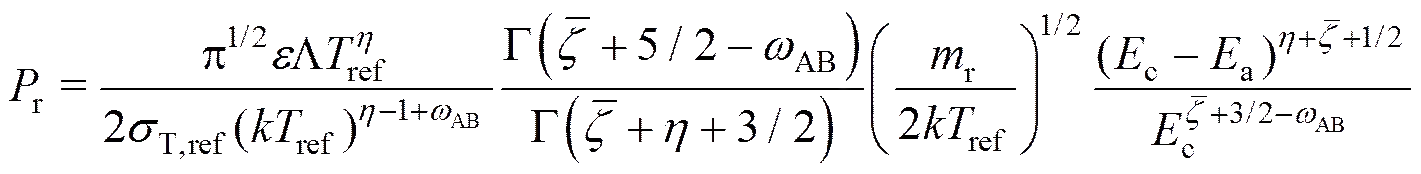
火星大气的化学反应模型取为8组份54反应[16],包括 40个离解反和14个置换反应:
1)40个离解反应
CO+M → C+O+M M= C,CO,CO2,N,N2,NO,O,O2
CO2+M → CO+O+M M= C,CO,CO2,N,N2,NO,O,O2
N2+M → N+N+M M= C,CO,CO2,N,N2,NO,O,O2
NO+M → N+O+M M= C,CO,CO2,N,N2,NO,O,O2
O2+M → O+O+M M= C,CO,CO2,N,N2,NO,O,O2
2)14个置换反应
CO+CO → CO2+C N+CO → NO+C
NO+CO → CO2+N O+CO → O2+C
O2+CO → CO2+O C+CO2→ CO+CO
N+CO2→ NO+CO O+CO2→ O2+CO
O+N2→ NO+N C+NO → CO+N
N+NO → N2+O O+NO → O2+N
N+O2→ NO+O C+O2→ CO+O
2 计算结果分析
2.1 算法验证
为了考核本文构建的DSMC方法对火星探测器气动力特性的模拟精度,对美国“火星探路者”(Mars Pathfiner)外形的气动力系数进行了计算,并与文献[17]中采用国际知名DSMC模拟软件DAC计算的结果进行了对比。选取了两个克努森数()下的来流条件进行计算,攻角范围0°~30°,来流温度150K,气体组份为95.37%的CO2和4.63%的N2,其它初始条件与文献[17]中的一致,详见表1,表中的Kn,HS表示采用硬球(Hard Sphere,HS)分子模型计算的来流克努森数。由于来流的气体密度较低,计算中仅考虑气体分子的转动和振动激发,不考虑化学反应。
表1 计算“探路者”外形的的来流条件

Tab.1 Conditions for Mars Pathfinder calculations
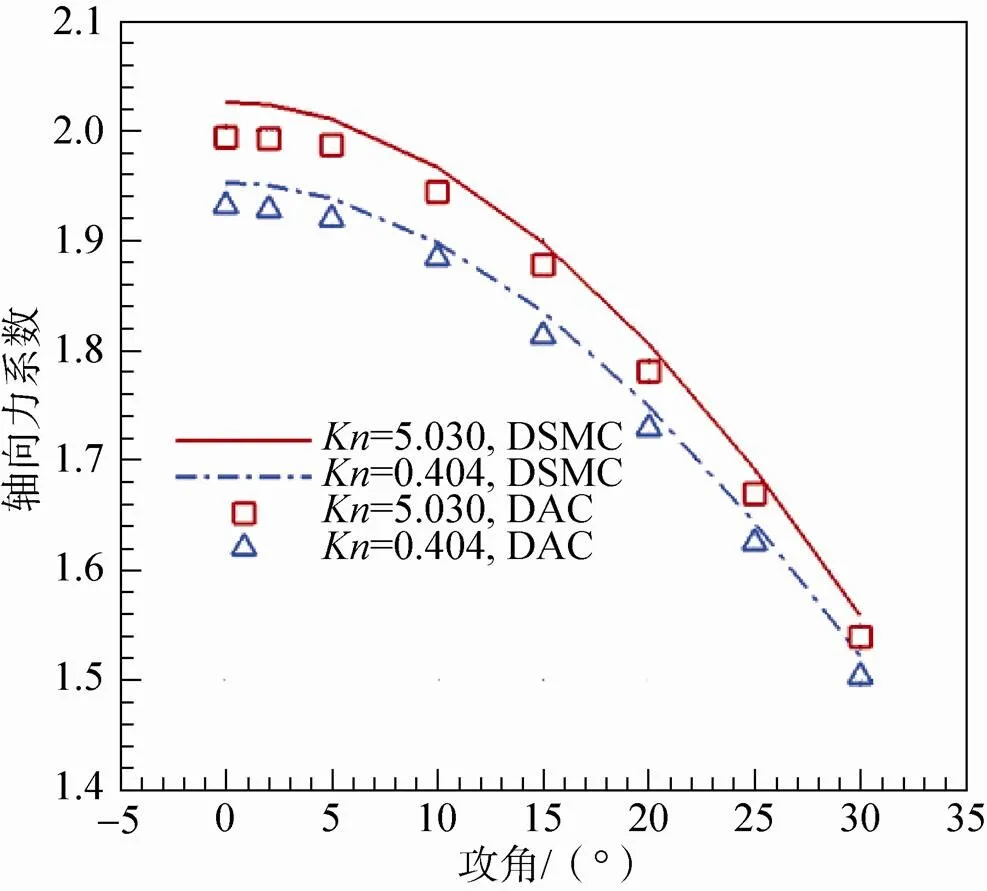
图1分别给出了计算的“火星探路者”轴向力系数、法向力系数和对头部顶点的俯仰力矩系数的对比情况,本文计算值均在数值上略大于文献值,这种差别可能与两种算法采用的流场网格数量和模拟分子的总数不同有关。轴向力系数随着攻角增大两者的偏差不断减小,最大相对偏差小于2%。法向力系数则是随攻角增加偏差增大,最大相对偏差小于10%。俯仰力矩系数两者的一致性较好。上述气动力系数随攻角变化的一致性较好地验证了本文构建的DSMC数值算法的可靠性,可以用于火星探测器稀薄气动特性的研究。
(a)轴向力系数 (b)法向力系数
(a)Axial force coefficient (b)Normal force coefficient
(c)俯仰力矩系数
2.2 真实气体效应对MSL气动特性影响分析
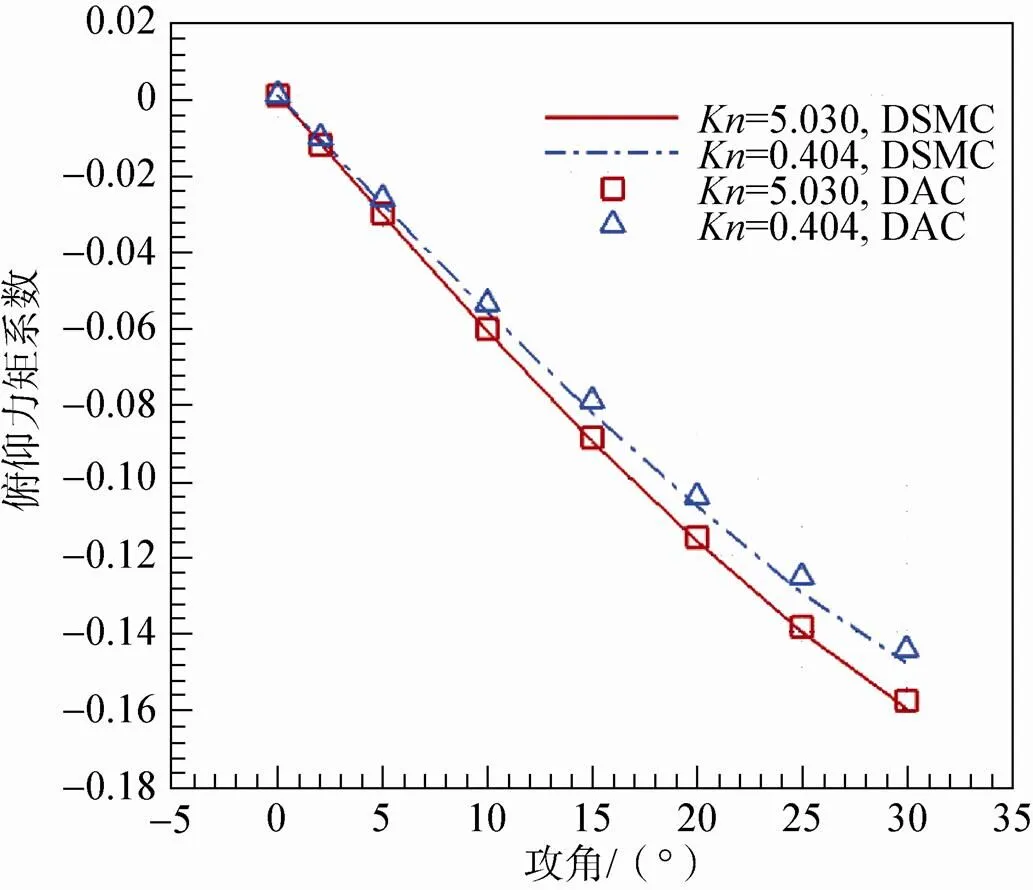
以MSL探测器火星进入的速度来说,在70km高度是稀薄气体效应与高温真实气体效应耦合作用比较严重的区域,无论是连续流的CFD方法还是基于分子碰撞理论的DSMC方法精确模拟都非常困难。由于该高度的气体分子平均自由程较小,DSMC方法的计算量非常大,为了保证本文的计算精度,将流场的初始背景网格设置为1.62×107,自适应后的碰撞网格超过9×107,总的模拟粒子数最高达到了6×108,并采用了大规模并行计算。MSL外形和尺寸详见文献[18],来流初始参数分别取为密度7.639×10–6kg/m3(70km高度)、温度150K、气体组份为95.37%的CO2和4.63%的N2,探测器进入速度5 845.4m/s,攻角–25°~0°。壁面温度设置为500K、完全漫反射,仅计算对称的半个流场。计算中考虑两种气体模型:完全气体模型,仅考虑了分子的转动激发;真实气体模型,考虑分子的转动、振动能量激发以及8组份54化学反应。
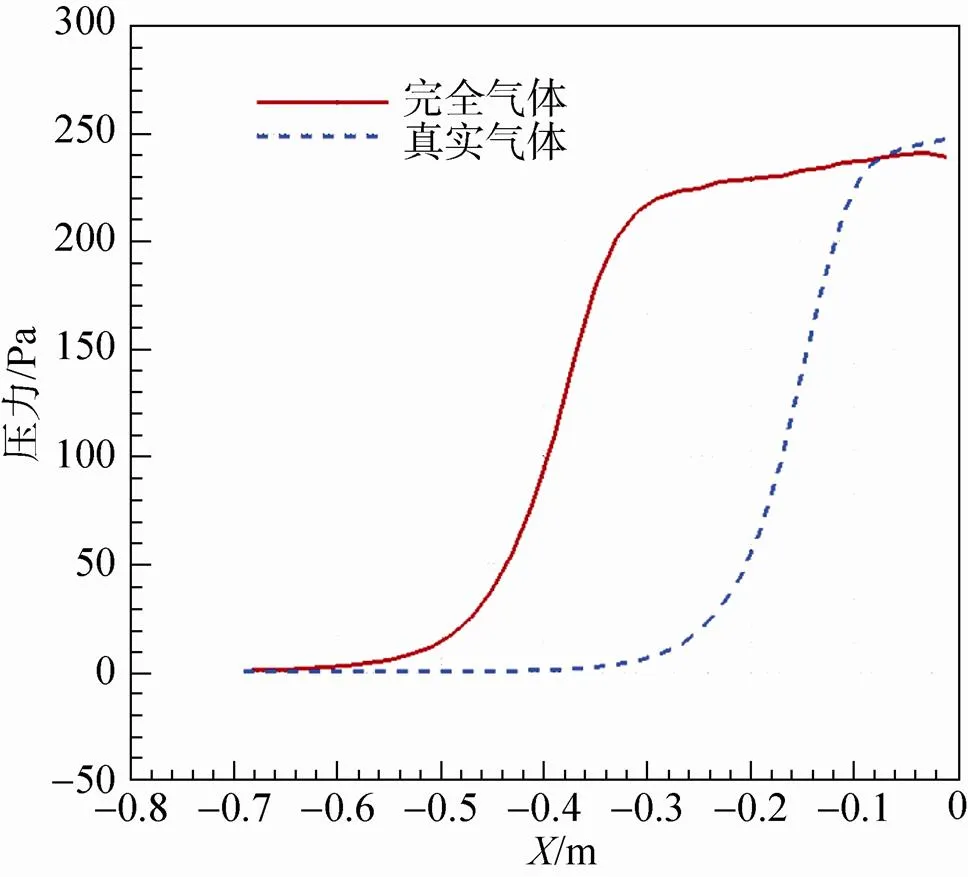
图2给出了0°攻角时采用两种气体模型计算的流场压力和温度等值线分布的对比。图形的上半部分为完全气体模型结果,下半部分为真实气体模型结果。可以看出,在高温气体热化学非平衡效应的影响下,激波形状发生了明显的变化,头部弓形激波更加贴体,驻点温度明显降低,波后温度分布明显不同,在飞行器后体的尾迹流动中出现大范围的低温区。靠近壁面的高压力区域要大于完全气体结果。主要原因是高温真实气体影响下的激波层变薄,并且靠近物面,波后气体的压缩较强所致。另外,波后气体分子之间的碰撞,引起分子振动激发和化学反应,消耗了大量的分子碰撞能量,使流场的温度有较大程度的下降。
(a)压力 (b)温度
图3给出了沿对称轴的压力和温度分布,虽然真实气体模型的驻点压力略高于完全气体模型,但结合图2可知高压力的分布范围大,会引起轴向力系数的增加。而驻点温度降低了近一半,也会造成表面热流的急剧下降,如图4所示热流系数在肩部区域降低了近一半。因此,计算中采用考虑分子振动激发以及化学反应的真实气体模型,可以更加准确地预测流动中复杂的物理现象和气动力热特性。
(a)压力 (b)温度
图5是0°攻角时真实气体模型计算的化学组份摩尔分数沿对称轴线的变化,图中显示出较强的化学非平衡流动特征。经过激波的压缩,在波后的激波层区域流场温度升高,压缩后的气体分子之间碰撞频率增加,导致化学反应增强,CO2发生较大程度的离解,浓度下降,生成的CO和O的浓度依次升高,成为仅次于CO2的组份。发生置换反应生成的O2的浓度相对较低,最高仅达到与N2初始浓度相同的含量。化学反应生成的其它组份NO、C和N的含量更低。图6展示了含量较高的CO2、CO、O和O2等4个组份的对称面流场摩尔分数分布情况。在肩部后方及尾流区,CO2的浓度都比较低,CO在肩部后的尾流中浓度最大,O的浓度在肩部以后的壁面附近浓度稍高一些,而O2的浓度较低散布较大。
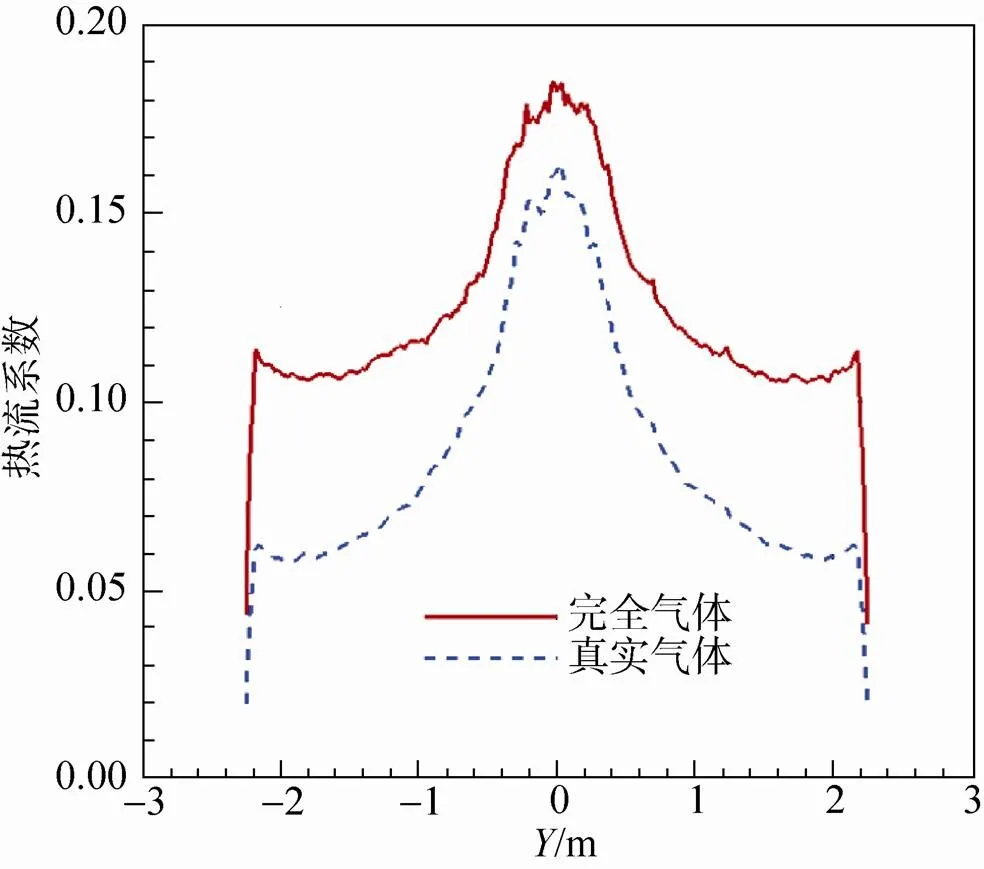
图4 沿对称锥面热流系数分布
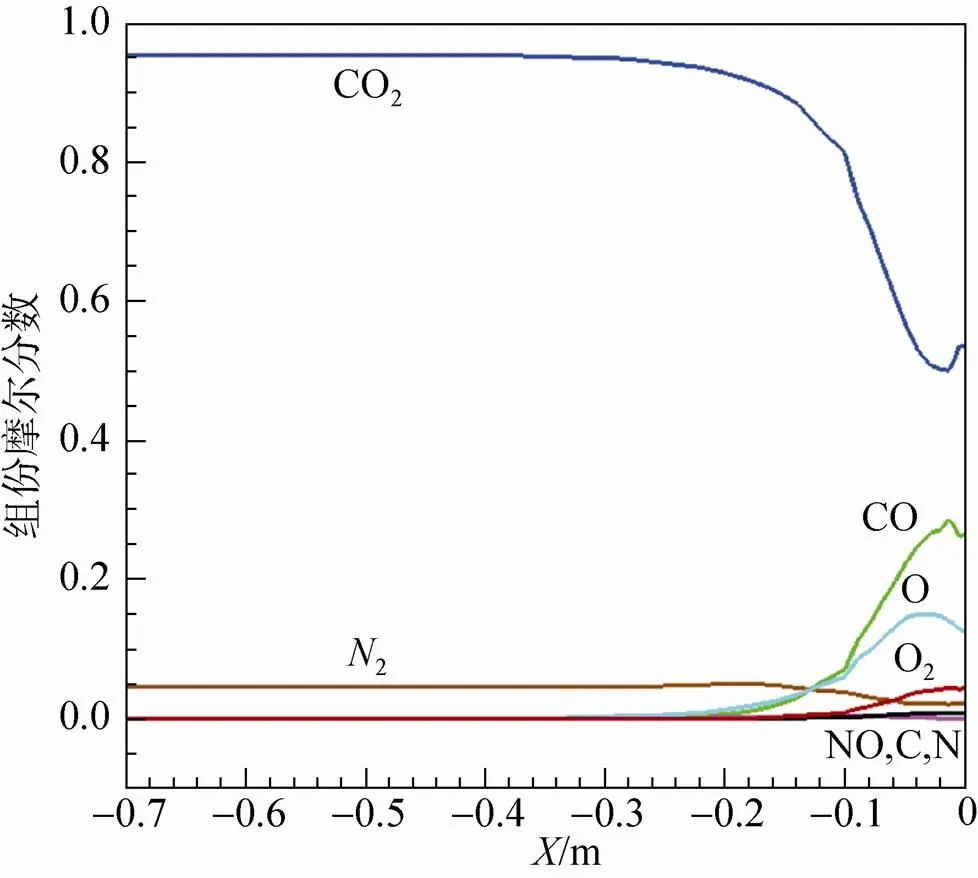
图5 化学组份摩尔分数沿对称轴线分布
图7给出了两种模型计算的气动力系数随攻角的变化曲线。轴向力系数随着攻角绝对值的增大两者的偏差逐渐减小,在0°攻角时的相对偏差最大达到5.6%,法向力系数两者相差很小,高温真实气体效应对质心的俯仰力矩系数和压心系数的影响较大,配平攻角减小1.2°,压心位置随攻角发生较大范围的变化。从前面的流场结果可以知道,对于这种头部70°钝锥外形,气动力主要作用在70°钝锥的表面上。高温真实气体效应影响下的锥面压力在气体压缩区域高(迎风面)、膨胀区域低(背风面),由于0°攻角整个锥面都处在迎风面,造成0°攻角的轴向力系数与完全气体的偏差最大。而在大攻角情况下,整个70°钝锥的锥面上迎风面压力高、背风面压力低,两者对轴向力系数的贡献互相抵消,因此数值上超过15°攻角以后,真实气体与完全气体计算的轴向力系数偏差较小。由于气动力系数主要由作用在锥面上的压力贡献,因此这种钝体外形的法向力系数较小,气体模型对法向力系数的影响也比较小。也正是在锥面上压力分布不同气体模型存在着较大的差异,引起俯仰力矩系数和纵向压心系数的较大不同。完全气体下的纵向压心系数随攻角变化不大,但真实气体效应影响下的纵向压心系数最大有近58%的变化量。–5°攻角的压心位置最靠前,随着攻角绝对值的增大压心位置迅速后移,在–15°攻角以后逐渐超过了完全 气体。
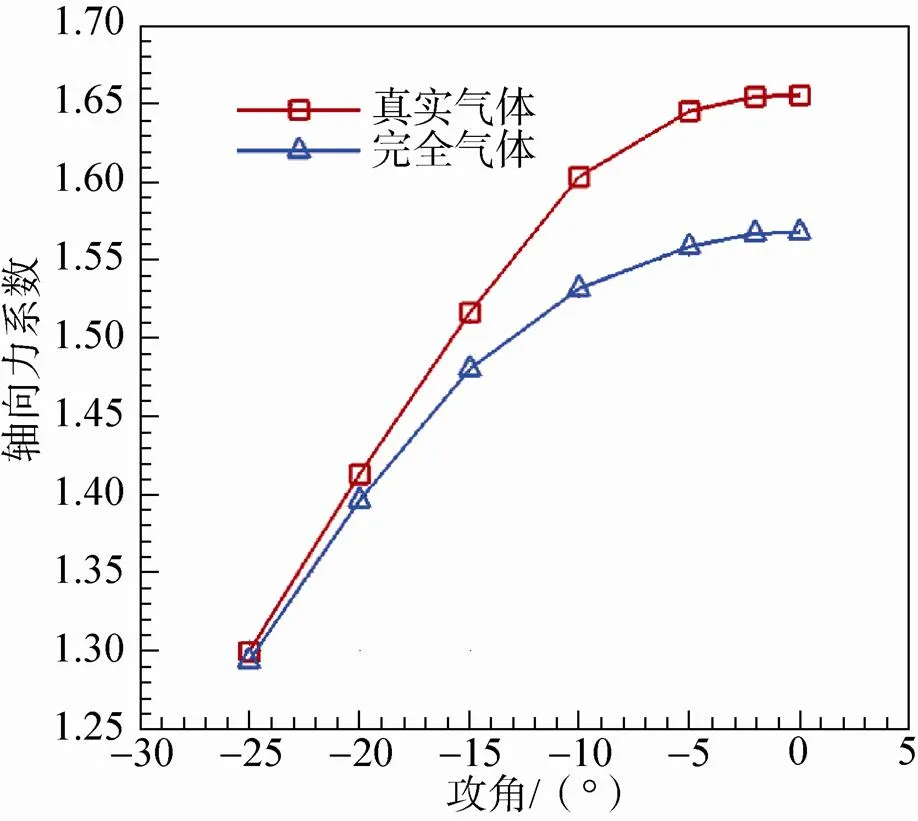
(a)轴向力系数 (b)法向力系数
(a)Axial force coefficient (b)Normal force coefficient
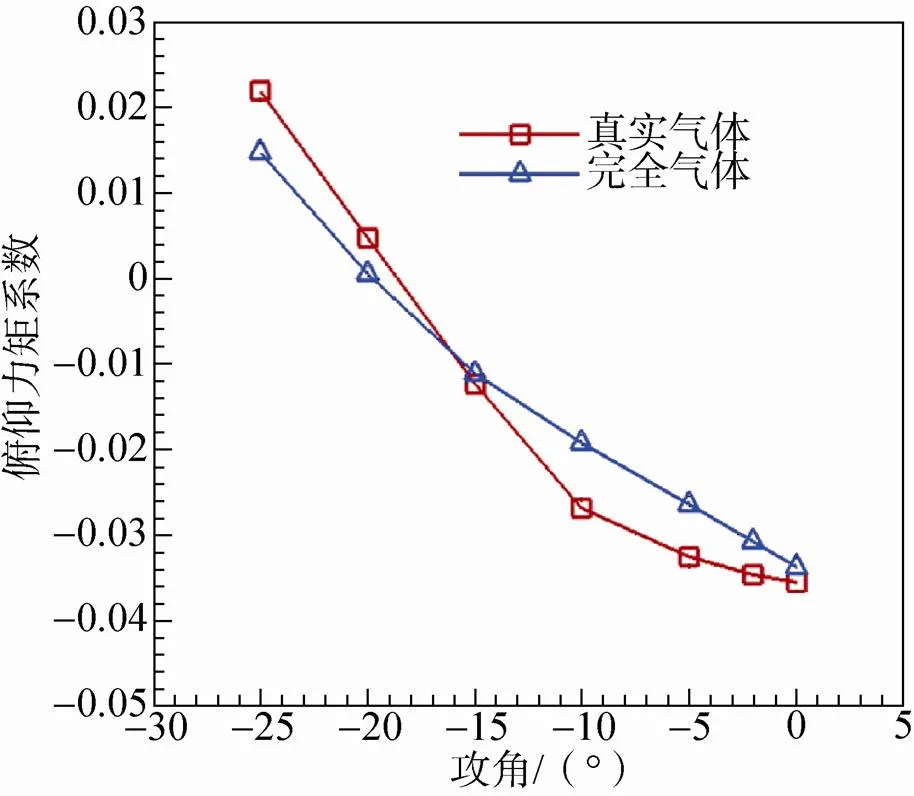
(c)俯仰力矩系数 (d)压心系数
3 结束语
本文提供了模拟探测器超高速进入火星大气环境高温真实气体效应的DSMC方法,采用流场直角与表面非结构混合网格及网格自适应,构建了多原子分子的振动激发及8组份54化学反应模型,可以作为火星探测器进入段稀薄气动力/气动热的有效预测分析工具。通过与文献中提供的“火星探路者”外形气动力系数的对比,验证了本文算法的可靠性,研究了“火星科学实验室”外形在70km高度的气动力热和流场特性,并与完全气体模型结果进行了对比分析,可以得到以下几点结论:
1)高温真实气体效应导致探测器头部激波脱体距离显著减小,波后压力上升,温度急剧下降。
2)经过激波的压缩,CO2气体大量离解,在探测器后体及尾迹流场中生成大量的CO、O以及少量的O2,其它化学组份的含量较微弱;化学反应消耗了流动中的大量能量,引起表面热流的较大降低。
3)随攻角绝对值增大,考虑分子振动和化学非平衡的真实气体和完全气体的法向力系数基本一致,轴向力系数相差很大并且随着攻角增大偏差减小。
4)攻角较大时真实气体效应影响的俯仰力矩系数高于完全气体,小攻角时正好相反,使此时的配平攻角相比完全气体减小1.2°。
5)高温真实气体效应对纵向压心位置影响显著,小攻角下的压心位置比完全气体模型明显前移,随着攻角增大迅速后移,在计算攻角范围内压心系数有近58%的变化量,而完全气体的压心系数随攻角变化不大。
[1] BRAUN R D, MANNING R M. Mars Exploration Entry, Descent and Landing Challenges [J]. Journal of Spacecraft and Rockets, 2007, 44(2): 310-323.
[2] GAZARIK M J, WRIGHTM J, LITTLE A, et al. Overview of the MEDLI Project: Aerospace Conference, 2008 IEEE[C]. Big Sky, MT: IEEE, 2008. DOI:10.1109/AERO.2008.4526285.
[3] 贾贺, 荣伟. 火星探测器减速着陆技术分析[J]. 航天返回与遥感, 2010, 31(3): 6-14.JIA He, RONG Wei. Mars Exploration Deceleration Landing Technology Analysis[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(3): 6-14. (in Chinese)
[4] SCHOENENBERGER M, DYAKONOV A, BUNINGP, et al. Aerodynamic Challenges for the Mars Science Laboratory Entry, Descent and Landing: Fluid Dynamics and Co-located Conferences[C]// 41st AIAA Thermophysics Conference, San Antonio, TX, 2009.
[5] 鲁媛媛, 荣伟, 吴世通. “火星科学实验室”EDL方案及其新技术分析[J]. 航天器工程, 2012, 21(5): 117-123. LU Yuanyuan, RONG Wei, WU Shitong. Introduction and New Technology of EDL System of MSL[J]. Spacecraft Engineering, 2012, 21(5): 117-123. (in Chinese)
[6] 吕俊明, 程晓丽, 王强. 火星科学实验室气动特性数值分析[J]. 力学与实践, 2013, 35(1): 31-35. LYU Junming, CHENG Xiaoli, WANG Qiang. Numerical Aerodynamic Analysis of Mars Science Laboratory[J]. Mechanics in Engineering, 2013, 35(1): 31-35. (in Chinese)
[7] 王保国, 李耀华, 钱耕. 四种飞行器绕流的三维DSMC计算与传热分析[J]. 航空动力学报, 2011, 26(1): 1-20. WANG Baoguo, LI Yaohua, QIAN Gemg. Three-dimensional DSMC Calculation and Heat Transfer Analysis of Four Capsules for Hypersonic Rarefied Conditions[J]. Journal of Aerospace Power, 2011, 26(1): 1-20. (in Chinese)
[8] 梁杰, 李志辉, 杜波强, 等. 探月返回器稀薄气体热化学非平衡特性数值模拟[J]. 载人航天, 2015, 21(3): 295-302. LIANG Jie, LI Zhihui, DU Boqiang, et al. Numerical Simulation of Rarefied Gas Thermochemical Nonequilibrium when Lunar Exploration Vehicle Re-entering into Atmosphere[J]. Manned Spaceflight, 2015, 21(3): 295-302. (in Chinese)
[9] 梁杰, 阎超, 杜波强. 基于两级直角网格结构的三维DSMC算法研究[J]. 空气动力学学报, 2010, 28(4): 466-471. LIANG Jie, YAN Chao, DU Boqiang. An Algorithm Study of Three-dimensional DSMC Simulation based on Two-level Cartesian Coordinates Grid Structure[J]. ActaAerodynamica Sinica, 2010, 28(4): 466-471. (in Chinese)
[10] 梁杰, 阎超, 杨彦广, 等. 过渡区侧向喷流干扰的并行DSMC数值模拟研究[J]. 宇航学报, 2011, 32(5): 1012-1018. LIANG Jie, YAN Chao, YANG Yanguang, et al. Parallel DSMC Simulation of Lateral Jet Interaction in Rarefied Transitional Region[J]. Journal of Astronautics, 2011, 32(5): 1012-1018. (in Chinese)
[11] MCBRIDE B J, HEIMIL S, EHLERS J G, et al. Thermodynamic Properties to 6000K for 210 Substances Involving the First 18 Elements [R]. NASA-SP-3001, 1963.
[12] CAMAC M. CO2Relaxation Processes in Shock Waves[C]// Fundamental Phenomena in Hypersonic Flow. Ithaca NY: CornellUniv. Press, 1966: 195-215.
[13] MILLIKAN R C, WHITE D R. Systematics of Vibrational Relaxation[J]. Journal of Chemical Physics, 1963, 39(12): 3209-3213.
[14] PARK C. Problems of Rate Chemistry in the Flight Regimes of Aeroassisted Orbital Transfer Vehicles: Progress in Astronautics and Aeronautics[C]//19th Thermophysics,Snowmass, United States,AIAA Paper 84-1730, 1984. DOI: 10.2514/5.9781600865718.0511.0537.
[15] BIRD G A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows[M]. Oxford: Clarendon Press, 1994.
[16] HASHD B, HASSAN H A. Monte Carlo Simulation of Entry in the Martian Atmosphere[J]. Journal of Thermophysics and Heat Transfer, 2015, 7(2): 228-232.
[17] MOSS J N, BLANCHARD R C, WILMOTH R G, et al. Mars Pathfinder Rarefied Aerodynamics: Computations and Measurements[J]. Journal of Spacecraft and Rockets, 2015, 36(3): 330-339.
[18] SCHOENENBERGER M, NORMAN J V, KARLGAARD C, et al. Assessment of the Reconstructed Aerodynamics of the Mars Science Laboratory Entry Vehicle[J]. Journal of Spacecraft and Rockets, 2014, 51(4): 1076-1093.
(编辑:陈艳霞)
Numerical Research of Real Gas Effect on MSL Mars Entry Aerodynamic Characteristics
LIANG Jie LI Zhihui DU Boqiang FANG Ming
(Hypervelocity Aerodynamics Institute, China Aerodynamics Research & Development Center, Mianyang 621000, China)
The high temperature real gas effects have great impact on flight stability and thermal protection system during Mars exploration vehicles entry in the Martian atmosphere at hypersonic speed. The precise prediction on aerothermodynamic characteristics should be performed in preliminary design stage. The direct simulation Monte Carlo (DSMC) method is established on a hybrid structure of Cartesian coordinate mesh, surface unstructured triangular cell and adaptive grid procedure. Temperature dependence of polyatomic molecules vibrational excitement and eight species and fifty-four chemical reaction model are included to simulate real gas effects in rarefied environment. The computed Mars Pathfinder aerodynamic coefficient variations with angles of attack have good agreements with reference results to verify the reliability of present algorithm. The Mars Science Laboratory (MSL) aerothermodynamics are simulated in entry speed of 5.85 km/s at 70km altitude. The effects of high temperature real gas on aero-force, aero-thermal and flowfields are investigated. Compared with perfect gas model, the results show that real gas effects reduce the standoff distance of shock wave and surface heat flux, make axial coefficients increase, trim angle decrease and pressure center position vary significantly with angle of attack.
deep space exploration; Martian entry; direct simulation Monte Carlo method; real gas effect; aerodynamics
V211.3
A
1009-8518(2017)04-0008-10
10.3969/j.issn.1009-8518.2017.04.002
梁杰,男,1966年生,2014年年获北航流体力学专业博士学位,现任中国空气动力研究与发展中心超高速所研究员。研究方向为稀薄气体动力学的数值方法及应用研究。E-mail:liangjie29501@163.com。
2016-12-05
973 计划(2014CB744100);国家自然科学基金(91530319、11325212)

