不同攻角下超声速降落伞伞绳的影响研究
薛晓鹏 温志湧 汪运鹏 张德良
不同攻角下超声速降落伞伞绳的影响研究
薛晓鹏1温志湧2汪运鹏3张德良3
(1 中南大学航空航天学院,长沙410083)(2 香港理工大学深圳研究院,深圳 518057)(3 中国科学院力学所高温气体动力学国家重点实验室,北京 100190)
文章基于一种简易“浸入边界技术”与流固耦合方法对超声速来流条件下的三维降落伞系统进行了数值模拟。研究中,降落伞系统包括前体和伞体,两者通过伞绳连接。文章的研究目的是分析不同攻角下降落伞伞绳对于降落伞系统周围复杂非定常流场的影响,以及对降落伞性能表现的影响。结果表明:在较小的前体和伞体距离下,由于攻角的影响,非定常流场结构呈现上下不对称,并且上下伞绳激波形成时间不同步。随着攻角的增加,上下面的伞绳激波形成时间出现推迟,并且有变弱的趋势。另外,由于攻角与伞绳的综合影响,伞内表面的时间平均压力分布在5º攻角时最小,而在10º攻角时最大,阻力系数却随着攻角的增加而增加。
超声速降落伞 伞绳 攻角 数值模拟 着陆
0 引言
在NASA的“火星科学实验室”(Mars Science Laboratory,MSL)探测任务中,“好奇号”探测器已经成功地着陆在火星表面。“好奇号”在进入火星大气层以后从超声速到亚声速的减速过程是借助于超声速降落伞而完成[1]。近几十年来,超声速降落伞的研究工作吸引了全世界的研究学者,其中降落伞伞绳对于降落伞系统性能表现的影响研究也是备受关注。在20世纪60年代,NASA就已经开展了针对降落伞伞绳对于超声速降落伞性能影响的风洞试验研究,文献[2]发现伞绳长度比(伞绳长度与伞体直径之比)直接影响降落伞系统的阻力性能,且受来流速度的显著影响。文献[3-4]观测到了伞绳对于超声速降落伞的伞前激波具有一定的影响。文献[5]进一步检查了伞绳等对于单伞和群伞的飞行特性影响。近年来,美国NASA及其合作小组对缩比MSL降落伞模型进行了超声速条件下试验和数值的充分调查[6-8],发现降落伞伞绳激波在伞绳附近形成,并影响了超声速流的不稳定性进而影响柔性伞衣的呼吸振动。随着计算机技术的发展,降落伞问题的数值模拟已经取得了显著的进步。然而,伞绳在数值模拟中一直作为边界条件,起到系统受力平衡的作用[9-14],对于超声速降落伞周围复杂流场影响的数值模拟研究却鲜有报道。文献[15]应用了一种简易“浸入边界技术”(Immersed Boundary Technique)首次模拟了伞绳在非定常流场中形成的激波过程以及研究了其对于超声速降落伞非定常流场的影响,该结果与日本航空航天局(JAXA)的试验结果非常吻合,并与美国NASA的喷气推进实验室的超声速降落伞试验结果相一致。
本研究将应用浸入边界技术进一步对三维超声速降落伞进行数值模拟,分析不同攻角下降落伞伞绳对于系统周围复杂流场结构的影响以及对降落伞性能表现的影响。
1 三维降落伞模型
本研究中以三维降落伞系统为研究对象,其简化模型包括太空舱(前体)和降落伞伞衣,如图1所示。伞体和前体之间用伞绳与连接轴连接。伞体是一个直径为的半球简化刚体模型,前体是一个呈锥形的简化模型,半锥角为20º,前表面的直径是,是从前体前表面到伞体入口的直线距离,是攻角,是伞体的厚度。超声速降落伞的两个关键设计参数分别为拖拽距离系数()和前体—伞体的直径比()。本研究中,前体与伞体入口的距离=57mm,通过伞绳连接。伞绳数为8,相邻伞绳间隔角度为45º,截面直径1.2mm,绳长为66mm。以上降落伞设计参数与日本航空航天局(JAXA)试验模型保持一致,更多细节参考文献[15]。其研究目的是与文献[15]中的降落伞系统(=57mm,=24mm)相比较来检验伞绳在不同攻角下对于降落伞周围复杂流场结构及阻力性能的影响机理。本研究中的拖拽距离系数等参数如表1所示,其中拖拽距离系数小于NASA的MSL降落伞模型试验中的名义值(大约10)[9],这是因为本降落伞系统周围的流场模型更为复杂[16-19],而通过伞绳对流场模型影响的机理研究可以更深入地理解降落伞系统周围的流场模型及其影响因素。
2 计算条件和数值方法
2.1 计算条件和计算网格
本研究计算中来流条件如表2所示,来自文献[15,19]中的试验条件。由于降落伞系统的轴对称特性,计算网格由子午线断面旋转而成,其三维视图参考文献[15],网格单元数约5×106。网格依赖性检验可参考文献[15]。

图1 三维降落伞模型
表1 降落伞系统外形参数

Tab.1 Specifications for the different parachute systems
表2 本研究计算所用的来流条件

Tab.2 Free stream conditions employed in this study
2.2 数值方法
(1)流场计算
本研究采用三维可压缩Navier–Stokes方程,数值求解三维降落伞系统周围的超声速流场,控制方程采用有限体积法进行离散。在本计算程序中,无粘通量选择SHUS格式(Simple High-resolution Upwind Scheme)[21],并采用Van Albada限制器通过三阶MUSCL方法进行差值以提高精度。粘性通量采用二阶中心格式离散,时间推进则采用三阶TVD Runge–Kutta格式进行。边界条件的处理上,降落伞表面采用无滑移,等壁温。入口边界赋来流参数,出口边界采用外插处理。
(2)结构计算
在本研究中,降落伞模型中伞绳的结构计算选用了质量–弹簧–阻尼(Mass-Spring-Damping,MSD)模型[13,15, 22-23]来模拟伞绳的结构动力学,控制方程是基于作用在每一个控制点的牛顿第二定律。在本研究中,文献[15]中伞绳结构的假设,设定伞绳为刚性,伞绳的非定常运动与流场结构的耦合过程将在下一步的研究中予以考虑。
(3)流固耦合格式
流固耦合方法[13, 15, 23]如图2所示,伞绳表面上的压力分布作为流体力,被应用到每一个伞绳控制点的计算中。然后这些计算结果再通过“浸入边界技术”[13, 15, 23]被传送到流场计算中。
为了同时计算流体和结构,弱耦合方法[13, 15, 23](图3所示)被应用到该计算中。在计算的每一个时间步(),从结构计算(=0时,伞结构的初始模型)中得到的控制点信息被传递到该计算步()的流场计算中,而弱耦合方法又使得流场计算中获得的流场力被用于下一个时间步(+1)的结构计算中,然后随着时间步的增加而进行循环迭代。
文献[15]已应用以上数值方法(流体计算、结构计算、流固耦合方法)对三维降落伞系统的伞绳影响进行了数值模拟,观测到了伞绳激波的形成,分析了其对降落伞系统周围流场模型的影响机理,得到了与试验结果相吻合的结果。该研究方法被拓展到本研究中进一步研究不同攻角下伞绳的影响机理。
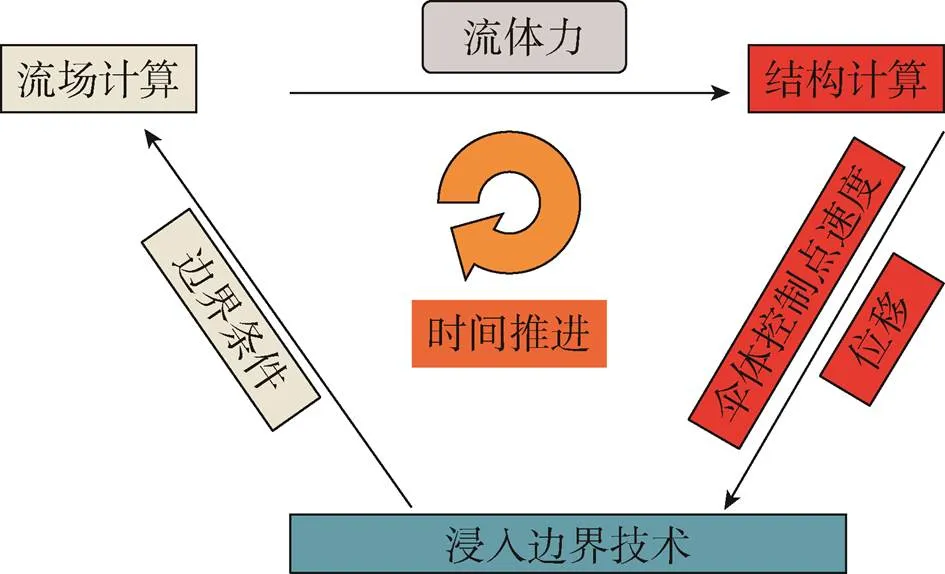
图2 流固耦合方法
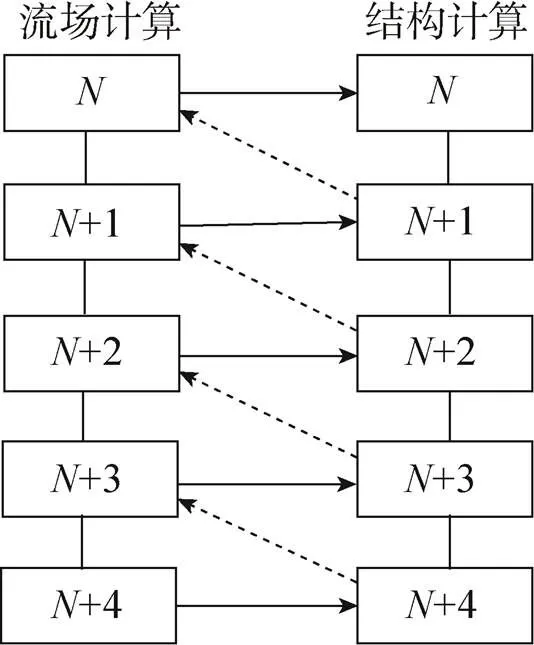
图3 弱耦合格式
3 计算结果与分析
3.1 非定常流场结构的影响
在文献[15]中考察了攻角=0°时伞绳影响下的降落伞系统非定常流场结构,流场模式仍然为“脉动流场模型”[16-19],然而,伞绳激波的形成对伞前激波与前体尾流的相互作用存在一定影响,显著地增加了降落伞系统周围流场的不稳定性。当=5°时,选取降落伞系统一个脉动周期内的瞬时流场如图4所示。需要注意的是,因为本研究主要着重于受伞绳影响的流场结构,所以图4中上下面均包含伞绳。图中,为时间、5为脉动流场的周期、46为非定常流场变化的一个周期帧数。含伞绳与未受伞绳结构影响的流场结构已经在文献[15]中做了对比分析,此文不再赘述。从图4中可以发现由于攻角的影响,非定常流场结构呈现上下不对称,并且上下伞绳激波形成时间不同步(图4(a))。另外可以发现,上面的伞绳激波有一个由弱增强的过程,当伞内高压而形成的伞前激波与伞绳激波相交(图4(d)),伞绳激波开始脱离伞绳,向上游传播,同时与前体尾流的相互作用变得剧烈;相比之下,下面的伞绳激波处于稳定状态,其也与伞前激波出现相互作用,但由于攻角的影响,伞内压力分布不均匀,下面的伞前激波较弱,使得上下的流场结构出现不对称。在伞内高压的推动下,伞前激波(与伞绳激波相重合)向上流传播,并与前体激波相交并相互作用(图4(f)–(h)),使得降落伞系统周围压力升高,进而推动前体激波/伞前激波相互作用区域向侧向扩展(图4(h));当系统周围压力减弱,前体激波/伞前激波相互作用区域顺流而下(图4(i)),并且两者相互作用亦愈来愈弱,直至消失,并进入下一个周期。
当攻角为=10°时,基本的流场特征变化规律与驱动机理与=5°时相类似,但是亦有不同表现,见图5。图中10为脉动流场的周期。可以发现,随着攻角的增加,上下面的伞绳激波形成时间推迟,并且有变弱的趋势。另外,随着攻角的增加,伞内驻点上移,又伞前激波变弱,但是系统周围的脉动流场模式未变,并且伞内高压区仍然会出现周期性变化,所以伞绳激波在其推动下亦向上游传播,并与前体激波出现相互作用。需要注意的是,下面的伞绳激波与前体尾流、前体激波的相互作用区域基本稳定在伞体附近,没有出现较大的远离,随着前体激波/伞前激波的相互作用愈来越弱,该相互作用区域亦向下游流去直至消失。
(a)= 105/46 (b)=145/46 (c)=195/46
(d)= 215/46 (e)=245/46 (f)=275/46
(a)= 1510/46 (b)=1710/46 (c)=1810/46
(d)= 2110/46 (e)=2510/46 (f)=2810/46
3.2 伞内压力及阻力的影响
图6为伞内上下表面平均压力分布随着攻角的变化。图中,为距离伞面内中心的弧线距离;为伞内最大弧长;为静压;¥为来流压力。从图6可以发现,攻角=5°时,伞内上下面的压力分布最小,而攻角为=10°的压力反而有所上升,这说明,=0°和=5°时,脉动流场结构变化明显,伞内压力周期性变化幅值较大,所以伞内表面的时间平均压力分布未能达到最高;而=5°时,系统周围的气动干扰比=0°时减弱,所以压力有所下降。=10°时,脉动流场模式减弱,伞内压力周期性变化幅值较小,并且激波/激波,激波/尾流相互作用区域未远离降落伞系统,所以伞内压力分布最大,但是由于伞内高压驻点上移,使得伞内中心连接轴附近压力出现显著下降。

图6 伞内上下表面平均压力分布随着攻角的变化
流场的不稳定会导致伞衣的阻力出现不稳定状态,阻力作用在来流方向,其由伞体表面的内外压力差计算所得。然而,为了更精确的定义和比较,阻力系数被用来表征降落伞系统的性能。阻力系数d[7]定义如下:

式中是伞体表面的内外压差;动压由静压和来流马赫数计算:,这里。
图7为随着攻角的增加降落伞的平均阻力系数曲线。可以发现=0°下的计算结果(CFD)和试验结果(EXP,来自日本航空航天局)吻合较好,并且随着攻角的增加,阻力系数有明显上升。这说明随着攻角的增加,伞体背面的压力分布随着攻角的增加而出现不均匀,其使得伞体的内外压差升高,进而获得了较大的阻力。
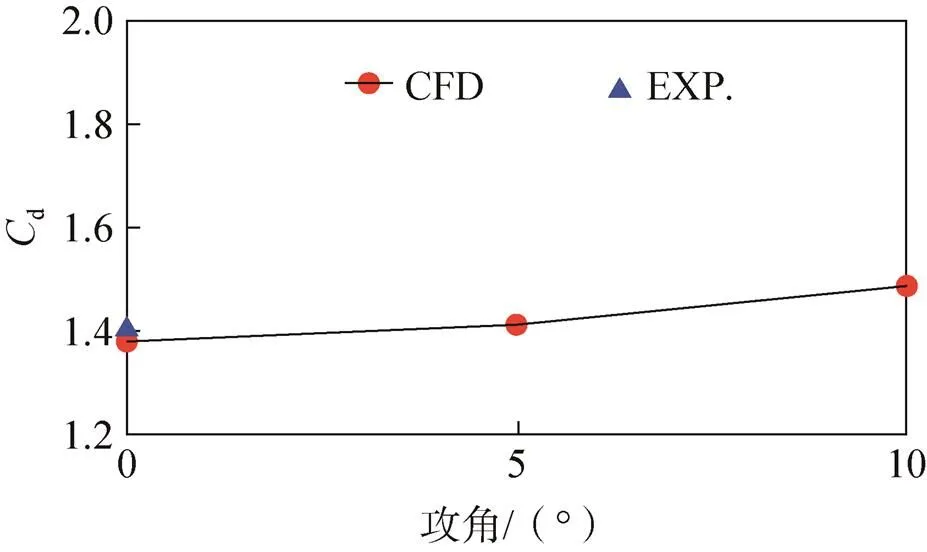
图7 不同攻角下的降落伞的平均阻力系数
4 结束语
本文主要分析了不同攻角下降落伞伞绳对于系统周围复杂流场结构以及降落伞性能表现的影响。结果表明,由于攻角的影响,非定常流场结构呈现上下不对称,并且上下伞绳激波形成时间不同步。上面的伞绳激波有一个由弱增强的过程,下面的伞绳激波处于稳定状态。当伞内高压而形成的伞前激波与伞绳激波相交时,伞绳激波开始脱离伞绳,向上游传播,最后形成周期性变化的脉动流场结构。随着攻角的增加,上下面的伞绳激波形成时间出现推迟,并且有变弱的趋势。另外,在=10°下,下面的伞绳激波与前体尾流、前体激波的相互作用区域基本稳定在伞体附近,没有出现较大的远离,这使得伞体内表面的压力出现升高。另外,由于攻角与伞绳的综合影响,伞内表面的时间平均压力分布在=5°时最小,而在=10°时最大,阻力系数却随着攻角的增加而出现了单调增加。
[1] SENGUPTA A, STELTZNER A. Results from the Mars Science Laboratory Parachute Decelerator System Supersonic Qualification Program[C]//Aerospace Conference, Big Sky, MT, USA. IEEE, 2008.
[2] STEINBERG S Y, SIEMERS III P M, SLAYMAN R G. Development of the Viking Parachute Configuration by Wind-tunnel Investigation[J]. Journal of Spacecraft, 1974, 11: 101-107.
[3] MAYBUE R J, BOBBITT P J. Drag Characteristics of a Disk-gap-band Parachute with a Nominal Diameter of 1.65 Meters at Mach Number from 2.0 to 3.0[R]. NASA Technical Note, NASA TN D-6894, 1972.
[4] HEINRICH H G. Aerodynamics of the Supersonic Guide Surface Parachute[J]. Journal of Aircraft, 1966, 3(2): 105-111.
[5] MOORMAN C J. Fluid-structure Interaction Modeling of the Orion Spacecraft Parachutes[D]. Texas: Master Thesis of Rice University, 2010.
[6] SENGUPTA A. Fluid Structure Interaction of Parachutes in Supersonic Planetary Entry[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 23-26 May 2011, Dublin, Ireland. AIAA Paper 2011-2541, 2011.
[7] SENGUPTA A, KELSCH R. Supersonic Performance of Disk-gap-band Parachutes Constrained to a 0-degree Trim Angle[J]. Journal of Spacecraft and Rockets, 2009, 46(6): 1155-1163.
[8] SENGUPTA A, STELZNER A. Findings from the Supersonic Qualification Program of the Mars Science Laboratory Parachute System[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 4-7 May 2009, Seattle, Washington. AIAA Paper 2009-2900, 2009.
[9] 陈猛, 王璐, 陈涵, 等. 降落伞充气过程流固耦合方法的数值预测分析[J]. 南京航空航天大学学报, 2013, 45(4): 515-520.CHEN Meng, WANG Lu, CHENG Han, et al. Numerical Prediction Analysis of Parachute Inflation Process Using Fluid-structure Interaction Method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(4): 515-520. (in Chinese)
[10] 薛晓鹏, 温志湧. 超声速降落伞系统的气动干扰数值模拟[J]. 航天返回与遥感, 2016, 37(3): 9-18. XUE Xiaopeng, WEN Chihyung. Numerical Simulation of Aerodynamic Interaction of Supersonic Parachute System[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(3): 9-18. (in Chinese)
[11] LINGARD J, DARLEY M, UNDERWOOD J C. Simulation of Mars Supersonic Parachute Performance and Dynamics[C]// 19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 21-24 May 2007, Williamsburg, VA. AIAA Paper 2007-2507, 2007.
[12] KARAGIOZIS K, KAMAKOTI R, CIRAK F, et al. A Computational Study of Supersonic Disk-gap-band Parachutes Using Large-eddy Simulation Coupled to a Structural Membrane[J]. Journal of fluids and Structures, 2011, 27(2): 175-192.
[13] XUE X, NAKAMURA Y. Numerical Simulation of a Three-dimensional Flexible Parachute System under Supersonic Conditions[J]. Trans. JSASS Aerospace Tech. Japan, 2013, 11: 99-108.
[14] GAO X, ZHANG Q, TANG Q. Numerical Modeling of Mars Supersonic Disk-gap-band Parachute Inflation[J]. Advances in Space Research, 2016, 57(11): 2259-2272.
[15] XUE X, KOYAMA H, NAKAMURA Y, et al. Effects of Suspension Line on Flow Field Around a Supersonic Parachute[J]. Aerospace Science and Technology, 2015, 43: 63-77.
[16] XUE X, NISHIYAMA Y, NAKAMURA Y, et al. Numerical Investigation of the Effect of Capsule Half-cone Angle on a Supersonic Parachute System[J]. Journal of Aerospace Engineering, 2016, 29(4): 1-6.
[17] XUE X, NISHIYAMA Y, NAKAMURA Y, et al. High-speed Unsteady Flows Past Two-body Configurations[J]. Chinese Journal of Aeronautics, 2017. (In Press)
[18] XUE X, NISHIYAMA Y, NAKAMURA Y, et al. Parametric Study on Aerodynamic Interaction of a Supersonic Parachute System[J]. AIAA Journal, 2015, 53(9): 2796-2801.
[19] XUE X, KOYAMA H, NAKAMURA Y. Numerical Simulation of Supersonic Aerodynamic Interaction of a Parachute System[J]. Trans. JSASS Aerospace Tech. Japan, 2013, 11: 33-42.
[20] NISHIYAMA Y. Aerodynamic Characteristics of the Supersonic Parachute with its Opening Process[D]. Nagoya: Master thesis of Nagoya University, 2013.
[21] SHIMA E, JOUNOUCHI T. Roe of CFD in Aeronautical Engineering (No.14) -AUSM Type Upwind Schemes: Proceedings of 14th NAL Symposium on Aircraft Computational Aerodynamics[C]. Japan: Special Publication of National Aerospace Laboratory, NAL-SP-34, 1997: 7-12.
[22] BENNEY R J, STEIN K R. Computation Fluid-structure Interaction Model for Parachute Inflation[J]. Journal of Aircraft, 1996, 33(4): 730-736.
[23] MIYOSHI M, ISHII T, HASHIMOTO A, et al. Computational Analysis of Parachute Motion Using the Immersed Boundary Method[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, 7-10 January 2008, Reno, Nevada. AIAA Paper 2008-311, 2008.
(编辑:陈艳霞)
Effects of Suspension Lines on the Supersonic Parachute System at Different Angles of Attack
XUE Xiaopeng1WEN Chihyung2WANG Yunpeng3ZHANG Deliang3
(1 School of Aeronautics and Astronautics, Central South University, Changsha 410083, China)(2 Shenzhen Research Institute, The Hong Kong Polytechnic University, Shenzhen 518057, China)(3 The State Key Laboratory of High Temperature Gasdynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China)
In the present study, a three-dimensional parachute system in supersonic flow is numerically simulated using a simple “immersed boundary technique” together with the fluid-structure coupling scheme. The parachute system employed here consists of a capsule and a canopy, where the suspension lines are applied to connect them. The objective of this study is to investigate the effects of suspension lines on the complex unsteady flow structures around the parachute system, and the performance of the supersonic parachute at different angles of attack. As a result, since the distance between the capsule and canopy is rather small, the aerodynamic interactions around the parachute system exhibit more apparent asymmetric flow/shock features when the angle of attack increases, and the suspension line shocks on the upper/lower surfaces are formed at different time. As the angle of attack is increased, the suspension line shocks are postponed to form, and become weaker. In addition, because of the coupling effects of the angle of attack and suspension line shocks, the time-averaged pressure distribution on the canopy inner surface becomes smallest at 5 degree of angle of attack, and reaches to be greatest at 10 degree; however, the drag coefficient increases with the angle of attack increment.
supersonic parachute; suspension line; angle of attack; numerical simulation; Landing
V445
A
1009-8518(2017)04-0047-08
10.3969/j.issn.1009-8518.2017.04.006
薛晓鹏,男,1982年生,2013年获日本名古屋大学航空航天工程专业博士学位,讲师。研究方向为气动力减速器技术数值计算方法。E-mail:xuexiaopeng@csu.edu.cn。
温志湧,男,1964年生,1994年获美国加州理工学院航天博士学位,教授。研究方向包括高超空气动力学、实验流体力学、智能流体。
汪运鹏,男,1978年生,2012年获日本名古屋大学航空航天工程专业博士学位,副研究员。研究方向为风洞试验方法与气动力精确测量技术。
张德良,男,1939年生,1964年毕业于中国科学技术大学近代力学系,研究员。研究方向为计算流体动力学和数值方法研究、高超声速空气动力学、计算力学及应用。
2016-12-19

