基于离散元方法的月球着陆器冲击月壤过程分析
梁绍敏 王永滨 季顺迎
基于离散元方法的月球着陆器冲击月壤过程分析
梁绍敏1王永滨2季顺迎1
(1 大连理工大学工业装备结构分析国家重点实验室,大连116023)(2 北京空间机电研究所,北京100094)
月球着陆器在着陆过程中会产生巨大的冲击作用。为了研究月壤材料对着陆器的缓冲作用,文章针对月壤在细观尺度下的离散分布特性,采用离散元方法建立月壤的计算分析模型。在此基础上,简化着陆器模型仅考虑着陆腿的缓冲性能,对着陆过程中着陆器与月壤相互作用的动力冲击过程进行数值分析。通过调整着陆器的质量以及着陆速度,对着陆器着陆过程中的冲击深度、加速度以及冲击力进行了计算分析,研究了月壤对着陆器的缓冲性能。计算结果表明,月壤材料对着陆器有很好的缓冲作用,这为实现安全稳定的软着陆提供了新的研究方向。采用离散元方法分析着陆器在着陆冲击过程中冲击力的变化规律有助于着陆器结构的合理设计和安全性能评估。
缓冲性能 离散元方法 冲击载荷 月壤 月球着陆器
0 引言
月球着陆器在着陆过程中会产生巨大的冲击,这对探测设备和登月人员的安全形成严重威胁。为保证内部精密仪器的完备性,实现着陆器的安全软着陆,对其着陆过程的冲击力及各缓冲装置的研究至关重要[1-2]。着陆器自身具有一定的缓冲设备,在着陆过程中通过自身的缓冲设备来减缓着陆器受到的冲击[3-4]。现有研究主要关注着陆器自身的缓冲功能:气囊缓冲器结构简单、缓冲性能好,但其容易产生反弹和翻滚且不易控制[5];弹簧棘轮缓冲器具有空间适应能力强、结构简单且能够着陆姿态自修复等优点,但其稳定性差且不易控制[6-7];文献[8]对着陆器的铝蜂窝、金属橡胶、涡流磁阻尼等缓冲材料进行高低温冲击试验并对缓冲器的着陆性能进行分析。至此,国内外的研究主要围绕着陆器自身的缓冲设施,对月面做刚性假设,并且大多研究基于有限元原理[9]。这显然忽视了月壤这种颗粒材料在着陆器着陆过程中所起的重要作用。
颗粒材料因其特殊的存在形式而有特殊的物理性质,如它兼有流体和固体的性质,并在一定条件下可发生类固液相变[10]。颗粒材料还具有快速耗能的特性从而具有缓冲的作用,这在现实生活中得到了广泛地应用。当颗粒材料受到外界载荷的作用时,颗粒之间产生强烈的挤压和碰撞,从而吸收冲击物的能量,使系统的能量得到快速有效的衰减。因此颗粒材料常被用来作为降噪、吸能减震和缓冲的优选材 料[11]。探月测试着陆器在着陆过程中,月壤的颗粒材料对缓冲,对实现平缓、顺利的软着陆起到很重要的作用。
人们对月壤性质的研究最早是通过天文望远镜观测月球表面,将其结果与地面物质作对比;随着人类对月球探测活动的发展,通过探测器携带回来累计约382.0kg的月壤返回地球,这给之后的月壤研究提供了宝贵的资料[12]。但由于月壤数量有限,不能满足学者的研究需求,因此模拟月壤顺势而生并获得了很多研究成果。然而对模拟月壤的研究大多是通过试验的方法,应用数值模拟则相对较晚,且研究技术不成熟,总体来说主要是通过有限元的方法建立月壤整体的连续模型和离散元的方法建立月壤材料的离散模型[13]。采用有限元方法的研究有通过ABAQUS建立了月壤模型,对均布静荷载作用下月壤的变形进行了分析;利用DYTRAN以典型月壤为参考建立模型,对月壤动力特性进行了模拟研究;文献[14]基于ADAMS建立了月壤模型对着陆过程进行了仿真,研究了着陆器着陆过程的稳定性[14]。然而受所建月壤模型连续性的影响,其研究结果存在一定的缺陷[15]。通过离散元方法研究月壤材料是将月壤看作离散颗粒的集合体,根据其离散特性,将每个月壤颗粒作为一个单元建立模型,进行模拟计算,可以充分考虑月壤颗粒本身的物理特性,尤其是在缓冲方面,能够实现颗粒之间力的传播分析,从而更加有效地模拟着陆器在着陆过程中月壤颗粒的缓冲吸能。因此在分析具有离散特性的月壤材料方面,离散元方法具有很大的优势[16-17]。
本文建立了月壤材料的离散元模型,并以月壤为主要研究对象,在未考虑着陆器自身铝蜂窝缓冲的吸能效果的情况下,通过离散元方法模拟着陆器在着陆过程中与月壤相互作用的过程。改变着陆器的着陆速度、着陆器质量,分析着陆器足垫(着陆腿底部与着陆面接触的部分)的冲击深度、冲击过程中加速度的变化以及冲击力的大小等,研究月壤对着陆器的缓冲作用。同时还与全尺寸着陆冲击试验结果做了对比,以验证本模拟结果的正确性。为着陆器结构的设计提供科学依据,为实现安全着陆提供理论基础。
1 着陆缓冲系统及月壤的离散元模型
为模拟月球着陆器着陆冲击过程,依据现有着陆器的实际结构建立着陆器缓冲系统的模型,并通过离散单元法建立月壤材料的离散元模型。通过分析颗粒之间的相互作用力,以及在冲击过程中的能量变化,可从细观尺度分析着陆器的冲击过程。
1.1 着陆器缓冲系统结构模型
着陆器的结构模型有很多种,包括阿波罗月球着陆器、欧空局月球着陆器、哈工大月球着陆器以及北京空间机电研究所月球着陆器等。这些着陆器主要以腿式结构为主,如图1所示。由于目前对腿式着陆器研究较多且技术相对成熟,因此本文对腿式着陆器的着陆过程进行计算分析,并根据图2所示广泛采用的着陆器结构建立简化的四腿着陆器结构模型,并将结构质量均匀分布于各节点处。主要计算参数列于表1中。

图1 国内外主要的腿式月球着陆器
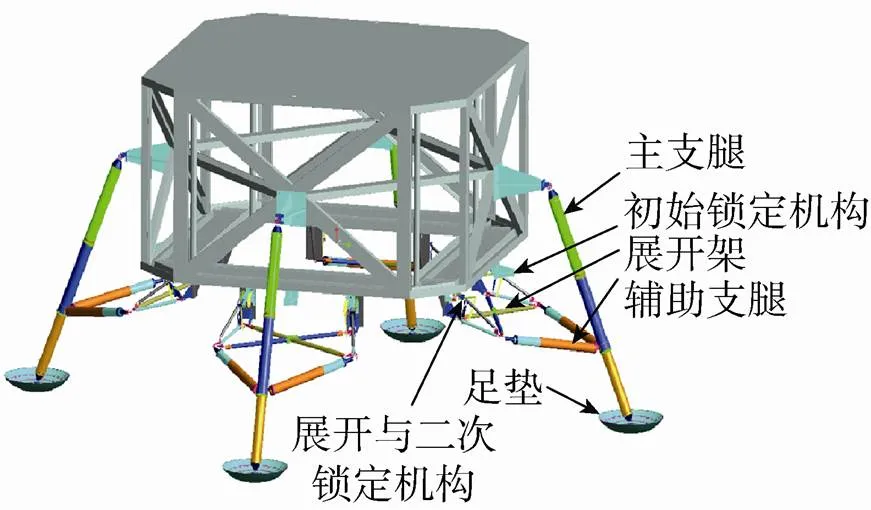
(a)展开状态 (b)收拢状态
表1 着陆器结构与物理参数

Tab.1 Lander structure and physical parameters
1.2 月壤离散元模型
针对月壤材料的离散分布特性,可采用离散元方法对其动力过程进行数值分析。月壤颗粒间的作用力可基于球形单元的非线性接触模型进行计算。颗粒间的接触力包括弹性力、粘滞力以及基于Mohr-Coulomb准则的滑动摩擦力[18]。本文采用Hertz-Mindlin非线性接触模型。颗粒之间的法向接触力包括Hertz弹性力和非线性粘滞力,即
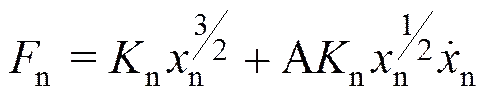
式中n为法向刚度系数;n和分别为颗粒法向重叠量及该方向的相对速度;A为颗粒间的粘滞参数,是由变性参数、粘滞参数和泊松比等参数决定的,可以通过颗粒碰撞过程中的回弹系数来确定。
基于Mindlin理论和Mohr-Coulomb摩擦定律,忽略粘滞力的影响,则颗粒间切向接触力s为:
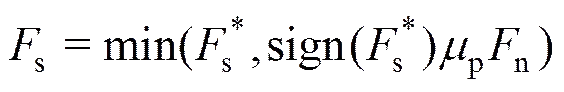
(3)
式中s为切向刚度系数;s为颗粒的切向变形量;p为颗粒表面摩擦系数。本文采用的法向刚度n和切向刚度s分别取为:
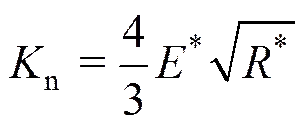
(5)
着陆器在着陆过程中垂直方向的能量h为
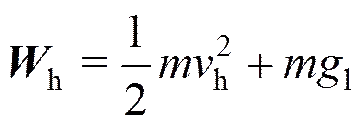
式中为着陆器的总质量;h为垂直着陆速度;1为月球表面重力加速度;∆为着陆器着陆缓冲过程中质心下降高度。
着陆舱着陆过程中的水平方向能量v为
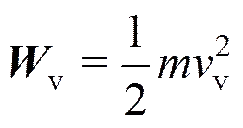
式中ν为水平着陆速度。
着陆器本身具有缓冲作用,即着陆器自身配有缓冲装置。设在着陆过程中,该装置在垂直方向的能量吸收功为h,在水平方向的能量吸收功为v。令月壤颗粒系统在缓冲过程中垂直和水平方向吸收的能量分别是h、v。当着陆器的速度降为零时冲击过程结束,整个过程能量守恒,即
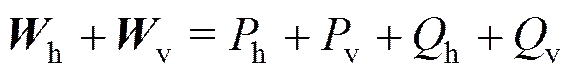
根据月壤的物理性质,以球形颗粒模拟月壤颗粒,并采用非规则排列方式建立月壤材料的离散元模型,如图3所示,相关计算参数列于表2中[12,20]。月壤在与着陆器接触过程中,通过颗粒与颗粒之间的相互作用来快速吸收着陆器的能量,从而起到缓冲的作用。
表2 月壤计算模型参数
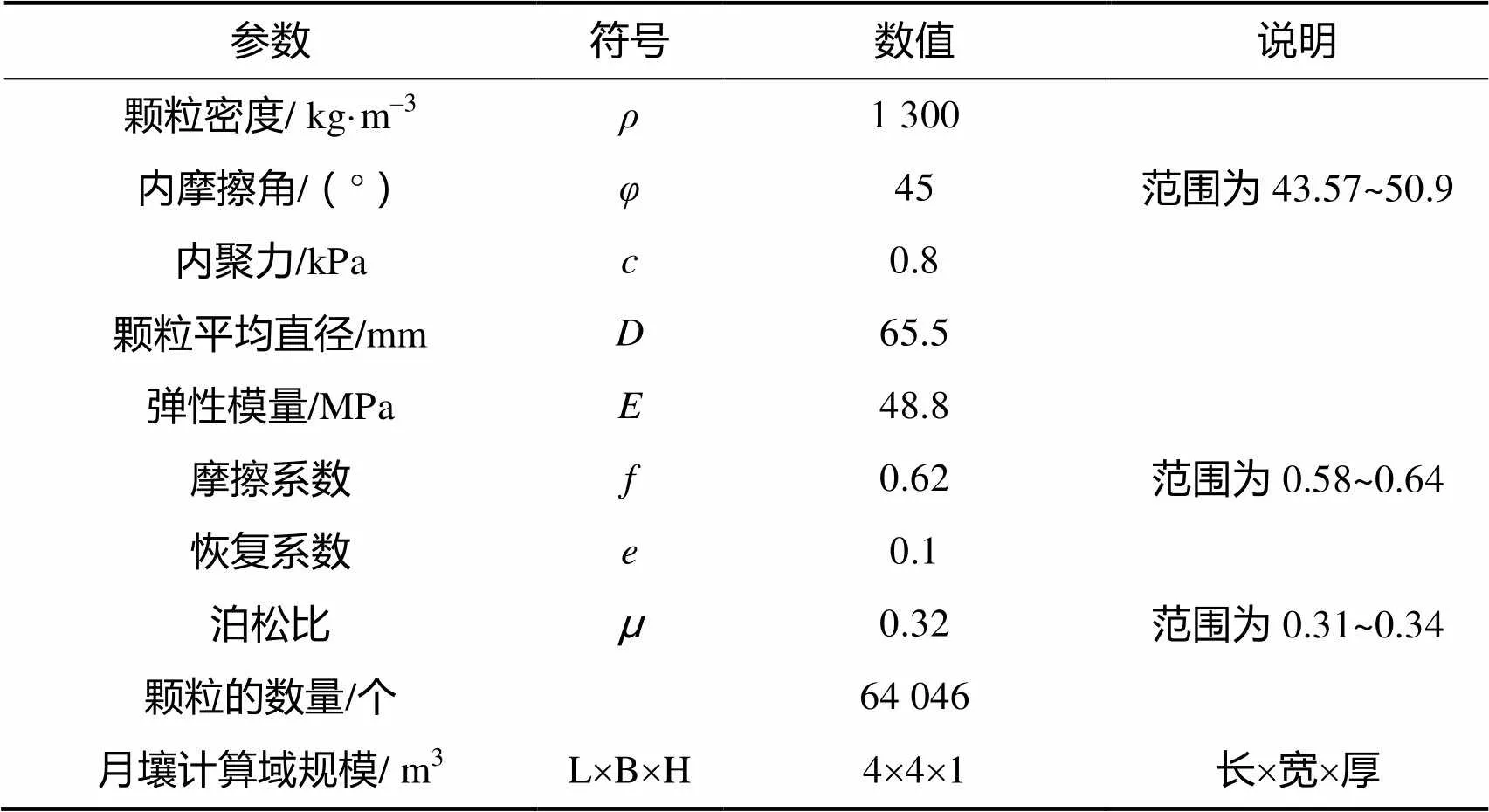
Tab.2 The parameters of the lunar soil model

图3 月壤的离散元模型
2 着陆过程的离散元分析和冲击力特性
着陆器以一定的速度冲击月壤表面,在与月壤接触过程中,颗粒之间通过相互碰撞挤压起到缓冲的作用,最终着陆器的速度降为零,着陆过程结束。文献[21]等进行的全尺寸着陆冲击试验获得载人登月舱最大过载发生在无水平速度和坡度的工况,最大过载为3.97。文献[21]通过仿真分析,在不考虑月壤颗粒缓冲性能的情况下,获得着陆舱体着陆冲击过载介于1.50~3.40之间,着陆器本身着陆冲击过载小于4.00(该值为载人登月舱所能承受的最大过载)。本研究所得着陆器冲击过载为2.20~3.11之间。
2.1 着陆器在月壤着陆过程的冲击力分析
着陆器着陆过程可简化为垂直冲击和水平滑行两个过程的组合。本文重点研究垂直冲击过程着陆器首先着陆部分即足垫与月壤之间的相互作用。在两者接触瞬间存在着动量和能量的传递。具体模拟过程如图4所示。在数值模拟过程中,通过改变着陆器质量以及着陆器的着陆速度,观察着陆器着陆过程浸入月壤的深度、着陆器加速度的变化过程以及月壤受到的冲击力,并分析其变化规律。

图4 着陆器的着陆冲击过程
着陆器在着陆过程中主要经历3个阶段:(1)足垫和月壤接触后的冲击阶段;(2)足垫在月壤中的滑行阶段;(3)平衡稳定阶段[20]。由于滑行阶段主要是水平方向的运动,对月壤模型的规模要求很大,这将大大影响模拟过程的计算效率;此外本文重点研究冲击过程,即着陆器在竖直方向的运动,因此本文主要研究第一和第三个阶段。图5为足垫与月壤材料接触后各阶段的运动状态,其中颗粒不同的颜色表示所受到不同的法向力,由紫色到红色表示法向力由小到大。冲击力的大小直接影响软着陆的动力过程。在着陆器着陆过程中,竖直方向所受力的时程曲线如图6所示。图6表明在与颗粒刚接触时着陆器受到的力最大,且在此接触过程中着陆器将动能传递给月壤材料,通过月壤颗粒与着陆器以及颗粒之间的相互作用,降低着陆器的能量,达到缓冲的效果。图7给出了在整个着陆过程中着陆器速度的变化情况,着陆器的速度在开始较大,受到的力也较大,因此加速度较大,即着陆器的速度在开始阶段变化很快,之后有较小的波动,最终速度降为0,着陆器达到稳定状态。
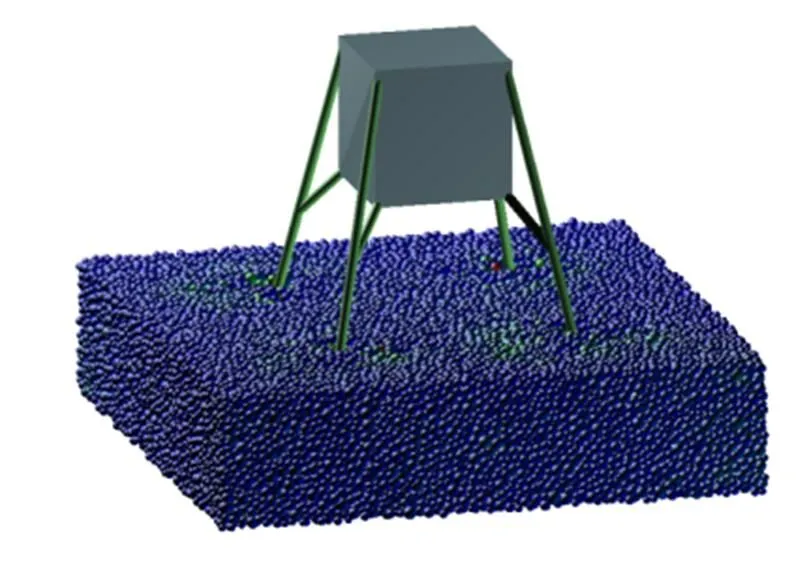
(a)开始接触 (b)冲击过程
(a)Start contact (b)Impact process
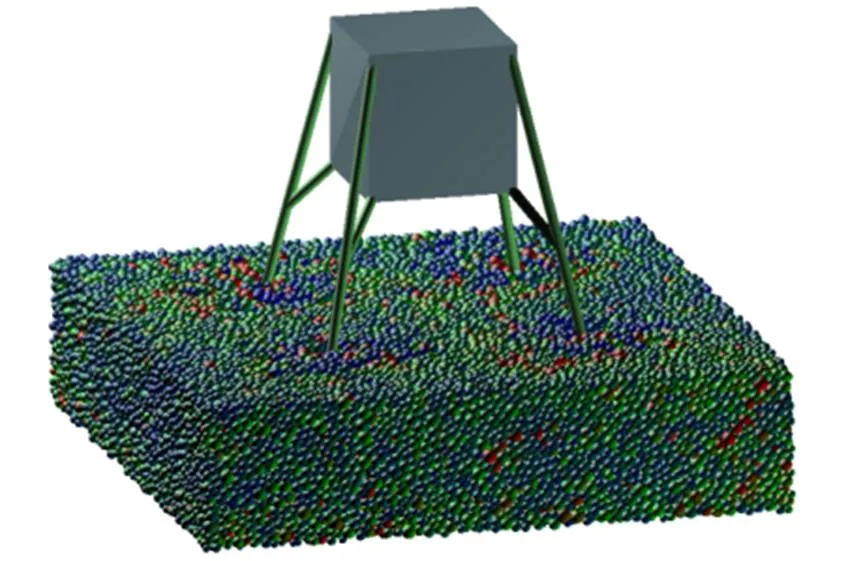
(c)完全浸入 (d)稳定阶段
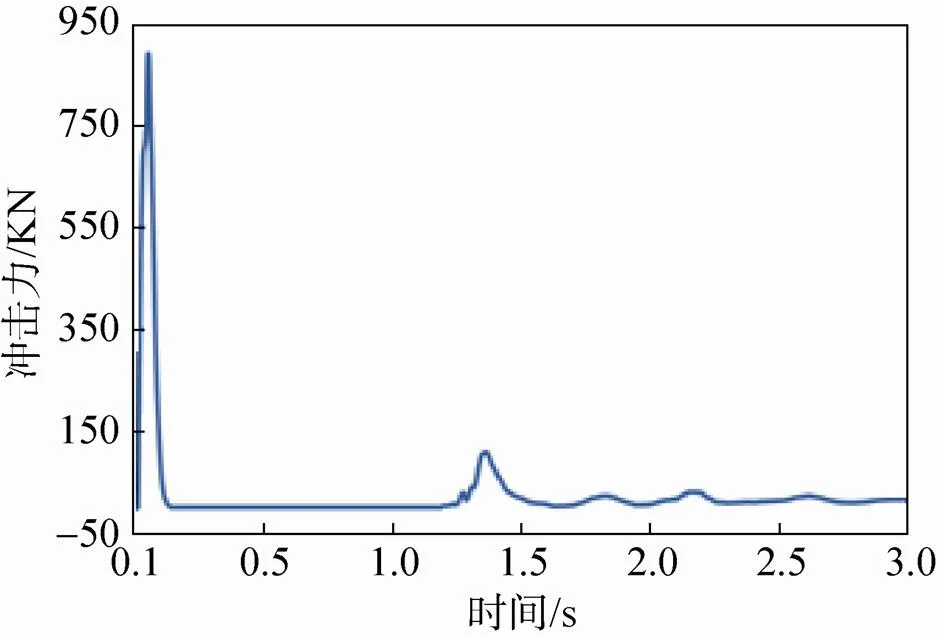
图6 着陆器在着陆过程中竖直方向所受力的时程
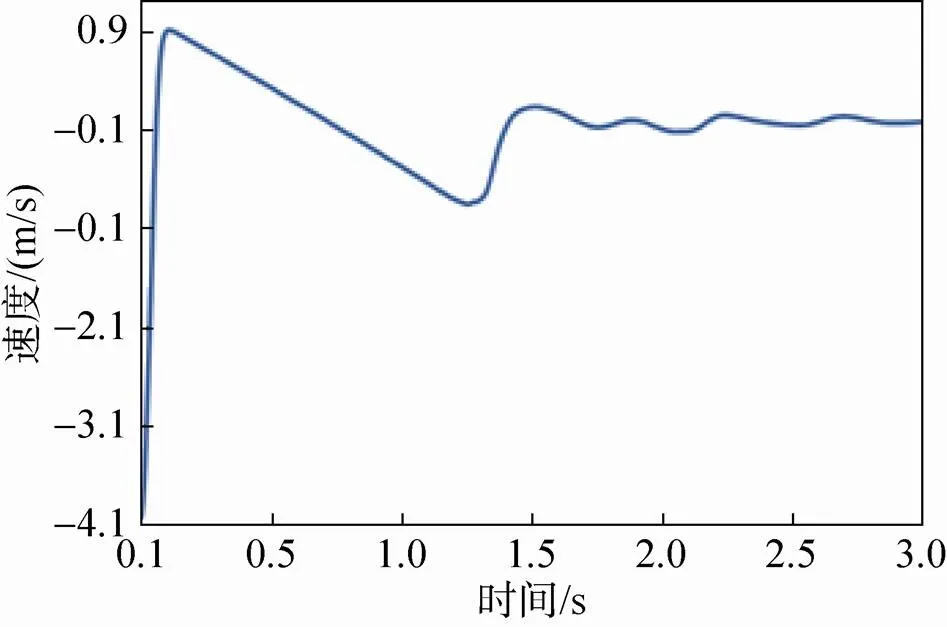
图7 着陆器在着陆过程中速度的时程
2.2 冲击速度对缓冲性能的影响
通过以上分析发现,影响着陆效果的因素之一是垂直冲击速度,其对月壤的缓冲效果具有关键作用。研究过程中取着陆速度为2m/s、2.5m/s、3m/s、3.5m/s、4m/s、4.5m/s、5m/s、6m/s,着陆器质量取9 000kg。着陆器在着陆过程中受到的冲击力峰值变化规律如图8所示,该图表明冲击力峰值随冲击速度的增大线性增大,即冲击速度越大冲击力峰值越大。观察着陆器冲击过程中的加速度峰值变化,其结果如图9所示。从图中可以看出改变着陆速度,着陆器冲击过程中的加速度峰值随之增加,且趋于线性关系。图10为冲击深度与冲击速度的关系,随着冲击速度的增大,着陆器的动能增大,在冲击过程中将会达到更大的深度,即竖向位移会随之增大。本文计算了在冲击过程中月壤材料吸收的能量,其规律如图11所示,冲击速度越大着陆器与颗粒接触的时间越长,颗粒吸收的能量也就越大,但其变化趋势并非线性的,而是在速度较小时变化较慢,当速度较大时颗粒吸收的能量变化较快。
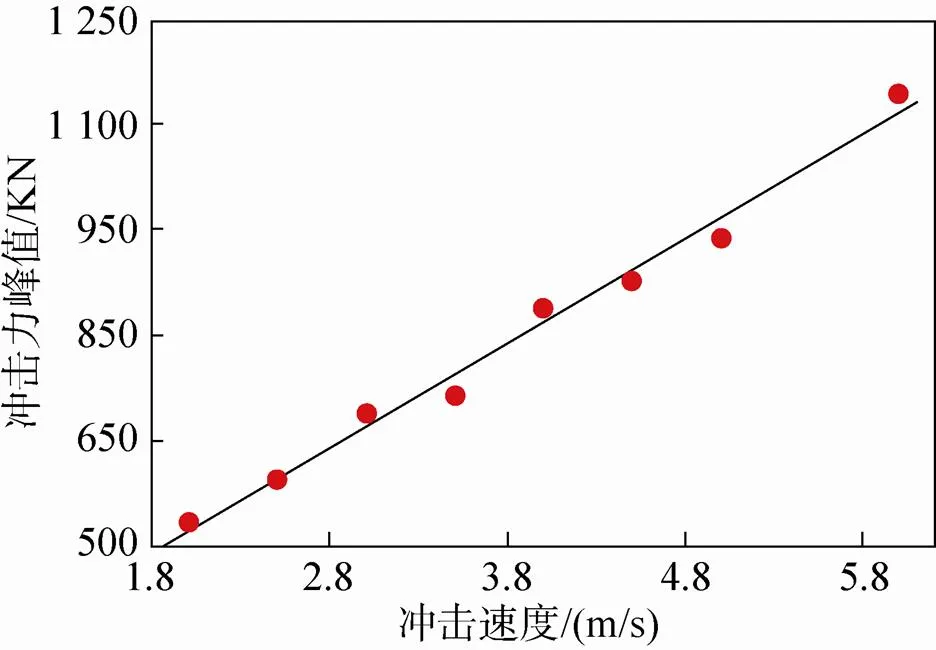
图8 冲击力峰值与冲击速度的关系
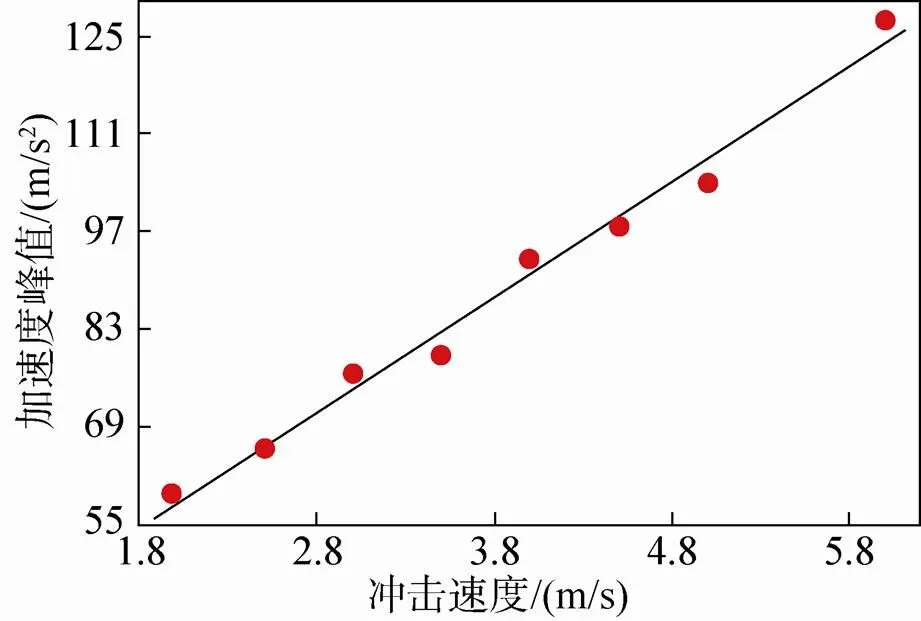
图9 加速度峰值与冲击速度的关系
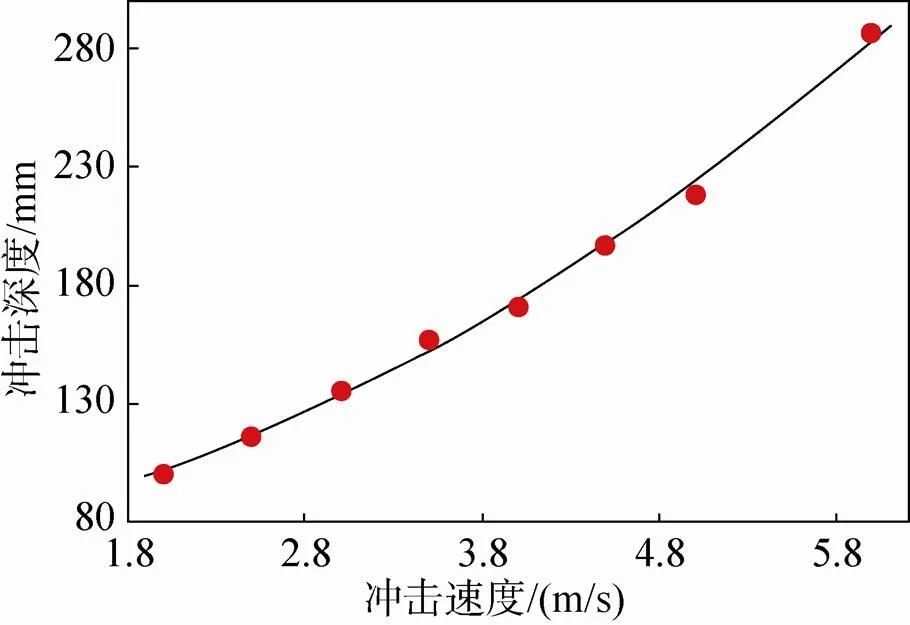
图10 冲击深度与冲击速度的关系
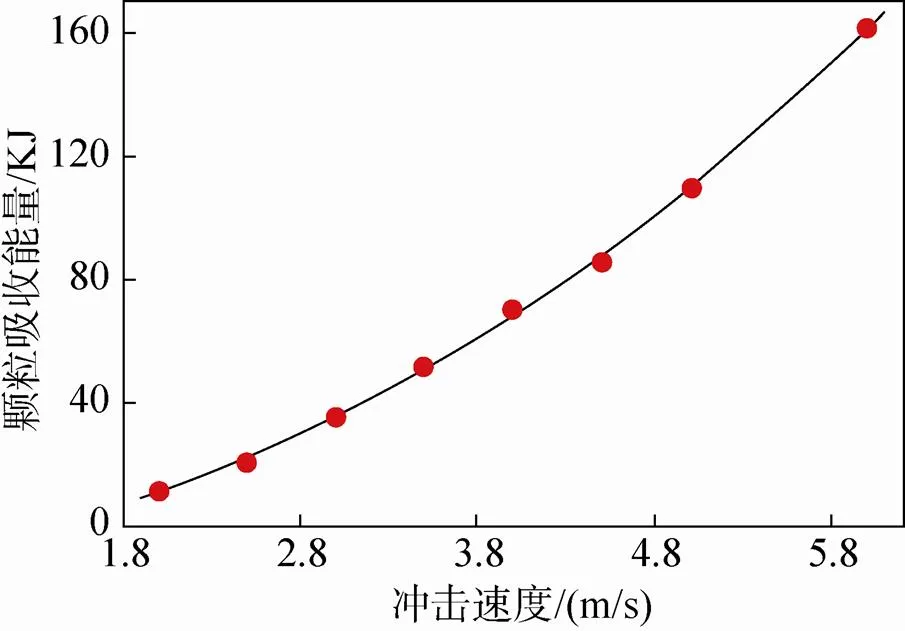
图11 颗粒吸收能量与冲击速度的关系
对冲击速度的研究对着陆器的着陆过程具有指导作用,同时也充分说明了冲击速度是影响着陆过程的重要因素。
2.3 着陆器质量对缓冲性能的影响
通过对着陆器垂直冲击模拟实验的研究,着陆器的冲击深度、冲击力峰值和加速度主要受冲击速度、土体密实度和着陆器质量的影响[20]。本文参考实际着陆器质量9 000kg,并在此基础上调节其质量为 7 000kg、7 500kg、8 000kg、8 500kg、9 000kg、9 500kg,研究质量对缓冲性能的影响规律,研究过程中冲击速度为4m/s。改变着陆器的质量研究着陆器所受冲击力峰值的变化规律如图12所示,显然冲击力峰值随着陆器质量的增大而增大。图13为加速度峰值随着陆器质量的变化过程。从图中可以看出,在着陆器质量较小时加速度的峰值变化较快,当质量达到8 500kg时,加速度峰值的增加速度趋于平缓。此外本文也研究了冲击深度与质量的关系,如图14所示。从图中可以看出冲击速度与质量的线性关系非常突出。通过计算我们也获得了颗粒吸收的能量随质量的变化如图15,其规律也近于线性关系。
无论是改变冲击速度还是改变着陆器的质量,实质是在改变冲击能。由以上结果可得出结论,冲击力峰值随冲击能的增大而增大。
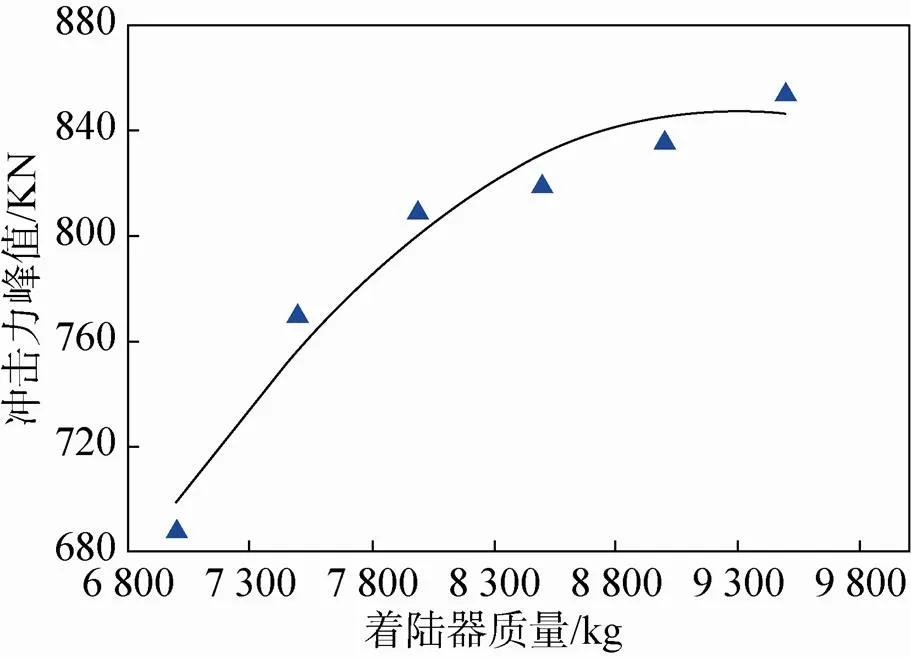
图12 冲击力峰值与着陆器质量的关系
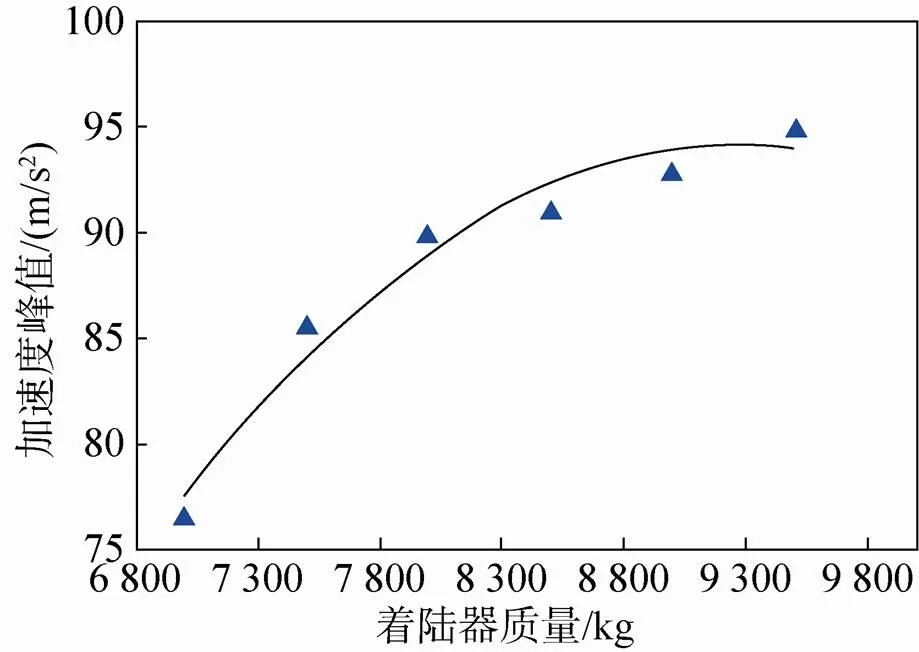
图13 着陆器质量对着陆器加速度的影响

图14 冲击深度与着陆器质量的关系
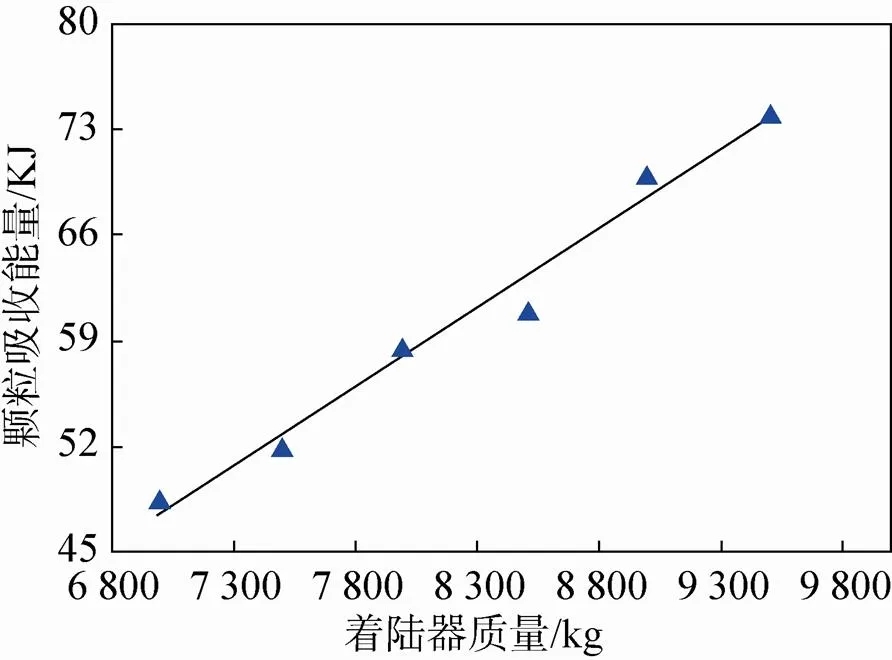
图15 颗粒吸收能量与着陆器质量的关系
3 结论
本文建立了着陆器结构模型,以及月壤材料的离散元模型,通过离散元方法研究着陆器在着陆过程中与月壤相互作用的过程,分析月壤对着陆器缓冲性能的影响因素及变化规律。计算结果表明,影响着陆器冲击深度、冲击力峰值和加速度峰值的主要因素有着陆器质量和冲击速度等,在着陆器的结构研究和着陆的技术研究中,需要重点考虑这些因素并做深入的分析;着陆器在与颗粒接触瞬间冲击力最大,随后迅速减小,这正是颗粒缓冲作用的重要体现;冲击深度、冲击力峰值和加速度峰值均随冲击速度和着陆器质量的增大而增大,变化规律相似;冲击速度和着陆器质量两个因素对冲击过程的影响实质是冲击能的影响。研究表明,冲击能越大冲击深度越大,且趋于线性关系;冲击能越大加速度峰值越大,且变化趋势先急促后平缓;冲击能越大颗粒吸收的能量越多,且近于线性关系。
在后续工作中,将完善着陆器模型的构建,继续研究影响月壤材料缓冲作用的其他因素及其规律;设计并完成着陆器对月壤材料的冲击试验,并将其结果与模拟结果对比,验证模拟结果的正确性。
[1] 朱汪. 欧洲航天局月球着陆器概述及启示[J]. 航天器工程, 2016, 25(1): 124-130. ZHU Wang. Overview and Enlightenment of ESA Lunar Lander[J]. Spacecraft Engineering, 2016, 25(1): 124-130. (in Chinese)
[2] TANG X H, QIAN L F, SHI H J. Chassis Strength Analysis of Vehicle-mounted Gun for Heavy Cargo Airdrop during Soft Landing Buffer[J]. Journal of Gun Launch & Control, 2014, 35(1): 35-39.
[3] LI F, YE M, YAN J, et al. A Simulation of the Four-way Lunar Lander-orbiter Tracking Mode for the Chang’E-5 Mission[J]. Advances in Space Research, 2016, 57(11): 2376-2384.
[4] 杨建中, 曾福明, 满剑锋, 等. 嫦娥三号着陆器着陆缓冲系统设计与验证[J]. 中国科学:技术科学, 2014(5): 440-449. YANG Jianzhong, ZENG Fuming, MAN Jianfeng, et al. Design and Verification of Chang'e III Lander Landing Buffer System[J]. Science China: Technological Sciences, 2014(5): 440-449. (in Chinese)
[5] HE H, CHEN Z, HE C, et al. A Hierarchical Updating Method for Finite Element Model of Airbag Buffer System under Landing Impact [J]. Chinese Journal of Aeronautics, 2015, 28(6): 1629-1639.
[6] 陈金宝, 聂宏, 赵金才, 等. 月球探测器软着陆缓冲机构着陆性能分析[J]. 宇航学报, 2008, 29(6): 1729-1732. CHEN Jinbao, NIE Hong, ZHAO Jincai, et al. Land Performance Analysis of Lunar Probe Soft Landing Buffer Mechanism[J]. Journal of Astronautics, 2008, 29(6): 1729-1732. (in Chinese)
[7] CHEN J B, NIE H, ZHAO J C. Review of the Development of Soft-landing Buffer for Lunar Explorations[J]. Journal of Astronautics, 2008, 29(3): 731-735.
[8] WANG S C, DENG Z Q, GAO H B, et al. Design of Impact Isolating Landing Legs for Micro-miniature Lunar Lander[J]. Journal of Harbin Institute of Technology, 2004, 36(2): 180-182.
[9] 丁建中, 王春洁, 王家俊, 等. 着陆工况对月球着陆器着陆缓冲性能影响分析[J]. 载人航天, 2016, 22(1): 132-137. DING Jianzhong, WANG Chunjie, WANG Jiajun, et al. Effect of Landing Condition on Lunar Lander Landing Buffer Performance [J]. Manned Space Flight, 2016, 22(1): 132-137. (in Chinese)
[10] FORTERRE Y, POULIQUEN O. Flows of Dense Granular Media[J]. Annual Review of Fluid Mechanics, 2008, 40(1): 1-24.
[11] SAKAMURA Y, KOMAKI H. Numerical Simulations of Shock-induced Load Transfer Processes in Granular Media Using the Discrete Element Method[J]. Shock Waves, 2011, 22(1): 57-68.
[12] GAO Y, SPITERI C, LI C L, et al. Lunar Soil Strength Estimation Based on Chang’E-3 Images[J]. Advances in Space Research, 2016, 58(9):1893-1899.
[13] JIANG M, SHEN Z, THORNTON C. Microscopic Contact Model of Lunar Regolith for High Efficiency Discrete Element Analyses[J]. Computers & Geotechnics, 2013, 54(10): 104-116.
[14] 蒋万松, 黄伟, 沈祖炜. 月球探测器软着陆动力学仿真[J]. 宇航学报, 2011, 32(3): 462-469. JIANG Wansong, HUANG Wei, SHEN Zuwei. Soft Landing Dynamics Simulation for Lunar Explorer[J]. Journal of Astronautics, 2011, 32(3): 462-469. (in Chinese)
[15] ARSLANTAS Y E, OEHLSCHLAGEL T, SAGLIANO M, et al. Safe Landing Area Determination for a Moon Lander by Reachability Analysis[J]. Acta Astronautica, 2016, 128: 607-615.
[16] 陆鑫, 黄勇, 李雯. 着陆作用下月尘激扬的三维离散元分析[J]. 航天器工程, 2011, 20(1): 101-108. LU Xin, HUANG Yong, LI Wei. Analysis the Excitability of Moon Particles in Landing Used Three-dimensional Discrete Element Method[J]. Spacecraft Engineering, 2011, 20(1): 101-108. (in Chinese)
[17] JIANG M, YIN Z Y, SHEN Z. Shear Band Formation in Lunar Regolith by Discrete Element Analyses[J]. Granular Matter, 2016, 18(2): 1-14.
[18] 季顺迎, 樊利芳, 梁绍敏. 基于离散元方法的颗粒材料缓冲性能及影响因素分析[J]. 物理学报, 2016, 65(10): 164-176. JI Shunying, FAN Lifang, LIANG Shaomin. Analysis of Cushioning Performance and Influencing Factors of Granular Materials Based on Discrete Element Method[J]. Acta Physica Sin1ica, 2016, 65(10): 164-176. (in Chinese)
[19] 孙其诚. 颗粒物质力学导论[M]. 科学出版社, 2009: 15-19. SUN Qicheng. Introduction to Particle Mechanics[M]. Science Press, 2009: 15-19. (in Chinese)
[20] 吴晓君, 钟世英, 凌道盛, 等. 着陆器足垫垂直冲击模型试验研究[J]. 岩土力学, 2012, 33(4): 1045-1050. WU Xiaojun, ZHONG Shiying, LING Daosheng, et al. Study on Vertical Shock Model Test of Lander Footpad[J]. Rock and Soil Mechanics, 2012, 33(4): 1045-1050. (in Chinese)
[21] 王永滨, 蒋万松, 王磊, 等. 载人登月舱月面着陆缓冲装置设计与研制[J]. 深空探测学报, 2016, 3(3): 262-267.WANG Yongbin, JIANG Wansong, WANG Lei, et al. Design and Development of Landing Gear Technology for Manned Lunar Landing[J]. Journal of Deep Space Exploration, 2016, 3(3): 262-267. (in Chinese)
(编辑:刘颖)
Analysis of Landing Impact Process of Lunar Landing Lander Based on Discrete Element Method
LIANG Shaomin1WANG Yongbin2JI Shunying1
(1 State Laboratory of Structural Analysis for Industrial Equipment Dalian University of Technology, Dalian 116023, China)(2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
The interaction between lunar lander and soil is of great importance due to the strong impact produced during the brief period of the space lander touchdown.In order to study the buffering effect of lunar soil material during lunar lander's soft landing process, this paper uses the discrete element method to establish the calculation model of lunar soil in view of the discrete distribution characteristics of lunar soil at the meso scale. Based on this, the lander model is simplified as a rigid body, and only the buffering performance of the landing legsis considered. The dynamic impact process of the landing is analyzed and the numerical simulation is carried out. By adjusting the quality and landing speed of the lander, the depth, acceleration and impact force of the lander are calculated and analyzed. The calculated results show that the lunar soil particles have a good buffering effect on the lander, which provides a new research direction for realizing security and stability of a soft landing. Using discrete element method to analyze the changes of impact force during the landing process, is helpful to the rational design and safety performance evaluation of the land structure.
buffering performance; discrete element method (DEM); impact load; lunar soil; lander
V476.3
A
1009-8518(2017)04-0055-09
10.3969/j.issn.1009-8518.2017.04.007
梁绍敏,女,1990年生,现在大连理工大学计算力学专业攻读硕士学位。研究方向为颗粒材料的缓冲性能、基于离散元方法的数值模拟、月球着陆器着陆过程的研究。E-mail:shaominliang@ mail.dlut.edu.cn。
2016-11-23
国家自然科学基金项目(11572067,51505028);中央高校基本科研业务费专项资金(DUT15ZD105)资助

